Basic Concepts of Motion
- Motion – An object is said to be in motion if its position changes with time.
- Rest – When an object does not change its position with time, it is said to be at rest.
- Reference Frame – The coordinate system used to describe motion.
- Motion is always relative to some reference frame.
Position, Distance and Displacement
- Position (x): The location of a particle on a coordinate axis at any instant.
- Path length (distance): The total length of the actual path travelled (scalar).
- Displacement (Δx): The change in position of a particle in a particular direction.
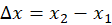
- Important Points:
- Distance ≥ |Displacement|
- If object returns to the starting point → Displacement = 0 but Distance ≠ 0.
Speed and Velocity
Speed
- Rate of change of distance.
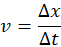
- Scalar quantity.
- Average Speed:
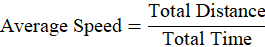
- If different speeds for equal distances:
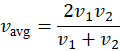
(Harmonic mean)
Velocity
- Rate of change of displacement.
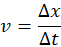
- Vector quantity (for 1-D, direction is shown by + or – sign).
Instantaneous Velocity
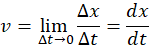
Average Velocity
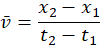
Relation between Speed and Velocity
- If direction of motion doesn’t change → Speed = |Velocity|
- If direction changes → Average speed > |Average velocity|
Also Read: Average Speed And Average Velocity
Acceleration
- Rate of change of velocity.
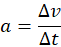
- Instantaneous acceleration:
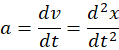
- Units: m/s²
- Positive acceleration: Speed increasing
- Negative acceleration (retardation): Speed decreasing
Equations of Motion (for Constant Acceleration)
Let: Initial velocity = u, Final velocity = v, Acceleration = a, Time = t, Displacement = s.
v = u + at
\(\displaystyle s = ut + \frac{1}{2}at^2\)
\(\displaystyle v^2 = u^2 + 2as\)
\(\displaystyle s = \frac{(u + v)}{2}t\)
- Distance in nth second:
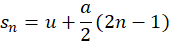
- Using calculus:
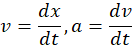
Integrating,
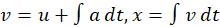
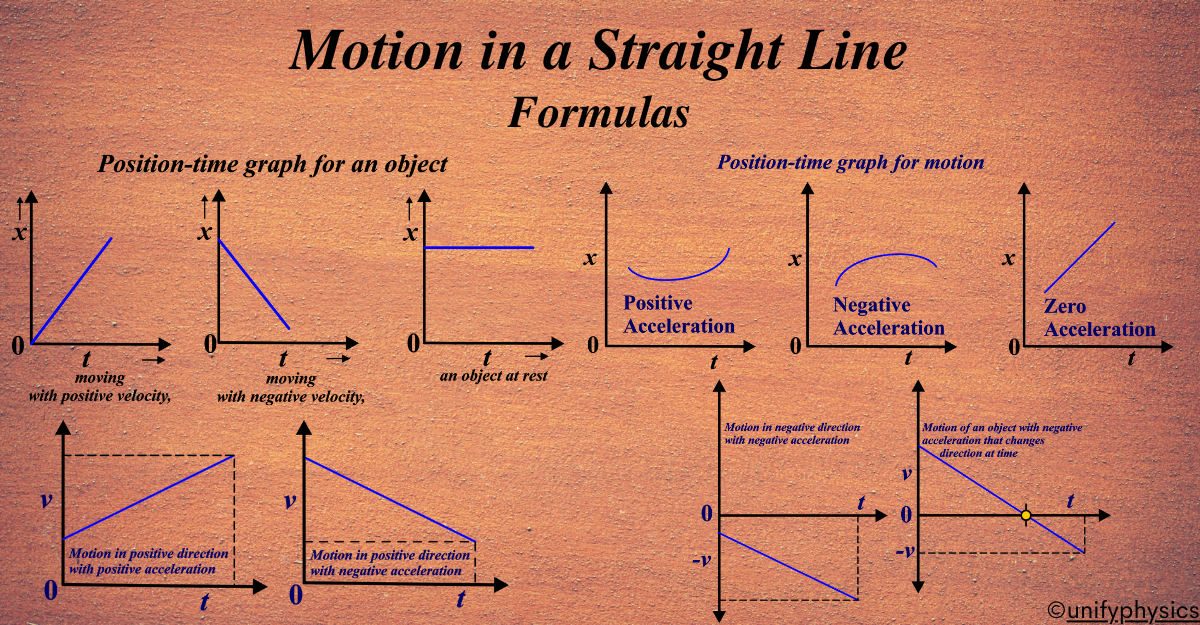
Graphical Interpretation
Position–Time (x–t) Graph
- Slope = velocity
- Straight line → uniform motion
- Curved → accelerated motion
Velocity–Time (v–t) Graph
- Slope = acceleration
- Area under v–t curve = displacement
Acceleration–Time (a–t) Graph
- Area under a–t curve = change in velocity
Motion Under Gravity (Vertical Motion)
Let upward direction be positive and acceleration = g (9.8 m/s² downward).
- For freely falling body:
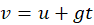
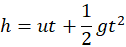
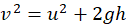
- For body thrown upward:
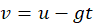
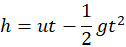
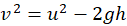
- At maximum height:
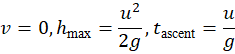
- Total time of flight:
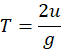
Relative Velocity
- For two objects A and B moving along the same line:
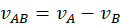
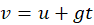
- If moving in same direction:
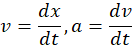
- If moving in opposite direction:
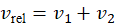
- General vector form:
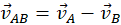
If velocities are inclined at an angle θ:
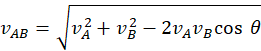
and
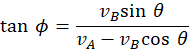
Important Special Results
- Displacement in nth second:
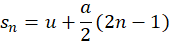
- Stopping Distance:
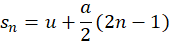
(a = retardation)
- Galileo’s Law of Odd Numbers:
In free fall from rest,
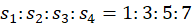
- Reaction Time Experiment:
Ruler drop distance,
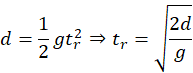
- Distance from v–t graph:

- Acceleration from v–t graph:
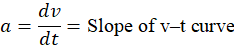
- Average velocity for constant acceleration:
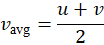
Key Concepts & Short Points
- Displacement can be zero even if motion occurs (e.g., back to start).
- Slope of x–t graph gives velocity.
- Slope of v–t graph gives acceleration.
- Area under v–t graph gives displacement.
- Area under a–t graph gives change in velocity.
- Sign convention is critical: Choose +ve direction and stick to it.
- Instantaneous speed = |Instantaneous velocity|.
- Kinematic equations are valid only for constant acceleration.
- The origin and direction of co-ordinate axes are arbitrary but fixed for the problem.
Dimensional Formulas
| Quantity | Symbol | Dimensions |
| Displacement | x | [L] |
| Velocity | v | [L T⁻¹] |
| Acceleration | a | [L T⁻²] |
| Time | t | [T] |
Graph Shapes Summary
- Uniform motion: x–t → straight line
- Uniform acceleration: x–t → parabola
- Uniform retardation: x–t → inverted parabola
- Uniform velocity: v–t → horizontal line
- Uniform acceleration: v–t → straight sloping line