The story of Ampere’s Law begins with a remarkable discovery in the early 19th century. In 1820, Danish physicist Hans Christian Ørsted found that an electric current creates a magnetic field around it. This was observed when a compass needle placed near a wire carrying an electric current turned to align perpendicularly to the wire. Ørsted’s experiment showed that electricity and magnetism were related, which was a groundbreaking revelation at the time.
Inspired by Ørsted’s discovery, French physicist André-Marie Ampère began experimenting with the magnetic force between two current-carrying wires. He found that the force was directly related to the amount of current and the length of the wires. This led to the formulation of Ampère’s force law, which describes the interaction between two parallel current-carrying conductors.
Ampère’s work laid the foundation for what would become Ampère’s Law. His experiments and mathematical descriptions were pivotal in establishing the relationship between electric currents and the magnetic fields they produce.
In the 1850s, Scottish physicist James Clerk Maxwell expanded on Ampère’s findings. Maxwell was able to generalize these results into a single mathematical framework. He introduced the concept of the displacement current, which allowed Ampère’s Law to account for changing electric fields, not just steady currents. This modification was crucial for the development of Maxwell’s equations, which are the basis of classical electromagnetism.
Maxwell’s contributions transformed Ampère’s Law into a more comprehensive and versatile tool. The modern form of Ampère’s Law, sometimes called the Ampère-Maxwell Law, is one of the four Maxwell equations that define the entire field of electromagnetism.
What Is Ampere’s Law?
Ampere’s Law relates the integrated magnetic field around a closed loop to the electric current passing through the loop. It essentially tells us that the magnetic field can be determined by the amount of electric current flowing.
Imagine you have a garden hose with water flowing through it. The amount of water coming out of the hose depends on how much water is flowing inside it, right? Similarly, Ampere’s Law tells us about the ‘flow’ of a magnetic field around a wire due to the electric current flowing through it.
In more technical terms, Ampere’s Law states that for any closed loop or path, the sum of the length elements times the magnetic field in the direction of the length element is proportional to the electric current enclosed in the loop. This might sound complex, but it’s like saying the strength of the magnetic field created by a current is related to how much current there is.
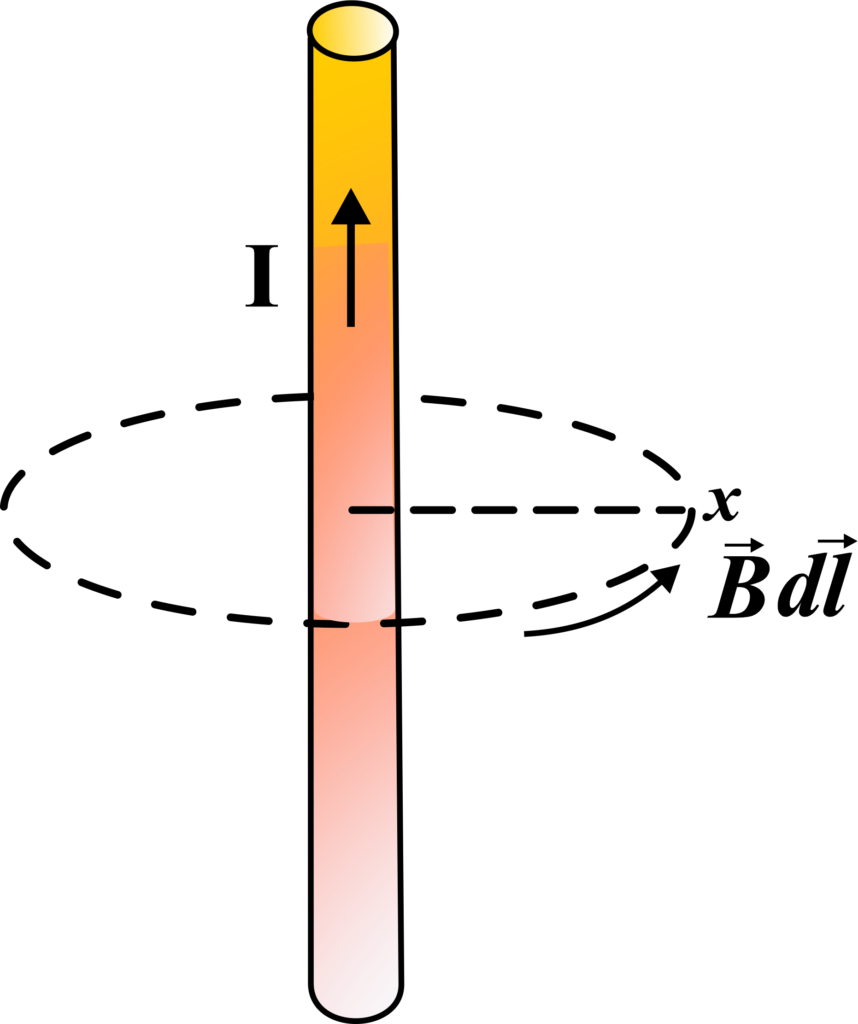
Let’s take a simple example. If you have a straight wire carrying an electric current, it creates a magnetic field around it. This magnetic field forms circular loops around the wire. Now, if you were to take an imaginary loop around this wire and measure the magnetic field along this loop, Ampere’s Law helps you relate this magnetic field to the current flowing through the wire.
The formula for Ampere’s Law looks like this:
\(\displaystyle \oint \vec{B} \cdot d\vec{l} = \mu_0 I_{enc} \)
If you wrap a loop around a wire, the total ‘push’ you feel from the magnetic field as you go around the loop is equal to a constant times the electric current that’s inside the loop. It’s like saying the total ‘squeeze’ you feel from the water pressure as you go around the hose is related to how much water is flowing through it.
Determining Magnetic Field by Ampere’s Law
We’ll start with a straight, long, current-carrying conductor and use Ampere’s Law to find the magnetic field at a point a distance (r) away from the wire. The law is given by the equation:
$$ \oint \vec{B} \cdot d\vec{l} = \mu_0 I_{enc} $$
This means we sum up the magnetic field (\(\displaystyle \vec{B} \)) along a closed loop multiplied by the differential length element (\(\displaystyle d\vec{l}\) ). It equals the permeability of free space (µ0) times the enclosed current (Ienc).
For a long straight wire, we choose a circular path (Amperian loop) centered on the wire because the magnetic field is symmetrical around the wire. This symmetry means the magnetic field (B) is constant at every point on the Amperian loop.
Since (B) is constant along the loop and the direction of (B) is always tangent to the loop, we can pull (B) out of the integral:
\(\displaystyle B \oint dl = \mu_0 I_{enc} \)
The integral (\(\displaystyle\oint dl \)) is just the circumference of the circle, which is (\(\displaystyle 2\pi r \)).
Plugging in the circumference, we get:
\(\displaystyle B(2\pi r) = \mu_0 I_{enc} \)
Solving for (B), we find:
\(\displaystyle B = \frac{\mu_0 I_{enc}}{2\pi r} \)
This result tells us that the magnetic field (B) at a distance (r) from a long straight wire carrying a current (Ienc) decreases as we move away from the wire. It also tells us that (B) is directly proportional to the current (Ienc).
To help students visualize this, you can think of the magnetic field lines as ripples in a pond. If you throw a stone (the electric current) into the water, ripples (magnetic field lines) form in circles around the stone. The further away you are from where the stone hit the water, the weaker the ripples become. This is similar to how the magnetic field decreases with distance from the wire.
Maxwell’s Modifications of Ampere’s Law
To understand Maxwell’s modifications, we first need to remember what Ampere’s Law says. Ampere’s Law tells us that the magnetic field in space can be determined by the electric current flowing through a wire. But there was a problem with this law that James Clerk Maxwell noticed.
The Problem with Ampere’s Law: Ampere’s Law worked well for steady currents, but it didn’t account for situations where the electric field was changing, such as in a charging or discharging capacitor. Maxwell realized that even when there’s no current flowing through a space, a changing electric field in that space could still produce a magnetic field.
Maxwell’s Insight: Maxwell proposed that a changing electric field should be treated similarly to a direct electric current in Ampere’s Law. This was based on the symmetry between electricity and magnetism, where a changing magnetic field can induce an electric field (Faraday’s Law). So, Maxwell suggested that a changing electric field should also be able to induce a magnetic field.
James Clerk Maxwell added a term to account for the changing electric field, leading to the displacement current concept, which completes Ampere’s Law for cases where the electric field changes over time.
Maxwell added a term to Ampere’s Law to include the effects of a changing electric field. The modified equation looks like this:
\(\displaystyle \oint \vec{B} \cdot d\vec{l} = \mu_0 I_{enc} + \mu_0 \epsilon_0 \frac{d\Phi_E}{dt} \)
Here, (\(\displaystyle\frac{d\Phi_E}{dt} \)) represents the rate of change of electric flux, which is akin to a flow of electric field lines through a surface. The term (\(\displaystyle\mu_0 \epsilon_0 \frac{d\Phi_E}{dt} \)) is known as the displacement current, which acts like an additional source of magnetic field³.
Maxwell’s modification is crucial because it completes Ampere’s Law, making it applicable to all scenarios, including those with changing electric fields. This led to the prediction of electromagnetic waves—ripples of electric and magnetic fields that travel through space, which include visible light, radio waves, and X-rays.
Think of it like this: if you have a pond (space) and you throw a stone (electric current), it creates ripples (magnetic field). Now, imagine instead of throwing a stone, you just move your hand back and forth in the water (changing the electric field), it still creates ripples. Maxwell’s modification says that both the stone and the moving hand can create ripples in the pond of space.
Maxwell’s modifications have profound implications. They are the reason we can have wireless communications today. Without this understanding, we wouldn’t have radio, TV, or Wi-Fi! So, Maxwell’s contribution was like adding a missing piece to a puzzle, which not only completed the picture but also showed us a whole new image we didn’t know was part of the scene.
What Is Ampere’s Circuital Law?
Ampere’s Circuital Law is like a special rule that helps us figure out the magnetic field created by electric currents. It’s a bit like a detective’s tool for finding clues about the invisible magnetic fields around wires and coils.
Ampere’s Circuital Law is another form of Ampere’s Law, which is used to calculate the magnetic field in a loop-shaped path, especially when dealing with symmetrical situations like coils and solenoids.
The law says that if you take an imaginary loop around a current-carrying wire and add up the magnetic field along this loop, it will tell you something about the current that’s flowing through the wire. It’s like following a trail that leads you back to the source—the electric current.
Mathematically, Ampere’s Circuital Law is written as:
\(\displaystyle \oint \vec{B} \cdot d\vec{l} = \mu_0 I_{enc} \)
- (\(\displaystyle \oint \vec{B} \cdot d\vec{l}\) ) is the sum of the magnetic field (\(\displaystyle\vec{B}\)) times little bits of the loop (( d\vec{l} )) all the way around.
- (µ0) is just a constant that tells us how strong the magnetic field is in space.
- (Ienc) is the total electric current that’s inside the loop.
If you imagine walking around a path that encloses a wire, the total ‘magnetic push’ you calculate on this walk is directly related to the amount of current flowing through the wire. It’s like saying the total number of footprints you count on a path tells you how many people walked by.
This law is super handy because it works best in symmetrical situations, like a straight wire or a coil, where the magnetic field is nice and even. It makes calculating the magnetic field much easier than having to measure it at every single point.
Proof of Ampere’s Circuital Law
The proof involves integrating the magnetic field along a path enclosing the current. For:
Ampere’s Circuital Law for a Regular Coil
Consider a regular coil, like a spring or a spiral notebook wire, carrying some electric current (I). We want to use Ampere’s Circuital Law to prove that the magnetic field around this coil is related to the current it carries.
The law states that the line integral of the magnetic field (\(\displaystyle\vec{B}\)) around a closed path is equal to the permeability of free space (µ0) times the current passing through the loop:
\(\displaystyle \oint \vec{B} \cdot d\vec{l} = \mu_0 I \)
Take a tiny piece of the loop, (dl), and look at the magnetic field (\(\displaystyle\vec{B} \)) at this point. Because we’re dealing with a regular coil, the magnetic field will be the same all around the conductor.
Let’s say there’s a small angle (θ) between (dl) and (\(\displaystyle\vec{B}\)). But since we’re considering a regular coil, we can assume (θ= 0∘), meaning (\(\displaystyle\vec{B}\)) and (dl) are parallel.
From previous knowledge, we know that the magnetic field (B) at a point (P) at a perpendicular distance (r) from a long straight conductor carrying current (I) is given by:
\(\displaystyle B = \frac{\mu_0 I}{2\pi r} \)
Because the coil is regular, the magnetic field doesn’t vary at a distance (r). So, the integral of an element will form the whole circle of the circumference (\(\displaystyle2\pi r\)):
\(\displaystyle \oint dl = 2\pi r \)
Put the value of (B) and (\(\displaystyle\oint dl\)) in the equation, we get:
\(\displaystyle B \oint dl = \frac{\mu_0 I}{2\pi r} \times 2\pi r = \mu_0 I \)
Therefore, we have shown that:
\(\displaystyle \oint \vec{B} \cdot d\vec{l} = \mu_0 I \)
This confirms Ampere’s Circuital Law for a regular coil. Think of the coil as a hose with water flowing through it. The magnetic field is like the pressure of the water coming out of the hose. Just as the water pressure is consistent all around the hose, the magnetic field is consistent all around the coil. By following the steps of the proof, we’ve shown that the ‘pressure’ (magnetic field) is directly related to how much ‘water’ (current) is flowing through our ‘hose’ (coil).
Ampere’s Circuital Law for an Irregular Coil
An irregular coil does not have a constant radius or shape, like a squiggly line or a loop with varying sizes. Proving Ampere’s Law for such a coil involves a bit more complexity than a regular coil.
We begin with the same principle:
\(\displaystyle \oint \vec{B} \cdot d\vec{l} = \mu_0 I_{enc} \)
For an irregular coil, we select an Amperian loop that best fits the symmetry of the situation. The loop might not be a perfect circle due to the irregularity of the coil.
We perform the integral along the loop, taking into account the varying radius (r) and the angle (θ) between (\(\displaystyle\vec{B}\)) and (\(\displaystyle d\vec{l}\)). The integral becomes:
\(\displaystyle \oint \vec{B} \cdot d\vec{l} = \oint \frac{\mu_0 I}{2\pi r} \cdot dl \)
Here, (dl) represents a small segment of the loop, and (r) is the distance from the current element to the point on the loop.
Since the radius (r) is not constant, we cannot simply multiply by (\(\displaystyle 2\pi r \)) as we did for the regular coil. Instead, we use calculus to integrate along the path, considering the changing radius and the angle (θ).
After performing the integration, we find that the integral still equals (\(\displaystyle \mu_0 I \)), confirming Ampere’s Circuital Law even for an irregular coil.
Imagine walking along a winding mountain path (the irregular coil) with a compass (to measure the magnetic field). As you walk, the direction and steepness of the path change, just like the radius and angle in our integral. By adding up all the little changes in direction and steepness (the integral), you can still figure out how much you’ve ascended or descended in total (the enclosed current). The proof for an irregular coil shows that Ampere’s Circuital Law is robust and applies to all kinds of shapes and paths, not just simple ones.
Ampere’s Circuital Law with Varying Current Density
When dealing with a coil that has varying current densities, the proof of Ampere’s Circuital Law becomes more complex.
The law still begins with the same principle:
\(\displaystyle \oint \vec{B} \cdot d\vec{l} = \mu_0 I_{enc} \)
However, (Ienc) now represents the total current passing through the loop, which varies due to the changing current density.
Current density (\(\displaystyle\vec{J}\)) is the amount of current per unit area, and it can vary across different parts of the coil. It’s given by:
\(\displaystyle \vec{J} = \frac{dI}{dA} \)
where (dI) is the differential current through a differential area (dA). To find the total current enclosed (Ienc), we integrate the current density over the cross-sectional area (A) that the Amperian loop encloses:
\(\displaystyle I_{enc} = \int_A \vec{J} \cdot d\vec{A} \)
Now, we use the integrated current density in Ampere’s Law:
\(\displaystyle \oint \vec{B} \cdot d\vec{l} = \mu_0 \int_A \vec{J} \cdot d\vec{A} \)
The magnetic field (\(\displaystyle\vec{B}\)) still needs to be integrated around the Amperian loop. However, due to the varying current density, the magnetic field may not be uniform and could vary along the path.
The integration becomes more complex as both (\(\displaystyle\vec{B}\)) and (\(\displaystyle\vec{J}\)) can vary along the path and across the area. After performing the integration, if done correctly, the equation will still hold, confirming Ampere’s Circuital Law even with varying current densities.
To simplify this for students, imagine a river with varying flow speeds—some parts are fast, and others are slow. The total amount of water (current) that passes through a section of the riverbank (Amperian loop) depends on these varying speeds (current density). Just as you would measure the flow at different points to find the total water passing through, we integrate the varying current density to find the total current enclosed by the loop.
Applications Of Ampere’s Circuital Law
Magnetic Induction by a Long Wire
One of the key applications of Ampere’s Circuital Law is to calculate the magnetic field, or magnetic induction, created by a long current-carrying wire. Imagine a long straight wire with electric current flowing through it. This current generates a magnetic field around the wire. The field forms circular loops around the wire, and its strength can be calculated at any distance (r) from the wire using Ampere’s Circuital Law.
Ampere’s Circuital Law provides a straightforward method to determine the magnetic field (B) at a distance (r) from the wire. The law states:
\(\displaystyle \oint \vec{B} \cdot d\vec{l} = \mu_0 I_{enc} \)
where (\(\displaystyle\oint \vec{B} \cdot d\vec{l}\)) is the line integral of the magnetic field around a closed loop, (µ0) is the permeability of free space, and (Ienc) is the current enclosed by the loop.
We select an imaginary circular path around the wire at the distance (r) where we want to calculate the magnetic field. Since the magnetic field is symmetrical and constant at a given distance from the wire, the law simplifies to:
\(\displaystyle B \cdot 2\pi r = \mu_0 I \)
Rearrange the equation to find the magnetic field (B):
\(\displaystyle B = \frac{\mu_0 I}{2\pi r} \)
This equation tells us that the magnetic field decreases as the distance (r) increases. It also shows that the field is directly proportional to the current (I).
To visualize this, think of the wire as a garden hose. The water coming out represents the magnetic field. The further you move from the hose, the less water you feel. Similarly, the further you are from the wire, the weaker the magnetic field.
Magnetic Field Inside and Outside a Conducting Cylinder
Consider a long cylinder, like a pipe, and it’s made of a conducting material. When an electric current flows through this cylinder, it creates a magnetic field around it. A cylinder is made of a material that allows electric current to flow through it. The flow of electric charge through the cylinder. The invisible force field forms around the cylinder due to the current.
If the cylinder is solid and the current is evenly distributed, the magnetic field inside the cylinder increases linearly from the center to the surface. Beyond the surface, the magnetic field behaves like that of a long straight wire, decreasing with distance from the surface. Imagine a long, straight, cylindrical wire carrying a steady current (I). We want to find the magnetic field both inside and outside this wire.
Inside the Cylinder: For the inside of the cylinder, we’ll assume the current is uniformly distributed. The current density (J) (current per unit area) is given by:
\(\displaystyle J = \frac{I}{\pi R^2} \)
where (R) is the radius of the cylinder. Using Ampere’s Circuital Law, we take an imaginary circular path (Amperian loop) of radius (r) (where (r < R)) inside the cylinder. The law states:
\(\displaystyle \oint \vec{B} \cdot d\vec{l} = \mu_0 I_{enc} \)
The enclosed current (Ienc) is the current density times the area of the circle of radius (r):
\(\displaystyle I_{enc} = J \pi r^2 = \frac{I}{\pi R^2} \pi r^2 = I \left(\frac{r^2}{R^2}\right) \)
Since the magnetic field (B) is the same all around the path and points tangentially, we can pull it out of the integral:
\(\displaystyle B \oint dl = B(2\pi r) = \mu_0 I_{enc} \)
Solving for (B), we get:
\(\displaystyle B = \frac{\mu_0 I}{2\pi r} \left(\frac{r^2}{R^2}\right) \)
\(\displaystyle B = \frac{\mu_0 I r}{2\pi R^2} \)
Outside the Cylinder: For points outside the cylinder (where ( r \geq R )), the entire current ( I ) is enclosed by the Amperian loop. The magnetic field ( B ) at distance ( r ) from the center of the wire is given by:
\(\displaystyle B = \frac{\mu_0 I}{2\pi r} \)
The magnetic field inside a long current-carrying cylinder increases linearly with distance from the center, while outside, it decreases with distance. This derivation shows how Ampere’s Circuital Law can be applied to different scenarios to predict the behavior of magnetic fields around conductors.
Magnetic Field of a Hollow Conducting Cylinder
Imagine a hollow cylinder, like a pipe, with current flowing along its surface. We want to find the magnetic field this current generates at different points. A cylinder with no current flowing inside, only on its surface. The flow of electric charge along the surface of the cylinder. The invisible force field we’re trying to find.
Ampere’s Circuital Law is our tool to calculate the magnetic field. It states:
\(\displaystyle \oint \vec{B} \cdot d\vec{l} = \mu_0 I_{enc} \)
Inside the Cylinder: For points inside the hollow cylinder, no current is enclosed by the Amperian loop. Therefore, (Ienc = 0 ), and the magnetic field (B) is:
B = 0
This means there is no magnetic field inside the hollow cylinder.
On the Surface of the Cylinder: On the surface, the current is still not enclosed by the loop, so (B) remains:
B = 0
Outside the Cylinder: For points outside the cylinder, the entire current (I) is enclosed by the Amperian loop. The magnetic field (B) at distance (r) from the center of the cylinder is given by:
\(\displaystyle B = \frac{\mu_0 I}{2\pi r} \)
This is the same as the field around a long straight wire because the current is effectively concentrated in a wire at the surface of the cylinder.
To visualize this, think of the hollow cylinder as a tube wrapped with a thin layer of flowing water (the current). Inside the tube, there’s no water flow, so no pressure (magnetic field). Outside the tube, the water flow creates pressure (magnetic field) that decreases as you move away from the tube. The magnetic field due to a conducting current-carrying hollow cylinder is zero inside and behaves like the field of a straight wire outside.
Also Read: Solenoid
Applications of Ampere’s Law
Ampere’s Law is like a Swiss Army knife for physicists and engineers—it has a variety of uses, especially when it comes to understanding and designing systems involving magnetic fields and electric currents. Here are some of the key applications:
Determining Magnetic Fields: Ampere’s Law helps us calculate the magnetic field created by different configurations of current-carrying wires. For example, it can tell us the magnetic field around a long straight wire or inside a coil of wire (solenoid).
Designing Electrical Devices: Knowing the magnetic field is crucial for designing electrical devices like transformers, inductors, and motors. These devices are everywhere—from the power supply on your computer to the engine in an electric car.
Understanding Magnetic Materials: Ampere’s Law is used to study the behavior of magnetic materials and how they interact with electric currents. This is important for creating and improving magnetic storage devices, like hard drives.
Medical Technology: In medicine, Ampere’s Law is part of the principle behind MRI machines, which use strong magnetic fields to create images of the inside of the body.
Telecommunications: The law also plays a role in telecommunications, where understanding magnetic fields helps in designing antennas and other communication components.
Physics Research: In research, Ampere’s Law is used to understand fundamental physical phenomena, such as the behavior of plasmas, which are important in fields like astrophysics and fusion energy research.
To make these applications more relatable, think of Ampere’s Law as a recipe that tells us how to mix electric currents and magnetic fields to ‘bake’ all sorts of technological ‘treats’. Just like a chef needs to know how different ingredients interact to create a dish, scientists and engineers use Ampere’s Law to understand and create systems that shape our modern world.
Limitations of Ampere’s Law
Ampere’s Law is incredibly useful, but it has its boundaries.
Steady Currents Only: Ampere’s Law works perfectly when dealing with steady currents—currents that don’t change over time. It’s like having a steady stream of water in a pipe; the flow doesn’t speed up or slow down.
No Time-Varying Fields: The law doesn’t hold up when you have to change electric fields, like when you’re charging or discharging a capacitor. That’s because Ampere’s Law doesn’t consider the effects of a changing electric field on the magnetic field.
Symmetrical Situations: Ampere’s Law is most effective in symmetrical situations, like a long straight wire or a tightly wound coil (solenoid). When things get asymmetrical, the law becomes much harder to apply, and the calculations can get very complicated.
Displacement Current: This is where Maxwell’s modification comes in. Maxwell added a term called the “displacement current” to account for changing electric fields. This term fixes the problem with Ampere’s Law and makes it complete, allowing it to work even when electric fields are changing.
Think of Ampere’s Law as a recipe that works well for a specific dish. If you stick to the recipe, you’ll get a great result every time. But if you start changing the ingredients—like using a different kind of current or a changing electric field—the recipe doesn’t work anymore. That’s when you need to tweak the recipe, which is what Maxwell did with his modification.
Solved Examples
Problem 1: A long straight wire carries a current of (I = 20 A). Calculate the magnetic field at a distance (r = 0.5 m) from the wire using Ampere’s Circuital Law.
Solution: Ampere’s Circuital Law states:
\(\displaystyle \oint \mathbf{B} \cdot d\mathbf{l} = \mu_0 I_{\text{enc}} \)
For a long straight wire, the magnetic field (B) at a distance (r) from the wire is:
\(\displaystyle B = \frac{\mu_0 I}{2\pi r} \)
Given: (I = 20 A), (r = 0.5 m), (\(\displaystyle\mu_0 = 4\pi \times 10^{-7} \, \text{T} \cdot \text{m/A}\))
\(\displaystyle B = \frac{4\pi \times 10^{-7} \times 20}{2\pi \times 0.5} \)
\(\displaystyle B = \frac{8\pi \times 10^{-7} \times 20}{2\pi \times 0.5} \)
\(\displaystyle B = \frac{8 \times 10^{-7} \times 20}{0.5} \)
\(\displaystyle B = \frac{16 \times 10^{-6}}{0.5} \)
\(\displaystyle B = 32 \times 10^{-6} \, \text{T} \)
\(\displaystyle B = 3.2 \times 10^{-5} \, \text{T} \)
The magnetic field at a distance (0.5 m) from the wire is (\(\displaystyle 3.2 \times 10^{-5} \, \text{T} \)).
Problem 2: A toroid has 1000 turns of wire and carries a current of (2 A). The mean radius of the toroid is (10 cm). Calculate the magnetic field inside the toroid.
Solution: The magnetic field (B) inside a toroid is given by:
\(\displaystyle B = \frac{\mu_0 N I}{2 \pi r} \)
\(\displaystyle B = \frac{4\pi \times 10^{-7} \times 1000 \times 2}{2 \pi \times 0.1} \)
\(\displaystyle B = \frac{4\pi \times 10^{-4}}{0.1} \)
\(\displaystyle B = \frac{4\pi \times 10^{-4}}{0.1} \)
\(\displaystyle B = 4 \times 10^{-3} \, \text{T} \)
\(\displaystyle B \approx 4 \times 10^{-3} \, \text{T} \)
The magnetic field inside the toroid is (\(\displaystyle 4 \times 10^{-3} \, \text{T} \)).
Problem 3: A cylindrical wire of radius (R = 5 mm) carries a current (I = 10 A) with a current density (J) varying as (\(\displaystyle J = J_0 \frac{r}{R} \)). Find the magnetic field at a distance (r = 3 mm) from the axis.
Solution: The current density (J) is given by:
\(\displaystyle J = J_0 \frac{r}{R} \)
The total current (I) is given by:
\(\displaystyle I = \int_0^R J \cdot 2\pi r \, dr = \int_0^R J_0 \frac{r}{R} \cdot 2\pi r \, dr \)
\(\displaystyle I = \frac{2\pi J_0}{R} \int_0^R r^2 \, dr = \frac{2\pi J_0}{R} \cdot \frac{R^3}{3} = \frac{2\pi J_0 R^2}{3} \)
\(\displaystyle J_0 = \frac{3I}{2\pi R^2} \)
So,\(\displaystyle J = \frac{3I}{2\pi R^3} r \)
Using Ampere’s Circuital Law for (r < R),
\(\displaystyle B \cdot 2\pi r = \mu_0 \int_0^r J \cdot 2\pi r’ \, dr’ \)
\(\displaystyle B \cdot 2\pi r = \mu_0 \cdot \frac{3I}{2\pi R^3} \cdot 2\pi \int_0^r r’^2 \, dr’ \)
\(\displaystyle B \cdot 2\pi r = \mu_0 \cdot \frac{3I}{R^3} \cdot \frac{r^3}{3} \)
\(\displaystyle B \cdot 2\pi r = \mu_0 \cdot \frac{I r^3}{R^3} \)
\(\displaystyle B = \frac{\mu_0 I r^2}{2\pi R^3} \)
Given: (I = 10 A), (R = 0.005 m), (r = 0.003 m), (\(\displaystyle\mu_0 = 4\pi \times 10^{-7} \, \text{T} \cdot \text{m/A} \))
\(\displaystyle B = \frac{4\pi \times 10^{-7} \times 10 \times (0.003)^2}{2\pi \times (0.005)^3} \)
\(\displaystyle B = \frac{4 \times 10^{-6} \times 9 \times 10^{-6}}{2 \times 125 \times 10^{-9}} \)
\(\displaystyle B = \frac{36 \times 10^{-12}}{250 \times 10^{-9}} \)
\(\displaystyle B = \frac{36 \times 10^{-12}}{250 \times 10^{-9}} \)
\(\displaystyle B = 1.44 \times 10^{-4} \, \text{T} \)
The magnetic field at a distance (3 mm) from the axis is (\(\displaystyle 1.44 \times 10^{-4} \, \text{T} \)).
Problem 4: A circular coil of radius (r = 0.1m) and 50 turns carries a current of (3 A). Calculate the magnetic field at the center of the coil.
Solution: The magnetic field (B) at the center of a circular coil is given by:
\(\displaystyle B = \frac{\mu_0 N I}{2r} \)
Given: ( N = 50 ), (I = 3 A), (r = 0.1 m), (\(\displaystyle\mu_0 = 4\pi \times 10^{-7} \, \text{T} \cdot \text{m/A}\) )
\(\displaystyle B = \frac{4\pi \times 10^{-7} \times 50 \times 3}{2 \times 0.1} \)
\(\displaystyle B = \frac{4\pi \times 10^{-7} \times 150}{0.2} \)
\(\displaystyle B = \frac{600\pi \times 10^{-7}}{0.2}\)
\(\displaystyle B = 3000\pi \times 10^{-7} \)
\(\displaystyle B = 3 \pi \times 10^{-4} \, \text{T} \)
\(\displaystyle B \approx 9.42 \times 10^{-4} \, \text{T} \)
The magnetic field at the center of the coil is (\(\displaystyle 9.42 \times 10^{-4} \, \text{T} \)).
Problem 5: An irregular coil with varying radius and 100 turns carries a current of (1 A). The radius varies such that the average radius is (0.05 m). Calculate the approximate magnetic field at the center of the coil.
Solution: For an irregular coil, we can approximate the magnetic field using the average radius:
\(\displaystyle B = \frac{\mu_0 N I}{2r_{\text{avg}}} \)
Given: (N = 100), (I = 1 A), (ravg = 0.05 m), (\(\displaystyle\mu_0 = 4\pi \times 10^{-7} \, \text{T} \cdot \text{m/A}\) )
\(\displaystyle B = \frac{4\pi \times 10^{-7} \times 100 \times 1}{2 \times 0.05} \)
\(\displaystyle B = \frac{4\pi \times 10^{-7} \times 100}{0.1} \)
\(\displaystyle B = \frac{400\pi \times 10^{-7}}{0.1} \)
\(\displaystyle B = 4000\pi \times 10^{-7} \)
\(\displaystyle B = 4 \pi \times 10^{-3} \, \text{T} \)
\(\displaystyle B \approx 12.57 \times 10^{-3} \, \text{T} \)
The approximate magnetic field at the center of the irregular coil is (\(\displaystyle 12.57 \times 10^{-3} \, \text{T}\) ).
FAQs
What is Ampere’s Law and what does it describe?
Ampere’s Law describes the relationship between an electric current and the magnetic field it generates. Specifically, it states that the integral of the magnetic field around a closed loop is proportional to the total current passing through the loop. This law helps in understanding how currents produce magnetic fields in different geometrical configurations.
How is Ampere’s Circuital Law useful in calculating magnetic fields?
Ampere’s Circuital Law is particularly useful for calculating magnetic fields in systems with high symmetry, such as long straight wires, solenoids, and toroids. By applying this law to these symmetrical situations, one can easily derive expressions for the magnetic field without complex integration, simplifying the analysis of magnetic fields in practical applications.
What are the key differences between Ampere’s Law and Biot-Savart Law?
The key difference is that Ampere’s Law is typically used in situations with high symmetry, where it simplifies the calculation of the magnetic field, while the Biot-Savart Law can be applied to any shape of a current-carrying conductor but often requires more complex integration. Ampere’s Law focuses on the total current passing through a loop, whereas the Biot-Savart Law calculates the contribution to the magnetic field from each small segment of the current.
What are the limitations of Ampere’s Law in practical applications?
The primary limitation of Ampere’s Law is that it is most effective in situations with symmetrical current distributions. In cases where the geometry of the current path is complex or lacks symmetry, applying Ampere’s Law directly can be difficult, and other methods like the Biot-Savart Law might be more appropriate.
How did Maxwell modify Ampere’s Law and why was this modification necessary?
Maxwell modified Ampere’s Law by adding a term that accounts for the changing electric field, known as the displacement current. This modification was necessary to address the inconsistency in Ampere’s Law when applied to situations where the electric field is changing over time, such as in capacitors during charging and discharging. Maxwell’s addition ensures the continuity of the magnetic field even in the absence of a physical current.
What is the significance of Maxwell’s modification of Ampere’s Law in electromagnetism?
Maxwell’s modification of Ampere’s Law is significant because it completes the set of equations known as Maxwell’s equations, which form the foundation of classical electromagnetism. This modification unified the description of electric and magnetic fields, leading to the prediction of electromagnetic waves and the understanding that light itself is an electromagnetic wave.
Can Ampere’s Circuital Law be applied to non-steady currents? Explain.
In its original form, Ampere’s Circuital Law applies to steady (constant) currents. However, with Maxwell’s modification, which includes the displacement current, the law can be applied to non-steady (time-varying) currents. This extended form of the law accounts for both the conduction current and the displacement current, making it applicable to a wider range of electromagnetic phenomena, including alternating current (AC) circuits and electromagnetic waves.
