The story of the toroid begins with the foundational work of Michael Faraday, a pioneering scientist in the field of electromagnetism. In 1830, Faraday made a groundbreaking discovery that would lead to the invention of the toroid.
Faraday observed that when a magnetic field changes over time, it induces an electric voltage in a nearby wire. This phenomenon, known as electromagnetic induction, is a fundamental principle of electromagnetism and is the operating principle behind many electrical devices and systems.
Building on this principle, Faraday invented the first toroid. He took a wire and wound it around a ring-shaped core to create a closed-loop coil. This design was significant because it allowed the magnetic field generated by the current in the wire to remain confined within the core of the toroid, creating a very efficient magnetic system.
The term “toroid” itself comes from the word “torus,” which is a mathematical term for a doughnut-shaped figure. The earliest known use of the word “toroid” dates back to the 1880s, and it was first recorded in the writings of George Carr.
The toroid’s unique shape and the way it confines the magnetic field have made it an essential component in modern electrical engineering. It’s used in a variety of applications, from transformers to inductors, and continues to be a topic of study and innovation in physics and engineering.
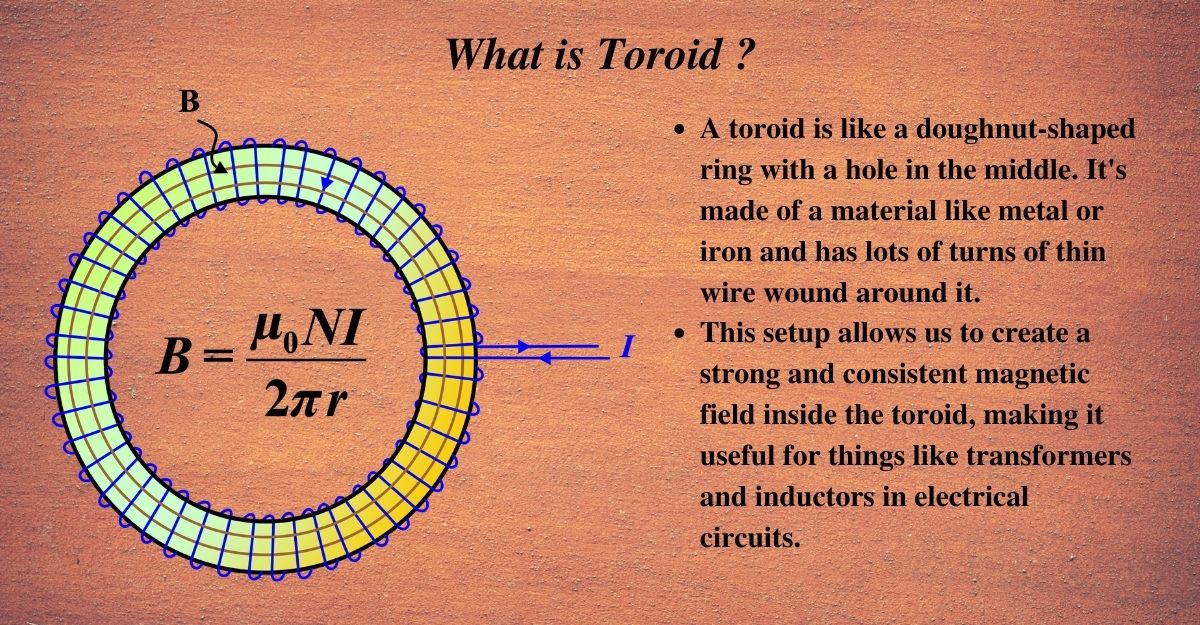
What is a Toroid?
A toroid is a doughnut-shaped object, which in physics, particularly electromagnetism, refers to a coil of wire wound around a circular ring. This shape is crucial because it confines the magnetic field to its core.
Imagine a doughnut or a ring-shaped cushion. A toroid is very much like that in shape. In the world of physics, when we talk about a toroid, we’re referring to a specific type of coil. It’s a coil of wire that’s wrapped around a donut-shaped core. This core can be made of different materials, such as metal or air*.
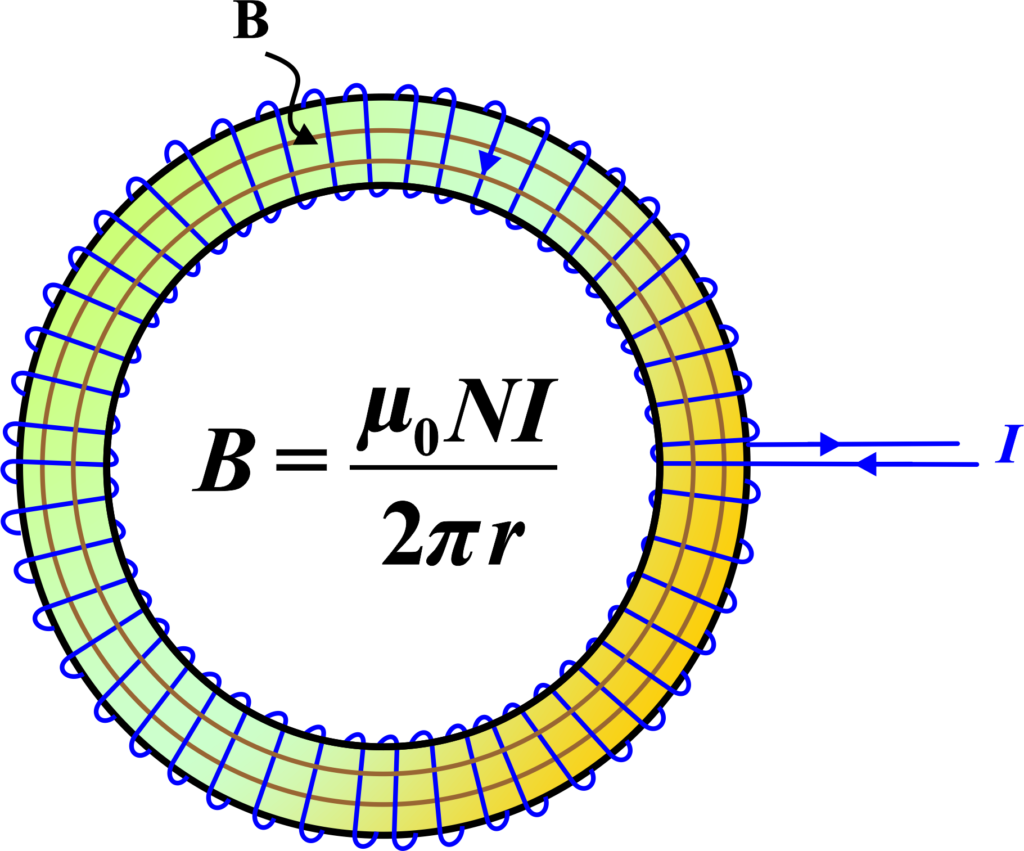
Now, why is this shape interesting or useful? The magic of a toroid lies in its ability to contain a magnetic field within itself. When an electric current flows through the wire, it creates a magnetic field. But unlike other shapes, the toroid keeps this magnetic field wrapped up inside the donut, without letting it spread out too much. This makes the toroid a very tidy and efficient way to manage magnetic fields.
The toroid is a practical shape because it’s compact and doesn’t waste much space. It’s like a neat, self-contained package of magnetic field lines, all swirling around inside the donut, away from other components that might not want to be influenced by the magnetic field.
Note: *An air core toroid is essentially a coil of wire wound in a circular shape without a solid core material. The space within and around the turns of the wire is filled with air (or any non-magnetic material), which acts as the core.
Formula of Toroid
When we talk about the formulas of a toroid, we’re mainly concerned with the magnetic field it creates.
Magnetic Field Inside a Toroid: The primary formula for the magnetic field inside a toroid is derived from Ampere’s Law. It looks like this:
\(\displaystyle B = \frac{\mu_0 N I}{2 \pi r} \)
- (B) is the magnetic field inside the toroid.
- (µ0) is the permeability of free space (a constant value).
- (N) is the total number of turns of the wire.
- (I) is the current flowing through the wire.
- (r) is the radius of the circular path inside the toroid.
Wedge Angle in a Toroid: The wedge angle in a toroid refers to the angle subtended by the center of the toroid for each turn of the wire. It’s a way to describe how the wire is distributed around the toroidal core. The formula for the wedge angle (θ) is given by:
\(\displaystyle \theta = \frac{2 \pi}{n} \text{ radians} \)
- (n) is the number of loops or turns of the wire around the toroid.
This angle helps in understanding the spacing between the turns of the wire. If you have a toroid with a large number of turns, each turn will subtend a smaller angle at the center of the toroid. Conversely, if there are fewer turns, each turn will subtend a larger angle.
Number of Turns in a Toroidal Coil: Sometimes, you might need to calculate the number of turns in a toroidal coil. The relationship between the inner radius of the toroid (A), the radius of the wire (r), and the number of loops (n) is given by the equation:
\(\displaystyle \sin\left(\frac{\pi}{n}\right) = \frac{r}{A – r} \)
This equation helps you understand how tightly the wire can be wound around the toroid’s core¹.
Volume and Surface Area of a Toroid: If you’re dealing with a toroid with a square cross-section, you might use formulas to find its volume (V) and surface area (S):
\(\displaystyle V = 2 \pi R A \)
\(\displaystyle S = 2 \pi R P \)
- (R) is the radius of revolution (from the center of the square to the axis of rotation).
- (A) is the area of the cross-section.
- (P) is the perimeter of the square.
These formulas allow us to calculate how the toroid will interact with electric currents and magnetic fields, which is crucial for their application in devices like transformers and inductors.
Construction of Toroid
Toroids are constructed from a circular ring-shaped magnetic core, typically made from materials like silicon steel, ferrite, or iron powder, and are wound with copper wire.
The Core: A toroid starts with a core that is typically made of a ferromagnetic material like iron, ferrite, or silicon steel. This core is shaped like a doughnut—a circular ring with a hollow center.
The Wire: Around this core, we wind a wire—usually an enameled copper wire. The enamel coating acts as an insulator, preventing the turns of wire from short-circuiting each other.
The Winding Process: The wire is wound tightly around the core, with each turn of the wire lying close to the previous one. This is done to ensure that there is minimal space between the turns, which helps in maintaining the efficiency of the toroid.
Number of Turns: The number of turns of the wire will depend on the intended use of the toroid. More turns will generally increase the inductance of the toroid.
Insulation: Besides the enamel on the wire, additional insulation may be used between layers of wire, especially if the toroid is meant for high-voltage applications.
Securing the Wire: Once the desired number of turns is reached, the wire is secured in place, often with a type of tape or varnish, to prevent it from unwinding or shifting.
Testing: After construction, the toroid is usually tested to ensure that it meets the required specifications, such as inductance, resistance, and strength of the magnetic field.
The construction of a toroid is a careful process that combines materials science with electrical engineering. The goal is to create a component that efficiently channels the magnetic field generated by the current flowing through the wire, with minimal loss or interference.
Working Principle of Toroid
The working principle of a toroid is based on electromagnetism. When an electric current passes through the wire, it generates a magnetic field within the core of the toroid, which is guided along the circular shape. To understand how a toroid works, we need to think about what happens when electricity flows through a wire.
Electromagnetism: The working principle of a toroid is based on the concept of electromagnetism. When an electric current passes through a wire, it creates a magnetic field around the wire. This is the right-hand rule of electromagnetism, where if you point the thumb of your right hand in the direction of the current, your fingers will curl in the direction of the magnetic field.
The Shape of the Toroid: A toroid is essentially a solenoid that’s been bent into a circle. This shape is crucial because it means the magnetic field lines created by the current in the wire are directed along the circular path of the toroid.
Magnetic Field Containment: Because of its unique shape, the magnetic field in a toroid is contained within the core of the toroid. This is different from a straight solenoid, where the magnetic field lines spread out from the ends of the coil.
Ampere’s Law: The strength of the magnetic field inside the toroid can be calculated using Ampere’s Law. This law tells us that the magnetic field along the loop inside the toroid is proportional to the current times and the number of turns of the wire.
Efficiency: The toroid’s design is highly efficient. Since the magnetic field is contained within the donut-shaped core, there is minimal magnetic field leakage, which makes toroids very effective inductors and transformers at low frequencies when large inductances are required.
This principle of electromagnetism and the efficient design of the toroid makes it ideal for use in various electrical devices, such as power supplies and audio equipment, where managing the magnetic field is essential.
Properties of a Toroid
Toroids are known for their high magnetic efficiency and low leakage inductance. They have a uniform magnetic field inside and almost no field outside, making them ideal for minimizing electromagnetic interference. Let’s see a few properties of a toroid in detail,
Shape and Structure: A toroid is essentially a solenoid bent into a circular shape, forming a closed loop. It’s like a doughnut or a ring with a hollow center.
Magnetic Field: One of the key properties of a toroid is that the magnetic field inside it is uniform and circular, following the path of the wire. This field is confined within the core of the toroid, which means outside the toroid, the magnetic field is practically zero.
Winding: The wire used to create a toroid is usually enameled, which means it’s insulated. The turns of the wire are closely wound around the core with very little space between them, making the coil compact and efficient.
Efficiency: Toroids are highly efficient due to their shape, which minimizes the leakage of the magnetic field. This makes them ideal for use in circuits where you want to keep the magnetic field contained, such as in transformers.
Inductance: The inductance of a toroid is generally higher than that of a straight coil (solenoid) of the same length. This is because the closed loop of the toroid helps to concentrate the magnetic field.
Electromagnetic Interference: Due to their design, toroids are excellent at reducing electromagnetic interference (EMI). This is why they’re often used in electronic devices to prevent EMI from affecting other components.
Versatility: Toroids can be made from various materials, including ferrite, iron powder, or silicon steel, depending on the required magnetic properties and the frequency of operation.
Applications: The unique properties of toroids make them suitable for a wide range of applications, from power transformers to inductors in electronic circuits.
Magnetic Field of Toroid
The magnetic field inside a toroid is uniform and tangential to the circular path at any point inside the toroid. It’s calculated using Ampere’s Law and is confined within the core of the toroid.
Imagine you have a doughnut, and you’re able to sprinkle some iron filings all over it. If this doughnut was a toroid with a current running through it, those iron filings would align themselves in a particular pattern. This pattern represents the magnetic field lines.
In a toroid, the magnetic field is quite special because it’s confined within the doughnut’s body. It doesn’t spread out like it would in a straight coil or solenoid. Instead, it forms concentric circles inside the toroid.
When an electric current flows through the wire wrapped around the toroid, it creates a magnetic field. The direction of this magnetic field is tangential to the circular path of the wire. This means if you were a tiny ant walking along the path of the wire, the magnetic field would always be pointing to your left or right, never forward or backward.
To calculate the magnetic field inside the toroid, we’ll use Ampere’s Circuital Law, which relates the magnetic field in a loop to the current passing through it. The law states:
\(\displaystyle \oint \vec{B} \cdot d\vec{l} = \mu_0 I_{enc} \)
- (\(\displaystyle\vec{B} \)) is the magnetic field.
- (\(\displaystyle d\vec{l}\) ) is a small element of the loop.
- (µ0) is the permeability of free space.
- (Ienc) is the current enclosed by the loop.
We choose an imaginary circular loop inside the toroid, concentric with the doughnut shape. This loop is at a distance (r) from the center of the toroid.
Due to the symmetry of the toroid, the magnetic field (B) at every point on our chosen loop is the same and is directed along the loop. This means we can take (B) outside the integral:
\(\displaystyle B \oint d\vec{l} = B(2\pi r) \)
If the toroid has (N) turns and the current flowing through each turn is (I), then the total current enclosed by our loop is (NI) because the loop encircles all (N) turns.
Now we apply Ampere’s Law:
\(\displaystyle B(2\pi r) = \mu_0 NI \)
Finally, we solve for (B) to find the magnetic field inside the toroid:
\(\displaystyle B = \frac{\mu_0 NI}{2\pi r} \)
This is the expression for the magnetic field inside a toroid. It tells us that the magnetic field is directly proportional to the number of turns and the current, and inversely proportional to the radius of the loop we chose inside the toroid.
This derivation shows how the shape of the toroid and the current flowing through it work together to create a magnetic field that’s uniform and confined within the body of the toroid.
Uniform Field: Inside the toroid, the magnetic field is uniform. This means that at every point inside the toroid, the strength of the magnetic field is the same.
Outside the Toroid: Outside the toroid, the magnetic field is essentially zero. This is because the net current outside the toroid is zero, so the magnetic field cancels itself out.
Inductance of a Toroid
Inductance of a Toroid with a Rectangular Cross-Section
A toroid is like a solenoid that’s been bent into a circle. It has a core with a rectangular cross-section, and it’s wrapped with a coil of wire. The inner radius of the toroid is (a), the outer radius is (b), and the height of the core is (h).
When a current (I) flows through the wire, it creates a magnetic field inside the toroid. According to Ampere’s Law, the magnetic field (B) inside the toroid can be given by:
\(\displaystyle B = \frac{\mu_0 N I}{2\pi r} \)
where (r) is the distance from the center to the point where we’re measuring the field, (N) is the total number of turns, and (µ0) is the permeability of free space.
The magnetic flux (Φ) through one turn of the toroid is the product of the magnetic field and the area (A) of the cross-section:
\(\displaystyle \Phi = B \cdot A \)
Since the cross-section is rectangular, (\(\displaystyle A = h \cdot dr \)), where (dr) is a small change in radius.
To find the total magnetic flux linked with all (N) turns, we integrate the magnetic flux over the cross-sectional area from (a) to (b):
\(\displaystyle \Phi_{total} = N \int_a^b B \cdot h \cdot dr \)
The inductance (L) is the ratio of the total magnetic flux to the current:
\(\displaystyle L = \frac{\Phi_{total}}{I} \)
Substituting the expression for (B) from Ampere’s Law, we get:
\(\displaystyle L = \frac{N^2 \mu_0 h}{2\pi} \int_a^b \frac{dr}{r} \)
This integral is the natural logarithm of (b/a):
\(\displaystyle L = \frac{N^2 \mu_0 h}{2\pi} \ln\left(\frac{b}{a}\right) \)
This is the expression for the inductance of a toroid with a rectangular cross-section. It shows that the inductance depends on the number of turns squared, the permeability of free space, the height of the core, and the natural logarithm of the ratio of the outer radius to the inner radius.
Energy Stored in a Toroid:
The energy stored in any inductor, including a toroid, is associated with the magnetic field produced by the current flowing through the inductor. We know that the inductance (L) of a toroid can be calculated using the formula we derived earlier. For a toroid with a rectangular cross-section, it is:
\(\displaystyle L = \frac{\mu_0 \mu_r N^2 h}{2\pi} \ln\left(\frac{b}{a}\right) \)
The energy (U) stored in any inductor is given by the formula:
\(\displaystyle U = \frac{1}{2} L I^2 \)
where ( I ) is the current flowing through the inductor.
Now, we substitute our expression for (L) into the energy formula:
\(\displaystyle U = \frac{1}{2} \left(\frac{\mu_0 \mu_r N^2 h}{2\pi} \ln\left(\frac{b}{a}\right)\right) I^2 \)
To simplify, we can multiply out the constants and the current squared:
\(\displaystyle U = \frac{\mu_0 \mu_r N^2 h I^2}{4\pi} \ln\left(\frac{b}{a}\right) \)
This is the expression for the energy stored in a toroid with a rectangular cross-section. It shows that the energy depends on the permeability of free space, the relative permeability of the core material, the number of turns squared, the height of the core, the current squared, and the natural logarithm of the ratio of the outer radius to the inner radius.
Difference between Solenoid and Toroid
Both solenoids and toroids are electromagnetic devices used in various applications, but they have distinct shapes and functionalities. While solenoids are typically linear coils of wire wound in a helical shape, toroids are donut-shaped coils of wire wound in a circular or toroidal shape.
| Solenoid | Toroid |
|---|---|
| A solenoid is a coil of wire wound in a cylindrical shape with a large length-to-diameter ratio | A toroid is a coil of wire wound in a circular (doughnut) shape with a ring-shaped core |
| A solenoid produces a magnetic field outside it, which is uniform and parallel to its axis inside it | A toroid produces a magnetic field within itself, which is constant in magnitude and clockwise along the circular turn inside it |
| A solenoid has a finite length and two ends, where the magnetic field lines emerge and enter | A toroid has no ends and forms a closed loop, where the magnetic field lines are confined within the core and the coil |
| A solenoid can generate a strong magnetic field with a small number of turns and a large current | A toroid can generate a strong magnetic field with a large number of turns and a small current |
| A solenoid can cause electromagnetic interference with other devices due to its external magnetic field | A toroid can reduce electromagnetic interference with other devices due to its internal magnetic field |
| The formula for the magnetic field inside a solenoid is: \(\displaystyle B = \mu_0 nI\) | The formula for the magnetic field inside a toroid is: \(\displaystyle B = \frac{\mu_0 NI}{2 \pi r}\) |
Similarities between Solenoid and Toroid
Both solenoids and toroids operate on the principle of electromagnetism, acting as magnets when electricity passes through them. They both generate a magnetic field whose magnitude is determined by the current and the number of turns in the coil.
Based on Electromagnetism: Both solenoids and toroids operate on the principles of electromagnetism. When an electric current passes through the coils of a solenoid or a toroid, it generates a magnetic field.
Act as Electromagnets: When subjected to electricity, both solenoids and toroids act as magnets. This means they can attract ferromagnetic materials like iron, nickel, and cobalt when the current is flowing.
Magnetic Field Generation: The magnetic fields produced by both solenoids and toroids are determined by the same factors: the number of turns in the coil, the current passing through the coil, and the permeability of the core material.
Use of Coils: Both devices consist of coils of wire. In a solenoid, the wire is wound in a helical shape, while in a toroid, the wire is wound around a donut-shaped core.
Right-Hand Thumb Rule: The direction of the magnetic field in both solenoids and toroids can be determined using the right-hand thumb rule. If you point your thumb in the direction of the current, your fingers will curl in the direction of the magnetic field.
Solenoids and toroids are used in various applications where controlled magnetic fields are required, such as in electrical relays, transformers, inductors, and motors.
Applications of Toroid
Inductors: Toroids are commonly used as low-level inductors in circuits. Their ability to contain the magnetic field within the core makes them efficient for this purpose. They help in storing energy in the form of a magnetic field when electrical current flows through them.
Transformers: In power supplies, toroids serve as power transformers. They step up or step down voltage levels efficiently, which is crucial in various electronic devices and electrical systems.
Current Transformers: Toroids are used in current transformers, which are designed to provide a current in its secondary coil proportional to the current flowing in its primary coil. This is essential for current measurement and control.
Telecommunication: In the field of telecommunication, toroids are used to prevent interference from other devices and signals. They ensure that communication signals are clear and undisturbed.
Medical Equipment: Modern medical equipment often includes toroids. They are used in devices where precise control of magnetic fields is necessary, such as in MRI machines.
Musical Instruments: The design of some musical instruments incorporates toroids. They can be used to shape the tone and reduce electrical noise in electronic instruments.
Also Read: Solenoid
Solved Examples
Problem 1: A toroid has 2000 turns, a mean radius of 0.1 m, and a current of 5 A. Calculate the magnetic field inside the toroid.
Solution: The magnetic field inside a toroid is given by:
\(\displaystyle B = \frac{\mu_0 N I}{2\pi r} \)
Given: (N = 2000), (I = 5 A), (r = 0.1 m)
\(\displaystyle B = \frac{4\pi \times 10^{-7} \times 2000 \times 5}{2\pi \times 0.1} \)
\(\displaystyle B = \frac{4\pi \times 10^{-7} \times 10000}{2\pi \times 0.1} \)
\(\displaystyle B = \frac{4 \times 10^{-3}}{0.1} \)
\(\displaystyle B = 4 \times 10^{-2} \, \text{T} \)
The magnetic field inside the toroid is (\(\displaystyle 4 \times 10^{-2} \, \text{T} \)).
Problem 2: A toroid has a mean radius of 0.2 m, 1500 turns, and a cross-sectional area of ( 0.01 m2). Calculate the inductance of the toroid.
Solution: The inductance (L) of a toroid is given by:
\(\displaystyle L = \frac{\mu_0 N^2 A}{2\pi r} \)
Given: (N = 1500), ( A = 0.01 m2), (r = 0.2 m)
\(\displaystyle L = \frac{4\pi \times 10^{-7} \times 1500^2 \times 0.01}{2\pi \times 0.2} \)
\(\displaystyle L = \frac{4 \times 10^{-7} \times 2250000 \times 0.01}{0.4} \)
\(\displaystyle L = \frac{9 \times 10^{-3}}{0.4} \)
\(\displaystyle L = 2.25 \times 10^{-2} \, \text{H} \)
The inductance of the toroid is (\(\displaystyle 2.25 \times 10^{-2} \, \text{H} \)).
Problem 3: A toroid has a mean radius of 0.15 m and a minor radius of 0.03 m. Calculate the volume and surface area of the toroid.
Solution: The volume (V) of a toroid is given by:
\(\displaystyle V = 2\pi^2 r_{\text{mean}} r_{\text{minor}}^2 \)
The surface area (A) of a toroid is given by:
\(\displaystyle A = 4\pi^2 r_{\text{mean}} r_{\text{minor}} \)
Given: (\(\displaystyle r_{\text{mean}} = 0.15 \, \text{m} \)), (\(\displaystyle r_{\text{minor}} = 0.03 \, \text{m} \))
Volume:
\(\displaystyle V = 2\pi^2 \times 0.15 \times (0.03)^2 \)
\(\displaystyle V = 2\pi^2 \times 0.15 \times 0.0009 \)
\(\displaystyle V = 2\pi^2 \times 0.000135 \)
\(\displaystyle V \approx 2.67 \times 10^{-3} \, \text{m}^3\)
Surface Area:
\(\displaystyle A = 4\pi^2 \times 0.15 \times 0.03 \)
\(\displaystyle A = 4\pi^2 \times 0.0045 \)
\(\displaystyle A \approx 0.178 \, \text{m}^2 \)
The volume of the toroid is (\(\displaystyle 2.67 \times 10^{-3} \, \text{m}^3 \)) and the surface area is (\(\displaystyle 0.178 \, \text{m}^2 \)).
Problem 4: A toroidal coil has a mean radius of 0.1 m, a magnetic field of (0.05 T), and carries a current of (4 A). Calculate the number of turns in the coil.
Solution: The magnetic field inside a toroid is given by:
\(\displaystyle B = \frac{\mu_0 N I}{2\pi r} \)
Rearranging for (N):
\(\displaystyle N = \frac{B \cdot 2\pi r}{\mu_0 I} \)
Given: (B = 0.05 T), (r = 0.1 m), (I = 4 A)
\(\displaystyle N = \frac{0.05 \times 2\pi \times 0.1}{4\pi \times 10^{-7} \times 4} \)
\(\displaystyle N = \frac{0.05 \times 0.2}{1.6 \times 10^{-6}} \)
\(\displaystyle N = \frac{0.01}{1.6 \times 10^{-6}} \)
\(\displaystyle N \approx 6250 \)
Answer: The number of turns in the toroidal coil is approximately 6250.
Problem 5: A toroid has a mean radius of 0.1 m, a cross-sectional area of (0.01 m2), 1500 turns, and carries a current of (6 A). Calculate the energy stored in the magnetic field of the toroid.
Solution: The energy stored in the magnetic field of a toroid is given by:
\(\displaystyle U = \frac{1}{2} L I^2 \)
Where: \(\displaystyle L = \frac{\mu_0 N^2 A}{2\pi r} \)
Given: (N = 1500), (A = 0.01 m2), (r = 0.1 m), (I = 6 A)
First, calculate the inductance (L):
\(\displaystyle L = \frac{4\pi \times 10^{-7} \times 1500^2 \times 0.01}{2\pi \times 0.1} \)
\(\displaystyle L = \frac{4 \times 10^{-7} \times 2250000 \times 0.01}{0.2} \)
\(\displaystyle L = 4.5 \times 10^{-3} \, \text{H} \)
Now, calculate the energy stored:
\(\displaystyle U = \frac{1}{2} \times 4.5 \times 10^{-3} \times 6^2 \)
\(\displaystyle U = \frac{1}{2} \times 4.5 \times 10^{-3} \times 36 \)
\(\displaystyle U = 0.081 \, \text{J} \)
The energy stored in the magnetic field of the toroid is (0.081 J).
FAQs
What is a toroid and how is it constructed?
A toroid is a doughnut-shaped coil of wire that is used to generate a magnetic field. It is constructed by winding a long wire into a helical shape around a ring-shaped core, typically made of ferromagnetic material, to form a closed loop.
How does a toroid produce a magnetic field?
A toroid produces a magnetic field when an electric current flows through its coils. The current generates magnetic fields around each turn of the wire, which combine to produce a strong, continuous magnetic field confined within the core of the toroid, circulating along the circular path.
What are the advantages of using a toroid over a solenoid?
The advantages of using a toroid over a solenoid include better containment of the magnetic field, reducing electromagnetic interference with nearby electronic components, and a more efficient use of space. The closed-loop shape of a toroid minimizes the external magnetic field, making it ideal for applications where stray magnetic fields could be problematic.
What are some common applications of toroids?
Common applications of toroids include their use in transformers, inductors, chokes, and sensors. They are also used in electronic circuits to filter signals, in power supplies to smooth out current, and in communication devices to reduce electromagnetic interference.
Why is the magnetic field inside a toroid confined within its core?
The magnetic field inside a toroid is confined within its core due to the closed-loop geometry of the coil. This shape ensures that the magnetic field lines are continuous and loop back on themselves within the core, minimizing any external magnetic field. This containment is due to the fact that the magnetic field outside the toroid cancels out, resulting in a negligible external field.
How does the core material affect the magnetic field of a toroid?
The core material of a toroid affects its magnetic field by influencing the magnetic permeability of the toroid. A core made of a ferromagnetic material, such as iron, significantly enhances the magnetic field within the toroid by allowing a greater concentration of magnetic field lines, compared to a non-magnetic or air core.
What factors influence the inductance of a toroid?
The inductance of a toroid is influenced by several factors, including the number of turns of the wire, the cross-sectional area of the core, the length of the toroid, and the magnetic permeability of the core material. Increasing the number of turns, using a core with a larger cross-sectional area, or using a material with higher magnetic permeability will all increase the inductance of the toroid.