The story of bar magnets begins with the discovery of lodestones, naturally magnetized pieces of the mineral magnetite, which were used by ancient civilizations for navigation. The term “magnet” comes from Magnesia, a region in modern-day Turkey, where lodestones were found in abundance.
In China around 1000 CE, magnetized iron bars, known as lodestones, were observed to align themselves north-south when floated in bowls of water. This was one of the earliest uses of magnetic materials for navigation.
The scientific study of magnetism started to gain momentum in the 1600s. Petrus Peregrinus de Maricourt wrote about the properties of magnets around 1269, and William Gilbert published his seminal work, “De Magnete,” in 1600. Gilbert’s work described the first systematic experiments with magnetism and established that the Earth itself behaved like a giant magnet.
Bar magnets, as we know them today, are man-made magnets that come in the shape of a bar and have two poles: north and south. If you cut a bar magnet in half, you don’t get a single north or south pole but instead, two smaller bar magnets, each with its own north and south poles. This is because the magnetic monopoles do not exist independently; they always come in pairs.
What is a Bar Magnet?
A bar magnet is a rectangular object that generates a magnetic field due to the alignment of magnetic domains within it. Imagine you have a bar-shaped object, typically made of iron, steel, or any ferromagnetic material. This object is not just any ordinary bar; it has a superpower: it can attract certain metals and also interact with other magnets. This special bar is what we call a bar magnet.
A bar magnet has two ends, each called a pole. One end is the North Pole, and the other is the South Pole. These poles are where the magnet’s invisible force, known as the magnetic field, is strongest. If you were to hang a bar magnet on a string, it would rotate until the North Pole points towards the Earth’s North Magnetic Pole, which is magnetic south (yes, it’s a bit confusing, but that’s how magnets work!).
Now, you might wonder, what makes this bar a magnet? Inside the bar, there are countless tiny regions called domains. Each domain is like a mini magnet with its own North and South Poles. In most objects, these domains are all jumbled up, pointing in random directions, so their magnetic fields cancel each other out. But in a bar magnet, most of these domains are aligned in the same direction, which gives the bar its magnetic properties.
If you cut a bar magnet in half, you don’t get a separate North and South Pole; instead, you get two smaller bar magnets, each with its own North and South Poles. This is because magnetic poles always come in pairs—there’s no such thing as a solo North or South Pole in nature.
So, a bar magnet is essentially a bar that has aligned magnetic domains, resulting in a magnetic field with distinct North and South Poles. It’s this field that allows the magnet to attract or repel other magnetic materials and also to interact with the Earth’s magnetic field.
Types of Bar Magnet
When we talk about bar magnets, we’re referring to magnets that have a simple, elongated shape. But even within this category, there are a couple of different types that have their own unique characteristics. Let’s take a look at them:
Cylindrical Bar Magnet: Imagine a long, round stick made of metal that can stick to your fridge or pick up paper clips. That’s a cylindrical bar magnet. It’s like a metal rod with magnetic powers. These magnets are often used in science experiments at school because they have a uniform magnetic field along their length, which makes them great for demonstrating how magnets work.
Rectangular Bar Magnet: Now, picture a block of metal, like a small brick, that can also stick to your fridge or hold up your shopping list. This is a rectangular bar magnet. It’s shaped like a box or a brick and is the type you might have played with in science class. These magnets are strong and easy to handle, which is why they’re used in many industrial applications. They have a strong magnetic field and are good at picking up other metal objects.
Both types of bar magnets have the same basic properties: they have a North Pole and a South Pole, and they can attract or repel other magnets. The difference mainly lies in their shape and the strength of their magnetic field, which is determined by the material they’re made of and their size.
So, whether it’s a cylindrical bar magnet or a rectangular one, the magic of magnetism works in the same fascinating way. These magnets are super useful, not just in our science classes but also in the real world, where they help in all sorts of devices, from speakers to electric motors!
Properties of Bar Magnet
A bar magnet isn’t just a piece of metal; it’s a fascinating object with some pretty cool features. Here are the key properties that make bar magnets special:
Magnetic Poles: Every bar magnet has two ends, known as poles. One is the North Pole, and the other is the South Pole. These aren’t just random spots; they’re the areas where the magnet’s invisible force, the magnetic field, is the strongest.
Inseparable Poles: If you think you can separate the North and South Poles by cutting a bar magnet in half, think again! No matter how many times you slice it, each piece will always have a North and a South Pole. It’s like trying to separate the two ends of a stick – no matter how small the pieces, each will always have two ends.
Directional Property: A bar magnet is like a compass needle. If you suspend it freely, it will swing around until it lines up with the Earth’s magnetic field, pointing geographically north-south. This is why magnets were so important for navigation before GPS came along.
Attraction and Repulsion: Magnets are social creatures – they love to interact. A bar magnet will pull towards any ferromagnetic material, like iron, nickel, or cobalt. But when it comes to other magnets, they’re picky. Opposite poles attract each other, while like poles push each other away. It’s the classic case of opposites attract.
Magnetic Field Lines: If you could see a magnet’s magnetic field, it would look like a series of lines looping from the North Pole to the South Pole. These lines are a map of the magnet’s influence, showing how and where it will affect other magnetic objects.
Strength at the Poles: The magnetic force isn’t spread out evenly. It’s strongest at the poles and gets weaker as you move towards the center of the magnet. This is why the ends of a bar magnet are great for picking up paper clips, while the middle, is not so much.
Magnetic Field Lines Around Bar Magnet
Imagine you could see the invisible force field around a bar magnet. What you’d see would look like a series of loops emerging from one end of the magnet and curving around to re-enter at the other end. These loops are what we call magnetic field lines.

The field lines emerge from the North Pole of the magnet, which is the end that points towards the geographic North Pole of the Earth. They then arc through the air, creating a loop, and enter the South Pole of the magnet, which is the end that points towards the geographic South Pole of the Earth.
Inside the magnet, these lines continue from the South Pole back to the North Pole, completing the loop. These field lines are not just theoretical; they represent the direction and strength of the magnetic field. If you placed a compass near a bar magnet, the compass needle would align with these field lines, showing you the direction of the magnetic field at that point.
- They never cross each other because that would mean there are two directions of the magnetic field at one point, which is impossible.
- The density of the lines indicates the strength of the magnetic field: more lines per unit area mean a stronger magnetic field.
- The lines are closer together at the poles, where the magnetic field is strongest, and spread out as they move away from the magnet.
To visualize this, you can do a simple experiment with iron filings and a bar magnet. Sprinkle the filings around the magnet, and you’ll see them align along the field lines, creating a pattern that shows the magnetic field’s shape.
Pole Strength of Bar Magnet
Imagine you have a bar magnet, and you bring it close to a pile of iron filings. The filings jump up and cling to the ends of the magnet, right? That’s the magnet’s poles at work. The pole strength is like the magnet’s “muscle power” at each pole – it’s what pulls those filings in and holds them tight.
The pole strength of a bar magnet is a measure of how strongly the magnet can attract or repel other magnetic materials. It’s a bit like measuring the strength of a person by how much weight they can lift. Here’s what you need to know: Pole strength (P) is the measure of the magnetic power at the magnet’s pole. It tells us how strong the pull (or push) is when another magnetic material comes close to the magnet’s pole.
Work done (W) is the energy required to move a magnet around a wire carrying an electric current. It’s like the effort you put in to move something from one place to another. Electric current (I) is the flow of electric charge through the wire. The interaction between the moving magnet and the current creates a magnetic field.
\(\displaystyle P = \frac{W}{I} \)
It says that the pole strength is equal to the work done divided by the electric current. In other words, it’s a way to calculate how strong the magnet’s pole is based on the work done by the electric current³.
SI Unit: The standard unit of pole strength is Newton per Tesla (N/T), which combines the units of force (Newtons) and magnetic field strength (Tesla).
Magnetic Field of a Bar Magnet
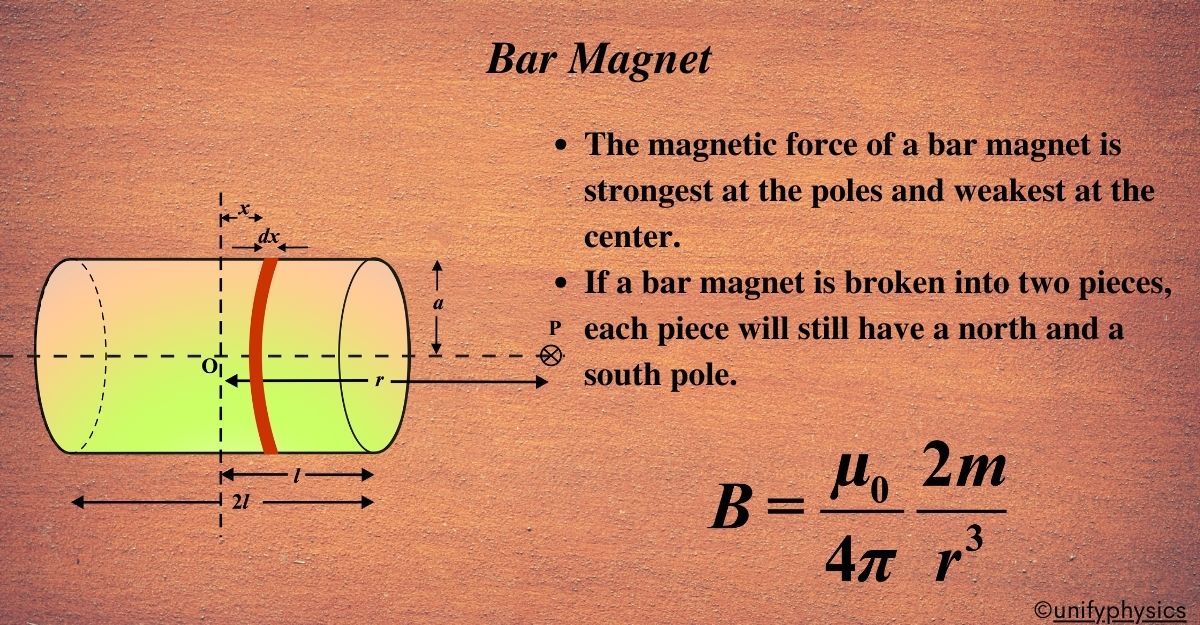
A bar magnet has two poles, North (N) and South (S), and the magnetic field lines emerge from the North pole and enter the South pole. To derive the magnetic field at a point on the axial line, we consider the following:
- Pole Strength (m): This is the strength of each pole of the bar magnet.
- Distance (r): The distance from the center of the magnet to the point where we want to calculate the magnetic field.
- Length of the Magnet (2l): The distance between the two poles of the bar magnet.
The magnetic field (B) at a distance (r) from a single magnetic pole of strength (m) in a medium with permeability (µ0) is given by:
\(\displaystyle B = \frac{\mu_0}{4\pi} \frac{m}{r^2} \)
At a point along the axial line of the bar magnet, the magnetic field due to the North pole is directed away from the magnet, and the magnetic field due to the South pole is directed toward the magnet.
The net magnetic field at point (P) on the axial line is the difference between the fields due to the North and South poles because they are in opposite directions. If (d) is the distance from the midpoint of the magnet to point (P), the net field is:
\(\displaystyle B = \frac{\mu_0}{4\pi} \left( \frac{m}{(d – l)^2} – \frac{m}{(d + l)^2} \right) \)
We can simplify the above expression by finding a common denominator and subtracting the two fractions:
\(\displaystyle B = \frac{\mu_0}{4\pi} \frac{m[(d + l)^2 – (d – l)^2]}{(d^2 – l^2)^2} \)
\(\displaystyle B = \frac{\mu_0}{4\pi} \frac{m[4dl]}{(d^2 – l^2)^2} \)
\(\displaystyle B = \frac{\mu_0}{4\pi} \frac{4mdl}{(d^2 – l^2)^2} \)
The final expression for the magnetic field at a point on the axial line of a bar magnet is:
\(\displaystyle B = \frac{\mu_0}{4\pi} \frac{2m}{r^3} \)
where (r) is the distance from the pole to the point (P), and we assume (r) is much larger than (l), so (\(\displaystyle r \approx d \)). This expression shows that the magnetic field decreases with the cube of the distance from the pole and is directly proportional to the pole strength of the magnet.
Bar Magnet as an Equivalent Solenoid
A bar magnet is a piece of material, usually made of iron, steel, or another ferromagnetic substance, that has a magnetic field around it. It has two poles: a North pole and a South pole. The magnetic field lines emerge from the North pole and loop around to enter the South pole.
A solenoid is a coil of wire that, when carrying an electric current, produces a magnetic field. The field inside the solenoid is very similar to the field of a bar magnet, with field lines running parallel inside the coil.
The idea here is that a bar magnet can be thought of as having an equivalent solenoid wrapped around it. This is because the magnetic field produced by a solenoid with current flowing through it can be very similar to the magnetic field around a bar magnet.
A solenoid is a coil of wire that produces a magnetic field when an electric current passes through it. The strength of the magnetic field inside a solenoid is given by:
\(\displaystyle B_{\text{solenoid}} = \mu_0 n I \)
- (µ0) is the permeability of free space,
- (n) is the number of turns per unit length of the solenoid,
- (I) is the current flowing through the solenoid.
The magnetic moment (M) of a solenoid is the product of the current (I), the number of turns (N), and the area of the coil (A):
M = NIA
The magnetic field (B) at a point along the axis of a bar magnet, at a distance (r) from its center, is given by:
\(\displaystyle B = \frac{\mu_0}{4\pi} \frac{2M}{r^3} \)
where ( M ) is the magnetic moment of the bar magnet.
For a bar magnet to be equivalent to a solenoid, their magnetic moments must be equal. This means:
\(\displaystyle M_{\text{solenoid}} = M_{\text{bar magnet}} \)
\(\displaystyle NIA = m \times (2l) \)
where (m) is the pole strength of the bar magnet and (2l) is the distance between the poles. Using the relationship between the magnetic moment and the magnetic field, we can write the magnetic field of the bar magnet in terms of the magnetic moment of the equivalent solenoid:
\(\displaystyle B = \frac{\mu_0}{4\pi} \frac{2(NIA)}{r^3} \)
\(\displaystyle B = \frac{\mu_0}{4\pi} \frac{2m(2l)}{r^3} \)
\(\displaystyle B = \frac{\mu_0}{4\pi} \frac{4ml}{r^3} \)
The derived expression shows that the magnetic field of a bar magnet can be modeled using the same principles that describe the magnetic field of a solenoid, with the magnetic moment being the key linking factor.
The expected result for the magnetic field (B) of a bar magnet treated as an equivalent solenoid is:
\(\displaystyle B = \frac{\mu_0}{4\pi} \frac{2m}{r^3} \)
where (m) is the magnetic moment of the bar magnet, (r) is the distance from the center of the magnet to the point where the magnetic field is being measured, and (µ0) is the permeability of free space. This formula indicates that the magnetic field decreases with the cube of the distance from the magnet and is directly proportional to the magnetic moment of the magnet.
Difference between Bar Magnet and Electromagnet
| Feature | Bar Magnet | Electromagnet |
|---|---|---|
| Nature | Permanent magnet | Temporary magnet |
| Magnetism Source | The magnetic field can be turned on and off | Generated by an electric current passing through a coil of wire. |
| Magnetic Field | Constant magnetic field | Used in compasses, fridge magnets, and motors where constant magnetism is needed |
| Polarity | Fixed North and South poles | Poles can be reversed by changing the direction of the current |
| Strength | Generally weaker compared to an electromagnet | Can be very strong; strength can be adjusted by changing the current |
| Durability | Retains magnetism over time | Only magnetic when current is flowing |
| Applications | Used in compasses, fridge magnets, and in motors where constant magnetism is needed | Used in cranes for lifting heavy metal objects, in MRI machines, and as switches in electronic devices |
Alnico and Neodymium Bar Magnets
Alnico Bar Magnets: Alnico magnets are made from an alloy of aluminum, nickel, and cobalt. They were some of the first materials to be used for permanent magnets. Here’s what makes them special:
- Temperature Stability: Alnico magnets have excellent temperature stability and can be used at very high temperatures.
- Magnetic Strength: While they have good magnetic strength, they are generally weaker than neodymium magnets.
- Resistance to Demagnetization: They have a good resistance to demagnetization, which means they maintain their magnetism well over time.
- Applications: Alnico magnets are commonly used in electric motors, microphones, sensors, and loudspeakers.
Neodymium Bar Magnets: Neodymium magnets, on the other hand, are made from an alloy of neodymium, iron, and boron. They are part of the rare-earth magnet family and are known for:
- Incredible Strength: Neodymium magnets are the strongest type of permanent magnets available today.
- Temperature Sensitivity: They are less temperature stable than Alnico and can lose magnetism at high temperatures.
- High Resistance to Demagnetization: Neodymium magnets have a very high resistance to demagnetization.
- Applications: They are used in various applications requiring strong magnetic fields, such as in computer hard drives, magnetic fasteners, and jewelry clasps.
Both Alnico and Neodymium magnets have their unique advantages and are chosen based on the specific requirements of the application. Alnico is preferred for its temperature stability and resistance to demagnetization, while Neodymium is chosen for its exceptional strength and compact size.
Applications of Bar Magnets
Educational Tools: Bar magnets are commonly used in classrooms to demonstrate the properties of magnetism, including attraction, repulsion, and the magnetic field lines that emerge from the North Pole and enter the South Pole.
Industrial Uses: In industries, bar magnets are used to separate metallic impurities from materials. They are also used in magnetic cranes to lift heavy iron loads.
Electronic Devices: Small bar magnets are found in electronic devices like speakers, telephones, and computer hard drives, where they are used to convert electrical energy into mechanical energy (sound) or to store data.
Medical Field: Bar magnets have applications in medical equipment, such as in Magnetic Resonance Imaging (MRI) machines, which use powerful magnets to create images of the body’s interior.
Everyday Objects: You’ll find bar magnets in everyday items like refrigerator magnets, cabinet latches, and toys.
Scientific Research: In research laboratories, bar magnets are used in various experiments to study magnetic fields and forces.
These are just a few examples of how bar magnets are applied in different fields. Their use is widespread due to their ability to create a consistent magnetic field, which can be harnessed for various purposes.
Also Read: Solenoid
Solved Examples
Problem 1: A bar magnet has a length of (10 cm) and a magnetic moment of (2A m2). Calculate the magnetic field at a point (20 cm) from the center of the magnet along its axis.
Solution: The magnetic field (B) at a distance (x) from the center of a bar magnet along its axial line is given by:
\(\displaystyle B = \frac{\mu_0}{4\pi} \cdot \frac{2M}{(x^2 – l^2)^2} \)
Given: \(\displaystyle 2l = 10 \, \text{cm} = 0.1 \, \text{m}\) ), hence (l = 0.05 m); \(\displaystyle M = 2 \, \text{A} \cdot \text{m}^2 \); \(\displaystyle x = 20 \, \text{cm} = 0.2 \, \text{m} \)
\(\displaystyle B = \frac{4\pi \times 10^{-7}}{4\pi} \cdot \frac{2 \times 2}{(0.2^2 – 0.05^2)^{2}} \)
\(\displaystyle B = 10^{-7} \cdot \frac{4}{(0.04 – 0.0025)^{2}} \)
\(\displaystyle B = 10^{-7} \cdot \frac{4}{(0.0375)^{2}} \)
\(\displaystyle B = 10^{-7} \cdot \frac{4}{0.00140625} \)
\(\displaystyle B \approx 10^{-7} \cdot 2844.44 \)
\(\displaystyle B \approx 2.84 \times 10^{-4} \, \text{T} \)
The magnetic field at (20 cm) from the center of the magnet along its axis is (\(\displaystyle 2.84 \times 10^{-4} \, \text{T}\) ).
Problem 2: A bar magnet has a magnetic moment of (\(\displaystyle 3 \, \text{A} \cdot \text{m}^2 \)) and a length of (8cm). Calculate the magnetic field at a point (10 cm) from the center of the magnet on the equatorial line.
Solution: The magnetic field (B) at a distance (x) from the center of a bar magnet along its equatorial line is given by:
\(\displaystyle B = \frac{\mu_0}{4\pi} \cdot \frac{M}{(x^2 + l^2)^{3/2}} \)
Given: \(\displaystyle 2l = 8 \, \text{cm} = 0.08 \, \text{m} \), hence ( l = 0.04 \, \text{m} ); \(\displaystyle M = 3 \, \text{A} \cdot \text{m}^2 \); x = 10 cm = 0.1 m)
\(\displaystyle B = \frac{4\pi \times 10^{-7}}{4\pi} \cdot \frac{3}{(0.1^2 + 0.04^2)^{3/2}} \)
\(\displaystyle B = 10^{-7} \cdot \frac{3}{(0.01 + 0.0016)^{3/2}} \)
\(\displaystyle B = 10^{-7} \cdot \frac{3}{0.0116^{3/2}} \)
\(\displaystyle B = 10^{-7} \cdot \frac{3}{0.001247} \)
\(\displaystyle B \approx 10^{-7} \cdot 2404.82 \)
\(\displaystyle B \approx 2.40 \times 10^{-4} \, \text{T} \)
The magnetic field at (10 cm) from the center of the magnet on the equatorial line is (\(\displaystyle 2.40 \times 10^{-4} \, \text{T}\) ).
Problem 3: Two magnetic poles, each of pole strength (\(\displaystyle 10 \, \text{A} \cdot \text{m} \)), are separated by a distance of (5 cm). Calculate the force between them if they are in a vacuum.
Solution: The force (F) between two magnetic poles is given by:
\(\displaystyle F = \frac{\mu_0}{4\pi} \cdot \frac{m_1 m_2}{d^2} \)
Given: m1 = m2 = 10 A∙m; d = 5 cm = 0.05 m
\(\displaystyle F = \frac{4\pi \times 10^{-7}}{4\pi} \cdot \frac{10 \times 10}{0.05^2} \)
\(\displaystyle F = 10^{-7} \cdot \frac{100}{0.0025} \)
\(\displaystyle F = 10^{-7} \cdot 40000 \)
\(\displaystyle F = 4 \times 10^{-3} \, \text{N} \)
The force between the two magnetic poles is (\(\displaystyle 4 \times 10^{-3} \, \text{N} \)).
Problem 4: A bar magnet has a pole strength of (\(\displaystyle 20 \, \text{A} \cdot \text{m}\) ) and a length of (12 cm). Calculate the magnetic dipole moment of the bar magnet.
Solution: The magnetic dipole moment (M) of a bar magnet is given by:
\(\displaystyle M = m \times 2l \)
Given: m = 20 A∙m ; \(\displaystyle 2l = 12 \, \text{cm} = 0.12 \, \text{m} \)
\(\displaystyle M = 20 \times 0.12 \)
\(\displaystyle M = 2.4 \, \text{A} \cdot \text{m}^2 \)
The magnetic dipole moment of the bar magnet is (\(\displaystyle 2.4 \, \text{A} \cdot \text{m}^2 \)).
Problem 5: A bar magnet has a length of (8 cm) and a magnetic moment of (\(\displaystyle 5 \, \text{A} \cdot \text{m}^2 \)). Calculate the magnetic field at a point (4 cm) from the center of the magnet on the axial line.
Solution: The magnetic field (B) at a distance (x) from the center of a bar magnet along its axial line is given by:
\(\displaystyle B = \frac{\mu_0}{4\pi} \cdot \frac{2M}{(x^2 – l^2)^2}\)
\(\displaystyle B = \frac{4\pi \times 10^{-7}}{4\pi} \cdot \frac{2 \times 5}{(0.04^2 – 0.04^2)^{2}} \)
\(\displaystyle B = 10^{-7} \cdot \frac{10}{0} \)
The magnetic field at this point is undefined because (x = l), which makes the denominator zero.
The magnetic field at (4 cm) from the center of the magnet on the axial line is undefined due to the distance being equal to half the length of the magnet.
Problem 6: A bar magnet with a magnetic moment of (\(\displaystyle 1.5 \, \text{A} \cdot \text{m}^2 \)) has a length of (6 cm). Calculate the magnetic field at a point (15 cm) from the center of the magnet along its axis.
Solution: The magnetic field (B) at a distance (x) from the center of a bar magnet along its axial line is given by:
\(\displaystyle B = \frac{\mu_0}{4\pi} \cdot \frac{2M}{(x^2 – l^2)^2} \)
\(\displaystyle B = \frac{4\pi \times 10^{-7}}{4\pi} \cdot \frac{2 \times 1.5}{(0.15^2 – 0.03^2)^{2}} \)
\(\displaystyle B = 10^{-7} \cdot \frac{3}{(0.0225 – 0.0009)^{2}} \)
\(\displaystyle B = 10^{-7} \cdot \frac{3}{0.0216^{2}} \)
\(\displaystyle B = 10^{-7} \cdot \frac{3}{0.00046656} \)
\(\displaystyle B \approx 10^{-7} \cdot 6429.32 \)
\(\displaystyle B \approx 6.43 \times 10^{-4} \, \text{T} \)
The magnetic field at (15 cm) from the center of the magnet along its axis is (\(\displaystyle 6.43 \times 10^{-4} \, \text{T} \)).
FAQs
What is a bar magnet?
A bar magnet is a rectangular piece of magnetized material that generates a magnetic field. It has two distinct poles: a north pole and a south pole, where the magnetic force is strongest.
How do the poles of a bar magnet interact with each other and other magnets?
The poles of a bar magnet interact according to the basic principle of magnetism: opposite poles attract, while like poles repel. Therefore, the north pole of one magnet will attract the south pole of another magnet and repel another north pole.
What happens when a bar magnet is cut into two pieces?
When a bar magnet is cut into two pieces, each piece becomes a smaller bar magnet with its own north and south poles. This occurs because the magnetic domains within the material reorient to maintain a north and south pole in each piece.
How does the magnetic field around a bar magnet look?
The magnetic field around a bar magnet can be visualized as lines that emerge from the north pole and curve around to enter the south pole. These lines are called magnetic field lines and they illustrate the direction and strength of the magnetic field.
What is the difference between a permanent bar magnet and an electromagnet?
A permanent bar magnet generates a constant magnetic field without the need for an external power source. An electromagnet, on the other hand, generates a magnetic field only when an electric current flows through a coil of wire wrapped around a core, typically made of iron.
How can the strength of a bar magnet be measured?
The strength of a bar magnet can be measured using a magnetometer, which measures the magnetic field intensity. Alternatively, the force it exerts on ferromagnetic materials or the deflection it causes in a compass needle can indicate its strength.
What are some common applications of bar magnets?
Bar magnets are used in a variety of applications, including in educational demonstrations, compasses, magnetic locks, and various types of sensors and electronic devices. They are also used in industrial settings for magnetic separation and holding purposes.