The story of hysteresis begins in the 19th century, but its roots stretch back to ancient times. The word “hysteresis” itself comes from an Ancient Greek word meaning “deficiency” or “lagging”. This term was chosen because it perfectly describes how certain materials react to changes not immediately, but with a delay, or lag.
In 1881, a physicist named Sir James Alfred Ewing introduced the term “hysteresis” to describe the peculiar behavior of magnetic materials. He noticed that when a magnetic field is applied to a ferromagnetic material like iron, the material’s magnetization doesn’t change instantly. Instead, it lags behind the applied magnetic field, creating a sort of “memory” of its magnetic history.
Before Ewing, other scientists like James Clerk Maxwell had also observed and described similar lagging behaviors in mechanical systems. Their work laid the foundation for understanding hysteresis in various materials and systems.
As the study of hysteresis evolved, it became clear that this phenomenon was not just limited to magnetism. It was found in many natural systems, including ferroelectric materials and even in the deformation of rubber bands. The concept of hysteresis has since been applied in physics, chemistry, engineering, biology, and even economics.
In the 1970s, a group of Russian mathematicians led by Mark Krasnosel’skii developed a more formal mathematical theory of systems with hysteresis, which helped in modeling and predicting the behavior of such systems.
Today, the history of hysteresis is a testament to the curiosity and persistence of scientists who sought to understand the complex behaviors of materials. It’s a concept that has profound implications in technology, from the memory stored on a hard disk drive to the design of electrical components that rely on magnetic properties.
What Is Hysteresis?
Hysteresis refers to the phenomenon where the state of a material lags behind the forces affecting it. In magnetism, it describes how a material’s magnetic induction (B) doesn’t instantly follow the magnetic field strength (H), especially when the field is changing.
Imagine you’re playing with a spring. You pull it, and it stretches; you release it, and it goes back to its original shape. But what if the spring didn’t return to its exact starting point right away, or it took a different path when returning? This is similar to what happens in hysteresis.
In physics, hysteresis is like the spring’s memory. It’s a phenomenon that occurs when the response of a material, like a magnet, doesn’t immediately follow the changes in the force applied to it. Instead, it shows a sort of lag or delay.
Let’s use a magnet as an example:
- You start with a piece of iron that’s not a magnet yet.
- You bring a strong magnet close to it, and slowly, the iron starts to act like a magnet too. This is because the tiny magnetic parts inside the iron, called domains, are aligning with the magnetic field.
- Now, if you remove the strong magnet, you’d expect the iron to stop being a magnet, right? But it doesn’t happen instantly. The iron retains some of its magnetism for a while. This “memory” of being a magnet, even after the external magnet is gone, is hysteresis.
In technical terms, hysteresis is the lagging of the magnetic flux density (B) behind the magnetic field strength (H). When you plot this relationship on a graph, you get a looped curve called the hysteresis loop. This loop tells us how much the material remembers its magnetic state and how much energy is lost in the process of magnetizing and demagnetizing.
So, in simple words, hysteresis is the material’s way of saying, “I remember being a magnet, and I’m going to hold onto that memory for a bit, even if you’re not making me a magnet anymore.”
Types of Hysteresis
There are two main types:
Rate-dependent hysteresis
This occurs when there’s a phase lag between an input and its output, often seen in systems with sinusoidal inputs and outputs. Imagine you’re listening to your favorite song on headphones. If you turn the volume up quickly, it takes a moment for your ears to adjust to the louder sound. This delay in response to the change in volume is similar to rate-dependent hysteresis.
In physics, rate-dependent hysteresis is all about timing and frequency. It occurs when the response of a system depends on how quickly the input changes.
Frequency: Just like certain songs sound better at different volumes, rate-dependent hysteresis is more pronounced at certain frequencies. If you change the input slowly, the system might not show much hysteresis, but if you change it quickly, the hysteresis becomes more noticeable.
Phase Lag: Think of a dance where your movements are supposed to match the beat of the music. If there’s a lag in your steps, you’re out of sync with the music. Similarly, in rate-dependent hysteresis, there’s a phase lag between the input (the music) and the output (your dance moves).
Low-Pass Filter Example: A low-pass filter in electronics is a good example of rate-dependent hysteresis. It allows low-frequency signals to pass through easily but delays the high-frequency ones, causing a phase lag. This lag isn’t the same at all frequencies; it increases as the input frequency goes up.
Imagine driving a car over different terrains. On a smooth road, you can go fast without much trouble, but on a bumpy road, you have to slow down to maintain control. The car’s suspension system shows rate-dependent hysteresis because its response (the smoothness of your ride) depends on the rate at which you’re driving over bumps (the input frequency).
So in simple terms, rate-dependent hysteresis is like a dance between input and output that’s choreographed by the frequency of changes. It’s a dynamic interaction where the system’s history of inputs and the speed of those inputs determine the current response.
Rate-independent hysteresis
Here, the system retains a memory of past inputs, even after transients have disappeared. Imagine you have a playlist of songs that you listen to every day. No matter if you play the songs fast or slow, the order of the songs doesn’t change. Similarly, rate-independent hysteresis is about the order of events, not how fast they happen.
In physics, rate-independent hysteresis means the output of a system doesn’t depend on how quickly the input changes.
Steady Memory: Think of a light switch with a dimmer. You can turn the light up or down slowly or quickly, but the brightness level you set last time is where it starts from again. The switch “remembers” the last setting, regardless of how fast you adjust it.
Consistent Response: It’s like having a favorite chair that molds to your shape. Whether you sit down quickly or slowly, the chair ends up fitting you the same way. The chair’s response (the shape it takes) is independent of how fast you sit down.
Comparator Example: A practical example is an electrical comparator with different thresholds for increasing and decreasing signals. No matter how fast or slow the input signal changes, the output only changes when these specific thresholds are crossed¹.
Imagine you’re painting a picture. You add colors one by one, layer by layer. Whether you paint quickly or take your time, the sequence of colors and the final picture remain the same. The painting process shows rate-independent hysteresis because the final outcome doesn’t depend on the speed of your brushstrokes.
Rate-independent hysteresis is like a story that unfolds the same way, no matter how quickly or slowly you read it. The system’s history determines its current state, not the rate at which the changes occur.
Hysteresis Loop
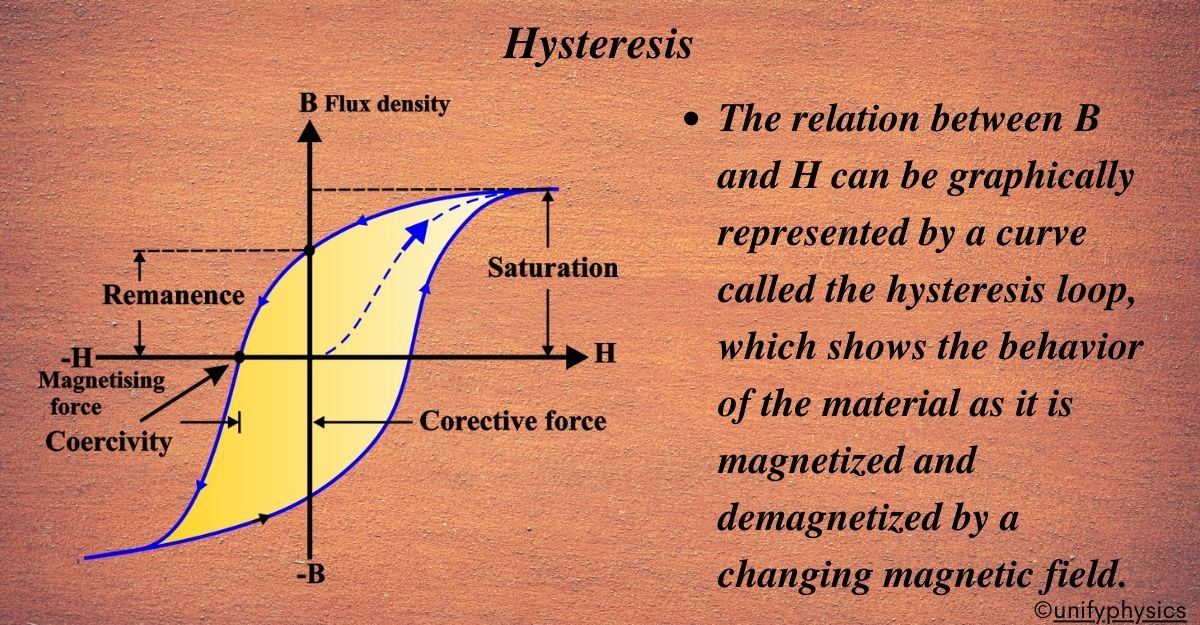
A Hysteresis Loop is a graphical representation of the relationship between B and H. As the magnetic field is cycled, the path of B forms a loop, which is key to understanding a material’s magnetic properties.
The relation between B and H in ferromagnetic materials is nonlinear and depends on the history of the material. B is the magnetic flux density, which measures the strength and direction of the magnetic field. H is the magnetic field intensity, which measures the external magnetic field that induces magnetization in the material.
The magnetization of a ferromagnetic material is the net magnetic moment per unit volume, which is caused by the alignment of the magnetic domains in the material. The magnetic domains are small regions where the atomic magnetic moments are aligned in parallel. The relation between B and H can be expressed by the equation:
\(\displaystyle B = \mu_0 (H + M)\)
- µ0 is the permeability of free space, which is a constant value of \(\displaystyle 4\pi \times 10^{-7}\) H/m.
- M is the magnetization of the material, which depends on the magnetic history of the material.
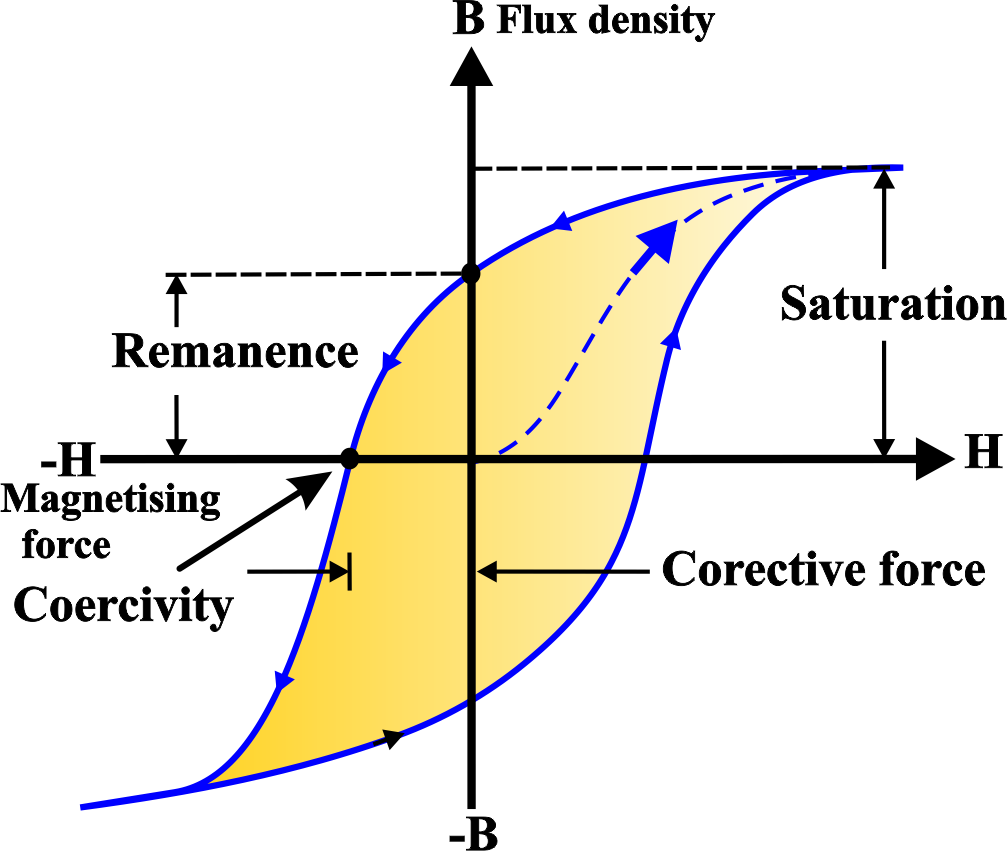
The relation between B and H can be graphically represented by a curve called the hysteresis loop, which shows the behavior of the material as it is magnetized and demagnetized by a changing magnetic field.
The hysteresis loop has the following features:
- The initial magnetization curve shows how the material is magnetized from zero to saturation, where all the domains are aligned with the external field.
- The saturation point is the maximum value of B that the material can attain for a given value of H.
- The remanence or residual magnetism is the value of B that remains when H is reduced to zero, which indicates the permanent magnetism of the material.
- The coercivity or coercive force is the value of H that is required to reduce B to zero, which indicates the resistance of the material to demagnetization.
- The hysteresis loss is the area enclosed by the loop, which represents the energy dissipated as heat due to the repeated magnetization and demagnetization of the material.
How does temperature affect the shape of a hysteresis loop?
Temperature has a significant impact on the shape of a hysteresis loop. Here’s how it works:
At Lower Temperatures: When the temperature is low, the hysteresis loop tends to be wider. The magnetic domains are more aligned and can maintain their state with less thermal agitation. The material’s magnetization changes more significantly with the applied magnetic field, resulting in a broader loop.
Increasing Temperature: As the temperature rises, the thermal energy increases, which causes more random movement of the magnetic domains. This random movement can disrupt the alignment of the domains, making it harder for the material to reach full saturation. The loop becomes narrower and less pronounced.
Near the Curie Point: The Curie point is the temperature at which a ferromagnetic material loses its permanent magnetic properties and becomes paramagnetic. As the temperature approaches the Curie point, the hysteresis loop shrinks further and eventually disappears because the thermal agitation overcomes the magnetic forces keeping the domains aligned.
“As temperature increases, the hysteresis loop area decreases due to reduced magnetisation, following Curie’s Law: χ ∝ 1/T”
\(\displaystyle B=\mu_0(H + M)\)
Magnetisation and Susceptibility:
\(\displaystyle M=\chi H\)
Where χ is magnetic susceptibility, the measure of how much the material gets magnetised in response to H.
Substitute into the first equation: \(\displaystyle B=\mu_0(H + M)\)
\(\displaystyle B= \mu_0(H + \chi H) = \mu_0 H(1 + \chi)\)
Now, Introduce Temperature Using Curie’s Law: χ=CT
(Curie’s Law for paramagnetic and ferromagnetic materials above Curie temperature). Thus,
\(\displaystyle B= \mu_0 H \left(1 + \frac{C}{T}\right)\)
As temperature T increases, susceptibility χ decreases. That means magnetisation M becomes weaker for the same applied field H. Hence, B becomes smaller than before for the same H, leading to a narrower hysteresis loop.
Phase Transitions: Some materials undergo phase transitions at certain temperatures, which can cause abrupt changes in the hysteresis loop. For example, a material might exhibit a sudden increase in polarization due to a phase transition, altering the shape of the loop.
Energy Loss: The area within the hysteresis loop represents the energy lost as heat during a cycle of magnetization and demagnetization. As temperature increases, the loop can widen, indicating greater energy loss in the material, which is particularly important in the design of transformers and other magnetic devices where minimizing energy losses is crucial.
So, the temperature affects the hysteresis loop by influencing the alignment and movement of magnetic domains within a material. The loop’s shape can tell us much about the material’s magnetic properties and how they change with temperature.
Advantages of Hysteresis Loop
- Understanding Material Properties: The hysteresis loop helps us understand important properties of magnetic materials, such as how they become magnetized and demagnetized. It’s like a map that shows us the magnetic journey of a material.
- Measuring Retentivity and Coercivity: The loop gives us a visual representation of retentivity (the material’s ability to retain magnetism) and coercivity (the resistance to becoming demagnetized). It’s like knowing how sticky material is to magnetism and how much effort it takes to scrub that magnetism off.
- Energy Loss Insight: The area inside the loop indicates the energy lost as heat during magnetization and demagnetization cycles. A smaller loop area means less energy loss, which is crucial when designing efficient electrical devices.
- Selecting Materials: By looking at the loop, engineers can choose the right material for making permanent magnets or for use in machines like transformers and motors. It’s like picking the right player for your team based on their stats.
- Predicting Behavior: The shape and size of the loop can predict how a material will behave under different magnetic conditions. This is important for applications where magnetic properties are critical, such as in data storage or electronic components.
- Residual Magnetism: From the loop, we can calculate residual magnetism, which helps in selecting materials for electromagnets. It’s like knowing how much charge a battery can hold after it’s been used.
In essence, the hysteresis loop is a powerful tool that provides information about magnetic materials. It’s like a character profile that tells us everything we need to know about how a material will perform in magnetic roles.
Magnetization and Demagnetization
Magnetization
Magnetization is the process of aligning a material’s magnetic domains to create a magnet. Imagine you have a collection of tiny compasses, each with its little needle that can point in any direction. Now, these compasses represent the magnetic domains in a material—small regions where the magnetic moments of atoms are aligned in the same direction.
Initially, these compass needles (domains) are all pointing in random directions, just like in an unmagnetized piece of iron. There’s no strong overall magnetic field because the tiny magnetic fields of each domain cancel each other out.
Now, let’s say you bring a strong magnet close to this material. This is like a strong wind blowing over your compasses, pushing all the needles to point in the same direction. As the external magnetic field influences the domains, they start to align with the field.
As more and more domains align, the material itself starts to act like a magnet. This process is called magnetization. It’s the degree to which the material gets magnetized when exposed to an external magnetic field.
If the external magnetic field is strong enough, eventually, all the domains will align, and the material reaches a state called saturation. At this point, the material is fully magnetized, and its internal magnetic field is as strong as it can get.
What happens if you take the strong magnet away? Some of the compass needles might stay aligned, giving the material residual magnetism. This is why some materials can become permanent magnets.
The strength of magnetization can be measured and is denoted by M. It’s defined as the magnetic moment per unit volume of the material. In a formula, it looks like this:
\(\displaystyle M = \frac{\text{Total Magnetic Moment}}{\text{Volume}} \)
Magnetization is about turning a disorganized crowd of magnetic domains into an orderly march, all pointing in the same direction, transforming the material into a magnet.
Various Methods To Achieve Magnetization:
- Rubbing with a Magnet: This is like combing your hair in one direction. When you rub a piece of iron with a magnet, always in the same direction, the magnetic domains start to align with the magnet’s field, just like your hair aligns with the comb’s path.
- Using an Electromagnet: Imagine using a giant magnet to organize a crowd to move in one direction. An electromagnet can be used to magnetize a material by placing the material within its magnetic field. The electric current through the electromagnet creates a strong magnetic field that aligns the domains.
- Hammering: It’s like tapping a group of dancers to sync their steps. Hammering a material in the presence of a magnetic field can cause the domains to align with the field’s direction. Each tap nudges the domains a bit closer to alignment.
- Heating and Cooling: Think of it as a reset button. Heating a material to a high temperature and then cooling it in the presence of a magnetic field can align the domains. The heat shakes up the domains, and as they cool down, they settle in the direction of the magnetic field.
- Static Magnetization: This method involves exposing the material to a constant magnetic field. It’s like pressing ‘play’ on a song and letting it run. The continuous presence of the magnetic field gradually aligns the domains.
- Pulse Magnetization: This is like a series of claps that guide the crowd to move rhythmically. Short, intense bursts of magnetic field are used to quickly align the domains. It’s effective for strong magnets or when a specific magnetization pattern is needed.
Each of these methods has its advantages and is suitable for different types of materials and applications.
Demagnetization
Demagnetization is reducing or eliminating a material’s magnetization. Imagine a school where all the students are standing in neat rows during assembly. This is like a magnetized material, where all the magnetic domains are aligned, creating a strong magnetic field. Now, what if the school bell rings and the students start to disperse in different directions? The order is lost, and so is the neat formation. This is similar to demagnetization.
When a material is demagnetized, the orderly arrangement of its magnetic domains (like the students in rows) becomes disordered. The domains start pointing in random directions, canceling out each other’s magnetic fields.
Causes of Demagnetization: Several factors can cause demagnetization:
- Heat: Just like heat can make people feel lethargic and less organized, heating a magnet can cause the domains to move randomly, leading to demagnetization.
- Hammering: Hammering a magnet is like shaking the ground beneath the students’ feet. It disrupts the alignment of the domains, causing demagnetization.
- Electrical Methods: Passing an alternating current through a magnet is like changing the school bell’s sound repeatedly. The changing magnetic field confuses the domains, leading to their random orientation.
Once demagnetized, the material no longer behaves like a magnet. It won’t attract iron filings or stick to the fridge. It’s like the school assembly dispersing, and the order is gone.
Sometimes, demagnetization can be reversed by re-magnetizing the material, just like the students can be called back to form neat rows again. However, some materials might not regain their full magnetic strength.
Demagnetization is important in many applications. For instance, demagnetizing tools can prevent them from picking up unwanted metal filings, and demagnetizing tapes can erase data stored magnetically.
So, demagnetization is about losing the magnetic order that was once established. It’s a return to randomness from a state of alignment, and it plays a crucial role in understanding how magnets work and how they can be used or reused.
Various Methods To Achieve Demagnetization:
- Heating: Imagine you’re at a party where everyone is dancing in sync. Now, turn up the heat! As it gets hotter, people start to move more randomly and the synchronized dance is lost. Similarly, heating a magnet (especially beyond its Curie point) makes the orderly magnetic domains move randomly, leading to demagnetization.
- Hammering: Think of a well-organized library with books neatly arranged. If you start shaking the shelves (hammering), books (magnetic domains) will fall out of order. Hammering a magnet disrupts the alignment of its domains, causing it to lose its magnetism.
- Electrical Method: Using an alternating current is like changing the music’s rhythm rapidly at a party. The dancers (domains) can’t keep up and end up moving chaotically. Passing an alternating current through a magnet causes the domains to change direction rapidly, leading to demagnetization.
- Adiabatic Demagnetization: This method is like cooling down the dancers with a powerful air conditioner after they’ve been heated up by dancing. In adiabatic demagnetization, a material is cooled to such an extent that the thermal motion of the domains decreases significantly, reducing their magnetic alignment.
- Mishandling or Poor Storage: Just like a deck of cards will get shuffled if not handled carefully, magnets can lose their magnetism if they’re dropped or stored improperly. The physical jostling can misalign the domains, leading to a loss of magnetism over time.
These methods show how demagnetization can be achieved by disrupting the order and alignment of magnetic domains within a material. It’s a process of taking a material from a state of magnetic coherence to one of randomness.
Energy Loss due to Hysteresis
When a magnetic material is cycled through a hysteresis loop, energy is lost as heat. This is known as hysteresis loss. Imagine you’re at a water park on a circular lazy river ride. You have to push yourself to start moving, but once you’re going, you keep going around in a loop. Now, imagine that each time you complete a loop, some of the water splashes out of the river. This loss of water is similar to the energy loss in hysteresis.
As we’ve discussed, the hysteresis loop is a graphical representation of the magnetic properties of a material. It shows how the magnetic flux density (B) changes with the magnetic field strength (H).
Just like you need to push yourself to keep moving in the lazy river, energy is needed to change the magnetization of a material. When you magnetize and demagnetize a material, you’re essentially pushing it through the hysteresis loop.
Not all the energy you put into the system comes back out. Some of it is lost as heat due to the internal friction-like resistance within the material. This is the energy loss due to hysteresis.
The area inside the hysteresis loop represents the amount of energy lost per cycle of magnetization and demagnetization. A larger loop area means more energy loss, just like more water splashing out means a wetter ride.
In devices like transformers and motors, this energy loss appears as heat, which can affect efficiency and performance. Engineers need to consider this when designing such devices to minimize energy loss.
So, energy loss due to hysteresis is like the water splashed out in each loop of the lazy river—it’s the price you pay for the ride. It’s an important concept because it helps us understand and manage the efficiency of magnetic devices.
Retentivity and Coercivity
Retentivity is the ability of a material to retain magnetization after the external field is removed.
Retentivity (Remanence):
Retentivity is the ability of a material to retain or resist magnetization after the removal of the external magnetic field. It depends on the hysteresis curve of the material, which is a plot of the magnetic flux density (B) versus the magnetic field intensity (H) for a complete cycle of magnetization and demagnetization.
The retentivity is the value of the magnetic flux density when the magnetic field intensity is zero after the material has been magnetized to saturation. It is also called the residual magnetism or the remanence. The retentivity is high for ferromagnetic materials, meaning they can retain a large amount of magnetization even without an external field.
Imagine you have a group of dancers who have learned a dance routine by heart. Even after the music stops, they can continue dancing because they remember the moves. This memory of the dance routine is similar to the concept of retentivity in magnetic materials.
Just like the dancers remember the routine, magnetic materials have a “memory” of their magnetized state. This memory is due to the alignment of tiny regions called magnetic domains.
When the external magnetic field is taken away, like when the music stops, a material with high retentivity will keep a significant level of magnetization, just as the dancers continue their routine even without the music.
Materials with high retentivity make good permanent magnets because they can maintain a strong magnetic field on their own, much like how skilled dancers can perform flawlessly even without cues.
On a hysteresis loop, retentivity is represented by the level of magnetization that remains after the external magnetic field has been reduced to zero. It’s like marking the spot where the dancers continue to move even after the music has stopped. For diamagnetic and paramagnetic materials, the retentivity is zero, meaning they lose all their magnetization when the external field is removed.
Coercivity:
Coercivity is the ability of a material to withstand the external magnetic field without becoming demagnetized. It is the minimum value of the magnetic field intensity required to reduce the magnetization of the material to zero after the material has been magnetized to saturation. It is also called the coercive force or the coercive field.
Imagine you’re trying to push a heavy box across the floor. Initially, it’s tough to get the box moving, but once it starts sliding, it becomes easier. Now, if you want to stop the box and push it back to where it started, you need to exert a lot of force again. This resistance to change in motion is similar to coercivity in magnetic materials.
Just like the box resists being pushed, magnetic materials resist being demagnetized. Coercivity is the strength of the magnetic field required to bring the magnetization of a material down to zero after it has been fully magnetized.
When you try to demagnetize a material (push the box back), you need to apply a magnetic field in the opposite direction. The coercivity is how strong this field needs to be to overcome the material’s “desire” to stay magnetized.
Materials with high coercivity make good permanent magnets because they don’t easily lose their magnetization. They’re like a box that’s very hard to push back, so it stays put where you pushed it to.
On a hysteresis loop, coercivity is represented by the magnetic field strength at which the magnetization curve crosses the horizontal axis on its way back to zero. It’s like marking the point where you’ve pushed the box back to its starting position. In essence, coercivity is about how much a magnetic material “wants” to remain magnetized and how much effort (magnetic field strength) it takes to change that.
The coercivity is high for ferromagnetic materials, meaning they require a large amount of external field to be demagnetized. For diamagnetic and paramagnetic materials, the coercivity is zero, meaning they can be easily demagnetized by a small external field.
Also Read: Magnetic Properties of Materials
Difference between Soft Magnets and Hard Magnets
This table summarizes the key differences between soft and hard magnetic materials based on their magnetic properties and applications. Soft magnets are typically used in applications where ease of magnetization and demagnetization are important, like in electrical machines. Hard magnets, on the other hand, are used where a permanent magnetic field is needed, such as in speakers or hard drives.
| Property | Soft Magnets | Hard Magnets |
|---|---|---|
| Definition | Easily magnetized and demagnetized materials. | Materials that maintain their magnetism after being magnetized. |
| Permeability | High (allows magnetic field lines to pass through easily). | Low (resists the passage of magnetic field lines). |
| Coercivity | Low (requires a small magnetic field to demagnetize). | High (requires a large magnetic field to demagnetize). |
| Retentivity | Low (loses magnetization quickly when the field is removed). | High (retains significant magnetization after the field is removed). |
| Hysteresis Loop | Narrow (indicating less energy loss during magnetization cycles). | Wide (indicating more energy loss during magnetization cycles). |
| Energy Stored | Less (due to low retentivity). | More (can store higher energy in the magnetic field). |
| Applications | Transformers, inductors, electromagnetic cores. | Permanent magnets, magnetic sensors, data storage. |
| Examples | Silicon steel, soft ferrites, iron-nickel alloys. | Alnico, neodymium-iron-boron (NdFeB) magnets. |
Hysteresis Applications
Hysteresis is not just a concept stuck in physics textbooks; it’s a phenomenon that has practical uses in our daily lives. Here are some of the key applications:
- Memory Storage: Just like your brain remembers information, hysteresis helps in memory storage in devices like hard disks and magnetic tapes. The hysteresis loop allows these devices to retain data by maintaining magnetic states.
- Electrical Engineering: In electrical circuits, hysteresis is used to prevent unwanted rapid switching. For example, in a thermostat, hysteresis ensures that the heating system doesn’t turn on and off too quickly, which could wear out the system and be inefficient.
- Control Systems: Hysteresis is used in designing control systems for machines and processes that require precise regulation of variables like temperature, pressure, and flow rate. It helps in maintaining stability and reliability in these systems.
- Motors: Hysteresis motors, which are known for their smooth operation, rely on the hysteresis effect for their functioning. They are used in equipment where precise speed control is essential, like in record players and electric clocks.
- Sensors and Switches: Magnetic switches and relays use hysteresis to maintain a state until a certain threshold is reached. This makes them reliable and predictable, which is crucial for safety and performance.
- Sound Equipment: In sound recording and producing equipment, hysteresis ensures that the devices respond accurately to the magnetic fields used to record and reproduce sound, resulting in high-quality audio.
Solved Examples
Problem 1: A ferromagnetic material has a hysteresis loop such that the magnetic field required to reduce the magnetization to zero from saturation is (200 A/m). Calculate the coercivity of the material.
Solution: Coercivity (Hc) is the magnetic field required to bring the magnetization to zero from saturation.
Given: The magnetic field to reduce magnetization to zero (Hc = 200 A/m)
The coercivity of the material is ( 200 A/m).
Problem 2: A ferromagnetic material has a hysteresis loop with a retentivity of (0.5 T). If the maximum magnetization is (1.2T), calculate the percentage of retentivity with respect to the maximum magnetization.
Solution: Retentivity (Br) is the residual magnetic flux density when the magnetic field is zero.
Given: Retentivity (Br = 0.5 T); Maximum magnetization (Bmax = 1.2 T)
Percentage of retentivity:
\(\displaystyle \text{Percentage of Retentivity} = \left( \frac{B_r}{B_{\text{max}}} \right) \times 100 \% \)
\(\displaystyle \text{Percentage of Retentivity} = \left( \frac{0.5}{1.2} \right) \times 100 \% \)
\(\displaystyle \text{Percentage of Retentivity} \approx 41.67 \% \)
The percentage of retentivity with respect to the maximum magnetization is approximately (41.67 % ).
Problem 3: A magnetic material with a volume of (0.1 m3) undergoes a hysteresis cycle, losing ( 500 J) of energy per cycle. Calculate the hysteresis loss per unit volume.
Solution: Hysteresis loss per unit volume is given by the total energy loss divided by the volume.
Given: Energy loss per cycle (E = 500 J); Volume (V = 0.1 m3)
Hysteresis loss per unit volume:
\(\displaystyle \text{Hysteresis Loss per Unit Volume} = \frac{E}{V} \)
\(\displaystyle\text{Hysteresis Loss per Unit Volume} = \frac{500}{0.1}\)
\(\displaystyle\text{Hysteresis Loss per Unit Volume} = 5000 \, \text{J/m}^3\)
The hysteresis loss per unit volume is (5000 J/m3).
Problem 4: A ferromagnetic material with a coercivity of (300 A/m) and retentivity of (0.6 T) is subjected to an external magnetic field of (200 A/m). Calculate the magnetic flux density (B) in the material, assuming a linear approximation between retentivity and coercivity.
Solution: Using a linear approximation between retentivity (Br) and coercivity (Hc):
\(\displaystyle B = B_r \left(1 – \frac{H}{H_c}\right) \)
Given: Br = 0.6 T; Hc = 300 A/m; H = 200 A/m.
Calculate (B):
\(\displaystyle B = 0.6 \left(1 – \frac{200}{300}\right) \)
\(\displaystyle B = 0.6 \left(1 – \frac{2}{3}\right) \)
\(\displaystyle B = 0.6 \left(\frac{1}{3}\right) \)
\(\displaystyle B = 0.2 \, \text{T} \)
The magnetic flux density (B) in the material is (0.2T).
Problem 5: A ferromagnetic material requires a magnetic field of (500 A/m) to be magnetized to saturation. If the material is subjected to a maximum field of (800 A/m), determine the ratio of the maximum field to the saturation field.
Solution: Saturation magnetic field (Hsat= 500 A/m); Maximum magnetic field ( Hmax = 800 A/m).
The ratio of the maximum field to the saturation field:
\(\displaystyle \text{Ratio} = \frac{H_{\text{max}}}{H_{\text{sat}}} \)
\(\displaystyle \text{Ratio} = \frac{800}{500} \)
\(\displaystyle \text{Ratio} = 1.6 \)
The ratio of the maximum field to the saturation field is (1.6).
Problem 6: The area of the hysteresis loop for a certain magnetic material is (\(\displaystyle 4 \times 10^{-3} \, \text{J} \)). If the volume of the material is (0.2 m3) and the frequency of the applied magnetic field is (50 Hz), calculate the power loss due to hysteresis.
Solution: The power loss due to hysteresis is given by:
\(\displaystyle P = \text{Area of Hysteresis Loop} \times \text{Volume} \times \text{Frequency} \)
Given: Area of hysteresis loop (\(\displaystyle A = 4 \times 10^{-3} \, \text{J}\)); Volume (V = 0.2 m3); Frequency (f = 50 Hz)
Calculate (P):
\(\displaystyle P = (4 \times 10^{-3}) \times 0.2 \times 50 \)
\(\displaystyle P = 4 \times 10^{-3} \times 10 \)
\(\displaystyle P = 4 \times 10^{-2} \, \text{W} \)
P = 0.04 W
The power loss due to hysteresis is (0.04 W).
FAQs
What is hysteresis in the context of magnetic materials?
Hysteresis refers to the lag between changes in magnetization of a material and the changes in the applied magnetic field. It is depicted as a loop in the plot of magnetic field strength (H) versus magnetic flux density (B), indicating that the path of magnetization differs from the path of demagnetization.
Why is the hysteresis loop important in understanding magnetic materials?
The hysteresis loop provides valuable information about the magnetic properties of a material, including its coercivity, retentivity, and energy loss. These parameters are crucial for determining the material’s suitability for various applications, such as transformers, magnetic storage, and permanent magnets.
What is coercivity in the context of hysteresis?
Coercivity is the measure of the strength of the external magnetic field that must be applied to a magnetized material to reduce its magnetization to zero. It is a key property derived from the hysteresis loop and indicates the resistance of a material to becoming demagnetized.
What does retentivity mean in a hysteresis loop?
Retentivity, also known as remanence, is the measure of the residual magnetic flux density that remains in a material after the external magnetic field is removed. It indicates the material’s ability to retain magnetization and is an important characteristic of permanent magnets.
How does hysteresis relate to energy loss in magnetic materials?
Energy loss in magnetic materials due to hysteresis is known as hysteresis loss. It occurs because of the lag between the applied magnetic field and the resulting magnetization, causing heat to be generated within the material. This loss is proportional to the area of the hysteresis loop.
What is the significance of the shape and area of the hysteresis loop?
The shape and area of the hysteresis loop provide insights into the material’s magnetic properties. A narrow loop indicates low hysteresis loss and is typical for soft magnetic materials, while a wide loop indicates high hysteresis loss, characteristic of hard magnetic materials. The area of the loop directly relates to the energy dissipated as heat during each cycle of magnetization and demagnetization.
Can hysteresis be observed in materials other than magnetic ones?
Yes, hysteresis is a phenomenon that can occur in various physical systems, not just magnetic materials. It can be observed in systems involving elasticity, electrical systems with ferroelectric materials, and even in economic and biological systems where there is a dependence on historical states or inputs.