The story of Coulomb’s Law begins with a French physicist named Charles-Augustin de Coulomb. In 1785, Coulomb made a groundbreaking discovery that would become a cornerstone of electrostatics. He was interested in understanding the forces that charged objects exert on each other.
Coulomb conducted a series of experiments using a torsion balance, which is a delicate instrument capable of measuring very small forces. With this device, he was able to observe the behavior of electrically charged objects and how they interacted with each other at various distances.
Through his experiments, Coulomb found that there was a clear mathematical relationship between the force exerted by the charges and the distance separating them. He discovered that the force was directly proportional to the product of the charges and inversely proportional to the square of the distance between them. This relationship is what we now call Coulomb’s Law.
Coulomb’s findings were significant because they provided a quantitative description of the electrostatic force, allowing for precise calculations. His work laid the foundation for the development of the theory of electromagnetism and has been instrumental in advancing our understanding of electric forces.
Coulomb’s Law was one of the first to describe the force between charges with a mathematical equation, and it remains a fundamental principle in physics to this day. It’s a perfect example of how careful observation and experimentation can lead to a deeper understanding of the natural world.
By studying Coulomb’s work, students can appreciate the importance of empirical evidence in the formulation of scientific laws and the impact that such discoveries can have on technology and our understanding of the universe.
Coulomb’s Law describes the electrostatic force between two charged particles. The law was formulated by French physicist Charles-Augustin de Coulomb in the 18th century. It quantifies the force between two-point charges and is fundamental to understanding the behavior of charged particles.
What is Coulomb’s Law?
Definition:
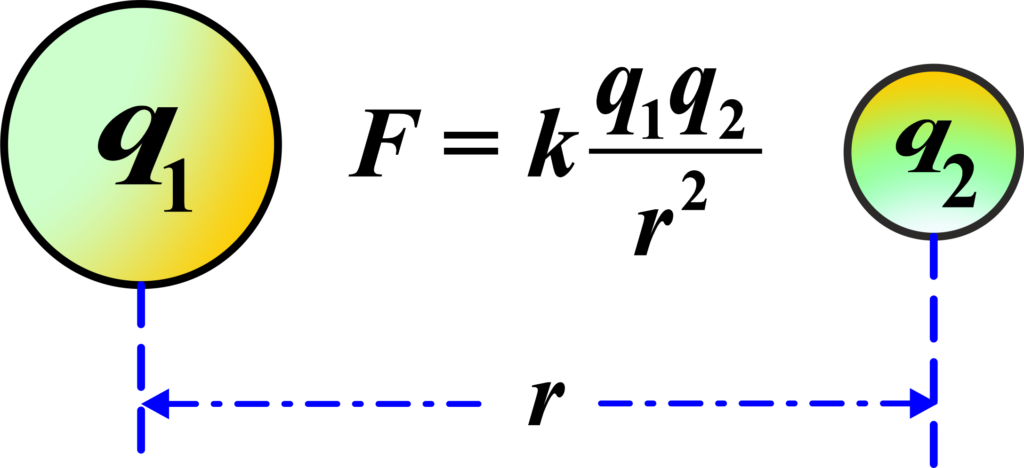
”The force (F) between two charges (q1 and q2) is directly proportional to the product of the magnitudes of the charges and inversely proportional to the square of the distance (r) between them.”
Coulomb’s Law (Scalar Form)
Imagine you have two magnets. When you bring them close, they either pull towards each other or push away, depending on which ends you put together. Now, replace those magnets with objects that have electric charges, and you have the essence of Coulomb’s Law.
\(\displaystyle F \propto q_{1} q_{2} \hspace{1cm}\) and \(\displaystyle \hspace{1cm} F \propto \frac{1}{r^2}\)
Coulomb’s Law is a scientific rule that tells us how strong the force will be between two electrically charged objects. It’s like a recipe for understanding electric forces. Here’s the formula:
\(\displaystyle\begin{equation}\label{eqn:1}\boxed{\boldsymbol{F = k \frac{|q_1 \cdot q_2|}{r^2} }} \end{equation}\)
- (F) stands for the force between the charges. It’s like the pull or push you feel between the magnets.
- (q1) and (q2) are the amounts of charge on the two objects. Charges can be positive or negative, just like the two different ends of a magnet.
- (r) is the distance between the charges. The further apart they are, the weaker the force.
- (k) is a number called Coulomb’s constant (about 8.99 × 109 N·m²/C²), which helps us use the right units and makes the formula work in the real world.
In simple terms, Coulomb’s Law says that:
- If you increase the charges, the force gets stronger.
- If you increase the distance, the force gets weaker.
- The force can be attractive (pulling together) if the charges are opposite, or repulsive (pushing apart) if the charges are the same.
And that’s Coulomb’s Law! It’s a fundamental part of physics that helps us predict how charged objects will behave, much like how we can predict the behavior of magnets. Remember, this law only works when the charges are still and not moving around.
Coulomb’s Law in Vector Form
When we talk about vectors in physics, we’re not just interested in how strong something is, but also in which direction it’s going. The vector form of Coulomb’s Law tells us not only the strength of the force between two charges but also the direction in which this force acts.
The force is attractive if the charges are of opposite signs and repulsive if they are of the same sign. We can write coulomb law as
\(\displaystyle \vec{F}_{12} = k \frac{q_1 \cdot q_2}{r^2} \hat{r}_{12} \)
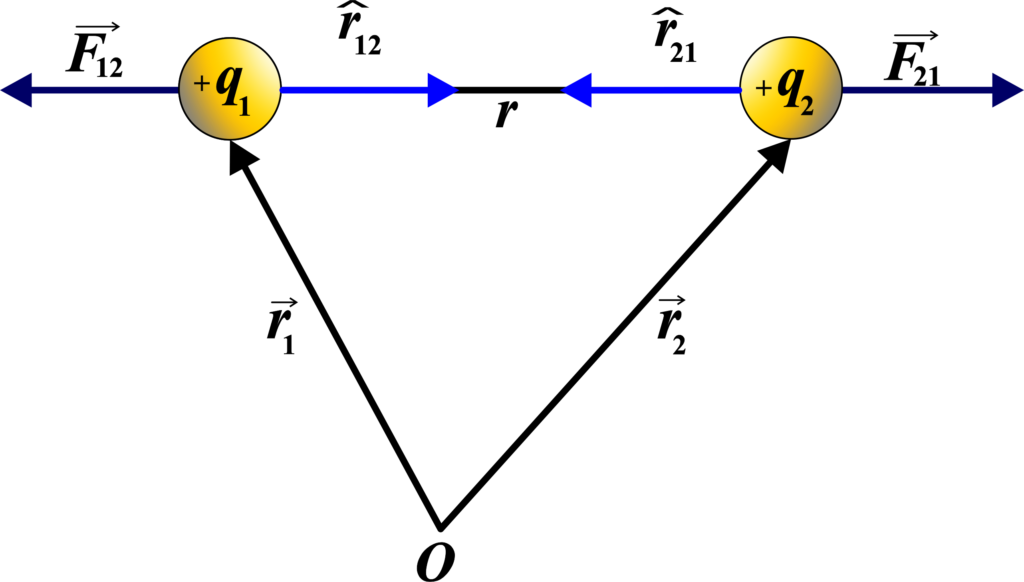
Let us consider, that two-point charges +q1 and +q2 are separated at a distance r in a vacuum as shown in the figure.
To derive the vector form, we’ll start with the scalar form and then add the direction using vectors. We know the scalar form of Coulomb’s Law is:
\(\displaystyle F = k \frac{|q_1 \cdot q_2|}{r^2} \)
To convert this into a vector form, we need to consider the direction of the force. We do this by introducing a unit vector \(\displaystyle \hat{r} \).
The unit vector \(\displaystyle \hat{r}_{12} \) points from charge (q1) to charge (q2) and is defined as:
\(\displaystyle \hat{r}_{12} = \frac{\vec{r}_{12}}{|\vec{r}_{12}|} \)
where \(\displaystyle \vec{r}_{12} \) is the position vector pointing from (q1) to (q2), and \(\displaystyle |\vec{r}_{12}| \) is its magnitude (or length).
Now, we multiply the scalar form of the force by the unit vector to give it a direction:
\(\displaystyle \vec{F}_{12} = F \cdot \hat{r}_{12} \)
Replace (F) with the scalar form of Coulomb’s Law:
\(\displaystyle \vec{F}_{12} = k \frac{|q_1 \cdot q_2|}{r^2} \cdot \hat{r}_{12} \)
Since we’re now dealing with vectors, we don’t need the absolute value. The direction of the force will be taken care of by the unit vector. So, we have:
\(\displaystyle \vec{F}_{12} = k \frac{q_1 \cdot q_2}{r^2} \cdot \hat{r}_{12} \)
This is the vector form of Coulomb’s Law, which tells us the magnitude and direction of the electrostatic force between two point charges.
So, the final expression for the vector form of Coulomb’s Law is:
\(\displaystyle\begin{equation}\label{eqn:2}\boxed{\boldsymbol{\vec{F}_{12} = k \frac{q_1 \cdot q_2}{r^2} \hat{r}_{12} }} \end{equation}\)
This formula says that the electrostatic force \(\displaystyle \vec{F}_{12} \) between two charges (q1) and (q2) is directly proportional to the product of the charges, inversely proportional to the square of the distance between them, and acts along the line connecting the charges.
Also Read: Electric Charge
1 Coulomb Of Charge?
One Coulomb is the amount of charge transferred by a current of one ampere flowing for one second. It’s a large unit; even a small spark of static electricity is much less than a Coulomb.
Think of electric charge as if it were a bucket of water. Now, 1 Coulomb (C) is like a specific measure of that water. But instead of measuring water, we’re measuring something called electric charge.
Here’s a fun fact: 1 Coulomb is a pretty big amount of charge. If you had a balloon with a charge of 1 Coulomb, it would have a huge force pushing against another balloon with the same charge, even from a distance!
To put it in perspective, 1 Coulomb is the amount of charge that passes through a light bulb when a current of 1 ampere flows for 1 second. It’s like saying, “If we let the water flow from a tap at a rate of 1 liter per second, after one second, we’ll have 1 liter of water.” Similarly, if we let electric charge flow at a rate of 1 ampere (which is just a fancy way of saying “1 Coulomb per second”), after one second, we’ll have 1 Coulomb of charge.
In technical terms:
\(\displaystyle 1 \text{ Coulomb} = 1 \text{ Ampere} \times 1 \text{ Second} \)
So, when you’re dealing with charges in physics, just remember that 1 Coulomb is a standard measure, like a liter for liquid or a meter for distance, but for the amount of electricity.
Variation of Relative Permittivity
Imagine you’re trying to talk to your friend who’s a little way down the beach. If it’s just air between you two, they can hear you pretty well. But what if there’s a party with loud music between you? The music is like a material that changes how well your voice carries over to your friend.
Relative permittivity is a bit like that. It tells us how a material changes the “conversation” between two charges compared to when there’s just space (or a vacuum) between them.
Here’s how it ties in with Coulomb’s Law:
- Coulomb’s Law says the force between two charges is:
\(\displaystyle F = k \frac{q_1 \cdot q_2}{r^2} \) - But when you put a material between the charges, the force changes. The new force is:
\(\displaystyle F’ = \frac{F}{\varepsilon_r} \)
where (F’) is the force with the material present, and \(\displaystyle \varepsilon_r \) is the relative permittivity of the material.
So, relative permittivity \(\displaystyle\varepsilon_r \) is the factor by which the material reduces the force between the charges. It’s a number without units, and it varies from material to material:
- In a vacuum, \(\displaystyle\varepsilon_r \) is 1 (no change to the force).
- In the air, it’s just a little more than 1.
- In water, it’s about 80, which means water reduces the force a lot.
This variation is crucial because it affects how electric fields behave inside different materials. For example, in capacitors, we use materials with high relative permittivity to increase their ability to store charge.
In summary, the variation of relative permittivity shows us how different materials can “soften” or “dampen” the electric conversation between charges, which is a key concept in designing electronic devices and understanding electric interactions in different environments.
Limitation of Coulomb’s Law
- Only for Static Charges: Coulomb’s Law works for charges that are chilling out and not moving. If they start to move, the law doesn’t apply because moving charges create magnetic fields too.
- Point Charges Assumption: The law assumes charges are like tiny dots with no size. But in real life, charges have some volume, and this can affect the force between them.
- No Medium Effects: Coulomb’s Law is based on the idea that charges are in a vacuum. But we live in the real world, where air, water, and other materials can change how charges interact.
- Non-Relativistic: The law doesn’t consider Einstein’s theory of relativity. So, if charges start zooming close to the speed of light, Coulomb’s Law won’t give the right answers.
- Coulomb’s Law is all about electric forces. It doesn’t take into account other forces like gravity or magnetic forces that can also affect charged particles.
Applications of Coulomb’s Law
Coulomb’s Law is like the rules of a game that tells us how charged particles interact. Just like knowing the rules of soccer helps you understand how players move and score, Coulomb’s Law helps us predict how charges will behave. Here are some ways this law is applied in the real world:
- Electrostatics Experiments: In physics labs, Coulomb’s Law is used to calculate the forces between charged objects, helping students see the law in action.
- Designing Capacitors: Engineers use Coulomb’s Law to design capacitors, which are devices that store electric charge in circuits.
- Understanding Atoms: The law explains the forces that hold electrons in orbit around the nucleus, which is essential for chemistry and materials science.
- Electric Field Mapping: Coulomb’s Law helps us draw electric field lines around charges, which is crucial for visualizing and understanding electric fields.
- Electrostatic Precipitators: These are devices that clean industrial smoke by using electric forces to remove dust particles, all based on Coulomb’s Law.
- Inkjet Printers: They use electric charges to direct tiny droplets of ink onto paper with precision.
- Touchscreens: Devices like smartphones and tablets use changes in the electric field, calculated through Coulomb’s Law, to detect touch.
- Particle Physics: Coulomb’s Law is foundational in particle accelerators, which are machines that speed up charged particles for research.
- Medical Treatments: Techniques like electrotherapy, which uses electric charges to promote healing, rely on principles from Coulomb’s Law.
- Electrostatic Force Microscopy: This technology uses the forces described by Coulomb’s Law to image surfaces at the atomic level.
Solved Examples
Example 1: Two point charges, (q1 = 3 µC ) and ( q2 = -5 µC ), are placed 2 meters apart in the air. Calculate the magnitude and direction of the electric force between them.
Solution: Given: ( q1 = 3 µC ), ( q2 = -5 µC ), ( r = 2m ), ( k = = 9 × 109 N.m2/C2)
Magnitude of electric force:
\(\displaystyle F = \frac{k |q_1 q_2|}{r^2} \)
\(\displaystyle F = \frac{9 \times 10^9 \times |3 \times 10^{-6} \times -5 \times 10^{-6}|}{(2)^2} \)
\(\displaystyle F = \frac{9 \times 10^9 \times 15 \times 10^{-12}}{4} \)
\(\displaystyle F = \frac{135 \times 10^{-3}}{4} \)
\(\displaystyle F = 33.75 \times 10^{-3} \)
\(\displaystyle F = 3.375 \times 10^{-2} \, N \)
The direction of the force is attractive since the charges are of opposite sign.
Example 2: Two charges of (2 µC) and (-3 µC) respectively are placed 10 cm apart in air. Calculate the force between them.
Solution: Given: (q1 = 2 µC), (q2 = -3 µC), (r = 10 cm = 0.1m ), ( k = 9 × 109 N.m2/C2)
Magnitude of electric force:
\(\displaystyle F = \frac{k |q_1 q_2|}{r^2} \)
\(\displaystyle F = \frac{9 \times 10^9 \times |2 \times 10^{-6} \times -3 \times 10^{-6}|}{(0.1)^2} \)
\(\displaystyle F = \frac{9 \times 10^9 \times 6 \times 10^{-12}}{0.01} \)
\(\displaystyle F = \frac{54 \times 10^{-3}}{0.01} \)
\(\displaystyle F = 5400 \times 10^{-3} \)
\(\displaystyle F = 5.4 \, N \)
Therefore, the force between the charges is (5.4 N).
Question 1: Explain Coulomb’s Law and its mathematical representation.
Answer: Coulomb’s Law describes the electrostatic force between two point charges. It states that the force (F) between two charges (q1) and (q2) is directly proportional to the product of their magnitudes and inversely proportional to the square of the distance (r) between them. Mathematically, Coulomb’s Law is represented as:
\(\displaystyle F = k \frac{|q_1 q_2|}{r^2} \)
Question 2: Discuss the superposition principle in the context of Coulomb’s Law.
Answer: The superposition principle states that the net force on a charge due to multiple other charges is the vector sum of the individual forces exerted by each charge. In the context of Coulomb’s Law, this principle means that the total electrostatic force acting on a charge due to multiple charges is the sum of the forces exerted by each charge. Mathematically, if there are (n) charges (\(\displaystyle q_1, q_2, …, q_n \)) exerting forces \(\displaystyle F_1, F_2, …, F_n \) on a charge (Q), then the total force (Ftotal) on (Q is given by:
\(\displaystyle F_{\text{total}} = F_1 + F_2 + … + F_n \)
The superposition principle is essential for analyzing the electrostatic interactions in systems with multiple charges, enabling the determination of the net force and the resulting motion of charged particles.
FAQs
Can Coulomb’s Law be applied to point charges only?
No, Coulomb’s Law is not limited to point charges. It can be extended to apply to any pair of charges, regardless of their size or shape, as long as the distance between them is large compared to their sizes.
How does Coulomb’s Law change in a non-vacuum medium?
In a non-vacuum medium, Coulomb’s Law is modified by the permittivity of the medium. It is expressed as \(\displaystyle F = \frac{k \cdot q_1 \cdot q_2}{r^2} \cdot \frac{1}{\varepsilon} \), where \(\displaystyle\varepsilon \) is the permittivity of the medium.
Can Coulomb’s Law be applied to moving charges?
Coulomb’s Law is valid only for stationary charges. When dealing with moving charges, one must use the full form of electromagnetic force, which includes both electric and magnetic components, described by the Lorentz Force Law.
Is Coulomb’s Law only applicable to electrostatic situations?
Yes, Coulomb’s Law is primarily applicable in electrostatic situations where charges are at rest relative to each other. In dynamic scenarios involving moving charges, magnetic forces come into play along with electric forces.
How does Coulomb’s Law relate to Gauss’s Law?
Gauss’s Law is a fundamental electrostatic principle derived from Coulomb’s Law. While Coulomb’s Law provides the force between two charges, Gauss’s Law relates the net electric flux through a closed surface to the total charge enclosed by that surface.
Does Coulomb’s Law hold true for both positive and negative charges?
Yes, Coulomb’s Law holds for both positive and negative charges. The force between like charges is repulsive, while the force between unlike charges is attractive.
Can Coulomb’s Law be used in vector form?
Yes, Coulomb’s Law can be expressed in vector form as \(\displaystyle \vec{F} = \frac{k \cdot |q_1| \cdot |q_2|}{r^2} \cdot \hat{r} \), where \(\displaystyle\hat{r} \) is the unit vector in the direction from one charge to the other. This form helps in dealing with the directionality of the force.