Inductance

The story of inductance begins in the early 19th century with the observation of electromagnetic phenomena. Ancient civilizations were aware of static electricity and magnetism, but it was not until this period that the connection between electricity and magnetism began to be understood.

In 1831, Michael Faraday, a British scientist, conducted a series of experiments that led to the discovery of electromagnetic induction. He wrapped two wires around opposite sides of an iron ring and observed that when he passed a current through one wire, it induced a current in the other wire, even though they were not touching. This was the first demonstration of induced electromotive force due to a changing magnetic field.

At the same time, across the Atlantic, Joseph Henry, an American scientist, made similar discoveries independently. He observed that a current in one coil could induce a current in another nearby coil, even when they were not connected by a conductor.

The term “inductance” was coined by Oliver Heaviside in 1884. It was derived from the phrase “coefficient of self-induction” and was used to describe the property of a conductor to oppose changes in current flow through it.

The discoveries of Faraday and Henry set the stage for the development of many modern technologies, including transformers, electric motors, and much more. Their work showed that electricity and magnetism are two aspects of a single force: electromagnetism.

What is Inductance?

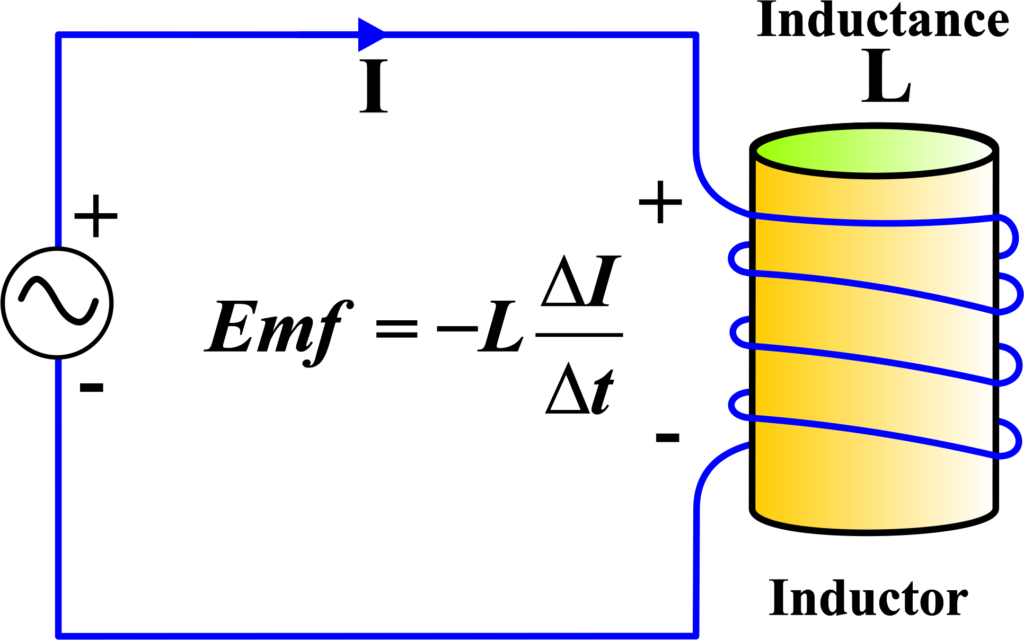
Inductance is the property of an electrical conductor by which a change in current flowing through it induces an electromotive force (emf) in both the conductor itself (self-inductance) and in any nearby conductors (mutual inductance). This is due to the magnetic field that is created around the conductor when an electric current flows through it.

Inductance is the tendency of an electrical conductor to oppose a change in the current flowing through it. This happens because a changing current creates a changing magnetic field, which in turn induces a voltage that opposes the original change in current. This effect is known as self-inductance when it occurs in a single coil and mutual inductance when it involves two adjacent coils.

Imagine you have a coil of wire connected to a battery. When you switch on the battery, an electric current starts to flow through the coil, creating a magnetic field around it. If the current changes—either increases or decreases—the magnetic field also changes. According to Faraday’s law of electromagnetic induction, a changing magnetic field will induce an emf in the coil. This induced emf is what we call inductance.

Unit: The unit of inductance is the Henry (H), named after the American scientist Joseph Henry. One Henry is defined as the amount of inductance required to induce one volt of electromotive force when the current changes at the rate of one ampere per second.

In essence, inductance is a measure of a circuit’s “electrical inertia.” Just as it takes force to change an object’s state of motion due to inertia, it takes electromotive force to change a circuit’s current due to inductance.

Factors Affecting Inductance

• Number of Turns in the Coil: The inductance is directly proportional to the number of turns in the coil. More turns mean more loops for the magnetic field to act on, which increases the magnetic flux and, consequently, the inductance.
• Coil Area: The inductance is also proportional to the cross-sectional area of the coil. A larger area allows more space for the magnetic field lines to pass through, which increases the magnetic flux linkage and the inductance.

• Coil Length: The length of the coil inversely affects inductance. A longer coil means the magnetic field lines have a longer path to travel, which can reduce the magnetic flux and the inductance.
• Permeability of the Medium: The medium in which the coil is placed affects the inductance. If the coil is in a medium with high permeability, the inductance will be higher due to the increased magnetic flux.
• Temperature: The inductance can change with temperature because the physical properties of the materials involved, like their permeability and resistance, can vary with temperature.
• Frequency of the Current: At higher frequencies, the inductance can change due to the skin effect, where the current tends to flow on the surface of the conductor, effectively reducing the cross-sectional area of the conductor and changing the inductance.
• Coil Geometry: The shape of the coil, whether it’s a simple loop, a solenoid, or a toroid, affects the inductance. Different geometries will have different levels of effectiveness in creating magnetic flux for a given current.

Types of Inductance

Inductance is a fundamental property of electrical circuits that describes the ability of a circuit element to store energy in the form of a magnetic field when an electric current flows through it. There are primarily two types of inductance:

• Self Inductance
• Mutual Inductance

Self Inductance

Self-inductance is a property of a coil (or any electrical conductor) that quantifies its opposition to changes in the electric current passing through it. This opposition is due to the electromotive force (emf) induced in the coil by its own changing magnetic field, hence the term ‘self’-inductance.

How does self-inductance occur?: Self-inductance is a phenomenon that occurs in electrical circuits when a current-carrying conductor, such as a coil, creates a magnetic field around itself. The key to understanding self-inductance is to explore the relationship between electricity and magnetism.

When an electric current flows through a conductor, it generates a magnetic field around it. The direction of this magnetic field is given by the right-hand rule. If the current changes (either increases or decreases), the magnetic field also changes. This is because the strength and direction of the magnetic field are directly related to the flow of current.

The magnetic field lines pass through the coil, creating what we call magnetic flux. The total magnetic flux linked with the coil depends on the strength of the magnetic field and the area of the coil. According to Faraday’s law, a change in magnetic flux through a circuit induces an electromotive force (emf) in the circuit. This is the fundamental principle behind the generation of electricity in generators.

As per Lenz’s law, the direction of the induced emf is such that it opposes the change in magnetic flux that produced it. This means that if the current in the coil increases, the induced emf will act to decrease it, and vice versa. The property of the coil that quantifies this behavior is called self-inductance. It is a measure of how much emf is induced for a given rate of change of current. The self-inductance of a coil is usually denoted by the letter ‘L’ and is measured in henries (H).

You can think of self-inductance as the electrical equivalent of inertia in mechanics. Just as inertia resists changes in the motion of an object, self-inductance resists changes in electrical current.

The Self-Inductance Formula: The induced emf E in a coil due to a change in current I over time can be expressed as:

\(\displaystyle E = -L \left( \frac{dI}{dt} \right) \)

where:

• E is the induced emf in volts,
• L is the self-inductance in Henries (H),
• \(\displaystyle\frac{dI}{dt}\) is the rate of change of current in amperes per second.

The negative sign indicates that the induced emf opposes the change in current, according to Lenz’s law.

Self-Inductance of a Solenoid

A solenoid is a long coil of wire. To calculate its self-inductance, we consider the number of turns N, the length l, the area of cross-section A, and the permeability of free space \(\displaystyle\mu_0 \) or the permeability of the core material μ if a core is present.

The self-inductance L of a solenoid is given by:

\(\displaystyle L = \frac{\mu N^2 A}{l} \)

Where:

• μ is the permeability of the core material (or μ₀ for air),
• N is the number of turns,
• A is the cross-sectional area,
• l is the length of the solenoid.

Self-Inductance Derivation

When an electric current ‘I’ flows through a coil, it generates a magnetic field around it. The magnetic flux Φ, which is the measure of the total magnetic field passing through the coil, is proportional to the current. This relationship is given by:

\(\displaystyle \Phi = L \times I \)

• Φ is the magnetic flux in webers (Wb),
• L is the self-inductance in henries (H),
• ‘I’ is the current in amperes (A).

According to Faraday’s law of electromagnetic induction, a change in magnetic flux through a coil induces an emf in the coil. The induced emf E is proportional to the rate of change of flux:

\(\displaystyle E = -\frac{d\Phi}{dt} \)

• E is the induced emf in volts (V),
• \(\displaystyle\frac{d\Phi}{dt} \) is the rate of change of magnetic flux.

Substituting the expression for ( \Phi ) from Step 1 into Faraday’s law, we get:

\(\displaystyle E = -L \frac{dI}{dt} \)

• \(\displaystyle\frac{dI}{dt} \) is the rate of change of current.

From the above equation, we can see that the self-inductance L can be defined as the ratio of the induced emf to the rate of change of current that caused it:

\(\displaystyle L = -\frac{E}{\frac{dI}{dt}} \)

The negative sign in Faraday’s law and the definition of L indicates that the induced emf opposes the change in current, according to Lenz’s law. Therefore, the final expression for self-inductance is often written as:

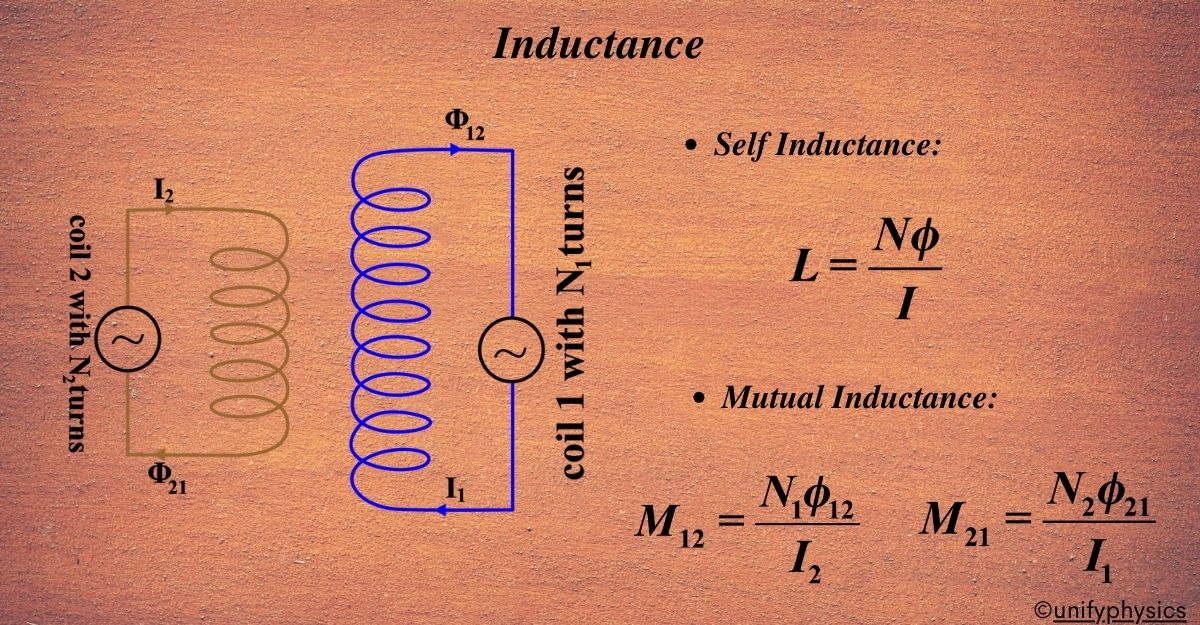
\(\displaystyle L = \frac{N\Phi}{I} \)

This formula shows that the self-inductance of a coil is directly proportional to the number of turns and the magnetic flux and inversely proportional to the current. The self-inductance also depends on the geometry of the coil and the magnetic permeability of the core material, as these factors affect the magnetic flux Φ.

Physical Analogy: Self-induction can be thought of as the electrical equivalent of inertia in mechanics. Just as inertia resists changes in the motion of an object, self-inductance resists changes in electrical current.

Inertia is the property of a body that resists any change in its state of motion. A body at rest tends to stay at rest, and a body in motion tends to stay in motion unless acted upon by an external force. This is known as Newton’s first law of motion.

Self-inductance in an electrical circuit is analogous to inertia in mechanics. Just as inertia resists changes in the motion of a body, self-inductance resists changes in the electric current flowing through a conductor. When the current in a coil changes, the magnetic field around the coil changes, which induces an electromotive force (emf) that opposes the change in current. This is known as Lenz’s law.

• Mass and Self-Inductance: Just as mass is the measure of inertia, self-inductance (( L )) is the measure of a coil’s tendency to oppose changes in current. A coil with higher self-inductance is like a body with more mass—it takes a greater force (or emf) to produce a change in current.
• Force and Electromotive Force: In mechanics, a force is required to change the velocity of a mass. In an electrical circuit, an electromotive force is required to change the current in a coil with self-inductance.
• Energy Storage: When you push a mass, you do work on it, and this work is stored as kinetic energy. Similarly, when you change the current in a coil, you do work against the induced emf, and this work is stored as magnetic potential energy. The energy stored in an inductor is given by:

\(\displaystyle W = \frac{1}{2} L I^2 \)

• W is the magnetic potential energy,
• L is the self-inductance,
• ‘I’ is the current.

Applications:

• Electromagnetic Relays: Self-inductance allows relays to act as switches in circuits, controlling the flow of current. They’re used in industrial automation, protection systems, and electronic control circuits.
• Electronic Filters: Inductors, exhibiting self-inductance, are used in filters to pass or block specific frequencies in audio systems, communication devices, and signal processing circuits.
• Charging and Discharging of Capacitors: Self-inductance influences the charging and discharging processes in circuits containing capacitors and inductors, essential in power supplies and voltage regulation circuits.
• Fluorescent Lamp Ballasts: Ballasts with inductive coils utilize self-inductance to regulate the current flow in fluorescent lamps, ensuring stable and efficient operation.
• Electromagnetic Actuators: Self-inductance powers electromagnetic actuators like solenoids and electromagnets, converting electrical energy into mechanical motion for various applications like door locks and automotive systems.

Mutual inductance

Mutual inductance is a concept in electromagnetism that describes the interaction between two coils when the current in one coil induces a voltage in the other. This is a key principle in the operation of transformers, motors, and many types of wireless communication devices.

How does self-inductance occur?: Imagine two coils, Coil 1 and Coil 2, placed close to each other without touching. Coil 1 is connected to a power source, and Coil 2 is connected to a device that can measure voltage, like a voltmeter.

Current in Coil 1: When a current (I₁) flows through Coil 1, it creates a magnetic field around it. Some of this magnetic field passes through coil 2, linking the two coils magnetically. The magnetic flux Φ₂₁ through coil 2 due to the current in coil 1 is proportional to (I₁). This can be expressed as:

\(\displaystyle \Phi_{21} = M_{21} \times I_1 \)

where M₂₁ is the mutual inductance of coil 2 with respect to coil 1.

Induced Voltage in Coil 2: According to Faraday’s law, a change in magnetic flux induces an electromotive force (emf). If the current (I₁) changes, it will induce a voltage \(\displaystyle\varepsilon_{21} \) in coil 2, which can be calculated as:

\(\displaystyle \varepsilon_{21} = -N_2 \frac{d\Phi_{21}}{dt} \)

where N₂ is the number of turns in coil 2 and \(\displaystyle\frac{d\Phi_{21}}{dt}\) is the rate of change of magnetic flux through coil 2. The induced voltage in coil 2 is directly proportional to the rate of change of current in coil 1. The constant of proportionality is the mutual inductance M₂₁, which is defined as:

\(\displaystyle M_{21} = \frac{N_2 \Phi_{21}}{I_1} \)

The same process applies if coil 2 has a changing current; it will induce a voltage in coil 1. The mutual inductance M₁₂ of coil 1 with respect to coil 2 is given by a similar formula. The unit of mutual inductance is the Henry (H), which is the same as that for self-inductance.

Final Formula for Mutual Inductance: The mutual inductance between two coils is often represented simply as ( M ), assuming the mutual inductance is the same in both directions due to the reciprocity theorem. The final formula for mutual inductance is:

\(\displaystyle M = \frac{N_2 \Phi_{21}}{I_1} = \frac{N_1 \Phi_{12}}{I_2} \)

• N₁ and N₂ are the number of turns in Coil 1 and Coil 2, respectively,
• Φ₁₂ and Φ₂₁ are the magnetic fluxes through Coil 1 and Coil 2 due to the currents in the other coils,
• I₁ and I₂ are the currents in Coil 1 and Coil 2.

This derivation shows how the mutual inductance between two coils can be calculated based on the number of turns and the magnetic flux created by currents in the coils. It’s a fundamental concept that explains how energy can be transferred between coils without physical contact.

Factors Affecting Mutual Inductance:

Mutual inductance is the measure of the ability of one coil to induce an electromotive force (EMF) in another nearby coil when the current in the first coil changes. Several factors influence mutual inductance:

• Number of Turns (N): Mutual inductance increases with the number of turns in the coils. More turns mean more magnetic flux linkage between the coils, leading to a higher mutual inductance. For example, if you increase the number of turns in either the primary or secondary coil of a transformer, the mutual inductance between them will increase.
• Geometry and Size of Coils: The physical arrangement and size of the coils affect mutual inductance. Coils with larger surface areas or closer proximity have stronger magnetic coupling and higher mutual inductance. For instance, if you place two coils closer together or wind them around a common core, the mutual inductance between them will increase due to better magnetic coupling.
• Relative Orientation: The orientation of the coils relative to each other also affects mutual inductance. Coils aligned parallel to each other have higher mutual inductance compared to coils oriented at an angle or perpendicular to each other. Aligning the coils so that their magnetic fields overlap maximizes mutual inductance.
• Permeability of the Medium: The permeability of the medium surrounding the coils influences mutual inductance. Materials with higher permeability, such as iron or ferrite cores, enhance magnetic coupling between the coils and increase mutual inductance. Using a ferromagnetic core in transformers improves mutual inductance by concentrating the magnetic flux and increasing magnetic coupling.
• Distance Between Coils: The distance between the coils affects mutual inductance. Closer proximity between the coils results in stronger magnetic coupling and higher mutual inductance while increasing the distance reduces mutual inductance. For example, in wireless power transfer systems, keeping the coils close together maximizes mutual inductance and improves energy transfer efficiency.

Applications of Mutual Inductance:

• Transformers: Mutual inductance is essential in transformers, which step up or step down voltage levels efficiently for power distribution and voltage regulation in electrical devices and grids.
• Wireless Power Transfer: Mutual inductance enables wireless power transfer systems, where energy is transmitted wirelessly between two coils, allowing devices like smartphones and medical implants to be powered without physical connections.
• Magnetic Sensors: Mutual inductance is used in magnetic sensors for object detection, speed sensing, and position control in industrial automation, automotive systems, and consumer electronics.
• RFID Systems: In RFID (Radio Frequency Identification) systems, mutual inductance is employed for contactless identification and tracking of objects in logistics, inventory management, access control, and electronic payment systems.
• Switching Power Supplies: Coupled inductors utilize mutual inductance in switching power supplies to improve efficiency, reduce electromagnetic interference, and provide isolation in high-frequency and high-power applications.

Mutual inductance is a fundamental concept that enables the operation of many modern electrical devices and systems.

Coefficient of Coupling for Mutual Inductance

The coefficient of coupling, denoted by k, measures how effectively two inductors induce voltage in each other. Imagine two dancers on a stage, each holding the end of a ribbon. As one dancer moves, the ribbon’s shape changes and the other dancer feels the pull. This connection between the two dancers through the ribbon is similar to the concept of mutual inductance in physics.

When we have two coils placed close to each other, and an electric current flows through one of them, it creates a magnetic field. This magnetic field can link with the second coil and induce a voltage in it. This is the basic idea of mutual inductance.

Now, not all of the magnetic field from the first coil will link with the second coil. The Coefficient of Coupling, denoted by (k), tells us what fraction of the magnetic field links the two coils. It’s a number between 0 and 1:

• If (k = 1), it means all the magnetic fields from the first coil are linked with the second coil’s perfect coupling.
• If (k = 0), it means no magnetic field from the first coil is affecting the second coil—no coupling.

The coefficient of coupling is given by the formula:

\(\displaystyle k = \frac{M}{\sqrt{L_1 L_2}} \)

• ( M ) is the mutual inductance between the two coils,
• (L₁) is the self-inductance of the first coil,
• (L₂) is the self-inductance of the second coil.

Let’s say we have two coils, Coil A and Coil B. Coil A has a self-inductance of 5 Henrys, and Coil B has a self-inductance of 3 Henrys. If the mutual inductance (M) between them is 1 Henry, the coefficient of coupling (k) would be:

\(\displaystyle k = \frac{1}{\sqrt{5 \times 3}} \)
\(\displaystyle k = \frac{1}{\sqrt{15}} \)
\(\displaystyle k \approx 0.258 \)

This means that approximately 25.8% of the magnetic field from Coil A is linked with Coil B.

The coefficient of coupling is important in designing circuits where inductors are used, like in transformers. A high coefficient of coupling means that the inductors are effectively transferring energy between them, which is crucial for efficient transformers.

In summary, the coefficient of coupling for mutual inductance is a measure of how well two coils are magnetically connected. It’s like the ribbon between our dancers: the stronger the connection, the more one dancer’s movements affect the other. In the world of physics, this translates to how effectively one coil’s magnetic field can induce a voltage in another coil.

Inductance of Series Coils

The inductance of series coils is an important concept in physics, especially when dealing with circuits that include multiple inductors. Imagine you have a row of batteries connected end-to-end. The total voltage you get from this setup is the sum of the individual voltages of each battery. Similarly, when you connect inductors in series (end-to-end), the total inductance is the sum of the individual inductances of each inductor.

When inductors are connected in series, they share the same current. As the current changes, each inductor will try to resist this change by inducing a voltage. The total voltage induced in the series is the sum of the voltages induced by each inductor. Since the voltage induced is a measure of inductance, the total inductance of the series is simply the sum of all the individual inductances.

The formula for calculating the total inductance (L_total) of a series of inductors is:

\(\displaystyle L_{total} = L_1 + L_2 + L_3 + … + L_n \)

where (L₁, L₂, L₃, …, L_n ) are the inductances of the individual inductors in the series.

Let’s say we have three inductors in series with inductances of 2 Henrys, 3 Henrys, and 5 Henrys. The total inductance (L_total) would be:

\(\displaystyle L_{total} = 2H + 3H + 5H = 10H \)

This straightforward addition applies only if the inductors are not magnetically coupled. If there is magnetic coupling between any of the inductors, the calculation becomes more complex because the mutual inductance must be considered.

When we connect two coils in a series, we’re essentially adding their inductances together, much like adding resistances in a series. However, there’s a twist when the coils are magnetically coupled.

Series Aiding: If the coils are arranged such that their magnetic fields aid each other (the fluxes are in the same direction), the equivalent inductance is given by:

\(\displaystyle L_{eq} = L_1 + L_2 + 2M \)

• (L_eq) is the equivalent inductance,
• (L₁) and (L₂) are the inductances of the individual coils,
• (M) is the mutual inductance.

This means that the total inductance is the sum of the individual inductances plus twice the mutual inductance because the fields are reinforcing each other.

Series Opposing: If the coils are arranged such that their magnetic fields oppose each other (the fluxes are in opposite directions), the equivalent inductance is given by:

\(\displaystyle L_{eq} = L_1 + L_2 – 2M \)

Here, we subtract twice the mutual inductance because the fields are working against each other, reducing the total inductance.

Think of two friends holding hands while running. If they run in the same direction (aiding), they can go faster together (higher inductance). If they run in opposite directions (opposing), they’ll slow each other down (lower inductance).

Understanding how series coils interact is crucial for designing circuits, especially in power systems and communication devices where inductors are used to filter signals or store energy.

In essence, the inductance of series coils depends on whether they are aiding or opposing each other. This concept helps us predict how a circuit will behave when the current changes, ensuring devices operate smoothly and efficiently. So, when you see coils lined up in a circuit, remember, their total inductance is influenced by how their magnetic fields interact!

Also Read: AC Generator

Inductances of Parallel Coils

For parallel coils, the total inductance is less than the smallest individual inductance if the coils are uncoupled. If they are coupled, the calculation becomes more complex, similar to resistors in parallel.

Imagine you have several pipes with water flowing through them, and these pipes come together at a single junction. The total flow through the junction is the sum of the flow through each pipe. Now, let’s think of electrical currents like water flow and inductors like pipes.

When inductors are connected in parallel, the total inductance is less than the smallest individual inductance among them. This might seem counterintuitive, so let’s explore why this happens.

Each inductor in a parallel circuit has the same voltage across it. When the current changes, each inductor will try to resist this change by inducing a voltage. However, because they are in parallel, the total current is divided among them. This division means that the change in current through each inductor is less than if it were alone, resulting in a smaller voltage change across each one.

The formula for calculating the total inductance (L_total) of parallel inductors is similar to that for resistors in parallel:

\(\displaystyle \frac{1}{L_{total}} = \frac{1}{L_1} + \frac{1}{L_2} + \frac{1}{L_3} + … + \frac{1}{L_n} \)

Let’s say we have two inductors in parallel, one with an inductance of 4 Henrys and the other with 6 Henrys. The total inductance (L_total) would be calculated as:

\(\displaystyle \frac{1}{L_{total}} = \frac{1}{4H} + \frac{1}{6H} \)
\(\displaystyle \frac{1}{L_{total}} = \frac{3}{12H} + \frac{2}{12H} \)
\(\displaystyle \frac{1}{L_{total}} = \frac{5}{12H} \)
\(\displaystyle L_{total} = \frac{12H}{5} \)
\(\displaystyle L_{total} = 2.4H \)

This calculation assumes there is no mutual inductance between the inductors. If there is mutual inductance, the total inductance could be affected by the amount of coupling between the coils.

Understanding the inductances of parallel coils is important for designing circuits where inductors are used to filter signals or store energy. It helps in predicting how a circuit will behave when the current changes, ensuring that devices operate smoothly and efficiently.

So, when inductors are connected in parallel, their total inductance decreases because the current’s path is divided among them, reducing the overall effect of any single inductor. It’s a bit like having multiple lanes on a highway; the more lanes you have, the less congested each lane is. Similarly, the more parallel paths for the current, the less “congested” each inductor is, resulting in lower total inductance.

When coils are connected in parallel, the total inductance is different from the sum of individual inductances. It’s similar to resistors in parallel, where the total resistance is less than the smallest individual resistor.

Equivalent Inductance of Coils in Parallel Aiding Connection:

In a parallel aiding connection, the coils’ magnetic fields help each other. This means that if one coil is generating a magnetic field in a certain direction, the other coil’s field is pointing the same way. The formula for the equivalent inductance (L_eq) when the coils are aiding each other is:

\(\displaystyle L_{eq} = \frac{L_1 \cdot L_2 – M^2}{L_1 + L_2 + 2M} \)

Equivalent Inductance of Coils in Parallel Opposing Connection:

In a parallel opposing connection, the coils’ magnetic fields oppose each other. If one coil generates a magnetic field in one direction, the other coil’s field is in the opposite direction. The formula for the equivalent inductance (L_eq) when the coils are opposing each other is:

\(\displaystyle L_{eq} = \frac{L_1 \cdot L_2 – M^2}{L_1 + L_2 – 2M} \)

Notice that the difference between aiding and opposing connections is the sign in front of the (2M) term.

Think of two teams playing tug-of-war. In an aiding connection, both teams are pulling in the same direction, which would be like adding their strengths together. In an opposing connection, the teams are pulling against each other, which would be like subtracting their strengths.

Understanding the inductances of parallel coils is important for designing circuits, especially where inductors are used to filter signals or store energy. Knowing whether coils aid or oppose each other helps in predicting how a circuit will behave when the current changes, ensuring that devices operate smoothly and efficiently.

In summary, the total inductance of parallel coils depends on whether they are aiding or opposing each other. So, when you see coils side by side in a circuit, remember, that their total inductance is influenced by their individual inductances and whether they’re working together or against each other!

Difference between Self and Mutual Inductance

Self-Inductance	Mutual Inductance
Self-inductance is the property of a coil that opposes the change in current flowing through it.	Mutual inductance is the property of two coils where a change in current in one coil induces an emf in the other coil.
Caused by a change in current within the same coil.	Caused by a change in current in a nearby coil.
The emf is induced in the coil itself due to its own changing current.	The emf is induced in one coil due to the changing current in the adjacent coil.
\(\displaystyle L = \frac{N\Phi}{I} \)	\(\displaystyle M = \frac{N_2\Phi_{21}}{I_1} \)
Measured in henries (H).	Also measured in henries (H).
Depends on the coil’s geometry, the number of turns, and the core material.	Depends on the relative position and orientation of the two coils, the distance between them, and the core material.
Used in single inductors, chokes, and other single-coil components.	Fundamental in transformers, wireless charging, and other systems where energy is transferred between coils.

Common Faults in Inductors

Inductors are components in electrical circuits that store energy in a magnetic field when electric current flows through them. However, like any other component, they can experience faults.

• Open Circuit: An open circuit fault occurs when the wire within the inductor breaks. This means that the electrical path is interrupted, and current cannot flow through the inductor at all. It’s like having a pipe with water flowing through it, and suddenly there’s a break in the pipe, stopping the flow.
• Short Circuit: A short circuit in an inductor happens when turns of the coil come into contact with each other, bypassing part of the coil. This reduces the total inductance because the current takes a “shortcut” and doesn’t flow through the entire coil. Imagine a race track where a section of the track is blocked, and racers take a shortcut, reducing the total distance they run.
• Core Losses: Core losses are related to the material of the core around which the coil is wound. If the core material becomes saturated, it cannot support any further increase in the magnetic field, which reduces the inductor’s effectiveness. Think of it like a sponge that’s fully soaked with water and can’t absorb anymore.
• Winding Losses: Winding losses occur due to the resistance of the wire used in the coil. As current flows through the wire, some energy is lost as heat. The longer the wire or the higher the resistance, the more significant these losses are. It’s similar to friction that heats up objects when they rub against each other.
• Insulation Breakdown: Insulation breakdown is when the insulation material that separates the turns of the coil degrades or is damaged. This can lead to short circuits between turns or even cause the inductor to fail. Imagine the insulation as the protective gear for a cyclist; if it fails, the cyclist can get hurt.
• Environmental Factors: Environmental factors such as temperature, humidity, and mechanical stress can also cause inductors to fail. For example, high temperatures can cause materials to expand and contract, leading to physical damage over time.

Examples

Example 1: A coil with self-inductance L = 0.2 H and resistance R = 20 Ω is connected to a 220 V AC source with a frequency of 50 Hz. Calculate the impedance of the coil.

Solution: Calculate Angular Frequency:

Angular frequency (ω ) is given by \(\displaystyle\omega = 2\pi f \).

Substituting the given values, we get \(\displaystyle\omega = 2\pi \times 50 = 100\pi \, \text{rad/s} \).

Calculate Impedance Z: The impedance ( Z ) of the coil is given by \(\displaystyle Z = \sqrt{R^2 + (\omega L)^2} \).

Substitute the given values into the formula:

\(\displaystyle Z = \sqrt{(20)^2 + (100\pi \times 0.2)^2} \)
\(\displaystyle Z = \sqrt{400 + 4000\pi^2} \)
\(\displaystyle Z \approx \sqrt{400 + 3926.99} \)
\(\displaystyle Z \approx \sqrt{4326.99} \)
\(\displaystyle Z \approx 65.80 \, \Omega \)

The impedance of the coil is approximately 65.80 Ω.

Example 2: Two coils ‘P’ and ‘S’ have self-inductances of 0.5 H and 0.2H respectively. When a current of 2A flowing through ‘P’ changes at a rate of 0.1 A/s an emf of 20V is induced in ‘S’. Calculate the mutual inductance between the two coils.

Solution: Given:

• Self-inductance of coil ‘P’, \(\displaystyle L_P = 0.5 \, \text{H} \)
• Self-inductance of coil ‘S’, \(\displaystyle L_S = 0.2 \, \text{H} \)
• Rate of change of current in coil ‘P’, \(\displaystyle \frac{dI_P}{dt} = 0.1 \, \text{A/s} \)
• Induced emf in coil ‘S’, \(\displaystyle V_S = 20 \, \text{V} \)

Using the formula for mutual inductance:

\(\displaystyle M = \frac{V_S}{\frac{dI_P}{dt}}\)

Substituting the given values:

\(\displaystyle M = \frac{20 \, \text{V}}{0.1 \, \text{A/s}} \)
\(\displaystyle M = 200 \, \text{H} \)

The calculated value for the mutual inductance ‘M’ is indeed 200 H.

Example 3: A coil with inductance L = 0.3 H and resistance R = 30 Ω is connected to a 100 V DC source. Calculate the energy stored in the magnetic field when the current becomes steady.

Solution: Calculate Steady Current ‘I’:

\(\displaystyle I = \frac{V}{R} = \frac{100}{30} = \frac{10}{3} \, \text{A} \)

Calculate Energy Stored W:

\(\displaystyle W = \frac{1}{2}LI^2 = \frac{1}{2} \times 0.3 \times \left(\frac{10}{3}\right)^2 = \frac{1}{2} \times 0.3 \times \frac{100}{9} = \frac{5}{3} \, \text{J} \)

Example 4: A coil has an inductance of 2H and resistance of 8Ω. It is connected to a battery supplying 12 V DC. After a long time, the battery is disconnected. Find the energy dissipated in the coil.

Solution: Given:

• Inductance L = 2 H
• Resistance R = 8 Ω
• DC voltage V = 12 V

Calculate Steady Current ‘I’ :

\(\displaystyle I = \frac{V}{R} = \frac{12}{8} = 1.5 \, \text{A} \)

Calculate Energy Dissipated W_d :

\(\displaystyle W_d = \frac{1}{2}LI^2 = \frac{1}{2} \times 2 \times (1.5)^2 = \frac{1}{2} \times 2 \times 2.25 = 2.25 \, \text{J} \)

Example 5: A coil with self-inductance L = 0.4 H and resistance R = 40 Ω is connected to a 220 V AC source with a frequency of 60Hz. Calculate the power factor of the coil.

Solution: Calculate Angular Frequency: Angular frequency Ω is given by

\(\displaystyle \omega = 2\pi f \).

Substituting the given values, we get

\(\displaystyle\omega = 2\pi \times 60 = 120\pi \, \text{rad/s} \).

Calculate Impedance Z: Impedance Z of the coil is given by

\(\displaystyle Z = \sqrt{R^2 + (\omega L)^2} \)

Substitute the given values into the formula:

\(\displaystyle Z = \sqrt{(40)^2 + (120\pi \times 0.4)^2} \)

\(\displaystyle Z = \sqrt{1600 + 57600\pi^2} \)

\(\displaystyle Z ≈ \sqrt{59265.97} \) \(\displaystyle Z ≈ 243.47 \, \Omega \)

Calculate Power Factor \(\displaystyle \cos \phi \). Power factor \(\displaystyle \cos \phi \) of the coil is given by

\(\displaystyle \cos \phi = \frac{R}{Z} \)

Substitute the calculated impedance into the formula:

\(\displaystyle\cos \phi = \frac{40}{243.47} \)

\(\displaystyle \cos \phi ≈ 0.1644 \)

The calculated value of the power factor is approximately 0.1644.

FAQs