The concept of AC (Alternating Current) voltage is rooted in the late 19th century during the “War of the Currents.” Thomas Edison was a staunch supporter of DC (Direct Current), which flows in one direction. However, Nikola Tesla and George Westinghouse championed the use of AC, which alternates direction. AC’s ability to be transmitted over long distances with less power loss compared to DC led to its widespread adoption. This was a pivotal moment in the history of electrical engineering, setting the stage for modern electrical power distribution systems.
Before we talk about applying AC voltage to a resistor, let’s understand what a resistor is. Imagine you’re trying to walk through a crowd. The more people there are, the harder it is to move forward. In an electrical circuit, a resistor acts like a crowd. It resists the flow of electric current, and this resistance is measured in ohms (Ω). The higher the resistance, the more it opposes the current.
Now, alternating voltage is like a dance of electric potential that changes its magnitude and direction with time. It’s not constant like DC voltage; it rises and falls, forming a wave-like pattern. This is why it’s called alternating—it switches between positive and negative values, providing a dynamic form of electricity that can power our homes and devices.
When we apply AC voltage to a resistor, the current through the resistor dances along with the voltage. They are in sync—when the voltage goes up, the current goes up; when the voltage goes down, the current goes down.
However, because AC voltage and current are not constant, we often use RMS (Root Mean Square) values to represent them. The RMS value is a type of average that allows us to compare AC to a constant DC value.
Resistor
A resistor is a component used in electrical circuits to limit or regulate the flow of electric current. It’s like a narrow path that slows down the flow of people walking through it. The resistance, measured in ohms (Ω), determines how much it restricts the current.
Imagine you’re playing a video game where you need to control the speed of your character. You have a joystick that lets you adjust how fast or slow you move—this is similar to what a resistor does in an electrical circuit. A resistor is a component that controls the flow of electrical current, much like how you control the speed of your character in the game.
A resistor is like a gatekeeper. It decides how much electrical current is allowed to pass through. If you have high resistance, less current flows, just like opening a tap slightly lets less water flow. If the resistance is low, more current can pass through, similar to opening the tap fully.
Resistors work by using the material they are made of to control the current. They can be made of various materials, such as carbon or metal alloys, which naturally resist the flow of electricity. This resistance turns electrical energy into heat, which is why resistors sometimes get warm when you use them.
Resistors are everywhere! They’re in your phone, controlling the brightness of your screen; in your car, managing the signals to the engine; and even in large power plants, where they help control the flow of electricity to entire cities.
When resistors do their job, they convert some of the electrical energy into heat. This is useful in some cases, like in a toaster where the heat cooks your bread. But in other cases, it’s just a byproduct, and engineers have to make sure the resistor doesn’t get too hot.
Alternating Voltage
Alternating voltage is like a swing that goes back and forth, changing its magnitude and direction with time. In technical terms, it’s a voltage that varies sinusoidally, meaning it follows a wave-like pattern over time.
Imagine you’re at the beach watching the waves come in and out. The water rises and falls, comes toward you, and then moves away. Alternating voltage is like those ocean waves. It’s a type of electrical voltage that rises and falls in a rhythm, changing its direction and magnitude over time.
Alternating voltage is created by alternating current (AC), which is like a dance where the electrical charges change direction back and forth. This is different from direct current (DC), where charges move in only one direction. The “alternating” part of AC means that the voltage switches from positive to negative and back again in a smooth, wave-like pattern.
Alternating voltage is used because it’s efficient for transporting electricity over long distances. It can easily be transformed into higher or lower voltages using transformers, which are handy for different stages of power distribution—from power plants to your home.
Every time you plug in your TV, turn on a light or use a kitchen appliance, you’re using alternating voltage. It’s the standard form of electrical supply in homes because it’s versatile and can power a wide range of devices.
The waveform of alternating voltage is sinusoidal, which means it looks like a smooth wave on a graph. The height of the wave represents the magnitude of the voltage, and the distance between waves represents the frequency—how many times the wave repeats in a second.
Mathematically, we can describe alternating voltage with the equation:
\(\displaystyle V(t) = V_m \sin(\omega t + \phi) \)
- V(t) is the voltage at time (t)
- Vm is the maximum voltage (the peak of the wave)
- (ω) is the angular frequency (how fast the wave oscillates)
- (Φ) is the phase angle
The beauty of alternating voltage is that it allows us to use electricity in so many ways. Without it, we wouldn’t have the convenience of household appliances or the ability to light up our homes at night.
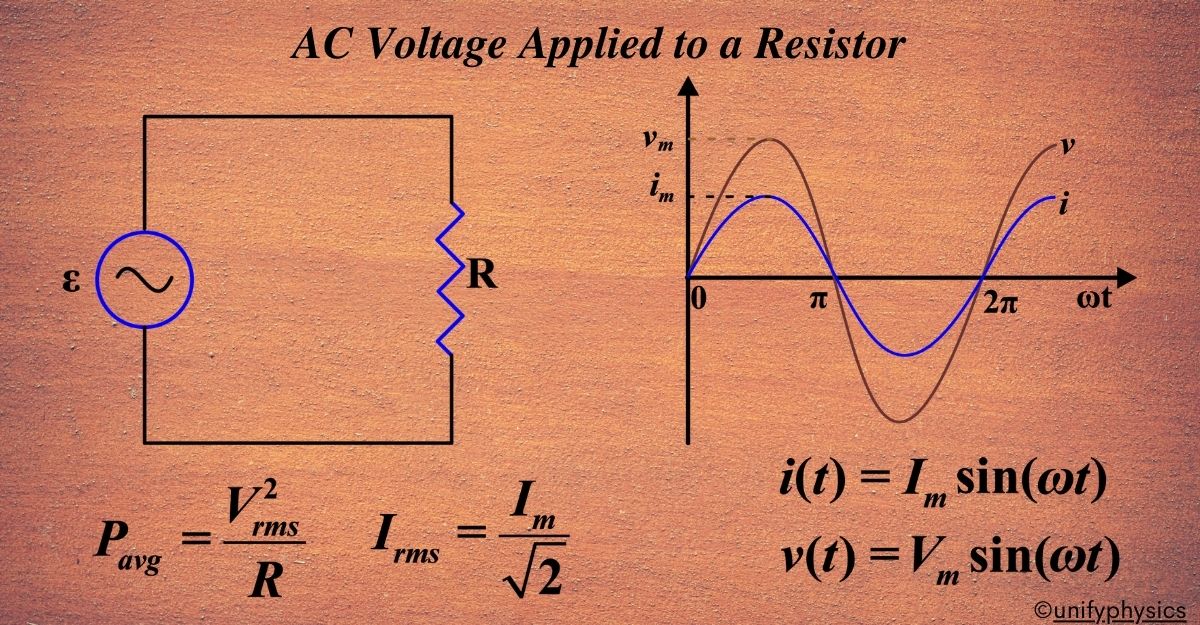
AC Voltage Applied to a Resistor
In AC circuits, the voltage and current are not constant; they change with time. When AC voltage is applied to a resistor, whether in series or parallel, the current through the resistor will change in sync with the voltage. This is because, according to Ohm’s law, the current (I) is directly proportional to the voltage (V) and inversely proportional to the resistance (R):
\(\displaystyle I = \frac{V}{R} \)
In an AC circuit, the voltage and current are often in phase when applied to a pure resistor, meaning they reach their maximum and minimum values at the same time. However, when other components like capacitors or inductors are involved, the phase relationship can change.
Think of AC voltage like a swing going back and forth. Sometimes it pushes you forward, sometimes backward. Now, imagine a resistor as a narrow path. When the swing pushes you forward, you try to walk along the path. It’s tough because the path is narrow and slows you down. This is like when the AC voltage is positive, pushing electric charge through the resistor.
Then, the swing pulls you back. Now, you try to walk in the opposite direction along the same narrow path. Again, it’s tough because of the resistance. This is like when the AC voltage is negative, pushing electric charge in the opposite direction through the resistor. So, when you put AC voltage through a resistor, it’s like a constant push and pull, making electricity flow back and forth, and the resistor gets hot because it’s hard for the electricity to move through it.
Imagine you have a resistor, and you connect it to a source that provides AC voltage. Unlike DC (Direct Current) voltage, which is constant and unidirectional, AC voltage changes its magnitude and direction periodically. This means the voltage alternates between positive and negative values in a sinusoidal fashion.
Now, the voltage across the resistor at any given time t can be expressed as:
\(\displaystyle v(t) = V_m \sin(\omega t) \)
Here, Vm is the maximum voltage (also known as the amplitude), and ω is the angular frequency of the AC source.
According to Ohm’s law, the current i through the resistor is directly proportional to the voltage v(t) applied across it. So, the current at any time t can be calculated using the formula:
\(\displaystyle i(t) = \frac{v(t)}{R} \)
Where R is the resistance of the resistor. Substituting the expression for v(t) we get:
\(\displaystyle i(t) = \frac{V_m}{R} \sin(\omega t) \)
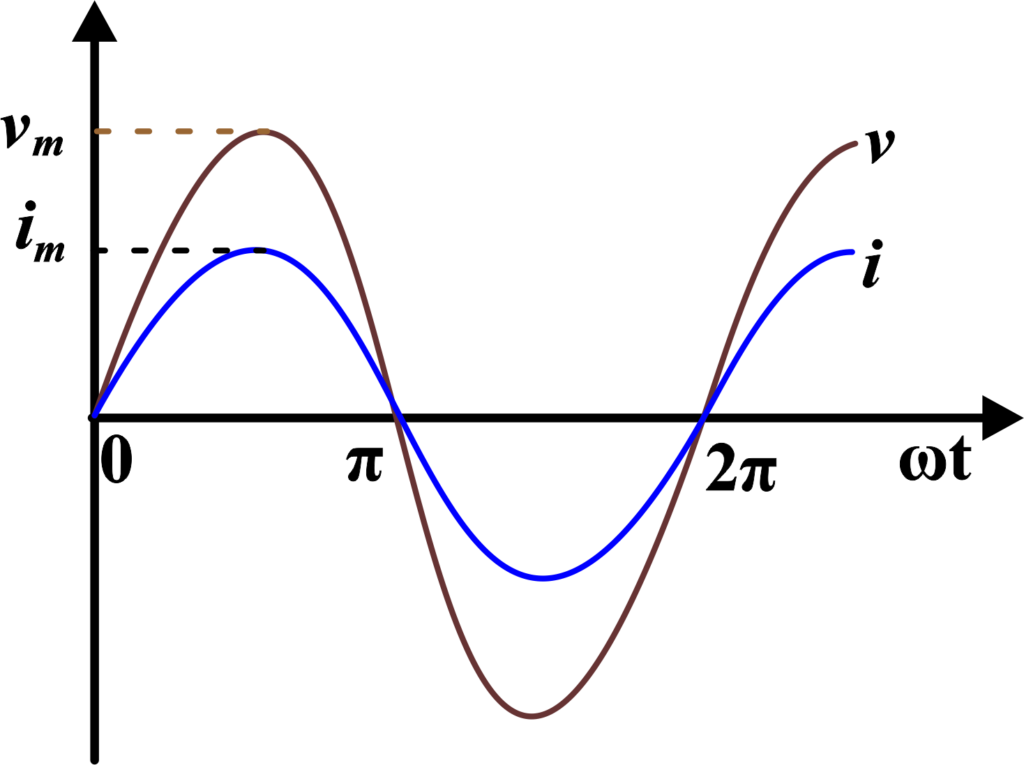
This equation shows that the current also varies sinusoidally with time and has the same frequency as the voltage. Moreover, the voltage and current are in phase, meaning they reach their maximum and minimum values at the same time.
The power P dissipated in the resistor can be found using the formula:
\(\displaystyle P(t) = i^2(t) R \)
However, since the current is alternating, we often use the RMS (Root Mean Square) value to express an equivalent DC value for AC. The RMS value of the current is given by:
\(\displaystyle I_{RMS} = \frac{I_m}{\sqrt{2}} \)
Where ( Im ) is the maximum current. The average power over a cycle is then:
\(\displaystyle P_{avg} = I_{RMS}^2 R \)
AC Voltage Applied to a Resistor in Series: When resistors are connected in series in an AC circuit, they’re like a line of people holding hands, where the electric current has to pass through each person one by one. The voltage drop across each resistor is like the energy each person uses to hold on.
To find the total voltage drop across the series, you add up the energy used by each person. Mathematically, if you have resistors (\(\displaystyle R_1, R_2, \ldots, R_n \)) connected in series, the total voltage (Vtotal) is the sum of the individual voltage drops:
\(\displaystyle V_{total} = V_1 + V_2 + \ldots + V_n \)
AC Voltage Applied to a Resistor in Parallel: In a parallel connection, resistors are like multiple paths in a park. People (electric current) can choose different paths, and each path has its flow of people. The current across each branch (path) is like the number of people walking on it.
To find the total current in the circuit, you count all the people walking on all paths. For resistors (\(\displaystyle R_1, R_2, \ldots, R_n \)) in parallel, the total current (Itotal) is the sum of the currents through each resistor:
\(\displaystyle I_{total} = I_1 + I_2 + \ldots + I_n \)
RMS Value
For AC voltage applied to a resistor, the RMS value tells us the equivalent DC voltage that would produce the same amount of heat in the resistor. In other words, it’s a way of comparing the heating effect of AC voltage to that of DC voltage.
So, when we say the RMS value of an AC voltage is, let’s say, 10 volts, it means that if you applied a steady DC voltage of 10 volts to the same resistor, it would generate the same amount of heat as the AC voltage does when it’s fluctuating.
The RMS value is a statistical measure of the magnitude of a varying quantity and is used to compare the values of alternating current (AC) and direct current (DC). It provides an equivalent value that would have the same effect as a DC value.
For an AC current that varies sinusoidally with time, the instantaneous current can be expressed as:
\(\displaystyle i(t) = I_m \sin(\omega t) \)
Where:
- i(t) is the instantaneous current at time t ,
- Im is the maximum current, and
- ω is the angular frequency.
The RMS value of the current is defined as the square root of the average of the squares of the instantaneous values over one complete cycle. Mathematically, it is represented as:
\(\displaystyle I_{RMS} = \sqrt{\frac{1}{T} \int_{0}^{T} [i(t)]^2 dt} \)
Where T is the period of the cycle. Substituting the expression for i(t) into the integral, we get:
\(\displaystyle I_{RMS} = \sqrt{\frac{1}{T} \int_{0}^{T} [I_m \sin(\omega t)]^2 dt} \)
Simplifying the integral, we have:
\(\displaystyle I_{RMS} = \sqrt{\frac{1}{T} \int_{0}^{T} I_m^2 \sin^2(\omega t) dt} \)
Using the trigonometric identity \(\displaystyle\sin^2(x) = \frac{1}{2} – \frac{1}{2} \cos(2x) \), the integral becomes:
\(\displaystyle I_{RMS} = \sqrt{\frac{1}{T} \int_{0}^{T} \frac{I_m^2}{2} – \frac{I_m^2}{2} \cos(2\omega t) dt} \)
The integral of \(\displaystyle \cos(2\omega t) \) over one period is zero, so we are left with:
\(\displaystyle I_{RMS} = \sqrt{\frac{1}{T} \int_{0}^{T} \frac{I_m^2}{2} dt} \)
This simplifies to:
\(\displaystyle I_{RMS} = \sqrt{\frac{I_m^2}{2}} \)
This gives us the final expression for the RMS value of the current:
\(\displaystyle \boldsymbol{ I_{RMS} = \frac{I_m}{\sqrt{2}}}\)
So, the RMS value of a sinusoidally varying current (or voltage) is equal to the maximum value divided by the square root of two. This RMS value is very useful because it allows us to calculate the power consumed by AC circuits as if they were DC circuits.
the power dissipated in the resistor
Now, think about a resistor in an electric circuit. A resistor is like a tiny, electrical obstacle course for the electricity flowing through the circuit. As the electricity passes through the resistor, it faces resistance, just like trying to walk through thick mud. This resistance turns some of the electrical energy into heat energy.
So the power dissipated in the resistor is the amount of energy that the resistor turns into heat. It’s like when you use a toaster or a hairdryer, they get warm because they’re turning electrical energy into heat.
In simple terms, when electricity flows through a resistor, it gets slowed down and some of its energy is turned into heat. The power dissipated in the resistor is the amount of heat produced.
The power dissipated in a resistor can be calculated using the formula:
\(\displaystyle P(t) = v(t) \cdot i(t) \)
Where P(t) is the instantaneous power, v(t) is the instantaneous voltage, and i(t) is the instantaneous current. For an AC circuit, the voltage and current are sinusoidal and can be expressed as:
\(\displaystyle v(t) = V_m \sin(\omega t) \)
\(\displaystyle i(t) = I_m \sin(\omega t) \)
Here, Vm and Im are the maximum (peak) values of the voltage and current, respectively, and ω is the angular frequency. Substituting these expressions into the power formula, we get:
\(\displaystyle P(t) = V_m \sin(\omega t) \cdot I_m \sin(\omega t) \)
Using the trigonometric identity for the product of sines:
\(\displaystyle \sin A \sin B = \frac{1}{2}[\cos(A – B) – \cos(A + B)] \)
We can rewrite the power as:
\(\displaystyle P(t) = \frac{V_m I_m}{2}[\cos(0) – \cos(2\omega t)] \)
Since \(\displaystyle \cos(0) = 1 \), the equation simplifies to:
\(\displaystyle P(t) = \frac{V_m I_m}{2}[1 – \cos(2\omega t)] \)
The average power over a complete cycle is the power that is actually used or dissipated in the resistor. To find this, we take the average of ( P(t) ) over one period ( T ):
\(\displaystyle P_{avg} = \frac{1}{T} \int_{0}^{T} P(t) dt \)
The average value of \(\displaystyle \cos(2\omega t) \) over a complete cycle is zero, so the average power becomes:
\(\displaystyle P_{avg} = \frac{V_m I_m}{2} \)
Now, we know that the RMS values of voltage and current are related to their maximum values by:
\(\displaystyle V_{RMS} = \frac{V_m}{\sqrt{2}} \)
\(\displaystyle I_{RMS} = \frac{I_m}{\sqrt{2}} \)
Substituting these into the average power formula, we get:
\(\displaystyle\boldsymbol{ P_{avg} = \frac{V_{RMS}^2}{R}} \)
Where R is the resistance of the resistor.
So, the average power dissipated in a resistor in an AC circuit is equal to the square of the RMS voltage divided by the resistance. This is the power that would be dissipated if the same value of DC voltage were applied to the resistor. It’s a crucial concept for understanding how much energy is used in AC circuits.
RMS (Root Mean Square) voltage
For AC voltage, the RMS value tells us the equivalent DC voltage that would produce the same amount of power in a resistor. In simpler terms, it’s a way of understanding the “average” strength of AC voltage by comparing it to an equivalent steady DC voltage.
So, when we say the RMS value of an AC voltage is, let’s say, 10 volts, it means that if you applied a steady DC voltage of 10 volts to the same resistor, it would generate the same amount of power as the AC voltage does when it’s fluctuating.
The RMS value is a form of average that is used to represent the effective value of an alternating current or voltage. It is particularly useful because it gives us a value that can directly be compared to a DC (Direct Current) value to calculate power.
For a sinusoidal AC voltage, the instantaneous voltage at any time t can be expressed as:
\(\displaystyle v(t) = V_m \sin(\omega t) \)
The RMS voltage is defined as the square root of the average of the square of the instantaneous voltage over one complete cycle. Mathematically, this is represented as:
\(\displaystyle V_{RMS} = \sqrt{\frac{1}{T} \int_{0}^{T} [v(t)]^2 dt} \)
Where T is the period of the cycle. Substituting the expression for v(t) into the integral, we get:
\(\displaystyle V_{RMS} = \sqrt{\frac{1}{T} \int_{0}^{T} [V_m \sin(\omega t)]^2 dt} \)
Simplifying the integral, we have:
\(\displaystyle V_{RMS} = \sqrt{\frac{1}{T} \int_{0}^{T} V_m^2 \sin^2(\omega t) dt} \)
Using the trigonometric identity \(\displaystyle \sin^2(x) = \frac{1}{2} – \frac{1}{2} \cos(2x) \), the integral becomes:
\(\displaystyle V_{RMS} = \sqrt{\frac{1}{T} \int_{0}^{T} \frac{V_m^2}{2} – \frac{V_m^2}{2} \cos(2\omega t) dt} \)
The integral of \(\displaystyle \cos(2\omega t)\) over one period is zero, so we are left with:
\(\displaystyle V_{RMS} = \sqrt{\frac{1}{T} \int_{0}^{T} \frac{V_m^2}{2} dt} \)
This simplifies to:
\(\displaystyle V_{RMS} = \sqrt{\frac{V_m^2}{2}} \)
This gives us the final expression for the RMS voltage:
\(\displaystyle \boldsymbol{ V_{RMS} = \frac{V_m}{\sqrt{2}} }\)
So, the RMS voltage of a sinusoidally varying voltage is equal to the peak voltage divided by the square root of two. This RMS value is crucial for calculating the power in AC circuits as if they were DC circuits, allowing for easier analysis and understanding of these systems.
Also Read: Representation of AC Current And Voltage By Phasor Diagram
Examples
Example 1: An AC voltage of 10 V is applied across a resistor of 5 Ω in an electrical circuit. What is the current passing through the resistor?
Solution: We can use Ohm’s Law to find the current (( I )) passing through the resistor, which states: V = IR
Rearranging the formula to solve for I :
\(\displaystyle I = \frac{V}{R} \)
Substituting the given values:
\(\displaystyle I = \frac{10}{5} \)
\(\displaystyle I = 2 \, \text{A} \)
Therefore, the current passing through the resistor is (2 \, \text{A}).
Example 2: A sinusoidal voltage of amplitude 20 V is applied across a resistor of 10 Ω. Calculate the maximum current through the resistor.
Solution:
In an AC circuit, the maximum current Imax through a resistor is given by Ohm’s Law as:
\(\displaystyle I_{\text{max}} = \frac{V_{\text{max}}}{R} \)
Substituting the given values:
\(\displaystyle I_{\text{max}} = \frac{20}{10} \)
\(\displaystyle I_{\text{max}} = 2 \, \text{A} \)
Therefore, the maximum current through the resistor is 2 A.
Example 3: An AC voltage source with a peak voltage of 15 V is connected across a 3 Ω resistor. Determine the RMS current in the circuit.
Solution: In an AC circuit, the RMS (Root Mean Square) current IRMS is related to the peak voltage Vpeak and the resistance R by the formula:
\(\displaystyle I_{\text{RMS}} = \frac{V_{\text{peak}}}{\sqrt{2} R} \)
Substituting the given values:
\(\displaystyle I_{\text{RMS}} = \frac{15}{\sqrt{2} \times 3} \approx \frac{15}{\sqrt{6}} \)
To simplify the expression, rationalize the denominator:
\(\displaystyle I_{\text{RMS}} \approx \frac{15\sqrt{6}}{6} \)
Therefore, the RMS current in the circuit is approximate \(\displaystyle\frac{5\sqrt{6}}{2} \, \text{A} \).
Example 4: An AC voltage source with an effective voltage of 12 V is connected across a 6Ω resistor. Find the power dissipated in the resistor.
Solution: The power P dissipated in a resistor in an AC circuit is given by the formula:
\(\displaystyle P = I_{\text{RMS}}^2 R \)
To find IRMS, we use Ohm’s Law:
\(\displaystyle I_{\text{RMS}} = \frac{V_{\text{eff}}}{R} = \frac{12}{6} = 2 \, \text{A} ] \)
Substituting IRMS into the power formula:
\(\displaystyle P = (2)^2 \times 6 = 4 \times 6 = 24 \, \text{W} \)
Therefore, the power dissipated in the resistor is 24 W.
Example 5: An AC voltage source with an effective voltage of 20 V is connected across a resistor. If the power dissipated in the resistor is 100 W, determine the resistance of the resistor.
Solution: Power Dissipated P= 100 W.
To find the resistance R of the resistor. We know that the power dissipated in a resistor in an AC circuit is given by the formula:
\(\displaystyle P = I_{\text{RMS}}^2 R \)
Given that \(\displaystyle I_{\text{RMS}} = \frac{V_{\text{eff}}}{R} )\), where Veff is the effective voltage, we can substitute the values into the power formula:
\(\displaystyle P = \left( \frac{V_{\text{eff}}}{R} \right)^2 R \)
Solving for R:
\(\displaystyle R = \frac{V_{\text{eff}}^2}{P} \)
Substituting the given values:
\(\displaystyle R = \frac{(20)^2}{100} = \frac{400}{100} = 4 \, \Omega \)
Therefore, the resistance of the resistor is 4 Ω.
FAQs
What happens when an AC voltage is applied to a resistor?
When an AC voltage is applied to a resistor, the current through the resistor varies sinusoidally with the same frequency as the applied voltage. The voltage and current are in phase, meaning they reach their maximum and minimum values simultaneously.
How does the current through a resistor behave when subjected to AC voltage?
The current through a resistor subjected to AC voltage behaves in a sinusoidal manner, mirroring the applied voltage. The amplitude of the current depends on the amplitude of the voltage and the resistance value.
What is the phase relationship between voltage and current in an AC circuit with only a resistor?
In an AC circuit with only a resistor, the voltage and current are in phase. This means the peaks and zero crossings of the voltage waveform occur simultaneously with the peaks and zero crossings of the current waveform.
How is the power dissipated in a resistor connected to an AC voltage source?
The power dissipated in a resistor connected to an AC voltage source is continuously converted into heat. The average power dissipation over a complete cycle is proportional to the square of the RMS (root mean square) values of the voltage or current.
What is the effect of frequency on the current through a resistor when AC voltage is applied?
The frequency of the AC voltage does not affect the current through a resistor in terms of amplitude, as the resistor’s opposition to current flow (resistance) is independent of frequency. However, the current will still vary sinusoidally with the same frequency as the applied voltage.
Can a resistor affect the shape of the AC voltage waveform?
No, a resistor does not affect the shape of the AC voltage waveform. The voltage waveform remains sinusoidal, and the current waveform follows the same sinusoidal shape without distortion when passing through a resistor.
What happens to the power factor in a purely resistive AC circuit?
In a purely resistive AC circuit, the power factor is 1 (or unity). This is because the voltage and current are in phase, resulting in the most efficient power transfer where all the power supplied by the source is dissipated as heat in the resistor.