The story of the Ideal Gas Law is a tale of the discovery and the unification of several individual gas laws. It began in the 17th century with Boyle’s Law, discovered by Robert Boyle, which found that pressure and volume are inversely proportional in a gas at a constant temperature. Then, in the 18th century, Charles’s Law came into the picture, thanks to Jacques Charles, who observed that the volume of a gas is directly proportional to its temperature at constant pressure.
Fast forward to the early 19th century, and we have Gay-Lussac’s Law, which states that the pressure of a gas is directly proportional to its temperature at constant volume. Meanwhile, Avogadro’s Law, proposed by Amedeo Avogadro, established that equal volumes of gases, at the same temperature and pressure, contain an equal number of molecules.
The real breakthrough came in 1834 when French engineer and physicist Benoît Paul Émile Clapeyron combined these individual laws into one comprehensive equation, now known as the Ideal Gas Law. This was a significant moment in the history of thermodynamics and physical chemistry, as it provided a single, unified formula that could predict the behavior of gases under various conditions.
Clapeyron’s work laid the foundation for future scientists like August Krönig and Rudolf Clausius, who further developed the kinetic theory of gases, providing a molecular interpretation of the Ideal Gas Law in the mid-19th century.
The Ideal Gas Law is a cornerstone of physical science because it’s a simple yet powerful tool that helps us understand the fundamental behavior of gases. It’s an excellent example of how scientific knowledge evolves, building on the discoveries of those who came before to develop a deeper understanding of the natural world.
What is the Ideal Gas Law?
The Ideal Gas Law describes how gases behave under various conditions of pressure, volume, and temperature. It assumes that the gas particles are in constant, random motion and that they do not interact with each other. The Ideal Gas Law is a fundamental principle in physics and chemistry that describes the behavior of an ideal gas. An ideal gas is a hypothetical gas that perfectly follows certain rules:
- The molecules of an ideal gas do not attract or repel each other. The only interactions are elastic collisions, either with each other or with the walls of their container.
- The molecules are considered to be point particles, meaning they have no volume of their own. The space the gas occupies is due to the motion of these point particles spreading out.
Now, why do we use the term “ideal”? Because in reality, no gas follows these rules perfectly. However, many gases behave closely enough to this ideal model that it becomes extremely useful for making predictions about gas behavior, especially at room temperature and near atmospheric pressure.
The Ideal Gas Equation
The Ideal Gas Law is expressed by the equation PV = nRT, where:
- P stands for the pressure of the gas,
- V is the volume the gas occupies,
- T is the temperature of the gas,
- n is the number of moles of the gas (a measure of the quantity of gas),
- R is the ideal gas constant, which is the same for all gases.
Imagine you have a balloon filled with air (which we’ll think of as an ideal gas for simplicity). If you squeeze the balloon (increasing pressure, P), the balloon gets smaller (decreasing volume, V). If you heat the balloon, the air inside gets warmer (increasing temperature, T), and the balloon expands (increasing volume, V). Let’s understand what the equation tells us:
- If you increase the pressure (P) on a gas, its volume (V) will decrease, assuming the temperature (T) and the amount of gas (n) stay the same. This is known as Boyle’s Law.
- If you heat a gas, increasing its temperature (T), its volume (V) will increase if the pressure (P) and the amount of gas (n) are constant. This is Charles’s Law.
- If you add more gas, increasing the number of moles (n), the volume (V) will also increase if the pressure (P) and temperature (T) are constant. This is Avogadro’s Law.
The Ideal Gas Law combines these three separate laws into one general law that applies to all ideal gases. It’s like a recipe that tells us how the ingredients of pressure, volume, temperature, and quantity mix together to describe the state of a gas.
We call it “ideal” because it assumes the gas particles are tiny dots that don’t attract or repel each other and don’t take up any space themselves. It’s an ideal situation that doesn’t exactly happen in real life, but it’s very close to how real gases behave most of the time.
Understanding the Ideal Gas Law is crucial because it helps us predict how gases will behave in different situations, like when inflating a balloon, using a gas stove, or even when studying the atmosphere. This equation is for things like how much oxygen is needed for astronauts in space, or how to design airbags that inflate properly in cars.
Derivation of the Ideal Gas Equation
The Ideal Gas Equation is a cornerstone of thermodynamics and it combines three historical gas laws: Boyle’s Law, Charles’s Law, and Avogadro’s Law.
Boyle’s Law
Boyle’s Law states that for a given mass of gas at a constant temperature, the pressure of the gas is inversely proportional to its volume. This means that if you increase the volume, the pressure decreases, and vice versa, as long as the temperature remains constant. Mathematically, this is expressed as:
\(\displaystyle\begin{equation}\label{eqn:1}\boxed{\boldsymbol{P \propto \frac{1}{V} \quad }} \end{equation}\hspace{1cm}\text{(at constant n and T)}\)
To convert the proportionality into an equation, we introduce a proportionality constant (( k )). This gives us:
\(\displaystyle P = k \times \frac{1}{V} \)
By rearranging the equation, we get the product of pressure and volume equal to a constant:
\(\displaystyle PV = k \)
Now, let’s consider the gas at two different states, state 1 with pressure (P1) and volume (V1), and state 2 with pressure (P2) and volume (V2). According to Boyle’s Law, the product of pressure and volume at each state will be equal to the same constant (k):
\(\displaystyle P_{1}V_{1} = k \) \(\displaystyle \hspace{1cm}\) and \(\displaystyle \hspace{1cm}\) \(\displaystyle P_{2}V_{2} = k \)
Since both (P1V1 ) and ( P2V2 ) are equal to (k, they are equal to each other:
\(\displaystyle P_{1}V_{1} = P_{2}V_{2} \)
This is the final expression of Boyle’s Law. It tells us that for a given mass of gas at constant temperature, the initial and final products of pressure and volume are equal.
Imagine a syringe filled with air. If you pull the plunger back, you’re increasing the volume inside the syringe. According to Boyle’s Law, the pressure of the air inside the syringe will decrease. If you push the plunger in, reducing the volume, the pressure of the air will increase.
Boyle’s Law is important because it helps us understand how gases will behave in different situations. For example, it’s used in designing syringes, understanding how our lungs work when we breathe, and even in scuba diving to prevent decompression sickness.
Boyle’s Law is all about the push and pull between pressure and volume. When one goes up, the other goes down, as long as the temperature stays the same. It’s a simple yet powerful concept that explains a lot about the world around us!
Charles’s Law
Charles’s Law states that at constant pressure, the volume of a fixed mass of a dry gas is directly proportional to its absolute temperature. This means that if you increase the temperature of the gas, its volume will increase proportionally, and if you decrease the temperature, the volume will decrease proportionally. We can write this as:
\(\displaystyle\begin{equation}\label{eqn:2}\boxed{\boldsymbol{V \propto T \quad }} \end{equation}\hspace{1cm} \text{(at constant n and P)} \)
To convert the proportionality into an equation, we introduce a proportionality constant (k). This gives us:
\(\displaystyle V = k \times T \)
Now, let’s consider the gas at two different states, state 1 with volume (V1) and temperature (T1), and state 2 with volume (V2) and temperature (T2). According to Charles’s Law, the ratio of volume to temperature for each state will be equal to the same constant (k):
\(\displaystyle \frac{V_1}{T_1} = k \) \(\displaystyle \hspace{1cm}\) and \(\displaystyle\hspace{1cm}\) \(\displaystyle \frac{V_2}{T_2} = k \)
Since both \(\displaystyle\frac{V_1}{T_1} \) and \(\displaystyle\frac{V_2}{T_2}\) are equal to (k), they are equal to each other:
\(\displaystyle \frac{V_1}{T_1} = \frac{V_2}{T_2} \)
This is the final expression of Charles’s Law. It tells us that for a given mass of gas at constant pressure, the ratio of the volume to the temperature (in Kelvin) is constant. It’s important to remember that the temperatures in this equation must be in absolute units (Kelvin), not Celsius or Fahrenheit.
Imagine a balloon on a cold day. The balloon is limp because the cold temperature makes the gas inside take up less space. If you take the same balloon into a warm room, it expands and becomes firm. This happens because the gas particles move faster and spread out more when they’re warmer, taking up more space.
Charles’s Law is important in everyday life. It explains why hot air balloons rise and why car tires can become overinflated in the summer. It’s also crucial in many scientific calculations and applications, like determining the correct gas volumes in chemical reactions.
Charles’s Law is a simple yet powerful concept that helps us predict how the volume of a gas will change with temperature. It’s a fundamental part of understanding how gases behave and is a key piece of the puzzle in the study of thermodynamics.
Avogadro’s Law
Avogadro’s Law tells us that at a constant temperature and pressure, the volume of a gas is directly proportional to the number of moles of the gas. In equation form, it looks like this:
\(\displaystyle\begin{equation}\label{eqn:3}\boxed{\boldsymbol{ V \propto n \quad }} \end{equation}\hspace{1cm} \text{(at constant P and T)}\)
We begin with the Ideal Gas Equation, which relates the pressure, volume, temperature, and number of moles of a gas:
\(\displaystyle PV = nRT \)
Here, (P) is the pressure, (V) is the volume, (n) is the number of moles, (R) is the ideal gas constant, and (T) is the temperature. To focus on the relationship between volume and the number of moles, we rearrange the equation to solve for (V):
\(\displaystyle V = \frac{nRT}{P} \)
Since Avogadro’s Law holds temperature and pressure constant, (RT/P) is a constant value. We can call this constant (k):
\(\displaystyle V = nk \)
Now, we express the direct proportionality between volume and the number of moles:
\(\displaystyle V \propto n \)
Consider two different states of the gas, state 1 with volume (V1) and number of moles (n1), and state 2 with volume (V2) and number of moles (n2). According to Avogadro’s Law, the ratio of volume to the number of moles for each state will be equal:
\(\displaystyle \frac{V_1}{n_1} = k \) \(\displaystyle \hspace{1cm}\) and \(\displaystyle \hspace{1cm}\) \(\displaystyle \frac{V_2}{n_2} = k \)
Since both \(\displaystyle\frac{V_1}{n_1} \) and \(\displaystyle \frac{V_2}{n_2} \) are equal to (k), they are equal to each other:
\(\displaystyle \frac{V_1}{n_1} = \frac{V_2}{n_2} \)
This is the final expression of Avogadro’s Law. It tells us that for a gas at constant temperature and pressure, the volume is directly proportional to the number of moles. It’s important to remember that the temperatures in this equation must be in absolute units (Kelvin), not Celsius or Fahrenheit.
This derivation shows that if you have two containers with the same temperature and pressure, the one with more gas molecules will have a larger volume. It’s a fundamental concept that helps us understand how gases will expand or contract when the amount of gas changes.
Imagine you have two containers of equal size. One contains oxygen and the other contains hydrogen. If both containers are at the same temperature and pressure, Avogadro’s Law tells us they contain the same number of molecules, even though the gases are different. Avogadro’s Law is crucial for understanding how gases behave and for calculations involving gas reactions in chemistry. It’s also the foundation for the Ideal Gas Law, which combines Boyle’s Law, Charles’s Law, and Avogadro’s Law into one equation.
Avogadro’s Law simplifies the study of gases by letting us know that under the same conditions, all gases behave similarly in terms of volume and number of particles. It’s a key concept that helps bridge the gap between the microscopic world of molecules and the macroscopic world we can measure.
Combining the Laws
To combine these three laws into one, we take into account that volume is simultaneously proportional to the number of moles and temperature, and inversely proportional to the pressure. Combining these gives us:
\(\displaystyle V \propto \frac{nT}{P} \)
To convert the proportionality into an equation, we introduce a proportionality constant, which is the ideal gas constant (R). This gives us the Ideal Gas Equation:
\(\displaystyle\begin{equation}\label{eqn:4}\boxed{\boldsymbol{ PV = nRT}} \end{equation}\)
The ideal gas constant (R) is a universal constant that relates the energy scale to the temperature scale. It ensures that the units on both sides of the equation match and makes the equation applicable to all ideal gases. The equation of state for an ideal gas is simply the Ideal Gas Equation itself, which relates the macroscopic properties of an ideal gas in a simple form.
Other Forms of the Ideal Gas Equation
Density-Based Equation of the Ideal Gas Equation
The density-based form of the Ideal Gas Equation is a variation that allows us to calculate the pressure of a gas when we know its density and temperature. It’s written as
\(\displaystyle\begin{equation}\label{eqn:5}\boxed{\boldsymbol{ P=\frac{{\rho RT}}{M}}} \end{equation}\)
- P is Pressure: How much force the gas exerts on its container.
- ρ (rho) is Density: The mass of the gas per unit volume.
- R is the Ideal Gas Constant: A number that ensures the units in the equation match up.
- T is Temperature: How hot or cold the gas is, measured in Kelvin.
- M is Molar Mass: The mass of one mole of the gas particles.
Let’s say we have a sample of carbon dioxide (CO₂) at room temperature (about 298 K). We want to find out the pressure exerted by this gas if we know its density and molar mass.
- The molar mass of CO₂ is about 44.01 g/mol.
- Let’s assume the density of our gas sample is 1.977 g/L.
Using the density-based Ideal Gas Equation, we can calculate the pressure:
\(\displaystyle P = \frac{\rho \times R \times T}{M} \)
Plugging in the values, we get:
\(\displaystyle P = \frac{1.977 \text{ g/L} \times 0.0821 \text{ L atm/mol K} \times 298 \text{ K}}{44.01 \text{ g/mol}} \)
After calculating, we would find the pressure in the atmosphere. This equation is particularly useful in scenarios where we can measure the density of a gas directly and want to relate it to pressure and temperature. This form of the equation is great for real-world applications like calculating the pressure of the Earth’s atmosphere at different altitudes, where the density of air changes with height.
Boltzmann’s Constant-Based Equation
This form of the Ideal Gas Equation uses Boltzmann’s constant (k) to relate the energy of individual gas particles to the temperature of the gas. It’s written as
\(\displaystyle\begin{equation}\label{eqn:6}\boxed{\boldsymbol{PV=NkT }} \end{equation}\)
- P is Pressure: The force that gas particles exert on the container walls.
- V is Volume: The space that the gas occupies.
- N is the number of gas particles.
- k is Boltzmann’s Constant: A number that connects the microscopic world of atoms and molecules to the macroscopic properties we can measure.
- T is Temperature: How hot or cold the gas is, measured in Kelvin.
Let’s say we have a sealed box with a fixed number of nitrogen molecules at room temperature (about 298 K). We want to find out the pressure inside the box.
- The number of nitrogen molecules (N) in the box is, let’s say, 10²³.
- Boltzmann’s constant (k) is approximately 1.38 x 10⁻²³ J/K.
- The volume (V) of the box is 0.1 m³.
Using the Boltzmann’s Constant-Based Equation, we can calculate the pressure:
\(\displaystyle P = \frac{N \times k \times T}{V} \)
Plugging in the values, we get:
\(\displaystyle P = \frac{10^{23} \times 1.38 \times 10^{-23} \text{ J/K} \times 298 \text{ K}}{0.1 \text{ m}^3} \)
After calculating, we would find the pressure in Pascals. This equation is particularly useful in scenarios where we’re considering the behavior of gases on a molecular level, such as in the study of kinetic theory or when dealing with very low pressures or high temperatures.
This form of the Ideal Gas Equation is great for connecting the dots between the tiny, fast-moving particles that make up gases and the larger-scale properties like pressure and temperature that we can feel and measure. It helps students understand how the microscopic and macroscopic worlds are linked through physics.
These different forms of the Ideal Gas Equation are like different lenses for a camera. Each one gives you a unique view of the gas, depending on what information you have and what you want to find out. They all come from the same basic understanding of how gases behave, but they let you focus on different aspects, like density or particle energy.
Also Read: Zeroth Law of Thermodynamics
Difference Between Ideal Gas and Real Gas
Ideal gas is a simplified model where the gas particles are tiny points that don’t interact with each other. They bounce around freely, and their behavior is predictable using the Ideal Gas Law: (PV = nRT), where (P) is pressure, (V) is volume, (n) is the number of moles, (R) is the gas constant, and (T) is temperature.
Real gases, however, are a bit more complicated. They have forces between them, and they take up space. These factors make their behavior a bit different from the ideal model, especially when they’re squeezed together (high pressure) or when they’re really cold.
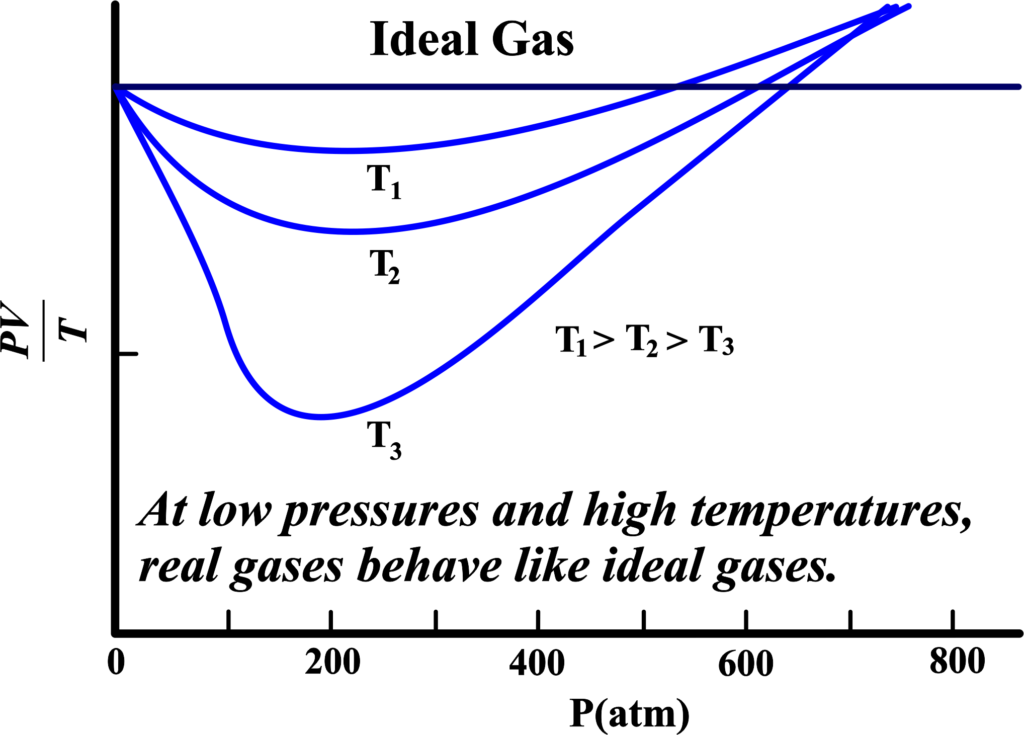
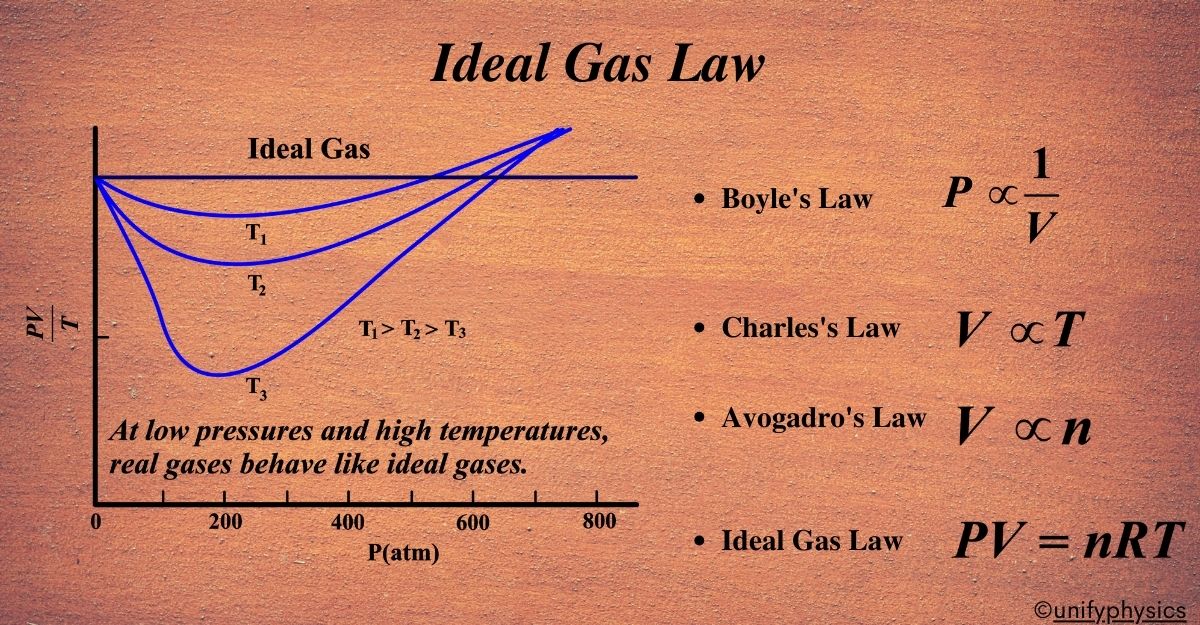
- At High Pressures: The lines on the graph will start to veer off from the ideal behavior. This is because the gas particles are being pushed together, and they start to interact more, which makes them not follow the Ideal Gas Law perfectly.
- At Low Pressures: Here, the lines on the graph will get closer to the ideal line. This is because the gas particles have more space, so they don’t bump into each other as much, and they start to behave more like the ideal gas we talked about.
- At High Temperatures: The gas particles move faster and have more energy. This means they can overcome their attraction to each other, and again, they start acting more like the ideal gas.
So, when we say that “all gases behave like an ideal gas” at low pressures and high temperatures, we’re saying that under these conditions, the real-life complications of gas particles don’t matter as much. The gas acts as if it’s made of those tiny, non-interacting points, just like in our ideal model.
Ideal Gas Vs. Real Gas
Ideal gases are hypothetical and do not have intermolecular forces, while real gases have intermolecular forces and do not always follow the Ideal Gas Law. Real gases deviate from ideal behavior at high pressures and low temperatures. Let’s see the key differences between ideal and real gases.
| Property | Ideal Gas | Real Gas |
|---|---|---|
| Volume | Particles are point masses with no volume. | Particles have significant volume. |
| Intermolecular Forces | No intermolecular forces are present. | Intermolecular forces exist, especially under high pressure and low temperature. |
| Collision Type | Particles have perfectly elastic collisions. | Collisions can be inelastic, especially under high pressure. |
| Existence | Hypothetical, does not exist in reality. | Exists in reality and can be observed. |
| Behavior | Always follows the ideal gas law (PV=nRT) under all conditions. | Follows the ideal gas law only at low pressure and high temperature. Deviates under other conditions. |
| Pressure | Pressure is solely due to collisions with container walls. | Real pressure is lower than ideal due to intermolecular attraction. |
| Compressibility | Not applicable as volume of particles is negligible. | Compressible due to the finite volume of particles. |
| Temperature Effect | No effect on intermolecular forces as they are non-existent. | Low temperatures can lead to liquefaction due to increased intermolecular forces. |
This table summarizes the key differences between ideal and real gases. Ideal gases are a simplified model used in equations and calculations, while real gases are what we find in the natural world, with behaviors that can vary depending on conditions like pressure and temperature.
Solved Examples
Problem 1: Calculate the pressure exerted by 2 moles of an ideal gas in a 10 L container at 300 K. (The universal gas constant (R) is 8.314 J/mol·K).
Solution: The ideal gas law is given by:
\(\displaystyle PV = nRT \)
Given:
- (n = 2 mol)
- (\(\displaystyle V = 10 \, \text{L} = 10 \times 10^{-3} \, \text{m}^3 \))
- (T = 300 K)
- (\(\displaystyle R = 8.314 \, \text{J/mol·K} \))
Substituting the values:
\(\displaystyle P \times 10 \times 10^{-3} = 2 \times 8.314 \times 300 \)
\(\displaystyle P \times 0.01 = 4988.4 \)
\(\displaystyle P = \frac{4988.4}{0.01}\)
P = 498840 Pa
The pressure exerted by 2 moles of an ideal gas in a 10 L container at 300 K is 498840 Pa.
Problem 2: Calculate the density of nitrogen gas (N2) at 2 atm pressure and 273 K. (The molar mass of nitrogen (N2) is 28 g/mol and the universal gas constant (R) is 0.0821 L·atm/mol·K).
Solution: The density (ρ) of a gas is given by:
\(\displaystyle \rho = \frac{PM}{RT} \)
Given:
- (P = 2 atm)
- (T = 273 K)
- (R = 0.0821 L·atm/mol·K)
- (M = 28 g/mol = 0.028 kg/mol)
Substituting the values:
\(\displaystyle \rho = \frac{2 \times 0.028}{0.0821 \times 273} \)
\(\displaystyle \rho = \frac{0.056}{22.4133} \)
\(\displaystyle \rho \approx 0.0025 \, \text{kg/L} \)
The density of nitrogen gas at 2 atm pressure and 273 K is approximately 0.0025 kg/L.
Problem 3: Calculate the average kinetic energy of argon atoms at 400 K. (Boltzmann constant (kB) is (\(\displaystyle 1.38 \times 10^{-23} \, \text{J/K} \)).
Solution: The average kinetic energy (\(\displaystyle\overline{E_k}\)) of a gas molecule is given by:
\(\displaystyle \overline{E_k} = \frac{3}{2} k_B T \)
Given:
- (T = 400 K)
- (\(\displaystyle k_B = 1.38 \times 10^{-23} \, \text{J/K} \))
Substituting the values:
\(\displaystyle \overline{E_k} = \frac{3}{2} \times 1.38 \times 10^{-23} \times 400 \)
\(\displaystyle \overline{E_k} = 3 \times 1.38 \times 10^{-23} \times 200\)
\(\displaystyle \overline{E_k} = 8.28 \times 10^{-21} \)
The average kinetic energy of argon atoms at 400 K is (\(\displaystyle 8.28 \times 10^{-21} \, \text{J} \)).
Problem 4: Calculate the number of molecules in 2 moles of an ideal gas. (Avogadro’s number (NA) is (\(\displaystyle 6.022 \times 10^{23} \, \text{mol}^{-1} \)).
Solution: The number of molecules (N) is given by:
\(\displaystyle N = n \times N_A \)
Given:
- (n = 2 mol)
- (\(\displaystyle N_A = 6.022 \times 10^{23} \, \text{mol}^{-1} \))
Substituting the values:
\(\displaystyle N = 2 \times 6.022 \times 10^{23} \)
\(\displaystyle N = 1.2044 \times 10^{24} \)
The number of molecules in 2 moles of an ideal gas is (\(\displaystyle 1.2044 \times 10^{24} \)).
Problem 5: Calculate the temperature at which 3 moles of an ideal gas occupy a volume of 30 L at 1 atm pressure. (The universal gas constant ( R ) is 0.0821 L·atm/mol·K).
Solution: The ideal gas law is given by:
PV = nRT
Given:
- (P = 1 atm)
- (V = 30 L)
- (n = 3 mol)
- (R = 0.0821 L·atm/mol·K )
Rearranging to solve for (T):
\(\displaystyle T = \frac{PV}{nR} \)
Substituting the values:
\(\displaystyle T = \frac{1 \times 30}{3 \times 0.0821} \)
\(\displaystyle T = \frac{30}{0.2463} \)
\(\displaystyle T \approx 121.8 \, \text{K} \)
The temperature at which 3 moles of an ideal gas occupy a volume of 30 L at 1 atm pressure is approximately 121.8 K.
Problem 6: Calculate the work done by an ideal gas when it expands from 10 L to 20 L at a constant pressure of 2 atm. (1 atm = 101.3 J/L)
Solution: The work done (W) by an ideal gas during an isobaric process is given by:
\(\displaystyle W = P \Delta V \)
Given:
- (P = 2 atm)
- (\(\displaystyle \Delta V = 20 \, \text{L} – 10 \, \text{L} = 10 \, \text{L} \))
- (1 atm = 101.3 J/L)
Substituting the values:
\(\displaystyle W = 2 \times 10 \times 101.3 \)
W = 2026 J
The work done by an ideal gas when it expands from 10 L to 20 L at a constant pressure of 2 atm is 2026 J.
FAQs
What is the Ideal Gas Law, and how does it describe the behavior of gases?
Answer: The Ideal Gas Law is a fundamental equation in thermodynamics that describes the behavior of ideal gases under various conditions. It is expressed as (PV = nRT), where (P) is the pressure of the gas, (V) is its volume, ( n ) is the number of moles of gas, (R) is the gas constant, and (T) is the temperature in Kelvin. This equation relates the pressure, volume, temperature, and amount of gas in a system.
Can you explain when the Ideal Gas Law applies and its limitations?
Answer: The Ideal Gas Law applies to ideal gases, which are hypothetical gases that perfectly follow the law under all conditions. It is most accurate at low pressures and high temperatures, where intermolecular forces are negligible. However, real gases deviate from ideal behavior at high pressures and low temperatures due to interactions between gas molecules.
How does the Ideal Gas Law account for changes in temperature, pressure, and volume of a gas?
Answer: The Ideal Gas Law shows that the product of pressure and volume (PV) is directly proportional to the product of the number of moles of gas and the absolute temperature (nRT). This means that as temperature increases, pressure and volume increase proportionally, while keeping the number of moles constant.
Can the Ideal Gas Law be used to determine the molar mass of a gas?
Answer: Yes, the Ideal Gas Law can be rearranged to solve for the molar mass of a gas. By measuring the pressure, volume, and temperature of a gas sample and knowing the number of moles, one can rearrange the equation to solve for the molar mass (M) using the formula: \(\displaystyle M = \frac{mRT}{PV} \), where (m) is the mass of the gas.
How does the Ideal Gas Law contribute to the understanding of gas behavior in various applications?
Answer: The Ideal Gas Law is used in numerous applications, including in the design of gas storage systems, such as scuba diving tanks and compressed air cylinders. It also helps in understanding the behavior of gases in chemical reactions, gas mixtures, and industrial processes like refrigeration and air conditioning.
What are the units of the gas constant (R) in the Ideal Gas Law?
Answer: The units of the gas constant depend on the units used for pressure, volume, temperature, and the number of moles. In SI units, the gas constant (R) has a value of approximately (8.314) joules per mole-kelvin (J/mol·K). In other unit systems, such as the atmosphere-liter-mole-kelvin (atm·L/mol·K) system, the value of (R) is different.
How does the Ideal Gas Law relate to the kinetic theory of gases?
Answer: The Ideal Gas Law is consistent with the assumptions of the kinetic theory of gases, which describes gases as collections of particles (atoms or molecules) in constant random motion. According to this theory, gas particles have negligible volume and do not interact with each other, which aligns with the behavior described by the Ideal Gas Law.