The Kinetic Theory of Gases is a fundamental concept in physics that describes the behavior of gases at the molecular level. The history of this theory is quite rich and dates back to ancient times, but it was not until the 17th and 19th centuries that significant advancements were made.
The idea that matter is made up of tiny, indivisible particles has its roots in ancient philosophy. Around 50 BCE, the Roman philosopher Lucretius proposed that macroscopic bodies were composed of rapidly moving atoms bouncing off each other. This atomistic view was inspired by earlier Greek philosophers like Democritus and Epicurus.
In 1738, Daniel Bernoulli published “Hydrodynamics,” which laid the groundwork for the kinetic theory. Bernoulli suggested that gases consist of many molecules moving in all directions and that their impact on a surface causes gas pressure. He also connected the average kinetic energy of these molecules with the temperature of the gas.
Despite Bernoulli’s groundbreaking work, the theory wasn’t widely accepted initially, partly because the concept of energy conservation wasn’t established, and the idea of perfectly elastic collisions between molecules was hard to grasp.
It wasn’t until the 19th century that scientists like James Clerk Maxwell and Ludwig Boltzmann made significant contributions to the theory. They developed mathematical models that described the properties of gases, such as pressure and temperature, in terms of molecular motion. These models helped establish many principal concepts of thermodynamics.
Maxwell introduced the idea of the distribution of molecular speeds, which explained why not all gas molecules move at the same speed. Boltzmann further developed statistical mechanics, which provided a deeper understanding of the probabilities associated with molecular speeds and energies.
Today, the kinetic theory of gases is a cornerstone of statistical mechanics and thermodynamics. It helps us understand not just the behavior of gases, but also phenomena like diffusion, viscosity, and heat conductivity.
What is the Kinetic Theory of Gases?
The Kinetic Theory of Gases is like a story that explains what happens in the world of tiny gas particles that are too small to see. Imagine a gas as a crowd of super tiny, invisible balls (these are the molecules) all moving around super fast in all directions. These balls are constantly bouncing off each other and the walls of their container, like in a game of bumper cars. Now, let’s say you have a balloon filled with air. According to the Kinetic Theory:
- The air inside the balloon is made up of a bunch of these tiny balls (molecules).
- These balls are always moving around randomly and super fast.
- They don’t care about each other, meaning they don’t stick together or push each other away—they just bounce off when they collide.
- The size of these balls is small compared to the space they have in the balloon.
- When these balls hit the wall of the balloon, they push on it a little bit. This push is what we feel as pressure.
- The temperature of the gas is a measure of how fast these balls are moving. If we heat the balloon, the balls move faster, and the balloon gets bigger because the pressure increases.
So, in simple terms, the Kinetic Theory of Gases tells us that gases are made up of many small particles moving in random directions, and their movement explains properties like pressure and temperature. It’s a way to connect the dots between the tiny, invisible world of molecules and the big things we can feel and measure, like the air in our balloons.
Kinetic Theory of Gases Assumptions
The Kinetic Theory of Gases provides a framework for understanding how gas molecules behave. Here are the assumptions with scientific examples:
- Molecules are in Constant Motion: Imagine a balloon filled with helium gas. The reason the balloon stays inflated is that the helium molecules are constantly moving and colliding with the inner walls of the balloon, exerting pressure.
- Molecules are Far Apart: In a gas like hydrogen at room temperature and atmospheric pressure, the molecules are spaced far apart relative to their size. This is why gases are compressible, unlike solids or liquids.
- Collisions are Elastic: When two billiard balls collide, they bounce off each other without losing kinetic energy. Similarly, gas molecules bounce off each other and the container walls without any energy loss.
- No Forces Except During Collisions: Gas molecules don’t attract or repel each other except during collisions. This is like astronauts floating in the International Space Station; they don’t come together or move apart unless they push off something.
- Obey Laws of Motion: All gas molecules, regardless of their size, obey Newton’s laws of motion. This is evident in how different gases mix evenly and completely in a room, as their molecules move and spread out according to these laws.
- Steady State is Reached: When you spray perfume in a room, the fragrance molecules spread out and eventually reach a steady state where their concentration becomes uniform throughout the room.
- Uniform Density: The atmosphere around Earth is a mixture of different gases. Despite the movement and mixing of these gases, the atmosphere maintains a uniform density at a given altitude.
These assumptions help us predict and calculate the behavior of gases under various conditions, such as changes in pressure, volume, and temperature, using mathematical models.
Postulates of Kinetic Theory of Gases
The Kinetic Theory of Gases gives us a set of rules that describe how gas particles behave. These rules, or postulates, help us understand why gases act the way they do.
- Tiny, Busy Particles: The first postulate tells us that gas is made up of a huge number of tiny particles, which could be atoms or molecules, and they are always moving around in random directions. It’s like a crowd of people all walking around a huge room, each going their way.
- Negligible Size: These particles are so small that if we compare the size of one particle to the space it moves in, the particle’s size is almost nothing. This is why we can squeeze a gas into a smaller space, and it will just spread out to fill whatever space it’s given.
- No Cliques or Fights: The particles don’t attract or repel each other under normal conditions. They are like strangers in a large hall, not interacting with each other unless they accidentally bump into one another.
- Bouncy Collisions: When these particles hit each other or the walls of their container, they bounce off without losing any energy. It’s like having super bouncy balls that never stop bouncing.
- Energy and Temperature: The average energy of all these moving particles is directly related to the temperature of the gas. So, if the temperature goes up, the particles move faster because they have more energy.
These postulates form the foundation of the Kinetic Theory and help explain the behavior of gases, such as pressure and temperature changes. They are crucial for understanding how gases will react under different conditions, which is important for many scientific and industrial processes.
Also Read: Ideal Gas Law
The Pressure of an Ideal Gas
The pressure exerted by a gas is due to the collisions of the molecules with the walls of the container. According to the theory, pressure is proportional to the number of collisions and the force of each collision.
Imagine you have a balloon filled with air. The air inside is made up of lots of tiny particles called molecules. These molecules are always moving around super fast and bouncing off each other and the walls of the balloon. Now, every time these molecules hit the walls of the balloon, they push on it just a tiny bit. This push from all the molecules hitting the walls creates what we call pressure.
Now, let’s talk about an ideal gas. An ideal gas is a simplified model that scientists use to describe how gases behave under certain conditions. For an ideal gas, we assume a few things:
- The gas particles are so small that we can ignore their size.
- The particles don’t attract or repel each other; they just bounce off when they collide.
- The collisions between the particles and the walls of the container are perfectly elastic, meaning they don’t lose energy when they bounce.
So, the pressure of an ideal gas comes from all these tiny, invisible particles hitting the walls of their container. The harder they hit and the more often they hit, the higher the pressure.
In physics, we have a cool equation called the Ideal Gas Law that connects pressure (P), volume (V), temperature (T), and the number of particles (n) in a gas. It looks like this:
\(\displaystyle P \times V = n \times R \times T \)
Here, (R) is a constant called the universal gas constant. This equation tells us that if we know any three of these things (pressure, volume, temperature, and number of particles), we can figure out the fourth.
For example, if we heat up the balloon, the molecules move faster, hit the walls harder, and more often, so the pressure goes up. If we squeeze the balloon to make it smaller (decrease the volume), the molecules have less room to move, so they hit the walls more often, and again, the pressure goes up.
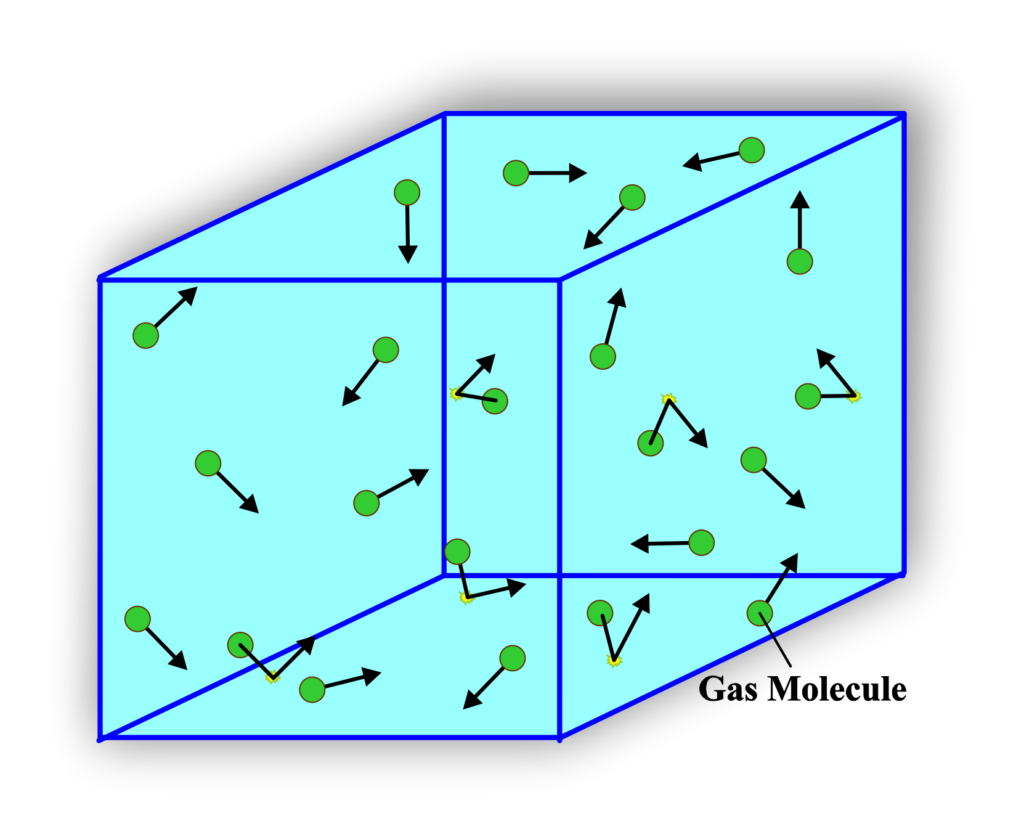
Imagine a cubic container with a volume (V) that holds (N) molecules of an ideal gas. Each molecule has a mass (m). The molecules are moving in random directions with various velocities. We’ll focus on the x-component of the velocity, (vx), for molecules hitting the walls perpendicular to the x-axis.
When a molecule collides with the wall, it rebounds elastically, reversing its x-component of velocity and thus changing its momentum by (2mvx). The time it takes for a molecule to travel across the container and back is
\(\displaystyle\frac{2L}{v_x} \)
where (L) is the length of the container. The force exerted by one molecule on the wall is the rate of change of momentum, which is
\(\displaystyle\frac{2mv_x^2}{2L} = \frac{mv_x^2}{L} \)
Summing up the forces exerted by all molecules on the wall and dividing by the area (L2) gives the pressure (P) exerted by the gas. The mean kinetic energy of the molecules is related to the temperature (T) of the gas by
\(\displaystyle \frac{1}{2}mv_x^2 = \frac{3}{2}kT \)
Combining all these factors, we arrive at the equation for pressure:
\(\displaystyle\begin{equation}\label{eqn:1}\boxed{\boldsymbol{P = \frac{1}{3}\rho \overline{v^2} }} \end{equation}\)
Here, \(\displaystyle\rho\) is the density of the gas, and \(\displaystyle\overline{v^2} \) is the mean square speed of the molecules. This derivation shows that the pressure of an ideal gas is directly proportional to the density and the mean square speed of its molecules, and it also connects the macroscopic properties of the gas to the microscopic motion of its molecules.
Kinetic Interpretation of Temperature
The kinetic interpretation of temperature is based on the idea that the temperature of a substance is directly related to the average kinetic energy of its particles. In simpler terms, temperature measures how much energy the particles of a substance have due to their motion.
- Particles in Motion: Whether in solids, liquids, or gases, particles are always moving. In solids, they vibrate in place; in liquids, they slide past each other; and in gases, they move freely in all directions.
- Temperature and Energy: The faster these particles move, the more kinetic energy they have, and the higher the temperature of the substance.
- Absolute Zero: The lowest possible temperature, called absolute zero (-273.15°C or 0 Kelvin), is theoretically the point at which particles have minimal motion and kinetic energy.
Consider a balloon filled with helium gas. As the temperature of the gas increases, the helium atoms move faster, increasing the balloon’s internal pressure. This is because the kinetic energy of the atoms, and thus the temperature, is higher.
The average kinetic energy (KEavg) of a particle is related to the temperature (T) by the equation:
\(\displaystyle\begin{equation}\label{eqn:2}\boxed{\boldsymbol{ KE_{avg} = \frac{3}{2}kT}} \end{equation}\)
where (k) is the Boltzmann constant. This equation shows that the average kinetic energy is proportional to the absolute temperature of the gas.
Various Speeds of Gas Molecules
Gas molecules move at different speeds, and we can describe these using:
Root Mean Square Speed (RMS)
The RMS speed is a statistical measure that gives us an idea of the average speed of gas molecules in a sample. It’s particularly useful because it relates directly to the kinetic energy of the molecules, which is a fundamental concept in thermodynamics.
In any gas, molecules are constantly moving in random directions with a variety of speeds. To find the RMS speed, we square each molecule’s speed, take the average of these squares, and then take the square root of that average. This process eliminates any negative values that could arise from squaring and gives us a single speed value that represents the entire gas.
\(\displaystyle v_{rms} = \sqrt{\frac{1}{N}\sum_{i=1}^{N}v_i^2} \)
where (vrms) is the RMS speed, (N) is the number of molecules, and (vi ) is the speed of each molecule. Consider a container of helium gas at room temperature. The RMS speed of the helium atoms can be calculated using the formula:
\(\displaystyle\begin{equation}\label{eqn:3}\boxed{\boldsymbol{ v_{rms} = \sqrt{\frac{3kT}{m}} }} \end{equation}\)
where (k) is the Boltzmann constant, (T) is the absolute temperature, and (m) is the mass of a helium atom.
For instance, at 298 K (room temperature), the RMS speed of helium atoms can be calculated by plugging in the values for (k), (T), and the molar mass of helium converted to the mass of a single atom. This gives us a specific value in meters per second, which represents the average speed of the helium atoms in the container. By understanding RMS speed, students can better grasp concepts like diffusion and reaction rates, which depend on the speed of the molecules involved.
Most Probable Speed
The Most Probable Speed is the speed at which the largest number of molecules in a gas sample is moving. It’s a specific value that comes from the Maxwell-Boltzmann distribution, which is a statistical distribution of the speeds of molecules in a gas.
In a gas, molecules are constantly moving around at different speeds. If we could see them, we’d notice that some are moving slowly, some are moving quickly, and many are somewhere in between. The speeds of these molecules form a bell-shaped curve when plotted on a graph. This curve shows us that a few molecules are moving very slowly or very quickly, but most are moving at a speed somewhere in the middle. The peak of this bell-shaped curve represents the Most Probable Speed. It’s not the average or the fastest speed, but the speed that which most molecules are moving.
Let’s say we have a container of oxygen gas at room temperature. The Most Probable Speed of the oxygen molecules can be calculated using the formula:
\(\displaystyle\begin{equation}\label{eqn:4}\boxed{\boldsymbol{v_{mp} = \sqrt{\frac{2kT}{m}} }} \end{equation}\)
where (vmp) is the Most Probable Speed, and (m) is the mass of an oxygen molecule.
For example, at 298 K (room temperature), we can plug in the values for (k), (T), and the mass of an oxygen molecule to find the Most Probable Speed. This gives us a specific value in meters per second, which tells us the speed at which the majority of oxygen molecules are moving inside the container. Understanding the Most Probable Speed helps students grasp how temperature affects the movement of molecules and is crucial for predicting how gases will behave under different conditions.
Average Speed of Gas Molecules
The Average Speed is the arithmetic mean of the speeds of all the molecules in a gas. It’s different from the Most Probable Speed (which most molecules have) and the Root Mean Square Speed (which is related to the average kinetic energy).
Gas molecules are in constant, random motion, colliding with each other and the walls of their container. To find the Average Speed, we add up the speeds of all the molecules and divide by the number of molecules. This gives us a single speed that represents the overall motion of the gas.
\(\displaystyle\begin{equation}\label{eqn:5}\boxed{\boldsymbol{v_{avg} = \sqrt{\frac{8kT}{\pi m}} }} \end{equation}\)
where \(\displaystyle v_{avg} \) is the Average Speed,(m) is the mass of a single molecule, and \(\displaystyle \pi \) is the mathematical constant Pi.
Let’s consider a sample of nitrogen gas at room temperature. Using the formula above, we can calculate the Average Speed of the nitrogen molecules by substituting the values for (k), (T), and the mass of a nitrogen molecule. This calculation will give us a value in meters per second, which represents the average speed at which the nitrogen molecules are moving within the sample. Understanding the Average Speed of gas molecules is important for predicting how gases will behave under various conditions, such as diffusion rates and reaction kinetics.
Maxwell-Boltzmann Distribution
This distribution describes the spread of energies and speeds among the molecules in a gas. It shows that at any given temperature, there is a variety of speeds and energies, with most molecules having speeds close to the most probable speed.
Imagine you’re at a huge concert with thousands of people. Everyone is moving to the music, but not everyone is dancing at the same speed. Some are jumping around energetically, some are swaying gently, and others are just tapping their feet. Now, if we wanted to create a chart showing how many people are dancing at different speeds, we’d end up with a graph that shows the Maxwell-Boltzmann Distribution for the concert.
In a gas, molecules are like the people at the concert, moving at different speeds. Some move fast, some slow, and many at an average pace. The Maxwell-Boltzmann Distribution is a graph that shows us how the speeds of these molecules are spread out. It’s a curve that tells us how likely we are to find a molecule moving at a certain speed. Just like the energy of the music affects how people dance, the temperature of the gas affects how fast the molecules move. If we heat the gas, the peak of the graph shifts to the right, meaning more molecules are moving faster.
The distribution is described by a mathematical equation that looks a bit complex, but it essentially tells us the probability of finding a molecule at a certain speed based on the temperature and the mass of the molecules:
\(\displaystyle f(v) = \left(\frac{m}{2\pi kT}\right)^{\frac{3}{2}} 4\pi v^2 e^{-\frac{mv^2}{2kT}} \)
where f(v) is the probability density function for speed (v), (m) is the mass of a molecule. This distribution is super important in real life. For example, it helps us understand how different gases will react with each other, which is crucial for things like predicting the weather or designing engines.
So, the Maxwell-Boltzmann Distribution gives us a way to visualize and calculate how molecules in a gas move around at different temperatures.
Solved Examples
Problem 1: Calculate the root mean square (rms) speed of oxygen molecules at 300 K. (The molar mass of oxygen (O2) is 32 g/mol and the universal gas constant (R) is 8.314 J/mol·K).
Solution: The rms speed (vrms) is given by:
\(\displaystyle v_{\text{rms}} = \sqrt{\frac{3RT}{M}} \)
First, convert the molar mass (M) to kg/mol:
\(\displaystyle M = 32 \, \text{g/mol} = 0.032 \, \text{kg/mol} \)
Given:
- (T = 300 K)
- (R = 8.314 J/mol·K)
Substituting the values:
\(\displaystyle v_{\text{rms}} = \sqrt{\frac{3 \times 8.314 \times 300}{0.032}} \)
\(\displaystyle v_{\text{rms}} = \sqrt{\frac{7482.6}{0.032}} \)
\(\displaystyle v_{\text{rms}} = \sqrt{233206.25} \)
\(\displaystyle v_{\text{rms}} \approx 483 \, \text{m/s} \)
The rms speed of oxygen molecules at 300 K is approximately 483 m/s.
Problem 2: Calculate the mean free path (λ) of nitrogen molecules in a gas at standard temperature and pressure (STP). The diameter of a nitrogen molecule is (\(\displaystyle 3 \times 10^{-10} \, \text{m} \)) and the number density (n) at STP is (\(\displaystyle 2.7 \times 10^{25} \, \text{m}^{-3} \)).
Solution: The mean free path (λ) is given by:
\(\displaystyle \lambda = \frac{1}{\sqrt{2} \pi d^2 n} \)
Given:
- (\(\displaystyle d = 3 \times 10^{-10} \, \text{m} \))
- (\(\displaystyle n = 2.7 \times 10^{25} \, \text{m}^{-3}\))
Substituting the values:
\(\displaystyle \lambda = \frac{1}{\sqrt{2} \pi (3 \times 10^{-10})^2 (2.7 \times 10^{25})} \)
\(\displaystyle \lambda = \frac{1}{\sqrt{2} \pi (9 \times 10^{-20}) (2.7 \times 10^{25})} \)
\(\displaystyle \lambda = \frac{1}{\sqrt{2} \pi \times 2.43 \times 10^{6}} \)
\(\displaystyle \lambda = \frac{1}{3.421 \times 10^{6}} \)
\(\displaystyle \lambda \approx 2.92 \times 10^{-7} \, \text{m} \)
The mean free path of nitrogen molecules at STP is approximately (\(\displaystyle 2.92 \times 10^{-7} \, \text{m}\) ).
Problem 3: Calculate the average kinetic energy of helium molecules at 400 K. (Boltzmann constant (kB) is (\(\displaystyle 1.38 \times 10^{-23} \, \text{J/K} )\)).
Solution: The average kinetic energy (\(\displaystyle\overline{E_k} \)) of a gas molecule is given by:
\(\displaystyle \overline{E_k} = \frac{3}{2} k_B T \)
Given:
- (T = 400 K)
- (\(\displaystyle k_B = 1.38 \times 10^{-23} \, \text{J/K} \))
Substituting the values:
\(\displaystyle \overline{E_k} = \frac{3}{2} \times 1.38 \times 10^{-23} \times 400 \)
\(\displaystyle \overline{E_k} = 3 \times 1.38 \times 10^{-23} \times 200 \)
\(\displaystyle \overline{E_k} = 8.28 \times 10^{-21} \)
The average kinetic energy of helium molecules at 400 K is (\(\displaystyle 8.28 \times 10^{-21} \, \text{J}\)).
Problem 4: Calculate the pressure exerted by 1 mole of an ideal gas in a 22.4 L container at 273 K.
Solution: The ideal gas law is given by:
PV = nRT
Given:
- (n = 1 mol)
- (\(\displaystyle V = 22.4 \, \text{L} = 22.4 \times 10^{-3} \, \text{m}^3 \))
- (T = 273 K)
- (R = 8.314 J/mol·K)
Substituting the values:
\(\displaystyle P \times 22.4 \times 10^{-3} = 1 \times 8.314 \times 273 \)
\(\displaystyle P = \frac{8.314 \times 273}{22.4 \times 10^{-3}} \)
\(\displaystyle P = \frac{2269.422}{0.0224} \)
\(\displaystyle P = 101325 \, \text{Pa} \)
The pressure exerted by 1 mole of an ideal gas in a 22.4 L container at 273 K is 101325 Pa.
Problem 5: Calculate the ratio of specific heat (γ) for a diatomic gas.
Solution: For a diatomic gas:
\(\displaystyle C_V = \frac{5}{2} R \)
\(\displaystyle C_P = \frac{7}{2} R \)
The ratio of specific heats (γ) is given by:
\(\displaystyle \gamma = \frac{C_P}{C_V} \)
Substituting the values:
\(\displaystyle \gamma = \frac{\frac{7}{2} R}{\frac{5}{2} R} \)
\(\displaystyle \gamma = \frac{7}{5} \)
\(\displaystyle \gamma = 1.4 \)
The ratio of specific heats (γ) for a diatomic gas is 1.4.
Problem 6: If the most probable speed of nitrogen molecules at 300 K is 422 m/s, calculate the mass of a nitrogen molecule. (Boltzmann constant (kB) is (\(\displaystyle 1.38 \times 10^{-23} \, \text{J/K} \)).
Solution: The most probable speed (vp) is given by:
\(\displaystyle v_p = \sqrt{\frac{2k_BT}{m}} \)
Rearrange to solve for (m):
\(\displaystyle m = \frac{2k_BT}{v_p^2} \)
Given:
- (vp = 422 m/s)
- (T = 300 K)
- (\(\displaystyle k_B = 1.38 \times 10^{-23} \, \text{J/K} \))
Substituting the values:
\(\displaystyle m = \frac{2 \times 1.38 \times 10^{-23} \times 300}{422^2} \)
\(\displaystyle m = \frac{8.28 \times 10^{-21}}{178084} \)
\(\displaystyle m \approx 4.65 \times 10^{-26} \, \text{kg} \)
The mass of a nitrogen molecule is approximately (\(\displaystyle 4.65 \times 10^{-26} \, \text{kg}\) ).
FAQs
What is the Kinetic Theory of Gases, and how does it explain the behavior of gases?
The Kinetic Theory of Gases is a model that describes gases as collections of tiny particles (atoms or molecules) in constant, random motion. It explains gas behavior by relating the macroscopic properties of gases, such as pressure, volume, and temperature, to the microscopic behavior of their constituent particles.
Can you explain how the Kinetic Theory of Gases accounts for gas pressure?
According to the Kinetic Theory, gas pressure arises from the collisions of gas particles with the walls of their container. As gas particles move randomly and collide with each other and the container walls, they exert a force on the walls, resulting in pressure.
What is the Maxwell-Boltzmann distribution, and why is it important?
The Maxwell-Boltzmann distribution is a statistical distribution that describes the range of speeds (or energies) of molecules in a gas. It’s important because it provides a way to calculate the likelihood of finding a molecule at a certain speed and is fundamental to understanding gas behavior at the molecular level.
How does the Kinetic Theory of Gases explain the relationship between temperature and the average kinetic energy of gas particles?
The Kinetic Theory states that the temperature of a gas is proportional to the average kinetic energy of its particles. As temperature increases, the average kinetic energy of gas particles also increases, leading to faster motion and more frequent collisions.
How does the Kinetic Theory of Gases explain the diffusion and effusion of gases?
According to the Kinetic Theory, gas molecules move randomly and independently of each other. Diffusion occurs when gas molecules spread out and mix with other gases due to their random motion. Effusion, on the other hand, is the process by which gas molecules escape through a small opening into a vacuum, also due to their random motion.
What are the main assumptions of the Kinetic Theory of Gases?
The main assumptions are:
- Gas molecules are in constant, random motion.
- The volume of individual molecules is negligible compared to the container’s volume.
- Collisions between molecules are perfectly elastic.
- There are no intermolecular forces except during collisions.
Can the Kinetic Theory of Gases explain deviations from ideal gas behavior?
Yes, the Kinetic Theory can explain deviations from ideal gas behavior observed at high pressures and low temperatures. These deviations occur because gas particles may interact with each other (resulting in attractive or repulsive forces) or occupy significant volumes compared to the volume of the container, violating the assumptions of the ideal gas model.
Can the Kinetic Theory of Gases be applied to liquids and solids?
While the Kinetic Theory is primarily used to describe gases, some principles can be extended to liquids and solids. However, because the intermolecular forces in liquids and solids are much stronger than in gases, the theory requires modifications to accurately describe these states of matter.
How does the Kinetic Theory of Gases relate to real-world phenomena and applications?
The Kinetic Theory of Gases provides a fundamental understanding of gas behavior, which is crucial in various scientific and technological fields. It is used in the design of engines, refrigeration systems, and air conditioning units, as well as in understanding atmospheric phenomena like weather patterns and the behavior of pollutants in the atmosphere.