The concept of energy distribution among particles has been a topic of curiosity and research for centuries. However, it was in the 19th century that significant progress was made in understanding this phenomenon. The groundwork for the Law of Equipartition of Energy was laid by the kinetic theory of gases, which describes how the motion of particles in a gas leads to its macroscopic properties like pressure and temperature.
Pioneering scientists like James Clerk Maxwell and Ludwig Boltzmann played crucial roles in the development of this law. They used statistical mechanics, a branch of physics that deals with large numbers of particles and their collective behavior, to predict how energy is shared among particles.
Maxwell introduced the idea that the velocities of particles in a gas follow a particular distribution, now known as the Maxwell-Boltzmann distribution. This was a stepping stone to understanding how energy is distributed among particles. Boltzmann extended these ideas and introduced concepts like degrees of freedom—different ways in which a particle can store energy. He proposed that at thermal equilibrium, each degree of freedom would have the same average energy.
The culmination of these efforts led to the formulation of the equipartition theorem, which states that energy is equally partitioned among all available degrees of freedom in a system at thermal equilibrium. This law became a fundamental principle in thermodynamics and statistical mechanics, providing a deeper understanding of the internal energy of systems and influencing the development of modern physics.
What is the Law of Equipartition of Energy?
The Law of Equipartition of Energy is a fascinating concept from the world of thermodynamics and statistical mechanics. It’s like a rule for energy equality among particles in a system. Imagine you’re at a party, and there’s a cake to share. Everyone gets an equal slice of the cake, right? Similarly, the Law of Equipartition of Energy says that when particles are jiggling around in a system, like atoms in a gas, they share their energy equally among all the different ways they can move.
Degrees of Freedom: These “ways to move” are called degrees of freedom. For example, a particle can move left or right, up or down, forward or backward. These are three degrees of freedom because there are three different directions it can go. If it can also rotate or vibrate, those are more degrees of freedom.
Energy Sharing: Here’s the cool part: for each degree of freedom, the particle gets a little bit of energy. And if you know the temperature of the system, you can calculate this energy! The formula looks like this:
\(\displaystyle E = \frac{1}{2}kT \)
where (E) is the average energy per degree of freedom, (k) is a constant called the Boltzmann constant, and (T) is the temperature in Kelvin.
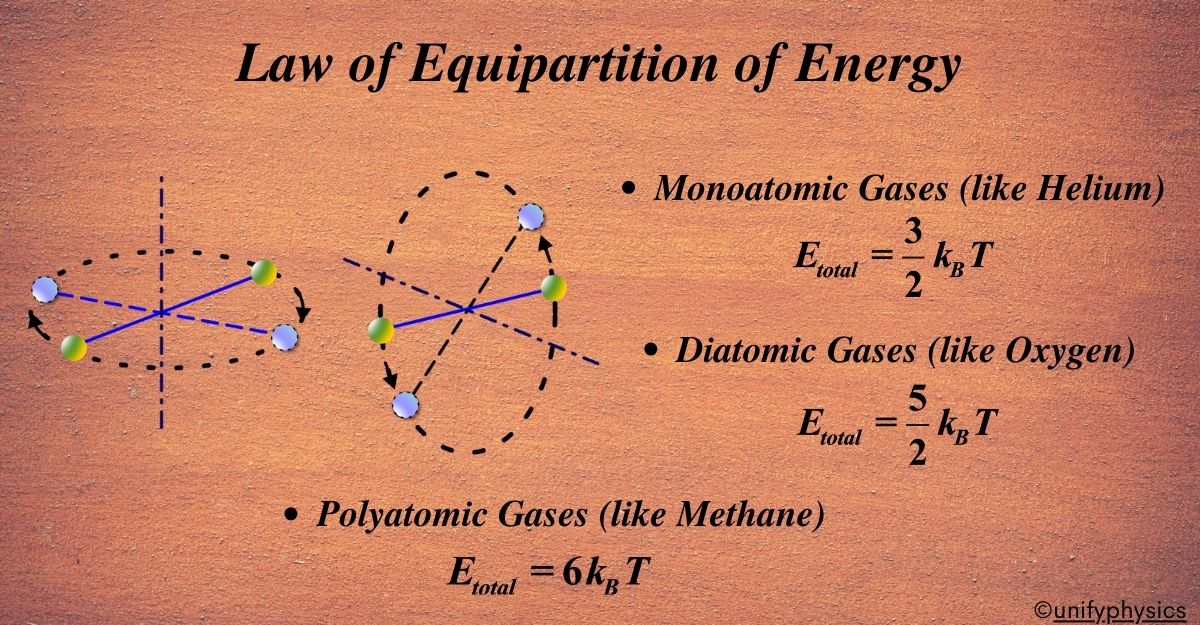
- Monoatomic Gases (like Helium): These simple atoms can only move in space, so they have 3 degrees of freedom. According to the law, each degree gets \(\displaystyle\frac{1}{2}kT \) energy, so the total energy is \(\displaystyle\frac{3}{2}kT \).
- Diatomic Gases (like Oxygen): These have 3 degrees of freedom for moving in space and 2 for rotating, making it 5 degrees. So, the total energy is \(\displaystyle\frac{5}{2}kT \).
- Polyatomic Gases (like Methane): These can have even more degrees of freedom because they can move, rotate, and vibrate in complex ways.
Understanding this law helps us predict how gases will behave under different conditions, like changes in temperature or pressure. This understanding also helps us explain why the air in a room is at a certain temperature, or how energy spreads out in a gas. It’s a fundamental principle that shows us how the microscopic movements of particles relate to the everyday temperatures we feel.
In summary, the Law of Equipartition of Energy tells us that energy is shared equally among all the possible movements (degrees of freedom) of particles in a system at a constant temperature.
Monoatomic Gases: A Study of Helium and Its Kinetic Energy
Monoatomic gases are the simplest kind of gases. They consist of single atoms, not bonded to any others. Helium is a perfect example of a monoatomic gas. In a helium gas, each atom is independent and doesn’t form molecules with other helium atoms. This simplicity makes their behavior easier to predict and understand.
Degrees of Freedom: In physics, when we talk about degrees of freedom, we’re referring to the different ways an object can move. For monoatomic gases, each atom can move in three ways:
- Along the x-axis (left or right)
- Along the y-axis (up or down)
- Along the z-axis (forward or backward)
These are called translational degrees of freedom because they involve translating or moving, from one place to another. Kinetic energy is the energy that an object has because of its motion. According to the Law of Equipartition of Energy, each degree of freedom contributes an equal amount of energy to the total kinetic energy of the atom. For monoatomic gases, this energy is given by the formula: \(\displaystyle E = \frac{1}{2}kTE\) .Since a monoatomic gas like helium has three degrees of freedom, the total kinetic energy per atom is:
\(\displaystyle E_{total} = 3 \times \frac{1}{2}kT\)
\(\displaystyle E_{total} = \frac{3}{2}kT \)
In a Nutshell, Monoatomic gases are like single atoms on a playground. They can run in any direction—forward, backward, left, right, up, or down. And when it comes to energy, they get an equal share for each way they can move. That’s why understanding them is a breeze—they’re as straightforward as gases get!
Diatomic Gases: An Insight into Oxygen and Its Kinetic Energy
Diatomic gases are like the dynamic duos of the gas world. “Di” means two, and “atomic” means atoms, so diatomic gases are made up of molecules with two atoms each. These two atoms are bonded together like best friends holding hands.
Oxygen is one of the most well-known diatomic gases. It’s essential for life on Earth because we breathe it in to help our bodies produce energy. In the air, oxygen exists as O2, which means two oxygen atoms are joined together.
Degrees of Freedom: Unlike monoatomic gases, diatomic gases have more degrees of freedom.
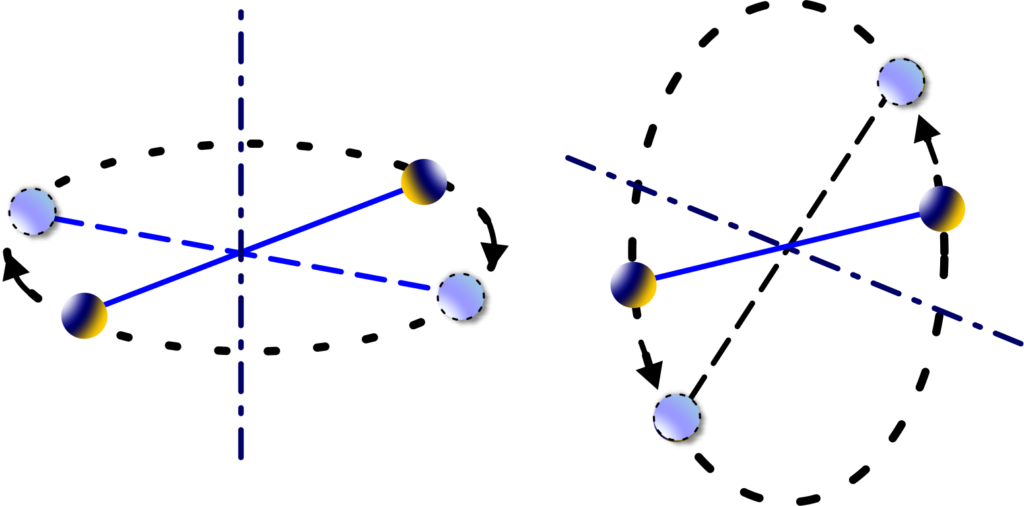
They can move in three dimensions, just like monoatomic gases, but they can also rotate. Imagine a pair of dancers spinning around—they can turn from side to end over end. That’s like the rotational movement of diatomic molecules.
The kinetic energy in diatomic gases is shared among these degrees of freedom. According to the Law of Equipartition of Energy, each degree of freedom gets an average energy of \(\displaystyle\frac{1}{2}kT \).
For diatomic gases like oxygen, the total kinetic energy per molecule can be calculated by adding the energy from all degrees of freedom:
\(\displaystyle E_{total} = E_{translational} + E_{rotational}\)
\(\displaystyle E_{total} = \frac{3}{2}kT + \frac{2}{2}kT\)
\(\displaystyle E_{total} = \frac{5}{2}kT \)
In simpler terms, if you think of an oxygen molecule as a tiny barbell floating in space, it can move up or down, left or right, forward or backward, and it can also spin around. For each of these movements, it has a little bit of energy. When you add up all that energy for each movement, you get the total kinetic energy for the molecule.
Polyatomic Gases and Their Kinetic Energy: Methane as an Example
Polyatomic gases, such as methane, are composed of molecules with more than two atoms. These gases are fascinating due to their complex structure and unique ways of interacting with light and other forms of energy, making them important in studies of the atmosphere and climate change.
Methane: A Simple Polyatomic Gas
Methane (CH₄), a common example of a polyatomic gas, consists of one carbon atom at the center and four hydrogen atoms at the corners, akin to a soccer ball and its players on the field.
Degrees of Freedom: The Ways They Move
Polyatomic gases like methane have more degrees of freedom than monoatomic or diatomic gases. They can move, rotate, and even vibrate. Each bond between atoms can stretch and bend, adding to the molecule’s degrees of freedom. Specifically,
- Translational degrees of freedom: Moving in three dimensions (x, y, z).
- Rotational degrees of freedom: Spinning around their axes.
- Vibrational degrees of freedom: Atoms within the molecule move relative to each other.
Energy Distribution in Polyatomic Gases
The energy in polyatomic gases is shared among all these degrees of freedom. For translational and rotational movements, each degree of freedom gets an average energy of \(\displaystyle\frac{1}{2}kT \). Vibrational modes are a bit different. Each vibrational mode counts as two degrees of freedom—one for the kinetic energy of the vibration and one for the potential energy. So, for each vibrational mode, the molecule gets (kT) of energy.
For a methane molecule, we have:
- 3 translational degrees of freedom: \(\displaystyle\frac{3}{2}kT \) of energy.
- 3 rotational degrees of freedom: \(\displaystyle\frac{3}{2}kT \) of energy.
- Vibrational degrees of freedom: Depending on the number of vibrational modes, each contributing (kT) of energy.
If methane had, say, 3 vibrational modes (which is not the actual number for methane), the total kinetic energy would be calculated by adding the energy from all degrees of freedom:
\(\displaystyle E_{total} = E_{translational} + E_{rotational} + E_{vibrational} \)
\(\displaystyle E_{total} = \frac{3}{2}kT + \frac{3}{2}kT + 3kT \)
\(\displaystyle E_{total} = 6kT \)
In polyatomic gases like methane, the kinetic energy per molecule is the sum of the energy in all the degrees of freedom. Remember, the actual number of vibrational modes will vary based on the specific molecule’s structure. This makes polyatomic gases a bit more complex than their monoatomic and diatomic cousins, but it also makes them essential in the study of physics and chemistry as they show us how energy is stored and transferred in more complex systems.
Also Read: Ideal Gas Law
Significance of Equipartition of Energy
This law helps us understand the internal energy of gases and contributes to the calculation of specific heat, predicting values that agree well with experiments for monoatomic gases.
- Understanding Thermal Energy: This law helps us understand what thermal energy is. We know that temperature is a measure of how hot or cold something is, but what’s happening on the inside? Well, it’s all about how the tiny particles (like atoms and molecules) are moving. The Law of Equipartition of Energy tells us that these particles share their energy equally among all the ways they can move or vibrate.
- Predicting Gas Behavior: It’s super useful in predicting how gases will behave. For example, if you heat a gas, you’re giving energy to its particles. This law helps us predict how that energy will spread out among the particles and what that means for things like pressure and volume.
- Calculating Specific Heats: The law is crucial for calculating the specific heats of substances. Specific heat is a number that tells us how much energy is needed to change the temperature of a substance. Because the law tells us how energy is divided up, we can use it to figure out specific heat for different materials.
- Bridging Micro and Macro Worlds: It bridges the gap between the microscopic world of atoms and the macroscopic world we experience. By understanding how energy is distributed among particles, we can explain why a metal rod gets hot evenly when heated or why the air in a room has a uniform temperature.
- Real-World Applications: This law has real-world applications in engineering and technology. For instance, it helps engineers design better engines and refrigerators by understanding how energy is distributed in the gases they use.
Limitations of Equipartition of Energy
The Law of Equipartition of Energy is super helpful, but it’s not perfect. There are some situations where it doesn’t quite work as expected. Here’s why:
- Low Temperatures: At very low temperatures, the law starts to break down. It predicts that energy should still be spread out evenly among all degrees of freedom, but in reality, some types of motion, like vibrations, freeze out. This means they stop contributing to the energy distribution, which the law doesn’t account for.
- Quantum Effects: The law is based on classical physics, which works great for everyday situations. But when you get down to the level of atoms and subatomic particles, quantum mechanics takes over. Quantum effects can lead to energy being distributed in ways that the Law of Equipartition of Energy doesn’t predict.
- High-Frequency Vibrations: For molecules that vibrate at very high frequencies, the law doesn’t always hold up. That’s because these vibrations can have quantized energy levels, meaning they can only take on certain values. The law assumes that energy can be of any value and spread out smoothly, which isn’t the case here.
- Non-Ergodic Systems: In some complex systems, energy doesn’t flow freely between all degrees of freedom. These are called non-ergodic systems. The law assumes that energy can move around and be shared equally, but if it gets stuck or doesn’t mix well, the law won’t apply.
- Interactions Between Particles: The law works best for ideal gases, where particles don’t interact with each other. But in real life, particles do interact, and these interactions can affect how energy is distributed. The law doesn’t take these interactions into account.
Solved Examples
Problem 1: Calculate the internal energy of 2 moles of a monoatomic ideal gas at a temperature of (300 K).
Solution: For a monoatomic gas, each atom has 3 degrees of freedom (translational). According to the law of equipartition of energy, the energy per degree of freedom is:
\(\displaystyle \frac{1}{2} k_B T \)
Thus, the total energy per molecule is:
\(\displaystyle \epsilon = \frac{3}{2} k_B T \)
For 1 mole of gas:
\(\displaystyle U = \frac{3}{2} N_A k_B T = \frac{3}{2} RT \)
For (n) moles of gas:
\(\displaystyle U = n \cdot \frac{3}{2} RT \)
Given:
- (n = 2)
- (R = 8.314 J/mol·K)
- (T = 300 K)
\(\displaystyle U = 2 \times \frac{3}{2} \times 8.314 \times 300 \)
\(\displaystyle U = 3 \times 8.314 \times 300 \)
\(\displaystyle U = 24.942 \times 300 \)
\(\displaystyle U \approx 7482.6 \, \text{J} \)
The internal energy of 2 moles of a monoatomic ideal gas at (300 K) is approximately (7482.6 J).
Problem 2: Calculate the internal energy of 1 mole of a diatomic ideal gas at a temperature of (400 K).
Solution: For a diatomic gas, each molecule has 5 degrees of freedom (3 translational and 2 rotational) at room temperature. The energy per degree of freedom is:
\(\displaystyle \frac{1}{2} k_B T \)
Thus, the total energy per molecule is:
\(\displaystyle \epsilon = \frac{5}{2} k_B T \)
For 1 mole of gas:
\(\displaystyle U = \frac{5}{2} N_A k_B T = \frac{5}{2} RT \)
Given:
- (n = 1)
- (R = 8.314 J/mol·K)
- (T = 400 K)
\(\displaystyle U = 1 \times \frac{5}{2} \times 8.314 \times 400 \)
\(\displaystyle U = 2.5 \times 8.314 \times 400 \)
\(\displaystyle U = 20.785 \times 400 \)
\(\displaystyle U \approx 8314 \, \text{J} \)
The internal energy of 1 mole of a diatomic ideal gas at (400 K) is approximately (8314 J).
Problem 3: Calculate the specific heat capacity at constant volume (CV) for a monoatomic ideal gas.
Solution: For a monoatomic gas:
\(\displaystyle U = \frac{3}{2} nRT \)
The molar specific heat capacity at constant volume (CV) is:
\(\displaystyle C_V = \left( \frac{\partial U}{\partial T} \right)_V \)
Since:
\(\displaystyle U = \frac{3}{2} nRT \)
\(\displaystyle C_V = \frac{3}{2} nR \)
For 1 mole:
\(\displaystyle C_V = \frac{3}{2} R \)
Given:R = 8.314 J/mol·K)
\(\displaystyle C_V = \frac{3}{2} \times 8.314 \)
\(\displaystyle C_V = 12.471 \, \text{J/mol·K} \)
The specific heat capacity at constant volume for a monoatomic ideal gas is (12.471 J/mol·K).
Problem 4: Calculate the internal energy of 3 moles of a linear triatomic ideal gas at (350 K).
Solution: For a linear triatomic gas, each molecule has 7 degrees of freedom (3 translational, 2 rotational, and 2 vibrational). At moderate temperatures, vibrational modes may not be fully excited, so we consider 5 active degrees of freedom.
Total energy per molecule is:
\(\displaystyle \epsilon = \frac{7}{2} k_B T \)
For 1 mole of gas:
\(\displaystyle U = \frac{7}{2} N_A k_B T = \frac{7}{2} RT \)
For (n) moles of gas:
\(\displaystyle U = n \cdot \frac{7}{2} RT \)
Given:
- (n = 3)
- (R = 8.314 J/mol·K)
- (T = 350 K)
\(\displaystyle U = 3 \times \frac{7}{2} \times 8.314 \times 350 \)
\(\displaystyle U = \frac{21}{2} \times 8.314 \times 350 \)
\(\displaystyle U = 10.5 \times 8.314 \times 350 \)
\(\displaystyle U = 2911.2 \times 350 \)
\(\displaystyle U \approx 1010000 \, \text{J} \)
The internal energy of 3 moles of a linear triatomic ideal gas at (350 K) is approximately ( 1010000 J).
Problem 5: Calculate the ratio of specific heat capacities ( \(\displaystyle\gamma = \frac{C_P}{C_V} \)) for a diatomic ideal gas.
Solution: For a diatomic gas:
\(\displaystyle C_V = \frac{5}{2} R \)
\(\displaystyle C_P = C_V + R \)
So,
\(\displaystyle C_P = \frac{5}{2} R + R = \frac{7}{2} R \)
The ratio (γ) is:
\(\displaystyle \gamma = \frac{C_P}{C_V} = \frac{\frac{7}{2} R}{\frac{5}{2} R} = \frac{7}{5} = 1.4 \)
The ratio of specific heat capacities (γ) for a diatomic ideal gas is ( 1.4 ).
Problem 6: Calculate the average translational kinetic energy of a single molecule of an ideal gas at a temperature of (500 K).
Solution: The average translational kinetic energy per molecule is given by:
\(\displaystyle \langle E_{\text{trans}} \rangle = \frac{3}{2} k_B T \)
Given:
- (\(\displaystyle k_B = 1.38 \times 10^{-23} \, \text{J/K}\) )
- (T = 500 K)
\(\displaystyle \langle E_{\text{trans}} \rangle = \frac{3}{2} \times 1.38 \times 10^{-23} \times 500 \)
\(\displaystyle \langle E_{\text{trans}} \rangle = \frac{3}{2} \times 6.9 \times 10^{-21} \)
\(\displaystyle \langle E_{\text{trans}} \rangle = 10.35 \times 10^{-21} \)
\(\displaystyle \langle E_{\text{trans}} \rangle = 1.035 \times 10^{-20} \, \text{J} \)
The average translational kinetic energy of a single molecule of an ideal gas at (500 K) is (\(\displaystyle 1.035 \times 10^{-20} \, \text{J} \)).
FAQs
How does the Law of Equipartition of Energy relate to the kinetic theory of gases?
In the kinetic theory of gases, the Law of Equipartition of Energy explains how energy is distributed among the translational, rotational, and vibrational degrees of freedom of gas molecules. It predicts that, on average, each degree of freedom contributes \(\displaystyle\frac{1}{2}kT \) to the total energy of a molecule.
Can you explain how the Law of Equipartition of Energy applies to different types of molecules?
The Law of Equipartition of Energy applies to all molecules with multiple degrees of freedom, including linear molecules (with three translational and two rotational degrees of freedom), nonlinear molecules (with three translational and three rotational degrees of freedom), and molecules with vibrational modes.
What happens when a system deviates from thermal equilibrium regarding the Law of Equipartition of Energy?
Deviations from thermal equilibrium can lead to unequal energy distributions among different degrees of freedom. For example, if certain degrees of freedom are restricted or inhibited (e.g., due to molecular interactions or quantum effects), the Law of Equipartition of Energy may no longer hold, and energy distribution may become non-uniform.
How does the Law of Equipartition of Energy contribute to our understanding of heat capacity?
The Law of Equipartition of Energy helps explain the relationship between the heat capacity of a system and its degrees of freedom. For a monoatomic ideal gas, each atom has three translational degrees of freedom, resulting in a molar heat capacity of \(\displaystyle \frac{3}{2}R \), where ( R ) is the gas constant.
Can the Law of Equipartition of Energy be applied to systems beyond gases?
Yes, the Law of Equipartition of Energy can be applied to various systems beyond gases, including solids and liquids. In solids, energy is distributed among vibrational modes of atoms or molecules, while in liquids, energy distribution involves both translational and rotational motion of molecules.
How does quantum mechanics challenge the classical interpretation of the Law of Equipartition of Energy?
Quantum mechanics introduces the concept of quantized energy levels, which can lead to deviations from the classical Law of Equipartition of Energy at low temperatures or for systems with restricted degrees of freedom. Quantum effects, such as zero-point energy, can result in non-classical energy distributions that do not follow the predictions of classical thermodynamics.
Why doesn’t the ‘Law of Equipartition of Energy’ hold true at very low temperatures?
At very low temperatures, quantum effects become significant, and the classical assumption that energy can be any value and is spread out smoothly doesn’t hold. Some degrees of freedom, like vibrations, may not be activated, and the energy isn’t distributed as the law predicts.
Audio
Summary of the Law of Equipartition of Energy