The concept of the mean free path has its roots in the kinetic theory of gases, which was developed in the 19th century. This theory was a major step forward in understanding how gases behave at the molecular level.
The kinetic theory describes the motion of particles in a gas and how they interact with each other. Early scientists like James Clerk Maxwell and Ludwig Boltzmann contributed significantly to this theory. They introduced the idea that gas particles are in constant, random motion and that this motion is related to the temperature of the gas.
Maxwell was one of the first to describe the distribution of velocities among the molecules in a gas, now known as the Maxwell-Boltzmann distribution. He also discussed how often molecules in a gas would collide, leading to the concept of the mean free path.
Boltzmann further developed these ideas and is known for the Boltzmann equation, which describes the behavior of a particle in a fluid or gas. His work helped to explain how properties like pressure and temperature arise from the collective behavior of many particles.
The term ‘mean free path’ emerged from these studies to quantify the average distance a particle travels before colliding with another particle. It was a crucial concept because it linked the microscopic behavior of individual particles with the macroscopic properties of the gas as a whole.
Today, the mean free path is important in understanding gases and fields like semiconductor physics and even astronomy. It helps scientists predict how particles will behave in different conditions, which is essential for designing new materials and technologies.
Free Path
The ‘free path’ is the distance a particle, like a molecule or atom, travels before it collides with another particle. Imagine you’re playing a game of tag in a field with your friends. The field is filled with obstacles, and you’re trying to avoid being tagged. The free path is like the distance you can run without touching any obstacles. In physics, when we talk about gases, the obstacles are other gas molecules, and the runner is a single gas molecule.
- A free path is the straight-line distance a gas molecule travels before it bumps into another molecule.
- Just like in the game, some paths are short (you run into someone right away), and some are long (you manage to dodge everyone for a while).
- The lengths of these paths vary a lot because the molecules are moving randomly.
By understanding the free path, we can predict how gases will behave, like how they’ll spread out in a room or how they’ll react under pressure.
You could demonstrate this by having students walk around randomly in a space, noting how far they get before they have to change direction due to an obstacle (another student). This hands-on activity helps visualize the concept and shows that while each path is different, there’s an average distance that can be calculated. The concept of free path is not just for understanding gases. It’s also used in fields like electronics, where it describes how far electrons can move in a material before they’re scattered.
What is the Mean Free Path?
The ‘mean free path’ is the average distance a particle travels between collisions. It’s like averaging out the distances you walked in the crowded room before each bump. The Mean Free Path (MFP) is a term used in physics to describe the average distance a particle, such as a molecule in a gas, travels before it collides with another particle. It’s a statistical measure that gives us an idea of how ‘free’ a particle is to move without interruption.
Let’s consider a real-world example involving a beam of light passing through the atmosphere. Photons, which are particles of light, have their mean free path when they travel through air. The MFP of photons in the atmosphere is determined by the number of air molecules and other particles that can scatter or absorb the light.
When sunlight enters the Earth’s atmosphere, it interacts with molecules and particles in the air. The blue sky we see is actually due to the scattering of sunlight by the atmosphere. Blue light scatters more than other colors because it travels as shorter, smaller waves. This is known as Rayleigh scattering.
In this case, the mean free path of the blue photons is shorter than that of red photons, which is why the sky appears blue during the day. At sunrise and sunset, the sun’s light has to pass through more of the Earth’s atmosphere, which increases the mean free path for blue light to the point where it’s scattered out of the line of sight, and the red and orange hues dominate.
How do we Measure the Mean Free Path?
Measuring the mean free path involves looking at many particles over time and calculating the average distance they travel between collisions.
Measuring the MFP of particles in a gas involves understanding their random motion and interactions. Since we can’t track every single molecule, scientists use statistical methods to estimate the MFP. The MFP, denoted by (λ), is the average distance a molecule travels between collisions. It’s calculated using the formula:
\(\displaystyle\lambda = \frac{1}{\sqrt{2} \pi d^2 N/V}\)
where (d) is the diameter of a molecule, (N) is the number of molecules, and (V) is the volume of the gas.
In the field of radiography, the MFP is used to describe the average distance a photon travels before interacting with atoms in the target material. This interaction depends on the material’s composition and the energy of the photons. For instance, in medical imaging, understanding the MFP of X-rays in human tissue helps in adjusting the dosage and quality of the image.
A simple classroom activity to demonstrate the concept of MFP could involve using a large container filled with small, uniformly sized balls to represent molecules. By shaking the container and allowing one ball to move freely, students can observe how it collides with others. By marking its path and measuring the distances between collisions, students can calculate an average distance, which represents the MFP.
Mean Free Path Factors
When we talk about the mean free path of particles, like molecules in a gas, we’re referring to the average distance they travel before colliding with another molecule. Several factors can affect this distance:
- The density of the Gas: Think of a room full of people. If the room is crowded, you can’t walk far without bumping into someone. Similarly, in a dense gas with many molecules close together, collisions happen more often, and the mean free path is shorter.
- Number of Molecules: This is like the number of people in the room. More people mean you’re more likely to collide with someone, just as more molecules in a gas increase the chances of collisions, reducing the mean free path.
- Size of the Molecules: If everyone in the room is carrying large backpacks, you’ll bump into others more often. In the same way, larger molecules in a gas will collide more frequently, which decreases the mean free path.
- Temperature: If people in the room start moving faster, maybe because there’s a sale in the next room, they’ll bump into each other more often. Higher temperatures make gas molecules move faster, leading to more collisions and a shorter mean-free path.
- Pressure: Higher pressure is like squeezing more people into the room. It pushes the molecules closer together, increasing the likelihood of collisions and decreasing the mean free path.
Also Read: Kinetic Theory of Gases
Formula of Mean Free Path
The mean free path (MFP) is the average distance a particle, like a gas molecule, travels before it collides with another molecule. The formula for MFP is given by:
\(\displaystyle\lambda = \frac{1}{\sqrt{2} \pi d^2 N/V}\)
- (λ ): This is the mean free path itself.
- (d): The diameter of a molecule. It’s like measuring how wide a ball is.
- (N): The total number of molecules in the gas.
- (V): The volume the gas occupies. Think of it as the size of a room filled with air.
The formula tells us that the mean free path is inversely related to the number of molecules and their size. More molecules or bigger molecules mean a shorter mean free path because collisions will be more frequent.
The \(\displaystyle\sqrt{2} \) and \(\displaystyle\pi \) are there because of the geometry involved in the motion and collisions of the molecules.
Imagine you have a bunch of marbles in a box. If the marbles are small and there aren’t many, they can roll around quite a bit before hitting each other. That’s a long free path. But if the marbles are large or the box is packed with them, they’ll bump into each other a lot more. That’s a short mean free path.
Derivation of the Formula of Mean Free Path
Imagine a gas molecule moving around and bumping into other molecules. We want to find out how far it goes on average before it hits another molecule. Here’s how we can figure that out:
Assumptions:
- All molecules are hard spheres with the same diameter (d).
- The gas molecules are evenly spread out in the space they occupy.
- We focus on one molecule moving while others are stationary.
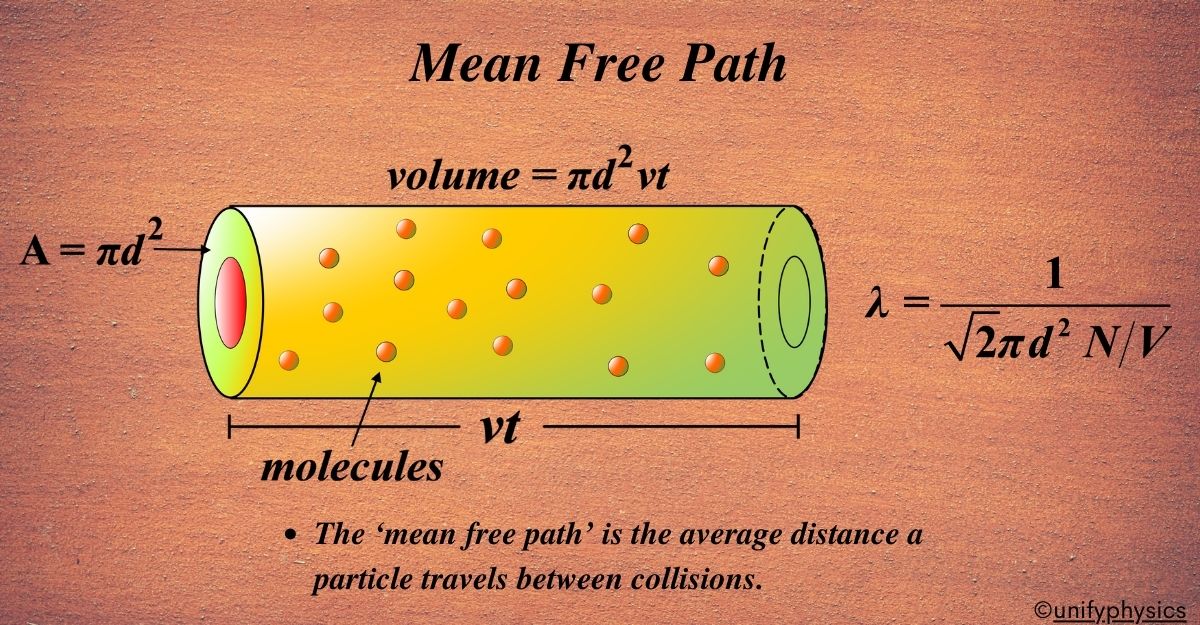
Our moving molecule sweeps out a path like a cylinder as it goes. The volume of this cylinder is the area of the circle (the end of the cylinder) times the length of the cylinder.
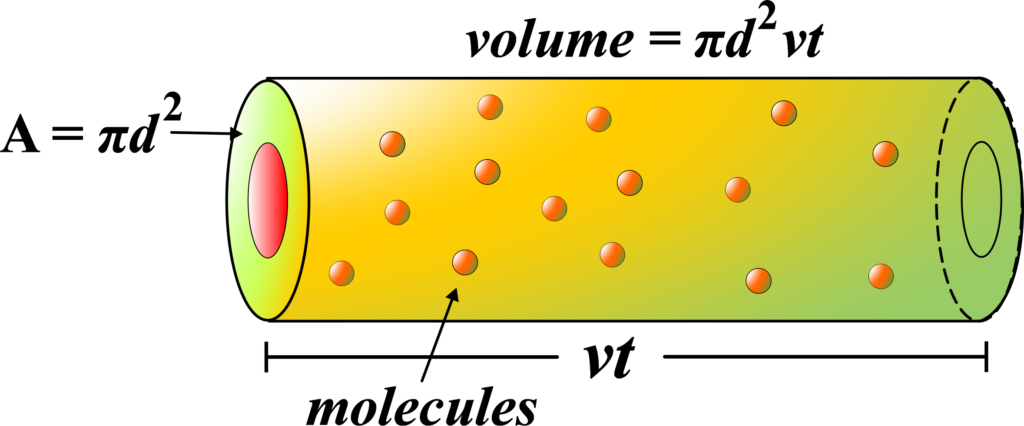
The area of the circle is \(\displaystyle\pi d^2 \) because the radius of the circle is \(\displaystyle\frac{d}{2} \), and the area of a circle is \(\displaystyle\pi r^2 \). The length of the cylinder is the distance the molecule travels, which we’ll call (λ), the MFP we’re trying to find.
If ( N ) is the total number of molecules and (V) is the volume they’re in, then \(\displaystyle\frac{N}{V} \) is the number of molecules per unit volume. The number of collisions our molecule has is the number of molecules in the volume of the cylinder it sweeps out.
- The volume of the cylinder is \(\displaystyle\pi d^2 \times \lambda \).
- The number of collisions is \(\displaystyle\frac{N}{V} \times \pi d^2 \times \lambda \).
- We expect 1 collision in the mean free path, so we set the number of collisions to 1 and solve for λ:
\(\displaystyle\lambda = \frac{1}{\sqrt{2} \pi d^2 \frac{N}{V}}\)
This equation is the mean free path (λ), the average distance a molecule travels before it collides with another molecule. This derivation simplifies the real situation by assuming other molecules are stationary and doesn’t account for their motion, but it gives us a good approximation for the MFP in a gas.
Solved Examples
Problem 1: Calculate the mean free path of oxygen molecules at a temperature of 300 K and a pressure of 1 atm. The diameter of an oxygen molecule is (\(\displaystyle 3 \times 10^{-10} \)) m.
Solution: The mean free path (λ) is given by:
\(\displaystyle \lambda = \frac{k_B T}{\sqrt{2} \pi d^2 P} \)
Given:
- (T = 300 K)
- (\(\displaystyle P = 1 \, \text{atm} = 1.01 \times 10^5 \, \text{Pa} \))
- (\(\displaystyle d = 3 \times 10^{-10} \, \text{m} \))
- (\(\displaystyle k_B = 1.38 \times 10^{-23} \, \text{J/K} \))
\(\displaystyle\lambda = \frac{1.38 \times 10^{-23} \times 300}{\sqrt{2} \pi (3 \times 10^{-10})^2 \times 1.01 \times 10^5} \)
\(\displaystyle \lambda = \frac{4.14 \times 10^{-21}}{3.14 \times 9 \times 10^{-20} \times 1.01 \times 10^5} \)
\(\displaystyle \lambda = \frac{4.14 \times 10^{-21}}{2.86 \times 10^{-14}} \)
\(\displaystyle \lambda \approx 1.45 \times 10^{-7} \, \text{m} \)
The mean free path of oxygen molecules at 300 K and 1 atm is approximately (\(\displaystyle 1.45 \times 10^{-7} \, \text{m}\) ).
Problem 2: If the pressure of the gas in Problem 1 is reduced to 0.5 atm, what is the new mean free path of the oxygen molecules?
Solution: Using the same formula:
\(\displaystyle \lambda = \frac{k_B T}{\sqrt{2} \pi d^2 P} \)
Given:\(\displaystyle P = 0.5 \, \text{atm} = 0.5 \times 1.01 \times 10^5 \, \text{Pa} = 5.05 \times 10^4 \, \text{Pa} \)
\(\displaystyle\lambda = \frac{1.38 \times 10^{-23} \times 300}{\sqrt{2} \pi (3 \times 10^{-10})^2 \times 5.05 \times 10^4} \)
\(\displaystyle \lambda = \frac{4.14 \times 10^{-21}}{3.14 \times 9 \times 10^{-20} \times 5.05 \times 10^4} \)
\(\displaystyle \lambda = \frac{4.14 \times 10^{-21}}{1.43 \times 10^{-14}} \)
\(\displaystyle \lambda \approx 2.90 \times 10^{-7} \, \text{m} \)
The new mean free path of the oxygen molecules at 0.5 atm is approximately (\(\displaystyle 2.90 \times 10^{-7} \, \text{m} \)).
Problem 3: If the temperature of the gas in Problem 1 is increased to 600 K while keeping the pressure constant, what is the new mean free path?
Solution: \(\displaystyle\lambda = \frac{k_B T}{\sqrt{2} \pi d^2 P} \)
Given:
- (T = 600 K)
- ( \(\displaystyle P = 1 \, \text{atm} = 1.01 \times 10^5 \, \text{Pa} \))
\(\displaystyle \lambda = \frac{1.38 \times 10^{-23} \times 600}{\sqrt{2} \pi (3 \times 10^{-10})^2 \times 1.01 \times 10^5} \)
\(\displaystyle \lambda = \frac{8.28 \times 10^{-21}}{2.86 \times 10^{-14}} \)
\(\displaystyle \lambda \approx 2.90 \times 10^{-7} \, \text{m} \)
The mean free path of oxygen molecules at 600 K and 1 atm is approximately (\(\displaystyle 2.90 \times 10^{-7} \, \text{m} \)).
Problem 4: Calculate the mean free path of nitrogen molecules at 300 K and 1 atm. The diameter of a nitrogen molecule is (\(\displaystyle 4 \times 10^{-10} \)) m.
Solution:
\(\displaystyle \lambda = \frac{k_B T}{\sqrt{2} \pi d^2 P} \)
Given:
- (T = 300 K)
- (\(\displaystyle P = 1 \, \text{atm} = 1.01 \times 10^5 \, \text{Pa} \))
- (\(\displaystyle d = 4 \times 10^{-10} \, \text{m}\) )
\(\displaystyle \lambda = \frac{1.38 \times 10^{-23} \times 300}{\sqrt{2} \pi (4 \times 10^{-10})^2 \times 1.01 \times 10^5} \)
\(\displaystyle \lambda = \frac{4.14 \times 10^{-21}}{3.14 \times 16 \times 10^{-20} \times 1.01 \times 10^5} \)
\(\displaystyle \lambda = \frac{4.14 \times 10^{-21}}{5.05 \times 10^{-14}} \)
\(\displaystyle \lambda \approx 8.20 \times 10^{-8} \, \text{m}\)
The mean free path of nitrogen molecules at 300 K and 1 atm is approximately (\(\displaystyle 8.20 \times 10^{-8} \, \text{m} \)).
Problem 5: Given the mean free path of oxygen molecules is (\(\displaystyle 1.45 \times 10^{-7} \)) m at 300 K and 1 atm, find the mean free path of hydrogen molecules under the same conditions, given that the diameter of a hydrogen molecule is (\(\displaystyle 2.8 \times 10^{-10} \)) m.
Solution:
\(\displaystyle \lambda = \frac{k_B T}{\sqrt{2} \pi d^2 P}\)
Given:\(\displaystyle d_{\text{H2}} = 2.8 \times 10^{-10} \, \text{m} \)
\(\displaystyle \lambda_{\text{H2}} = \frac{1.38 \times 10^{-23} \times 300}{\sqrt{2} \pi (2.8 \times 10^{-10})^2 \times 1.01 \times 10^5} \)
\(\displaystyle \lambda_{\text{H2}} = \frac{4.14 \times 10^{-21}}{2.28 \times 10^{-14}} \)
\(\displaystyle \lambda_{\text{H2}} \approx 1.82 \times 10^{-7} \, \text{m} \)
The mean free path of hydrogen molecules at 300 K and 1 atm is approximately (\(\displaystyle 1.82 \times 10^{-7} \, \text{m} \)).
Problem 6: Determine the average time between collisions (mean free time) for nitrogen molecules at 300 K and 1 atm, given the mean free path is (\(\displaystyle 8.20 \times 10^{-8} \)) m and the average speed of nitrogen molecules at this temperature is (470 m/s).
Solution: The mean free time (τ) is given by:
\(\displaystyle \tau = \frac{\lambda}{v_{\text{avg}}} \)
Given:
- (\(\displaystyle \lambda = 8.20 \times 10^{-8} \, \text{m} \))
- (\(\displaystyle v_{\text{avg}} = 470 \, \text{m/s} \))
\(\displaystyle \tau = \frac{8.20 \times 10^{-8}}{470}\)
\(\displaystyle \tau \approx 1.74 \times 10^{-10} \, \text{s} \)
The average time between collisions for nitrogen molecules at 300 K and 1 atm is approximately (\(\displaystyle 1.74 \times 10^{-10} \, \text{s} \)).
FAQs
What is the Mean Free Path, and why is it important in the study of gases?
The Mean Free Path is the average distance traveled by a particle between successive collisions in a gas. It is a crucial parameter in understanding the behavior of gases, as it determines the frequency and nature of collisions between gas particles and their surroundings.
How does the Mean Free Path relate to the density and pressure of a gas?
The Mean Free Path is inversely proportional to the density of the gas and directly proportional to the volume occupied by each gas molecule. As the density of the gas increases, the distance between gas molecules decreases, leading to shorter mean free paths. Similarly, higher pressures result in more frequent collisions and shorter mean free paths.
Can you explain how the Mean Free Path affects the conductivity of gases?
In gases, conductivity is influenced by the Mean Free Path, as it determines the distance over which gas particles can transfer momentum or energy through collisions. Shorter mean free paths result in higher collision frequencies, and increasing conductivity, while longer mean free paths lead to fewer collisions and lower conductivity.
How does the Mean Free Path change with variations in temperature and molecular mass?
The Mean Free Path is directly proportional to temperature and inversely proportional to molecular mass. Increasing the temperature of a gas increases the average speed of gas molecules, resulting in longer mean free paths. Conversely, gases with lighter molecules have longer mean free paths compared to gases with heavier molecules at the same temperature and pressure.
What factors influence the accuracy of the Mean Free Path calculation?
The accuracy of the Mean Free Path calculation depends on factors such as the assumptions made about gas behavior (e.g., ideal gas behavior), the accuracy of experimental measurements (e.g., temperature, pressure), and the consideration of molecular interactions (e.g., van der Waals forces) that may affect collision frequencies.
How does the Mean Free Path relate to the concept of Knudsen flow?
Knudsen flow occurs when the mean free path of gas molecules is comparable to or larger than the characteristic length of the flow channel, leading to non-continuum gas behavior. In such cases, gas molecules exhibit individual particle behavior rather than bulk flow, and the Mean Free Path becomes a critical parameter in determining flow characteristics.
Can you provide real-world examples where knowledge of the Mean Free Path is essential?
Knowledge of the Mean Free Path is crucial in various fields, including gas dynamics, vacuum technology, and semiconductor manufacturing. It is used to design and optimize gas flow systems, such as in vacuum pumps, chemical vapor deposition processes, and microfluidic devices, where gas behavior at the molecular level significantly impacts performance and efficiency.