In the early 20th century, scientists were making huge strides in understanding the quantum world. They discovered that electrons orbit the nucleus in atoms at specific energy levels, much like how planets orbit the sun.
In 1928, a physicist named Felix Bloch took these quantum ideas and applied them to solids. He proposed that electrons in a crystal lattice could be described by a wave function that repeats itself, just like the pattern of atoms in a crystal.
Around the same time, in 1927, two other physicists, Walter Heitler and Fritz London, discovered that when atoms come together, their energy levels begin to merge into ‘bands’. These bands are very closely spaced energy levels that electrons can occupy.
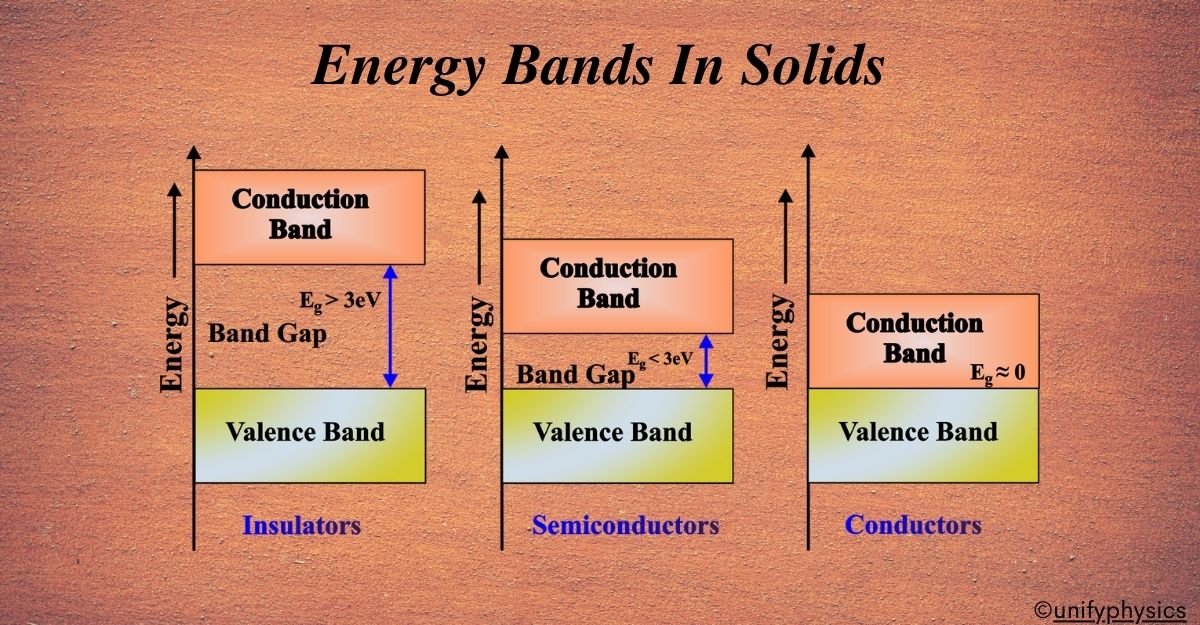
Combining these ideas, scientists developed the Band Theory. They realized that in a solid, the energy levels of electrons are not discrete but form continuous bands. This was a game-changer because it helped explain why some materials conduct electricity well (metals), some don’t at all (insulators), and some are in-between (semiconductors). Today, Band Theory is a cornerstone of solid-state physics. It’s essential for understanding and designing new materials for electronics, from the silicon in your smartphone to the next generation of solar panels.
Formation of Energy Bands
When atoms come close together to form a solid, their energy levels overlap and form energy bands. These bands represent ranges of energy that electrons within the solid can have. Imagine a class full of students, each sitting at their desk, which represents an atom. When the class is empty, each desk (or atom) is separate from the others. This is like atoms in a gas, where each atom’s electrons have their energy levels.
Now, as the classroom fills up and students sit closer to each other, they start to share items like pencils and erasers, which can move from one desk to another. In a solid, this is similar to how electrons start to interact with neighboring atoms.
As the students (or atoms) get even closer, the items being shared (representing the electrons) start to form a common pool in the middle of the group. This pool is like an energy band. It’s no longer just one student’s pencil or eraser; it’s a shared resource that any of the students can use.
In the same way, when many atoms are packed closely together in a solid, their outer energy levels overlap and merge to form bands. These energy bands are ranges of energy that the electrons can have within the solid. Electrons can move freely within these bands, just like the pencils and erasers can be used by any student in the group.
So, the formation of energy bands is all about how individual energy levels of atoms blend when they’re close enough in a solid. This blending allows electrons to move around, which is essential for the electrical properties of materials.
Energy Bands in Solids
(i) Valence Band: The Valence Band is the energy band that consists of valence electrons energy levels, and it’s present below the Conduction Band. The electrons in this band are loosely bound to the nucleus of the atom. This is the energy band that contains the valence electrons. It’s the highest range of electron energies where electrons are still bound to atoms. Think of a solid as a big building with many floors. Each floor represents a different energy level that electrons can occupy. Now, the Valence Band is like the topmost occupied floor where the electrons live.
At absolute zero temperature, this floor is fully occupied by electrons. These electrons are somewhat like the residents of the floor—they have their apartments (atoms) and they don’t usually wander around the building (solid). They’re bound to their atoms and are responsible for holding the atoms together, much like how people in their homes contribute to the stability of the building.
Now, when energy is added (like heating the solid), some of these electrons can get excited and move to higher floors (energy levels). If they gain enough energy, they can even reach the next available floor, which is the Conduction Band. But the Valence Band is their home base.
So, the Valence Band is crucial because it’s the source of electrons for electrical conductivity. If all the apartments on this floor are full, the solid won’t conduct electricity well. But if there’s room for the electrons to move around (like in a metal), the solid will be a good conductor.
(ii) Conduction Band: Electrons here can move freely within the material, contributing to electrical conductivity. Imagine a concert where the Valence Band is on the ground floor where most of the audience is seated. They are enjoying the show but are mostly stationary in their seats. Now, the Conduction Band is like the upper balcony where people can stand up, dance, and move around freely.
In solids, the Conduction Band is the range of energy levels that lies above the Valence Band. Electrons here are like the people on the balcony—they have enough energy to move around freely. This movement is what allows them to carry an electric current through the material.
When an external energy source, like electricity or heat, is applied to a solid, some electrons from the Valence Band can get excited enough to jump up into the Conduction Band. Once there, they’re no longer tied to any particular atom and can move throughout the material, contributing to its electrical conductivity.
The Conduction Band is crucial for understanding how materials conduct electricity. If the Conduction Band is empty, there are no free electrons to carry the current, and the material is an insulator. But if there are electrons in the Conduction Band, the material can conduct electricity and is called a conductor.
When the Conduction Band is partially filled:
When the Conduction Band is partially filled, it means that there are available energy states that electrons can occupy. This partial filling allows for the movement of electrons within the band, which is essential for electrical conductivity.
In metals, for example, the valence band and conduction band often overlap, or the conduction band is partially filled even without external energy. This overlapping or partial filling means that electrons can easily move from the valence band to the conduction band and vice versa. As a result, electrons can flow freely under an applied electric field, which is why metals are such good conductors of electricity.
In semiconductors, the conduction band is not normally filled, but it can become partially filled when energy is added, such as from heat or light. This is what allows semiconductors to conduct electricity under certain conditions. So, the partial filling of the conduction band is a key factor in determining the electrical properties of a material.
As the temperature of a material increases, the energy of the electrons also increases. This added energy allows more electrons to jump from the Valence Band to the Conduction Band. In semiconductors, for instance, the increase in temperature reduces the band gap, making it easier for electrons to be excited into the conduction band.
In metals, the electrons are already present in the conduction band, but as temperature rises, their kinetic energy increases, which can affect their mobility and, consequently, the material’s conductivity.
In summary, an increase in temperature generally leads to an increase in the number of charge carriers (electrons or holes) in the conduction band, which can increase the electrical conductivity of the material. However, it’s important to note that too high a temperature can also lead to increased resistance due to the scattering of electrons.
(iii) Forbidden Band: Also known as the band gap, it’s the energy range where no electron states can exist. Imagine you’re at an amusement park with lots of different rides. Some rides are on the ground level, and some are high up in the air. Now, think of the ground-level rides as the Valence Band, where most people (electrons) are. The high-up rides are the Conduction Band, where people can see everything and move around freely.
The Forbidden Band is like the space between the ground-level and high-up rides. It’s an area where there are no rides—no place for people to be. In the same way, the Forbidden Band is an energy range in a solid where no electron states exist. Electrons can’t stay in this gap; they have to either be in the Valence Band or jump up to the Conduction Band.
The size of the Forbidden Band (also known as the band gap) tells us how much energy it takes for an electron to make that big jump. If the band gap is large, like the space between low and high rides, it’s hard for electrons to jump up, and the material is likely an insulator. But if the band gap is small, it’s easier for electrons to move up to the Conduction Band, and the material might be a semiconductor.
How does doping affect the band gap?
Doping is a process used in semiconductor physics to alter the electrical properties of materials. When a semiconductor is doped, impurities are intentionally introduced into its crystal lattice. These impurities can affect the band gap in the following ways:
- P-type Doping: This involves adding elements with one less valence electron than the semiconductor material, such as boron or gallium. These create additional energy levels just above the valence band, which manifest as “holes” or positive charge carriers. The band gap itself remains unchanged, but the presence of holes effectively lowers the energy required for electrons to participate in conduction.
- N-type Doping: This involves adding elements with one more valence electron than the semiconductor, such as phosphorus or arsenic. These create additional energy levels just below the conduction band, providing extra electrons or negative charge carriers. Similar to P-type doping, the band gap doesn’t change, but the extra electrons reduce the energy needed for conduction.
While doping doesn’t alter the band gap’s size, it introduces new energy states within the band gap that make it easier for electrons to move from the valence band to the conduction band, thus enhancing the material’s conductivity.
Insulators
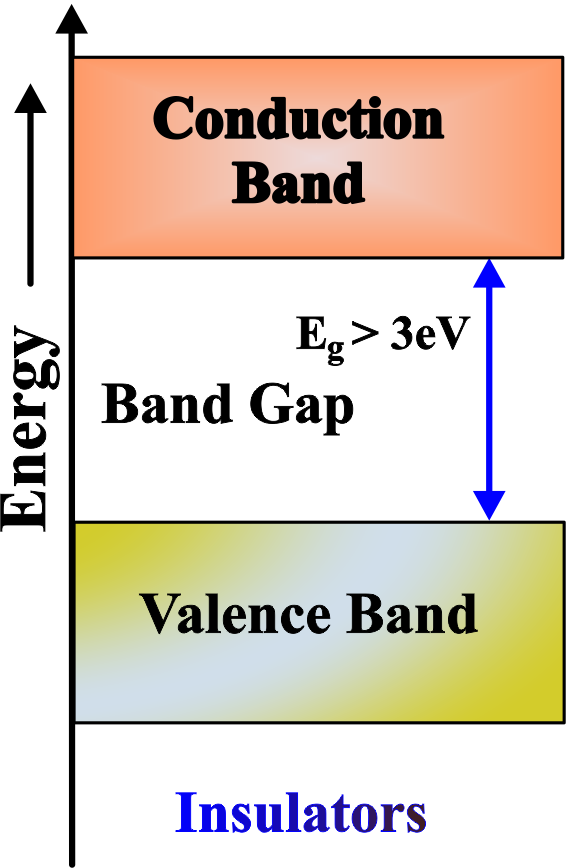
The size of the band gap in insulators can vary depending on the material, but it is generally several electronvolts (eV). For example, diamond, which is an insulator, has a band gap of about 5.5 eV. This large band gap means that under normal conditions, the electrons in the valence band do not have enough energy to cross over into the conduction band, and as a result, insulators do not conduct electricity. The conductivity of an insulator is very low and almost negligible.
Imagine a library with many shelves filled with books. The books on the lower shelves are easy to reach, while the ones on the top shelf are too high without a ladder. In this analogy, the library is the solid, the books are the energy levels, and the ladder is the energy needed to reach higher levels.
In insulators, the Valence Band is like the lower shelves filled with books (electrons). These books are easily accessible (low energy), and they represent the electrons that are bound to the atoms. The Conduction Band is like the top shelf, which is empty because it’s too high to reach without a ladder.
The Forbidden Band, or band gap, is the space between the top of the filled lower shelves and the empty top shelf. In insulators, this gap is very large—like a very tall bookshelf. It’s so large that the electrons (books) can’t jump up to the conduction band (top shelf) under normal conditions because they don’t have enough energy (no ladder).
Because the electrons can’t reach the conduction band, they can’t move freely through the material, which means insulators don’t conduct electricity under normal conditions. The electrons are stuck on the lower shelves, unable to reach the empty top shelf where they would need to be to conduct electricity.
Insulators have a full valence band and a large energy gap to the conduction band, which prevents electrons from moving freely and conducting electricity. It’s like having a library where the top shelf is out of reach, keeping the books (electrons) in place and preventing them from moving around.
Conductors
Conductors have a very small or no band gap, allowing electrons to move freely between the valence and conduction bands.
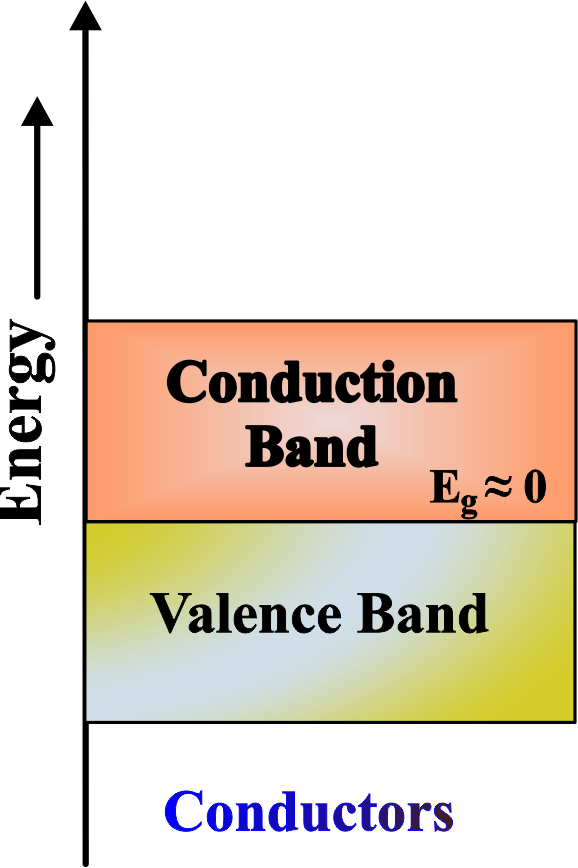
In a conductor, such as a metal, the valence band and the conduction band overlap, so there is no band gap. This means that the electrons can easily move from the valence band to the conduction band and conduct electricity with low resistance.
Think of a busy subway where people can move freely between the cars. This is like electrons in a conductor, where they can move easily through the material.
In conductors:
- The Valence Band is full of electrons, just like a subway car full of people.
- The Conduction Band is where electrons are free to move and conduct electricity, similar to the subway platform where people can walk freely.
- In conductors, the valence band and conduction band overlap, or the conduction band is partially filled even at zero energy. This means there’s no gap or only a very small gap between them. It’s like the door between the subway car and the platform is always open, allowing people to move freely at any time.
Because there’s no significant gap preventing the electrons from moving, they can easily flow and conduct electricity. This is why materials like copper and silver are excellent conductors—they allow electrons to move freely and carry electrical current with little resistance. Conductors have overlapping energy bands that allow electrons to move freely and conduct electricity, much like an open subway system where passengers can move without barriers.
Semiconductors
Semiconductors have a moderate band gap, allowing electrons to move from the valence to the conduction band at higher temperatures or under external influences.
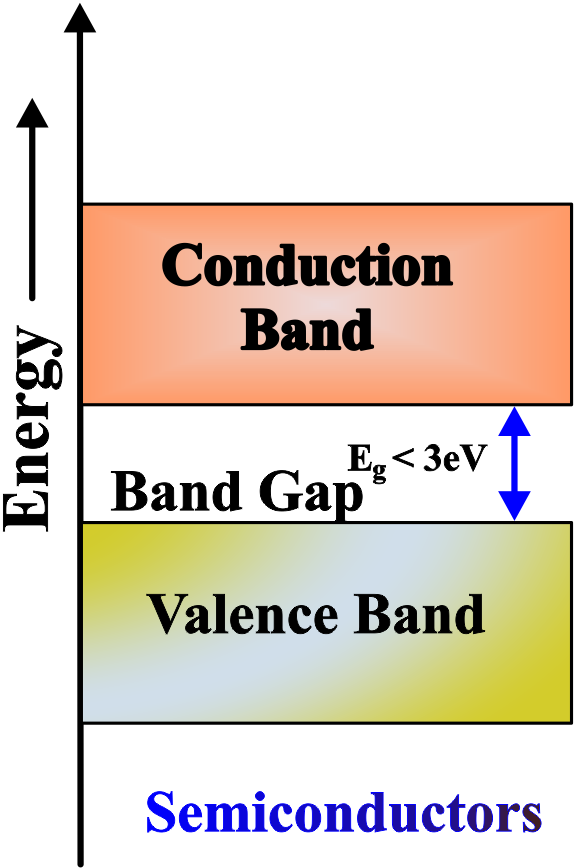
In a semiconductor, such as silicon, the valence band and the conduction band are separated by a small band gap, typically less than 3 eV. This means that the electrons need some external energy, such as heat or light, to jump from the valence band to the conduction band and conduct electricity.
The conductivity of a semiconductor can be controlled by doping, which is the addition of impurities that create extra electrons or holes in the material.
Imagine a staircase where the steps represent energy levels. In solids, these steps merge into ramps or ‘bands’ where electrons can move. Now, semiconductors are like buildings with a staircase that has a small landing or gap between two ramps: the valence band and the conduction band.
In semiconductors:
- The Valence Band is the lower ramp filled with electrons. It’s like the ground floor where most people (electrons) are.
- The Conduction Band is the upper ramp where electrons can move freely, conducting electricity. It’s like an upper floor that’s usually empty.
- The small landing or gap between these two ramps is the Band Gap. In semiconductors, this gap is small enough that some electrons can jump up to the conduction band with a little bit of energy, like a small hop.
At absolute zero temperature, semiconductors behave like insulators with no free electrons in the conduction band. But as the temperature rises or when light is shone on them, electrons gain energy and can hop up to the conduction band, making the semiconductor conductive.
So, semiconductors are special because they can act like insulators sometimes and conductors other times, depending on conditions like temperature and light. This unique property is what makes semiconductors essential in electronic devices like computers and smartphones. They’re like buildings where the upper floors can be reached easily if the conditions are right, allowing people (electrons) to move up and down, enabling the flow of traffic (electricity).
Energy Band Inside An Atom
Inside an atom, electrons occupy discrete energy levels. When atoms are isolated, there are no bands, just individual energy levels. Think of an atom as a tiny solar system. The nucleus is like the sun, and the electrons are like planets orbiting around it. Each electron is at a certain distance from the nucleus, which we can think of as its ‘orbit’. Now, in physics, we don’t call these orbits; we call them energy levels or shells.
Just like planets, electrons can only exist in certain orbits where they are stable. These stable orbits correspond to specific amounts of energy. So, an electron in a closer orbit has less energy, and one in a farther orbit has more energy. These different orbits are the atom’s energy levels.
In an isolated atom, these energy levels are well-defined and discrete, which means there’s a clear energy difference between them. Electrons can jump from one level to another, but they can’t exist in between these levels. It’s like how a planet can move from one orbit to another but can’t just float between orbits.
The Energy Band inside an Atom refers to these discrete energy levels where the electrons can be found. There are no bands in a single atom because the energy levels are not continuous—they’re like distinct steps on a ladder that the electrons can climb up or down.
Energy Levels Inside a Molecule Made up of Two Atoms
When two atoms bond, their energy levels split into bonding and antibonding molecular orbitals, which are the precursor to bands. Imagine two friends, each living in their own house with a ladder. Each rung of the ladder represents an energy level where they can stand. When they are apart, they can only stand on the rungs of their ladders.
Now, when these two friends decide to build a bridge between their houses, they can share the rungs of their ladders. This is similar to what happens when two atoms come close enough to form a molecule. The energy levels (rungs of the ladder) of the two atoms overlap and mix to form new energy levels.
In this new molecular house, there are two types of rungs:
Bonding Orbital:
This is like a reinforced rung that’s more stable and can hold both friends together. Electrons in this orbital help to bond the two atoms together. Imagine two dancers who decide to perform together. When they dance separately, they have their own space and their moves. But when they come together for a duet, they coordinate their movements and create a performance that is more harmonious and graceful than their routines.
In the world of molecules, a Bonding Orbital is like this dance duet. It’s formed when two atomic orbitals from two different atoms overlap constructively. This means that the wave functions of the electrons from these orbitals combine to increase the probability of finding the electrons in the space between the two nuclei.
- Each atom has its own set of orbitals where electrons reside.
- When two atoms come close enough to form a molecule, their outermost orbitals can overlap.
- If the overlap is constructive (meaning the wave functions of the orbitals add together), a Bonding Orbital is formed.
- This new orbital is lower in energy than the original atomic orbitals because it’s more stable.
- Electrons that occupy this bonding orbital are shared between the two atoms, which holds the molecule together.
So, the Bonding Orbital is a shared space created by the overlap of individual atomic orbitals. It’s a region of lower energy where electrons are more likely to be found between the nuclei, creating a stable bond that holds the atoms together in a molecule. It’s like the dancers’ duet, where their coordinated moves (the shared electrons) create a beautiful and stable performance (the molecular bond).
Anti-Bonding Orbital:
This is like a shaky rung that’s less stable. Electrons here can make the molecule less stable. Imagine a school play where two students are supposed to hold a banner together. If they stand close and hold it tight, the banner (bond) is stable—this is like the bonding orbital. Now, if they stand too far apart or pull in opposite directions, the banner sags or might even tear—this represents the anti-bonding orbital.
In molecular terms, an Anti-Bonding Orbital is formed when two atomic orbitals overlap in a way that their wave functions subtract from each other. This creates a space with lower electron density between the two nuclei, known as a nodal plane. Electrons in this orbital are not shared between the atoms; instead, they are more likely to be found outside the space between the nuclei.
- When two atoms come together, their atomic orbitals can overlap destructively as well as constructively.
- The destructive overlap leads to the formation of an anti-bonding orbital, which is higher in energy and less stable than the original atomic orbitals.
- This orbital has a node, a region of zero electron probability, exactly between the nuclei.
- Electrons in the anti-bonding orbital work against the bond, making the molecule less stable.
So, the Anti-Bonding Orbital is like a tug-of-war scenario where the electrons are pulling away from the bond. If a molecule has electrons in an anti-bonding orbital, it means the bond is weaker. If too many electrons end up in anti-bonding orbitals, the molecule might not form at all or could easily break apart. The anti-bonding orbital is a high-energy state that electrons can occupy, which tends to destabilize the bond between atoms.
When two atoms form a molecule, their energy levels combine to create new molecular energy levels where electrons can reside. These new levels are different from the ones in isolated atoms and are crucial for the chemical bonding between the atoms. Just like building a bridge between two houses allows friends to share space, the formation of a molecule allows atoms to share energy levels, creating a stable structure where electrons can live and bond the atoms together.
Energy Levels inside a Molecule Made up of Three Atoms
With three atoms, the splitting of energy levels becomes more complex, leading to a greater number of molecular orbitals. Imagine a trio of musicians, each with their instrument. When they play separately, they each produce their unique notes. But when they come together to form a band, their notes blend to create chords and new harmonies that weren’t there before.
In a molecule with three atoms, something similar happens with energy levels. Each atom has its own set of energy levels when it’s alone. But when three atoms bond together to form a molecule, their energy levels overlap and interact, creating a more complex system of energy levels.
- Individual Atoms: Each atom has its distinct energy levels, like separate musical notes.
- Formation of a Molecule: When three atoms come together, their energy levels begin to overlap.
- New Energy Levels: This overlap results in a set of molecular orbitals that are different from the individual atomic orbitals. There are more energy levels available because there are more interactions between the electrons and the nuclei of the three atoms.
- Bonding and Anti-Bonding Orbitals: Just like in a two-atom molecule, there are bonding orbitals (stable, lower energy) and anti-bonding orbitals (less stable, higher energy). But with three atoms, there are more of these orbitals, and they are more complex.
- Molecular Stability: The way electrons fill these orbitals determines the stability of the molecule. Electrons will first fill the lower energy bonding orbitals, which helps to hold the atoms together.
In a three-atom molecule, the energy levels are like a more complex piece of music with more notes and chords. The electrons can occupy these levels, and their arrangement influences the properties and stability of the molecule.
Also Read: Semiconductor
Energy Levels inside a Solid Made up of Avogadro Number of Atoms
In a solid with Avogadro’s number of atoms, the energy levels split into so many closely spaced levels that they effectively form continuous bands. Imagine a huge stadium filled with a crowd of people. Now, if you look at the stadium from a distance, you can’t see individual people but rather a continuous ‘sea’ of people. This is similar to what happens with energy levels in a solid made up of an Avogadro number of atoms.
In a single atom, there are discrete energy levels where electrons can reside. But when you have as many atoms as Avogadro’s number (approximately \(\displaystyle 6.022 \times 10^{23}\)), the energy levels of these atoms are so closely packed together that they form continuous bands of energy rather than discrete levels.
- Individual Atoms: Each atom has its own set of energy levels, like seats in a stadium.
- Formation of a Solid: When you pack together a huge number of atoms, their energy levels overlap and merge.
- Continuous Energy Bands: With so many overlapping energy levels, they form a continuous range of energy that electrons can occupy, just like the continuous ‘sea’ of people in the stadium.
In a solid with Avogadro’s number of atoms, the energy levels blend into energy bands. These bands are so close together that they appear as a continuum, allowing electrons to move freely within these bands, which is essential for the electrical and thermal properties of the material.
Energy Levels inside a Solid Made up of n-Number of Atoms
As the number of atoms (n) in a solid increases, the number of available energy levels increases, and the difference between them decreases, forming very narrow bands. Think of a large choir where each member sings a different note. If you have only a few singers, you can hear each note. But what if you have a choir with a huge number of singers, say a thousand or more? The notes blend so smoothly that it’s hard to distinguish one from another; it sounds like a continuous harmony.
In a solid, atoms are like the choir members, and their energy levels are like the notes they sing. When you have a solid made up of an ‘n’ number of atoms, each atom contributes its energy levels to the solid. If ‘n’ is a large number, the energy levels from all these atoms overlap and merge to form what we call energy bands.
- Individual Atoms: Each atom has its own set of discrete energy levels.
- Formation of a Solid: When many atoms come together to form a solid, their energy levels start to overlap due to their proximity.
- Energy Bands: As the number of atoms (n) increases, the number of overlapping energy levels increases. If ‘n’ is very large, the energy levels are so closely spaced that they form a continuous range of energy, known as energy bands.
In a solid with many atoms, the individual energy levels blend into broad energy bands. These bands allow electrons to move freely within them, which is crucial for the electrical, thermal, and optical properties of the material.
Energy Levels Inside Material of Different States of Matter
In solids, energy levels form bands. In gases, the atoms are too far apart to form bands. Liquids are intermediate, with some band formation depending on the bonding.
Solid State:
In a solid, atoms are tightly packed together in a fixed arrangement. The energy levels of these atoms overlap to form energy bands. Because the atoms are so close, the bands are very narrow, and the electrons can move through these bands to conduct electricity. It’s like a tightly packed crowd at a concert where everyone is close enough to pass messages (energy) along.
Liquid State:
In liquids, atoms are still close but not in a fixed position—they can move around each other. This means the energy levels are less structured than in solids but more structured than in gases. Electrons in liquids have more freedom to move than in solids, but there’s still some interaction between them. Think of it as a dance floor where people are moving around; they’re not as tightly packed as the concert crowd, but they’re still bumping into each other and exchanging energy.
Gaseous State:
Gases have atoms that are far apart and moving freely. The energy levels in gases are discrete, like in isolated atoms, because there’s little interaction between the atoms. Electrons in a gas are bound to their respective atoms and don’t contribute to electrical conductivity. It’s like people scattered in a large park, each doing their own thing and rarely interacting with others.
Plasma State:
Plasma is like a super-energetic gas. Here, the energy levels are so high that electrons are no longer bound to atoms—they’re free to move around, creating a soup of charged particles. This is the state inside stars, including our sun. In plasma, the energy levels are continuous, and the material is highly conductive.
So, the state of matter affects how the energy levels are organized and how electrons behave, influencing the material’s properties, like electrical conductivity and heat capacity.
Importance of Band Theory of Solids
The Band Theory is crucial because it explains the electrical conductivity of materials. It helps us understand why some materials are conductors, some are insulators, and others are semiconductors.
- Understanding Electrical Properties: Band Theory helps explain why some materials conduct electricity (conductors), why some don’t (insulators), and why some conduct under certain conditions (semiconductors). It’s like knowing why some roads allow traffic to flow freely while others don’t.
- Foundation of Electronics: This theory is the basis for designing and understanding how electronic devices work. We wouldn’t have smartphones, computers, or solar panels without it.
- Explaining Thermal Properties: It also accounts for the thermal properties of materials, like how well they hold or transfer heat, which is essential for creating everything from cookware to spacecraft materials.
- Quantum Mechanics Application: Band Theory is a practical application of quantum mechanics, showing students how these principles shape the real world.
- Material Science: It aids in predicting and explaining the properties of new materials, which is vital for developing new technologies.
Solved Examples
Problem 1: Silicon (Si) is a semiconductor with an energy band gap of 1.1 eV. If the temperature is increased from 300 K to 600 K, what is the approximate change in the intrinsic carrier concentration in silicon? Assume the effective density of states in the conduction and valence bands remain constant with temperature.
Solution: The intrinsic carrier concentration (ni) in a semiconductor is given by:
\(\displaystyle n_i = \sqrt{N_c N_v} e^{-\frac{E_g}{2kT}} \)
Since (Nc) and (Nv) remain constant with temperature, we can write:
\(\displaystyle \frac{n_{i2}}{n_{i1}} = e^{-\frac{E_g}{2kT_2}} / e^{-\frac{E_g}{2kT_1}} = e^{-\frac{E_g}{2k} (\frac{1}{T_2} – \frac{1}{T_1})} \)
Given:
- (\(\displaystyle E_g = 1.1 \text{ eV} = 1.1 \times 1.6 \times 10^{-19} \text{ J} = 1.76 \times 10^{-19} \text{ J}\))
- (\(\displaystyle k = 1.38 \times 10^{-23} \text{ J/K}\))
- (\(\displaystyle T_1 = 300 \text{ K}\))
- (\(\displaystyle T_2 = 600 \text{ K}\))
Plugging in the values:
\(\displaystyle \frac{n_{i2}}{n_{i1}} = e^{-\frac{1.76 \times 10^{-19}}{2 \times 1.38 \times 10^{-23}} (\frac{1}{600} – \frac{1}{300})} \)
Simplifying inside the exponent:
\(\displaystyle \frac{1}{600} – \frac{1}{300} = -\frac{1}{600} \)
\(\displaystyle \frac{1.76 \times 10^{-19}}{2 \times 1.38 \times 10^{-23} \times 600} = \frac{1.76}{1.656 \times 600} = 1.76 \times 10^3 / 993.6 = 1.77 \)
Thus: \(\displaystyle \frac{n_{i2}}{n_{i1}} = e^{1.77} \approx 5.87 \). So, the intrinsic carrier concentration in silicon increases by a factor of approximately 5.87 when the temperature increases from 300 K to 600 K.
Problem 2: Consider a molecule consisting of two identical atoms. The energy levels of the molecule can be approximated by the linear combination of atomic orbitals (LCAO). If the energy difference between the bonding and antibonding orbitals is 2 eV, what is the energy of each molecular orbital if the atomic orbitals have an energy of -10 eV?
Solution: In a diatomic molecule, the bonding and antibonding molecular orbitals are formed from the combination of atomic orbitals. The bonding orbital will have lower energy, and the antibonding orbital will have higher energy.
Given:
- Energy difference between bonding and antibonding orbitals = 2 eV
- Energy of atomic orbitals = -10 eV
Let’s denote the energy of the bonding orbital as (Eb) and the antibonding orbital as (Ea).
We have: \(\displaystyle E_a – E_b = 2 \text{ eV} \)
Since the bonding orbital has lower energy:
\(\displaystyle E_b = -10 \text{ eV} – x \)
\(\displaystyle E_a = -10 \text{ eV} + x \)
Substituting into the energy difference equation:
\(\displaystyle (-10 + x) – (-10 – x) = 2 \)
\(\displaystyle x + x = 2 \)
\(\displaystyle 2x = 2 \)
\(\displaystyle x = 1 \)
Therefore:
\(\displaystyle E_b = -10 \text{ eV} – 1 = -11 \text{ eV} \)
\(\displaystyle E_a = -10 \text{ eV} + 1 = -9 \text{ eV} \)
The energy of the bonding orbital is -11 eV, and the energy of the antibonding orbital is -9 eV.
Problem 3: For a triatomic molecule with atoms in a line, the molecular orbitals can be constructed from the atomic orbitals. If the atomic orbital energies are -8 eV, -8 eV, and -8 eV, and the interaction energy between adjacent atoms is 1 eV, find the energy levels of the molecular orbitals.
Solution: In a triatomic molecule, the molecular orbitals can be found using the linear combination of atomic orbitals (LCAO) method. For simplicity, consider the molecule to be symmetric.
Given:
- Atomic orbital energies: (-8 eV)
- The interaction energy between adjacent atoms: (1 eV)
The molecular orbitals formed will have different energy levels due to the interaction. For three atoms, the molecular orbital energies are given by:
\(\displaystyle E_1 = E_0 – 2\beta \)
\(\displaystyle E_2 = E_0 \)
\(\displaystyle E_3 = E_0 + 2\beta \)
Where (E0) is the energy of the atomic orbitals, and (\beta) is the interaction energy.
Given:
\(\displaystyle E_0 = -8 \text{ eV} \)
\(\displaystyle \beta = 1 \text{ eV} \)
So, the energy levels are:
\(\displaystyle E_1 = -8 \text{ eV} – 2 \times 1 \text{ eV} = -10 \text{ eV} \)
\(\displaystyle E_2 = -8 \text{ eV} \)
\(\displaystyle E_3 = -8 \text{ eV} + 2 \times 1 \text{ eV} = -6 \text{ eV}\)
Thus, the energy levels of the molecular orbitals are -10 eV, -8 eV, and -6 eV.
Problem 4: Consider a solid made up of (N) atoms. The energy levels in a solid form bands due to the overlap of atomic orbitals. If the energy gap between the valence band and the conduction band is 1.5 eV and the temperature is 300 K, calculate the probability that an electron is in the conduction band (use the Boltzmann approximation).
Solution: The probability that an electron is in the conduction band can be found using the Boltzmann factor, which gives the probability of an electron having enough energy to jump the gap.
Given:
- Energy gap (Eg) = 1.5 eV
- Temperature (T) = 300 K
- Boltzmann constant (k) = (\(\displaystyle 8.617 \times 10^{-5} \text{ eV/K}\))
The probability (P) is given by:
\(\displaystyle P = e^{-\frac{E_g}{kT}} \)
Substitute the values:
\(\displaystyle P = e^{-\frac{1.5 \text{ eV}}{8.617 \times 10^{-5} \text{ eV/K} \times 300 \text{ K}}} \)
\(\displaystyle P = e^{-\frac{1.5}{0.025851}} \)
\(\displaystyle P = e^{-58.02} \)
The exponential of a large negative number is very small, hence:
\(\displaystyle P \approx 0 \)
The probability that an electron is in the conduction band at 300 K is negligible.
FAQs
What are energy bands in solids and how do they form?
Energy bands in solids are ranges of energy that electrons can have within a material. They form due to the overlap of atomic orbitals when a large number of atoms come together to form a solid. As atoms approach each other, their discrete energy levels split and merge, creating continuous bands of energy levels. The most important bands are the valence band, filled with electrons, and the conduction band, which can accept electrons.
How do energy bands differ inside an atom compared to a solid?
Inside an isolated atom, electrons occupy discrete energy levels corresponding to specific orbitals. In a solid, however, the interactions between a large number of atoms cause these discrete levels to broaden into continuous energy bands. This transformation is due to the quantum mechanical interactions and the Pauli exclusion principle, which prevents electrons from occupying the same quantum state.
What are the energy levels like inside a molecule made up of two atoms?
In a molecule made up of two atoms, the individual atomic orbitals combine to form molecular orbitals. These molecular orbitals have different energy levels depending on whether they are bonding, antibonding, or non-bonding. The energy levels in a diatomic molecule are thus more complex than those in a single atom, reflecting the interaction between the two atomic nuclei and their electrons.
How do energy levels change inside a molecule made up of three atoms?
For a molecule made up of three atoms, the energy levels become even more complex. The atomic orbitals of the three atoms combine to form molecular orbitals, which split into different energy levels. The specific arrangement and energy of these levels depend on the type of atoms involved and their bonding. These levels determine the molecule’s electronic properties and behavior.
How are energy levels structured inside a solid made up of Avogadro’s number of atoms?
In a solid composed of Avogadro’s number of atoms, the energy levels of individual atoms merge into continuous energy bands due to the immense number of overlapping atomic orbitals. These bands can be divided into the valence band, conduction band, and sometimes a forbidden bandgap between them. The exact structure and spacing of these bands depend on the material’s atomic structure and bonding.
How do energy levels inside a solid with an n-number of atoms compare to those in a solid with Avogadro’s number of atoms?
The energy levels inside a solid with n-number of atoms will exhibit band formation similar to that in a solid with Avogadro’s number of atoms, but the density of states and the width of the bands will differ based on n. As n increases, the bands become more defined and continuous, approaching the characteristics seen in macroscopic solids. For smaller n, the energy levels might retain more discrete characteristics, especially in nanomaterials.
How do energy levels inside materials differ across different states of matter?
The energy levels inside materials vary significantly across different states of matter. In solids, energy levels form continuous bands due to strong interactions between atoms. In liquids, the energy levels are more discrete but can still exhibit some band-like features due to proximity and interaction of molecules. In gases, the energy levels are mostly discrete, with minimal interaction between atoms or molecules. The state of matter affects the electronic properties, conductivity, and other physical characteristics of the material.