Acceleration

The concept of acceleration has been pivotal in physics, dating back to the works of Galileo Galilei and Sir Isaac Newton. Galileo Galilei’s work on acceleration was a significant departure from the prevailing Aristotelian physics of his time. Aristotle claimed that an object’s fall speed depended on its weight and the medium it was falling through. However, Galileo, through his experiments and thought processes, challenged this view.

Galileo faced a dilemma: how to measure the acceleration of objects when they fall so quickly. He needed to understand the relationship between the time an object took to fall and the distance it covered. The challenge was that the tools of his time could not accurately measure the rapid descent of freely falling objects.

To solve this, Galileo devised an ingenious experiment using an inclined plane. By rolling balls down the plane, he could slow down the acceleration enough to make precise measurements. He observed that a ball rolling down the plane would cover more distance in the second interval of time than it did in the first, even though each interval was the same duration. This meant that the ball was accelerating—it was picking up speed as it rolled further down the plane.

Through meticulous observation and timing, he discovered a fascinating fact: the distance an object traveled was directly proportional to the square of the time it had been moving. This was a groundbreaking realization, as it laid the foundation for the concept of accelerated motion.

Galileo’s work laid the foundation for Newton’s laws of motion and the modern understanding of acceleration. His approach to solving the dilemma of measuring acceleration changed the course of physics and is a classic example of scientific problem-solving.

But the story doesn’t end there. Enter Sir Isaac Newton, a giant in the world of science. Newton pondered upon the question of why objects accelerate. He realized that to explain the workings of the universe, he needed to introduce the concept of a force. With his second law of motion, Newton elegantly demonstrated that acceleration is the result of an unbalanced force acting on an object. This could be a push or a pull, but the most familiar force we experience every day is gravity. Newton showed that gravity is, in fact, a type of acceleration, that influences the mass of objects to produce what we feel as weight.

These insights from Galileo and Newton have shaped our understanding of the physical world and remain fundamental to physics education today. They teach us that acceleration isn’t just about how fast something is moving, but how its movement changes over time, and that forces are the invisible hands that shape this change.

What Is Acceleration?

Acceleration is a fundamental concept in physics that describes how an object’s motion changes over time. It’s not just about speed, but about the rate at which speed changes. Acceleration is the rate at which an object’s velocity changes over time. It’s not just about speed; it’s also about direction. If an object speeds up, slows down, or changes direction, it’s accelerating.

Think about riding a bike. When you start pedaling, you move from a standstill to a certain speed – you’re accelerating. If you pedal harder, your speed increases more quickly, and your acceleration is greater. Now, if you stop pedaling and start applying the brakes, you’re also accelerating, but in the opposite direction, because your speed is decreasing.

Imagine you’re hiking up a hill. The steeper the hill, the harder it is to climb. In this analogy, the steepness of the hill is like acceleration. Just as a steeper hill means a quicker increase in elevation, a higher acceleration means a quicker change in velocity.
OR
we say that an object accelerates if its velocity changes: it can be speeding up, slowing down, or changing direction. For Example:

• Speeding Up: A car increasing its speed from 30 km/h to 60 km/h is accelerating.
• Slowing Down: The same car coming to a stop is also accelerating but in the opposite direction of its motion.
• Changing Direction: Even if the car keeps a constant speed but turns a corner, it’s still accelerating because its direction is changing.

Acceleration is a vector quantity, which means it has both magnitude and direction. This is why changing direction, even while maintaining a constant speed, is still considered acceleration. For example, when a car turns a corner at a steady speed, it’s accelerating because the direction of its velocity is changing.

Mathematically, acceleration is defined as the rate of change of velocity with respect to time. It’s the “speed of the speed” – how quickly the velocity is changing. The formula for acceleration is:

\(\displaystyle\begin{equation}\label{eqn:1}\boxed{\boldsymbol{ a = \frac{\Delta v}{\Delta t}}} \end{equation}\)

where (a) is acceleration, (∆v) is the change in velocity, and (∆t ) is the change in time.

In physics, we measure acceleration in meters per second squared (m/s²). This unit tells us how much an object’s velocity changes every second.

It’s about the feeling you get when you push the gas pedal in a car, the tug you feel when the subway starts moving, or the pull you experience when an airplane takes off. These are all instances of acceleration.

Acceleration is all about change in motion. Whether it’s speeding up, slowing down, or changing direction, if there’s a change in velocity, there’s acceleration. It’s a measure of how quickly that change is happening, and it’s a key concept that helps us describe and predict the motion of objects in our universe.

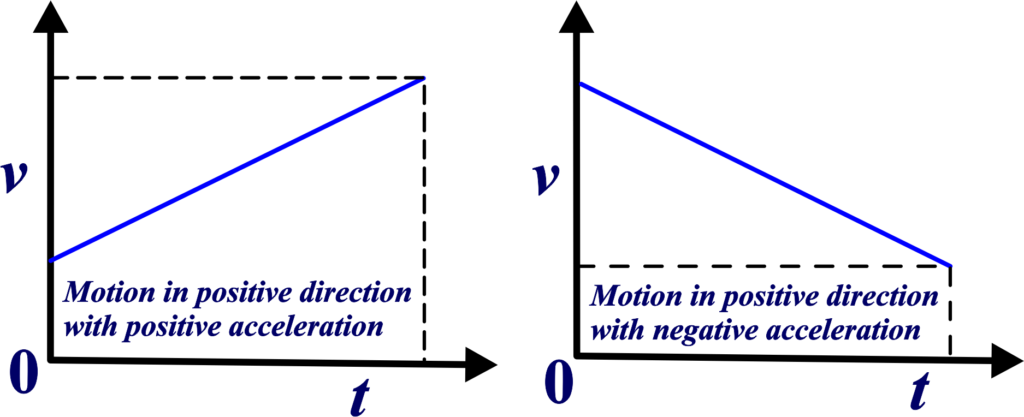
Positive Acceleration:

Positive acceleration is a term used when an object’s speed increases in the direction it’s moving.  Positive acceleration means that an object is getting faster. For example, when a car accelerates from a stop sign, its speed increases, and this is positive acceleration.

Positive acceleration doesn’t just mean moving forward. It can occur in any direction. For example, if you’re driving in reverse and press the gas pedal to increase your speed, you’re still experiencing positive acceleration, even though you’re moving backward. When discussing positive acceleration, the value will be positive because the velocity is increasing. On a velocity-time graph, positive acceleration is shown by a line sloping upwards, indicating an increase in velocity over time.

Negative Acceleration:

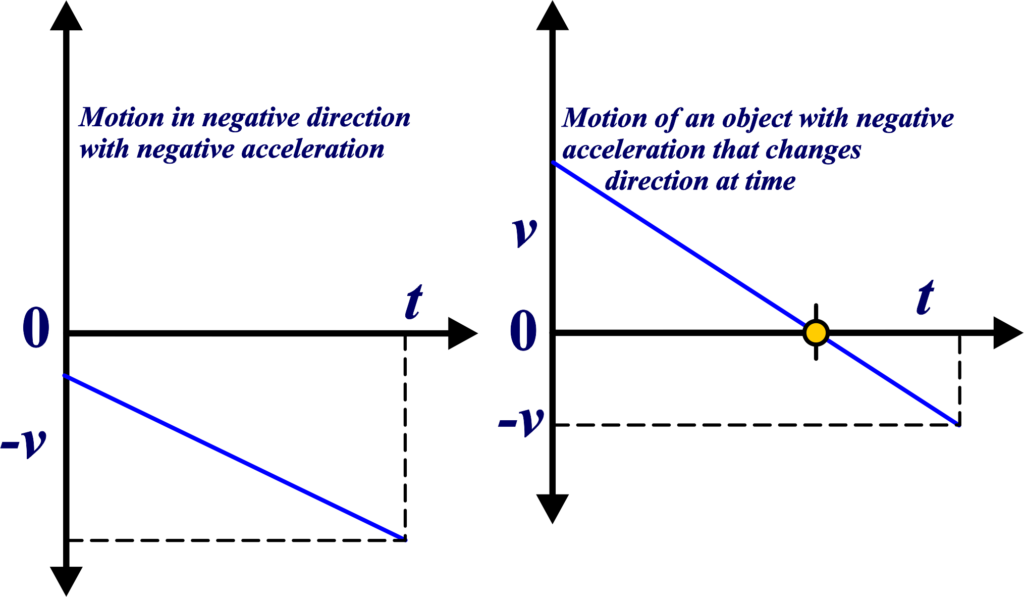
Negative acceleration, often referred to as deceleration occurs when an object’s velocity decreases over time. In simpler terms, it’s when something slows down. Negative acceleration is a crucial concept in physics that helps us understand how objects move when they lose speed.

Negative acceleration means that an object is getting slower. For example, when a car applies its brakes to come to a stop, its speed decreases, and this is negative acceleration. Negative acceleration doesn’t mean moving backward; it simply means the object is losing speed.

For instance, if you’re driving forward and gradually eased off the gas pedal, causing your car to slow down, you’re experiencing negative acceleration, even though you’re still moving in the forward direction. When discussing negative acceleration, the value will be negative because the velocity is decreasing.

Example: A common example is a ball thrown upwards. As it rises, it slows down due to gravity, which is acting in the opposite direction to its initial motion. This slowing down is negative acceleration.

Also Read: Position, Path Length And Displacement

Types of Acceleration

There are different types of acceleration based on how velocity changes over time:

Uniform Acceleration

Uniform acceleration occurs when an object’s velocity changes by the same amount in every equal interval of time. In simpler terms, it’s when something speeds up or slows down by a consistent amount over time.

Uniform acceleration means that the change in velocity is constant. Whether an object is speeding up or slowing down, the rate at which it accelerates remains the same. Uniform acceleration commonly occurs in situations where an object moves in a straight line, like a car accelerating along a road or a ball falling under gravity. We can represent uniform acceleration mathematically using equations. Uniform acceleration is described by three key equations of motion:

\(\displaystyle\begin{equation}\label{eqn:2}\boxed{\boldsymbol{\begin{aligned}
&v = u + at \\
& s = ut + \frac{1}{2}at^2 \\
& v^2 = u^2 + 2as
\end{aligned} }} \end{equation}\)

• (v) is the final velocity,
• (u) is the initial velocity,
• (a) is the acceleration,
• (s) is the displacement,
• (t) is the time interval.

Characteristics

• In uniformly accelerated motion, the acceleration remains constant throughout the motion. This means that the rate of change of velocity is the same at all times.
• Due to the constant acceleration, the change in velocity of the object is linearly proportional to the time elapsed. This means that the velocity increases or decreases by the same amount in equal intervals of time.
• The displacement of the object changes linearly with time during uniformly accelerated motion. This means that the distance traveled by the object increases or decreases at a constant rate over time.
• In a velocity-time graph, uniformly accelerated motion is represented by a straight line with a slope equal to the acceleration. In a displacement-time graph, it forms a parabola
• In uniformly accelerated motion, the speed of the object either increases uniformly if the acceleration is in the direction of motion, or decreases uniformly if the acceleration is opposite to the direction of motion.
• Uniformly accelerated motion typically occurs in a straight line, although the direction of motion may change if there is a change in acceleration.
• The motion of an object undergoing uniformly accelerated motion can be described using mathematical equations derived from the equations of motion. These equations relate the initial velocity, final velocity, acceleration, displacement, and time.
• The acceleration is independent of the mass of the object. This is evident from the fact that all objects in free fall near the Earth’s surface have the same acceleration due to gravity, regardless of their mass.

Examples:

• A car accelerates from rest at a traffic light with a constant rate of acceleration.
• A ball drops from a certain height and accelerates downwards due to gravity.
• A rocket takes off from the ground and steadily increases its velocity as it ascends.

Imagine a car starting from a standstill at a traffic light. As the driver presses the accelerator, the car’s velocity increases at a constant rate. Each second, it might add the same amount of speed until it reaches the desired velocity. This consistent increase in speed over time is uniform acceleration.

Non-uniform Acceleration

Non-uniform acceleration occurs when an object’s acceleration changes over time. In other words, the rate at which the object’s velocity changes is not constant. It can speed up or slow down at different rates at different times.

Imagine driving a car that speeds up gradually as you press the gas pedal. At first, the car’s acceleration is high, but as it reaches higher speeds, the acceleration decreases until it levels off. This changing rate of acceleration is an example of non-uniform acceleration.

Non-uniform acceleration describes the situation where an object’s acceleration changes over time. Unlike uniform acceleration, where the rate of change of velocity remains constant, non-uniform acceleration involves variable rates of change in velocity. Understanding non-uniform acceleration helps us analyze more complex motion scenarios where acceleration is not constant.

Characteristics

• In non-uniform acceleration motion, the acceleration of the object changes over time. This means that the rate at which the object’s velocity changes is not constant.
• Due to the changing acceleration, the change in velocity of the object is not consistent. It can increase or decrease by different amounts in equal intervals of time.
• On a velocity-time graph, non-uniform acceleration appears as a curved line rather than a straight line. This curvature indicates that the rate of change of velocity is not constant over time.

Non-uniform acceleration occurs in various real-world situations:

• When a car starts from rest and gradually accelerates to reach a certain speed, its acceleration is initially high but decreases as it approaches its final velocity.
• When a rocket takes off from the ground, its acceleration may increase as it burns more fuel and decreases as it ascends further into space.
• In non-uniform acceleration motion, the object’s speed changes at a varying rate. It can speed up or slow down over time, depending on the changing acceleration.
• Non-uniform acceleration motion can be described using mathematical equations that account for the changing acceleration over time. These equations may involve calculus to calculate the exact changes in velocity and displacement.

Average Acceleration

Average acceleration is the total change in velocity divided by the total time taken for that change. When we talk about acceleration, we’re usually referring to how quickly an object is speeding up or slowing down. But often, the rate of this speed change isn’t constant. That’s where average acceleration comes in—it’s a way to describe the overall rate of speed change over a period of time.

Think about a car trip you might take. When you start your car, you accelerate to get up to speed, then you might slow down for a traffic light, and later speed up again on the highway. Your acceleration during this trip isn’t constant; it changes. So, if we want to talk about your car’s acceleration over the entire trip, we use average acceleration.

The formula for average acceleration is pretty straightforward:

\(\displaystyle a_{avg} = \frac{\Delta v}{\Delta t} \)

• (a_avg ) is the average acceleration,
• (∆v ) is the change in velocity,
• (∆ t ) is the total time over which this change occurs.

Average acceleration tells us how much the velocity of an object has changed, on average, every second over a certain time period. It’s like the average pace of a runner over a race—not too fast, not too slow, but the average speed from start to finish.

Example: Let’s say you’re watching a drag race. The race cars speed up rapidly at the start, but their acceleration decreases as they reach higher speeds. By calculating the average acceleration, we can get a sense of how quickly the cars increased their speed throughout the race, even though the rate of acceleration wasn’t the same the whole time.

Average acceleration is particularly useful when dealing with non-uniform acceleration. It gives us a simple number that represents the general rate of speed change, even when that rate isn’t constant. It’s like looking at the average speed of a marathon runner—it doesn’t tell you about the sprints and slowdowns, but it does give you a good idea of the overall pace.

Instantaneous Acceleration

Instantaneous acceleration is the acceleration of an object at a specific moment in time. It’s the exact rate of change of velocity at that instant, calculated using calculus as the derivative of velocity with respect to time.

Just like taking a picture freezes a moment in time, instantaneous acceleration captures the exact rate of change in velocity of an object at a particular instant. Acceleration is all about changes in velocity. When an object speeds up, slows down, or changes direction, its velocity changes, and the rate at which this change occurs is the instantaneous acceleration. We can calculate instantaneous acceleration using calculus. The formula for instantaneous acceleration (a) is the derivative of velocity (v) with respect to time (t):

\(\displaystyle a = \frac{{dv}}{{dt}}\)

To find instantaneous acceleration, we use calculus because it allows us to examine the change in velocity over an infinitesimally small interval of time. This is like zooming in on the speedometer of the car at a particular second and seeing how much the needle moves in that brief moment.

\(\displaystyle a=\frac{d}{{dt}}\left( {\frac{{dx}}{{dt}}} \right)=\frac{{{{d}^{2}}x}}{{d{{t}^{2}}}}\)

Example: A practical example would be a ball thrown into the air. As it goes up and comes down, its speed changes every moment due to gravity. The instantaneous acceleration at any point during its flight can tell us the exact rate at which its speed is increasing or decreasing.

• When a car accelerates rapidly to pass another vehicle on the highway.
• When a skateboarder changes direction suddenly while riding down a street.

Instantaneous acceleration gives us a precise understanding of how an object’s velocity is changing at any given moment. It’s like taking a detailed snapshot of motion to analyze how fast things are speeding up or slowing down at a specific instant.

FAQs