Relative Velocity

The concept of relative velocity is deeply rooted in the history of physics and our understanding of motion. It’s a concept that has evolved, influenced by the work of many great scientists.

Galileo Galilei was one of the first to discuss the idea of relativity in motion. He proposed that motion is relative — meaning that an object’s movement can only be defined relative to something else. For example, if you’re sitting in a train moving at a constant speed, you appear to be at rest relative to other passengers, but you’re moving relative to someone standing outside.

This idea was revolutionary because it contradicted the common belief of the time that there was an absolute state of rest, against which all motion could be measured. Galileo’s insights laid the groundwork for Isaac Newton’s laws of motion, further developing the concept of relative motion.

In Newtonian mechanics, the relative velocity between two objects depends on their velocities with respect to a common frame of reference. This is often referred to as the Galilean transformation. It’s a mathematical principle that allows us to transform the coordinates of one reference frame to another that is moving at a constant velocity relative to the first.

However, the Galilean transformation assumes that speeds are much less than the speed of light. This assumption holds for everyday experiences but falls apart at very high speeds. The limitations of Galilean transformations led to Albert Einstein’s theory of special relativity, which redefined the concepts of space and time and introduced the idea that the speed of light is the same for all observers, regardless of their relative motion.

What is Relative Velocity?

Relative velocity is a fundamental concept in physics that describes the velocity of an object as observed from another moving reference frame.

In the simplest terms, relative velocity is how fast and in what direction one object is moving as seen from another object in motion. It’s a vector quantity, which means it has both magnitude (how fast) and direction (where to).

The core idea behind relative velocity is that motion is not absolute but is always measured relative to something else. There is no universal “stationary” frame of reference; even what we consider to be stationary (like the ground) is moving relative to other things (like the Sun or the galaxy).

Mathematically, relative velocity is calculated by subtracting the velocity vector of one object from the velocity vector of another. If you have two objects, A and B, with velocities \(\displaystyle \vec{V}_{A} \) and \(\displaystyle \vec{V}_{B} \), the relative velocity of A with respect to B is:

\(\displaystyle \vec{V}_{AB} = \vec{V}_A – \vec{V}_B \)

The relative velocity of B with respect to A is:

\(\displaystyle \vec{V}_{BA} = \vec{V}_B – \vec{V}_A \)

An interesting aspect of relative velocity is its symmetry. The magnitude of the relative velocity of A with respect to B is the same as that of B with respect to A, just in the opposite direction.

Imagine you’re on a moving sidewalk at the airport. If you stand still, you’re moving relative to the ground outside. But if you start walking on the moving sidewalk, your speed relative to the ground outside increases. This is the essence of relative velocity.

Let’s say we have two cars, Car A and Car B, driving on a highway. If Car A is going 60 km/h and Car B is going 70 km/h in the same direction, then from the perspective of Car A, it seems like Car B is only going 10 km/h faster than Car A. This “10 km/h” is the relative velocity of Car B with respect to Car A.

Mathematically, we express relative velocity as

\(\displaystyle \vec{V}_{AB} = \vec{V}_{A }- \vec{V}_{B} \),

where \(\displaystyle\vec{V}_{AB} \) is the velocity of object A relative to object B, \(\displaystyle \vec{V}_{A} \) is the velocity of object A, and \(\displaystyle \vec{V}_{B} \) is the velocity of object B.

In a more visual sense, if you were to throw a ball forward while running, the ball’s velocity relative to the ground would be the sum of its velocity relative to you and your velocity relative to the ground. This combined velocity is what an observer on the ground would see.

Understanding relative velocity is crucial because it helps us describe and predict the motion of objects in a way that makes sense from different perspectives. It’s especially important in scenarios where multiple objects are moving, like vehicles on a highway or aircraft in the sky.

Difference between Velocity and Relative Velocity

Velocity is the speed of an object in a given direction, while relative velocity is the velocity of one object as observed from another moving object.

Velocity

Velocity is a vector quantity, which means it has both magnitude (speed) and direction. It tells us how fast an object is moving and in which direction. For example, if a car is moving eastward at 60 km/h, its velocity is 60 km/h east. This is an absolute measure of the object’s motion in relation to a fixed point, like the Earth’s surface.

Relative Velocity

Relative velocity, on the other hand, considers the motion of two objects relative to each other. It’s the velocity of one object as seen from another moving object. If you’re sitting in a car (Car A) moving at 60 km/h and another car (Car B) passes you going 70 km/h in the same direction, Car B’s relative velocity with respect to you (in Car A) is 10 km/h east. This is because from your perspective in Car A, Car B is only moving 10 km/h faster than you.

Key Differences

• Frame of Reference: Velocity is measured with respect to a stationary frame of reference, like the ground. Relative velocity is measured from the perspective of a moving object.
• Comparison: Velocity describes a single object’s motion. Relative velocity compares the motion of two objects.
• Dependence: The velocity of an object is independent of the observer’s motion. Relative velocity depends on the motion of both the observer and the object being observed.

To understand the difference, think of watching a race from the stands versus participating in the race. From the stands, you see the absolute velocity of each racer. But if you’re running in the race, you’re more concerned with the relative velocity—how fast competitors are moving compared to you.

Relative Motion in One Dimension

In one dimension, relative velocity simplifies to the difference in speeds if the objects are moving in the same direction, or the sum if they are moving in opposite directions.

When we talk about relative motion in one dimension, we’re looking at objects moving along a straight line. This could be cars on a road, trains on tracks, or even athletes running a 100-meter dash. The key here is that all movement is restricted to a single straight path.

Objects Moving in the Same Direction

When two objects are moving in the same direction along this line, their relative motion is characterized by a few key points:

• Velocity Vectors: Each object has a velocity vector pointing in the direction of its motion. Since the objects are moving in the same direction, their velocity vectors also point in the same direction.
• Relative Velocity: The relative velocity is a measure of how fast the distance between the two objects is changing. It’s found by subtracting the velocities of the objects.
• Reference Frame: To describe the motion of one object relative to the other, we choose one object to be our reference frame. The motion we describe is then the motion of the second object as seen from the first.

The relative velocity (V_rel) in such scenarios is calculated using the formula:

\(\displaystyle V_{rel} = V_1 – V_2 \)

Where (V₁) and (V₂) are the velocities of the two objects moving in the same direction. The minus sign indicates that we’re subtracting the velocities because the objects are moving parallel to each other.

• No Interaction Assumed: In calculating relative velocity, we’re not assuming any interaction between the objects—just observing their motion.
• Symmetry in Observation: Regardless of which object you choose as your reference frame, the relative velocity will be the same. This symmetry is a fundamental aspect of relative motion in one dimension.

Imagine two runners on a track, Runner A and Runner B. They are both running in the same direction. Runner A is running at a speed of 5 meters per second (m/s), and Runner B is running slightly faster at 6 m/s.

• Runner A’s Perspective: From Runner A’s point of view, it seems like Runner B is only moving away at 1 m/s because Runner A is also moving forward.
• Runner B’s Perspective: From Runner B’s perspective, Runner A is moving backward at 1 m/s, even though Runner A is moving forward.

The relative velocity is simply the difference in their velocities. We can use the formula:

\(\displaystyle V_{AB} = V_{A} – V_{B} \)

• (V_AB) is the relative velocity of Runner B with respect to Runner A.
• (V_A) is the velocity of Runner A.
• ( V_B) is the velocity of Runner B.

So, in our example:

\(\displaystyle V_{AB} = 5 m/s – 6 m/s = -1 m/s \)

The negative sign indicates that Runner B is moving away from Runner A.

To help students visualize this, you can draw a simple diagram showing two points (representing the runners) moving along a line. You can then show how the distance between them increases over time if they maintain their speeds.

This concept is not just for runners on a track. It applies to cars on a road, trains on parallel tracks, or even planets orbiting in space. Whenever two objects are moving in the same direction, their relative velocity is the difference in their speeds.

Objects Moving in Opposite Directions

When two objects are moving in opposite directions along this line, their relative motion is characterized by a few key points:

• Velocity Vectors: Each object has a velocity vector pointing in the direction it’s moving. Since the objects are moving in opposite directions, their velocity vectors point away from each other.
• Relative Velocity: The relative velocity is a measure of how fast the distance between the two objects is changing. It’s found by adding the magnitudes of the individual velocities of the objects.
• Reference Frame: To describe the motion of one object relative to the other, we choose one object to be our reference frame. The motion we describe is then the motion of the second object as seen from the first.

The relative velocity (V_rel) in such scenarios is calculated using the formula:

\(\displaystyle V_{rel} = V_{1 }+ V_{2} \)

Where (V₁) and (V₂) are the velocities of the two objects moving in opposite directions. The plus sign indicates that we’re adding the magnitudes of the velocities because the objects are moving toward or away from each other.

• No Interaction Assumed: It’s important to note that in calculating relative velocity, we’re not assuming any interaction between the objects—just observing their motion.
• Symmetry in Observation: Regardless of which object you choose as your reference frame, the relative velocity will be the same. This symmetry is a fundamental aspect of relative motion in one dimension.

Suppose, Two cars, Car A and Car B, are moving towards each other on a straight road. Car A is moving north at a speed of 50 km/h, and Car B is moving south at a speed of 60 km/h.

• From a Stationary Observer’s Perspective: The observer would see Car A and Car B approaching each other at a combined speed of 110 km/h (50 km/h + 60 km/h).
• From Car A’s Perspective: Car B appears to be approaching at a speed of 110 km/h.
• From Car B’s Perspective: Car A appears to be approaching at a speed of 110 km/h.

The relative velocity in such a case is the sum of the individual velocities of the two objects. Mathematically, it’s expressed as:

\(\displaystyle V_{AB} = V_A + V_B \)

• (V_AB) is the relative velocity of Car B with respect to Car A.
• (V_A) is the velocity of Car A (50 km/h north).
• (V_B) is the velocity of Car B (60 km/h south).

So, in our example:

\(\displaystyle V_{AB} = 50 km/h + 60 km/h = 110 km/h \)

To help students visualize this, you can draw a diagram with two points representing the cars, moving toward each other on a line. You can show how the distance between them decreases over time if they maintain their speeds.

This concept applies to any scenario where objects move towards each other, like two trains on the same track heading for a collision, or even two athletes starting from opposite ends of a track and running towards each other.

Understanding relative motion in one dimension for objects moving in opposite directions is crucial for solving many real-world problems in physics, from simple traffic scenarios to complex astronomical observations.

Also Read: Average Speed and Average Velocity

Relative Velocity in Two Dimensions

In two dimensions, relative velocity involves vector subtraction and can be visualized using vector diagrams. The resultant vector gives the relative velocity.

Relative velocity in two dimensions can be a bit more complex than in one dimension, but it’s a crucial concept for understanding how objects move in our three-dimensional world.

When we talk about relative velocity in two dimensions, we’re considering objects that are not just moving forward and backward but can also move left and right, up and down. This means their paths can cross or diverge in any number of ways.

• Vector Addition: In two dimensions, velocities are vectors, which means they have both magnitude and direction. To find the relative velocity, we use vector addition or subtraction.
• Components of Velocity: Each velocity vector can be broken down into horizontal and vertical components. These components are treated separately and then combined to give the final vector.

To calculate the relative velocity of one object with respect to another, we subtract the velocity vector of one from the other. If object A has a velocity \(\displaystyle\vec{V}_A \) and object B has a velocity \(\displaystyle\vec{V}_B\), then the relative velocity of A with respect to B is:

\(\displaystyle \vec{V}_{AB} = \vec{V}_A – \vec{V}_{B} \)

And the relative velocity of B with respect to A is:

\(\displaystyle \vec{V}_{BA} = \vec{V}_{B} – \vec{V}_{A} \)

• Vector Diagrams: Drawing vector diagrams can help students visualize how the relative velocity is determined. By placing the tail of one vector at the head of the other, we can see the resulting vector that represents the relative velocity.
• Pythagorean Theorem: When the vectors are perpendicular, we can use the Pythagorean theorem to find the magnitude of the relative velocity.

Examples:

• Boats and Rivers: Consider a boat trying to cross a river. The boat has its own velocity, and the river has a current. The actual path of the boat will be a combination of these two velocities.
• Planes and Wind: An airplane flying in a wind has a velocity relative to the air, and the wind has its own velocity. The plane’s path over the ground is the result of these two velocities combined.

Imagine you’re at a park, and you see a squirrel (particle P). You’re standing at a point we’ll call O, and your friend is standing at another point called O’. You both are looking at the same squirrel.

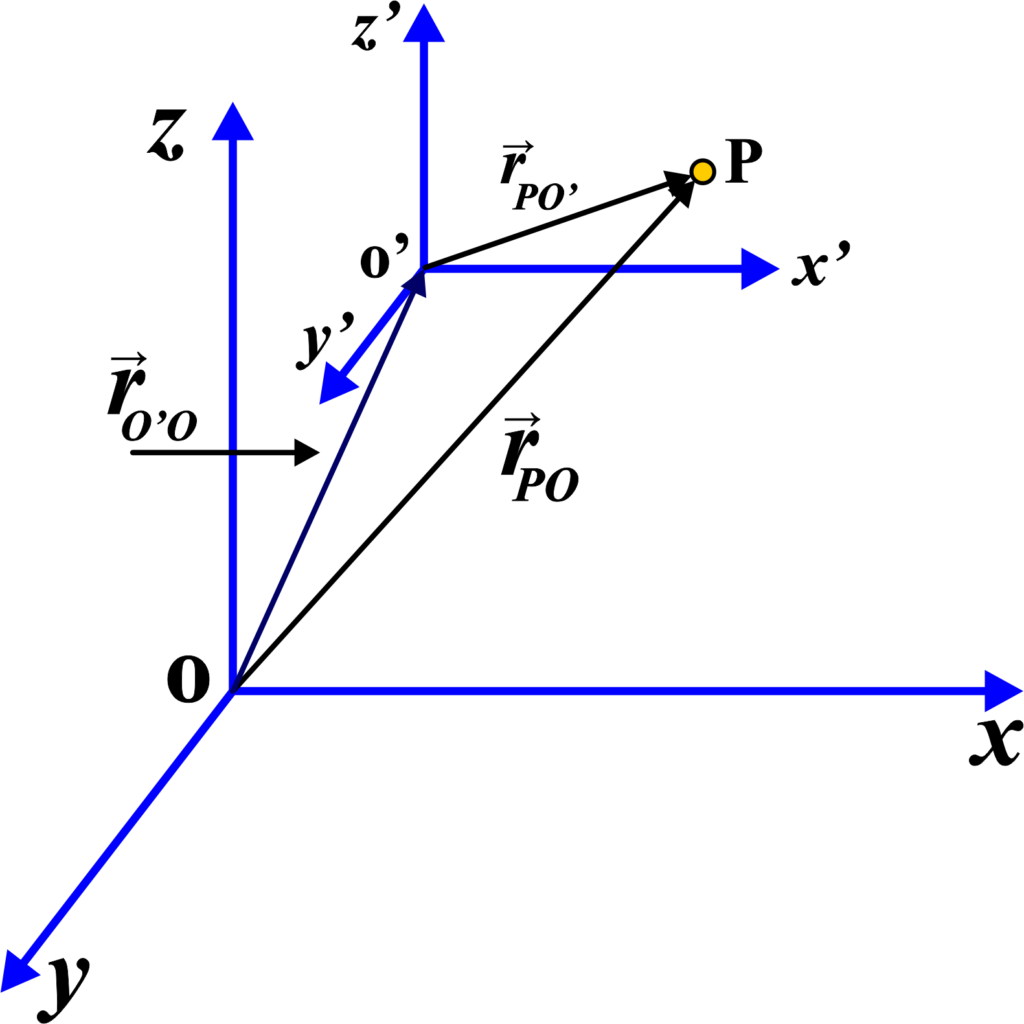
• The position vector \(\displaystyle \overrightarrow{r}_{O’O} \) tells you how to get from your friend’s position (O’) back to your position (O).

To find out where the squirrel is from your point of view, you can use where your friend says the squirrel is and then adjust it to the position of your friend. This is what the equation is saying:

\(\displaystyle \overrightarrow{r}_{PO} = \overrightarrow{r}_{PO’} + \overrightarrow{r}_{O’O} \)

Now, if the squirrel starts moving, it has a velocity. The same idea applies to velocities:

• The velocity vector \(\displaystyle\overrightarrow{v}_{PO} \) is how fast and in what direction the squirrel is moving from your perspective.
• The velocity vector \(\displaystyle \overrightarrow{v}_{PO’} \) is how fast and in what direction the squirrel is moving from your friend’s perspective.
• The velocity vector \(\displaystyle \overrightarrow{v}_{O’O} \) is how fast and in what direction your friend is moving from your perspective.

If the squirrel and your friend start moving, to find out the squirrel’s velocity from your point of view, you take the squirrel’s velocity from your friend’s point of view and adjust it by your friend’s velocity. This is what the second equation is saying:

\(\displaystyle \overrightarrow{v}_{PO} = \overrightarrow{v}_{PO’} + \overrightarrow{v}_{O’O} \)

This means that to understand how fast the squirrel is moving and in which direction from where you’re standing, you need to consider both the squirrel’s movement and your friend’s movement.

Solved Examples

Problem 1: A car A is moving eastward with a speed of 40 km/h and another car B is moving westward with a speed of 60 km/h. Calculate the velocity of car B relative to car A.

Solution:

• Velocity of car A, (v_A = +40 km/h) (eastward)
• Velocity of car B, (v_B = -60 km/h) (westward)

The relative velocity of B with respect to A is given by:

\(\displaystyle v_{BA} = v_B – v_A \)
\(\displaystyle v_{BA} = -60 \, \text{km/h} – 40 \, \text{km/h} \)
\(\displaystyle v_{BA} = -100 \, \text{km/h} \)

The negative sign indicates that car B is moving towards car A at a relative speed of 100 km/h. The velocity of car B relative to car A is 100 km/h westward.

Problem 2: Two trains A and B are moving on parallel tracks in the same direction. Train A moves with a speed of 50 km/h and train B with a speed of 70 km/h. Calculate the relative velocity of train B with respect to train A.

Solution:

• Velocity of train A, (v_A = +50 km/h)
• Velocity of train B, (v_B = +70 km/h)

The relative velocity of B with respect to A is given by:

\(\displaystyle v_{BA} = v_B – v_A \)
\(\displaystyle v_{BA} = 70 \, \text{km/h} – 50 \, \text{km/h} \)
\(\displaystyle v_{BA} = 20 \, \text{km/h} \)

The velocity of train B relative to train A is 20 km/h in the same direction.

Problem 3: A boat is trying to cross a river flowing with a velocity of 3 m/s to the east. The boat’s speed in still water is 4 m/s. Calculate the direction in which the boat should head to reach the point directly opposite to its starting point.

Solution: To counteract the river’s flow, the boat needs to head in a direction upstream. Let the boat’s heading make an angle (θ) with the north direction.

Given:

• Speed of river, (v_r = 3 m/s)
• Speed of boat in still water, (v_b = 4 m/s)

For the boat to reach directly opposite, the eastward component of the boat’s velocity should counter the river’s flow:

\(\displaystyle v_b \sin \theta = v_r \)
\(\displaystyle 4 \sin \theta = 3 \)
\(\displaystyle \sin \theta = \frac{3}{4} \)
\(\displaystyle \theta = \sin^{-1} \left( \frac{3}{4} \right) \)
\(\displaystyle \theta \approx 48.59^\circ \)

The boat should head approximately (48.59^∘) upstream from the north direction to counter the river’s flow.

Problem 4: Two cars are moving in perpendicular directions. Car A moves north at 30 m/s, and car B moves east at 40 m/s. If they are both 100 m from the intersection, will they collide, and if so, in how many seconds?

Solution: First, calculate the time taken by each car to reach the intersection:

• Time for car A: (\(\displaystyle t_A = \frac{100 \, \text{m}}{30 \, \text{m/s}} = \frac{10}{3} \, \text{s} \))
• Time for car B: (\(\displaystyle t_B = \frac{100 \, \text{m}}{40 \, \text{m/s}} = 2.5 \, \text{s} \))

Since (t_B < t_A ), car B reaches the intersection first. Therefore, they will not collide.

The cars will not collide.

Problem 5: A car is moving with a speed of 20 m/s towards the east. Rain falls vertically at a speed of 10 m/s. Calculate the velocity of rain relative to the car.

Solution:

• Velocity of the car, (\(\displaystyle \vec{v}_C = 20 \, \text{m/s}\) ) east
• Velocity of the rain, ( \(\displaystyle\vec{v}_R = 10 \, \text{m/s}\) ) down

Using vector addition, the relative velocity of the rain with respect to the car is:

\(\displaystyle \vec{v}{RC} = \vec{v}_R – \vec{v}_C \) Since the rain falls vertically, and the car moves horizontally, use the Pythagorean theorem:

\(\displaystyle v{RC} = \sqrt{(10 \, \text{m/s})^2 + (20 \, \text{m/s})^2} \)
\(\displaystyle v_{RC} = \sqrt{100 + 400} \)
\(\displaystyle v_{RC} = \sqrt{500} \)
\(\displaystyle v_{RC} = 10\sqrt{5} \, \text{m/s} \)
\(\displaystyle v_{RC} \approx 22.36 \, \text{m/s} \)

To find the angle (θ with respect to the vertical:

\(\displaystyle \tan \theta = \frac{20}{10} = 2 \)
\(\displaystyle \theta = \tan^{-1} 2 \approx 63.43^\circ \)

The velocity of the rain relative to the car is approximately 22.36 m/s at an angle of (63.43^∘) from the vertical.

Problem 6: An airplane is flying north with a speed of 200 km/h relative to the air. There is a wind blowing towards the east at 50 km/h. Calculate the resultant velocity of the airplane with respect to the ground.

Solution:

• Velocity of airplane relative to air, (\(\displaystyle \vec{v}_{PA} = 200 \, \text{km/h} \)) north
• Velocity of wind, (\(\displaystyle \vec{v}_W = 50 \, \text{km/h} \)) east

Using vector addition to find the resultant velocity of the airplane with respect to the ground (( \vec{v}{PG} )):

\(\displaystyle v{PG} = \sqrt{(200 \, \text{km/h})^2 + (50 \, \text{km/h})^2} \)
\(\displaystyle v_{PG} = \sqrt{40000 + 2500} \)
\(\displaystyle v_{PG} = \sqrt{42500} \)
\(\displaystyle v_{PG} \approx 206.16 \, \text{km/h} \)

To find the angle ( \theta ) with respect to north:

\(\displaystyle \tan \theta = \frac{50}{200} = 0.25 \)
\(\displaystyle \theta = \tan^{-1} 0.25 \approx 14.04^\circ \)

The resultant velocity of the airplane with respect to the ground is approximately 206.16 km/h at an angle of (14.04^∘) east of north.

FAQs