The concept of force has been a part of human curiosity for centuries. The modern understanding of forces in mechanics largely stems from the work of Sir Isaac Newton, who, in the 17th century, formulated the three laws of motion that describe how objects interact with forces. These laws laid the foundation for classical mechanics, which is still used to describe most everyday phenomena involving motion and forces.
Long before the term “physics” was coined, ancient civilizations were aware of forces. They observed the effects of gravity, although they couldn’t explain it scientifically. They built structures, used tools, and created machines that utilized mechanical forces.
The Renaissance period marked a significant advancement in the understanding of forces. Engineers began designing complex machines, and the need to understand forces became more apparent. The direction of ropes in pulley systems, for example, indicated the direction of the force being applied, leading to a clearer concept of force vectors.
The real breakthrough came with Sir Isaac Newton in the 17th century. His three laws of motion and the law of universal gravitation provided a comprehensive framework for understanding forces. Newton’s work allowed us to calculate the effects of forces and predict the motion of objects with remarkable accuracy.
With the advent of the Industrial Revolution, the study of forces became even more critical. Machines were everywhere, and understanding how forces worked was essential for innovation and safety. The concepts of tension, friction, and other forces were refined during this period.
Today, we understand forces as interactions that can cause an object to accelerate. They can be categorized into contact forces (like friction and tension) and non-contact forces (like gravity). We also recognize that at the microscopic level, these forces arise from electromagnetic interactions between particles.
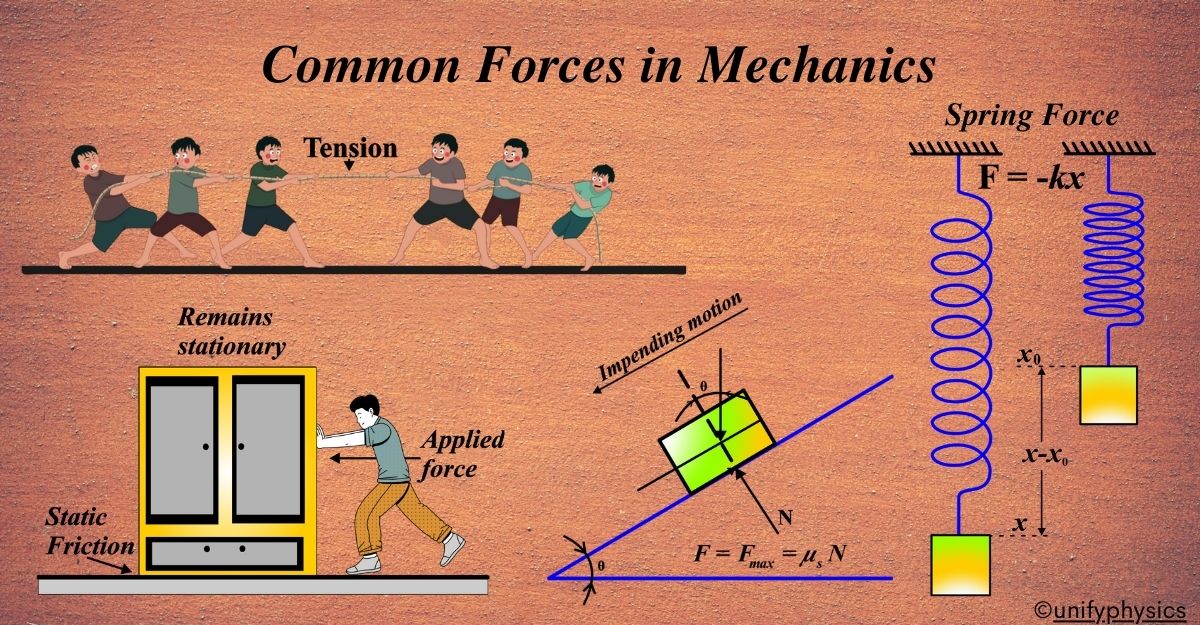
Types of Common Forces in Mechanics
In mechanics, forces can be broadly categorized into two types: contact forces and non-contact forces. Contact forces require physical contact between two objects, while non-contact forces act over a distance without direct contact.
Physics is all about understanding how things move and interact, and forces are what make this happen. Here are some of the most common forces that you’ll encounter in mechanics:
Contact Forces: These are the forces that occur when two objects are physically touching each other.
- Friction: This is the force that resists the motion of two surfaces sliding against each other. It’s why you can walk without slipping and why brakes can stop a car.
- Tension: When you pull on a rope, the rope pulls back with a force called tension. It’s what keeps a swing hanging from a tree or a climber secured to a mountain.
- Normal Force: This is the force that a surface exerts to support the weight of an object resting on it. It’s why a book stays on a table without falling through.
Non-Contact Forces: These forces can act even when objects aren’t touching.
- Gravitational Force: The force of attraction between two masses. It’s what keeps the planets orbiting the sun and what pulls you back down when you jump.
- Electromagnetic Force: This includes forces due to electric charges and magnets. It’s why a magnet sticks to your fridge and why electricity can flow through wires.
- Nuclear Forces: These are extremely strong forces that act at very short distances within the nucleus of an atom.
Special Forces: Some forces don’t fit neatly into the above categories but are still important in mechanics.
- Spring Force: When you compress or stretch a spring, it exerts a force to try to return to its original shape. This is described by Hooke’s Law, where the force is proportional to the displacement.
- Drag Force: This is the resistance force caused by an object moving through a fluid (like air or water). It’s why it’s harder to walk against a strong wind and why streamlining cars and planes is important.
- Pseudo Force: This is a force that appears to act on a mass within a non-inertial frame of reference, like the force you feel pushing you into your seat when a car accelerates.
Friction Force
Friction is a contact force that opposes the relative motion between two surfaces in contact. Imagine you’re trying to push a heavy box across the floor. You push and push, but it takes a lot of effort to get the box moving and to keep it moving. This resistance you feel is due to a force called friction.
Friction is a force that opposes the relative motion between two surfaces in contact. It’s the reason why we can walk without slipping, write with pencils, and drive cars without skidding. Without friction, our everyday activities would be quite chaotic!
When two surfaces come into contact, they have tiny imperfections that interlock with each other. As one surface tries to slide over the other, these imperfections catch on each other, creating resistance. This resistance is what we call friction.
The amount of friction between two surfaces depends on two main factors:
- The Nature of the Surfaces: Rough surfaces have more friction because they have more imperfections that can interlock. Smooth surfaces have less friction.
- The Force Pressing the Surfaces Together: The harder two surfaces are pressed together, the more friction there will be. This is why it’s harder to push a heavy box than a light one.
The force of friction can be calculated using the formula:
\(\displaystyle F_{\text{friction}} = \mu \times F_{\text{normal}} \)
where, (\(\displaystyle\mu\) ) is the coefficient of friction (a number that represents how rough or smooth a surface is) and (\(\displaystyle F_{\text{normal}} \)) is the normal force (the force pressing the two surfaces together).
Friction is a crucial force that allows us to perform everyday tasks. It can be helpful, like when it prevents us from slipping, or a nuisance, like when it causes wear and tear on machine parts.
Types of Friction Force
Friction can be categorized into three main types based on the state of motion:
Static Friction
The frictional force that prevents two surfaces from sliding past each other when a force is applied. It acts up to a certain limit, known as the maximum static friction. It’s the reason why objects don’t move until a certain amount of force is applied.

Imagine you’re trying to push a heavy piece of furniture across the room. You push with all your might, but it doesn’t budge until you’ve applied enough force. This resistance you feel before the furniture starts to move is due to static friction.
Static friction arises because of the microscopic contact points between two surfaces. These contact points create a force that must be overcome to start moving the object. The strength of static friction depends on the types of surfaces involved and how much they are pressed together.
The Laws of Static Friction:
- Independent of Surface Area: The maximum static frictional force is not dependent on the area of contact between the two surfaces.
- Proportional to Normal Force: The maximum static frictional force is directly proportional to the normal force—the force pressing the two surfaces together.
- Self-Adjusting: Static friction adjusts up to a certain maximum value to exactly balance the applied force, preventing motion.
The maximum value of static friction, just before the object starts to slide, is known as limiting friction. If the applied force exceeds this value, the object will begin to move, and static friction no longer applies.
The force of static friction can be calculated using the formula:
\(\displaystyle F_{\text{static}} = \mu_{\text{static}} \times F_{\text{normal}} \)
where (\(\displaystyle \mu_{\text{static}}\) ) is the coefficient of static friction, and (\(\displaystyle F_{\text{normal}} \)) is the normal force.
Static friction is the force that resists the initial movement of two surfaces that are in contact. It’s what keeps a book from sliding off a tilted desk or a car from sliding down a hill when parked. To derive the formula, we need to understand two key forces:
- Normal Force (FN): This is the force exerted by a surface perpendicular to the object resting on it. For an object on a flat surface, it’s equal to the weight of the object due to gravity.
- Frictional Force (Ff): This is the force that resists the motion of the object. For static friction, it’s the force that needs to be overcome to start moving the object.
The coefficient of static friction (μs) is a dimensionless number that represents the amount of friction between two surfaces. It varies depending on the materials and is determined experimentally.
The maximum static frictional force (\(\displaystyle F_{s_{\text{max}}} \)) that can act on an object before it starts moving is directly proportional to the normal force:
\(\displaystyle F_{s_{\text{max}}} = \mu_s \times F_N \)
We know that the static frictional force is proportional to the normal force:
\(\displaystyle F_{s_{\text{max}}} \propto F_N \)
To convert the proportionality into an equation, we introduce the coefficient of static friction (μs):
\(\displaystyle F_{s_{\text{max}}} = \mu_s \times F_N \)
This equation tells us that the maximum static frictional force is equal to the coefficient of static friction multiplied by the normal force.
To find the maximum static frictional force for a given situation, you multiply the coefficient of static friction for the two surfaces by the normal force acting on the object.
Example: If a box is resting on a flat surface the coefficient of static friction between the box and the surface is 0.5, and the weight of the box (and thus the normal force) is 10 N, the maximum static frictional force would be:
\(\displaystyle F_{s_{\text{max}}} = 0.5 \times 10 \, \text{N} = 5 \, \text{N} \)
This means you would need to apply a force greater than 5 N to start moving the box. The formula for static friction is derived from the direct proportionality between the maximum static frictional force and the normal force, with the coefficient of static friction as the constant of proportionality.
Examples of Static Friction:
- A book resting on a desk.
- A car parked on a slope.
- A person standing still on the ground.
Kinetic Friction
Once the static friction threshold is overcome, kinetic friction comes into play, allowing the surfaces to slide relative to each other but still opposing the motion.
When you slide a book across a table or when a hockey puck glides over ice, there’s a force working against the motion. This force is known as kinetic friction.
Imagine you’re trying to move a heavy piece of furniture, like a cabinet, across a wooden floor. Instead of directly sliding the cabinet, you’ve attached wheels to its base to make it easier to move.
As you apply a horizontal force to push the cabinet, the wheels roll smoothly along the surface of the floor. However, you might still feel some resistance, albeit less than before. This resistance is due to kinetic friction, even though the cabinet is rolling on wheels.
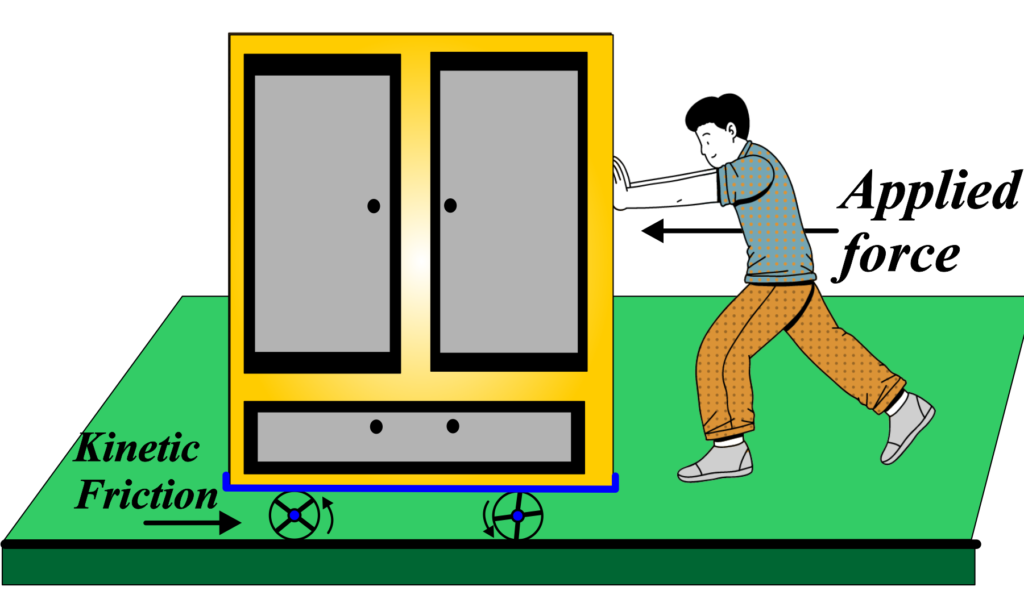
Kinetic friction occurs between the wheels of the cabinet and the surface of the floor. As the wheels roll, there is still some contact between their surfaces and the floor. Tiny irregularities on both surfaces come into contact, creating friction that opposes the motion of the cabinet.
Even though the wheels reduce the amount of friction compared to sliding the cabinet directly, there is still some resistance that needs to be overcome. This frictional force depends on factors like the smoothness of the floor, the weight of the cabinet, and the condition of the wheels.
To minimize kinetic friction and move the cabinet more easily, you might need to exert less force compared to sliding the cabinet without wheels. Additionally, using wheels with ball bearings or lubricating the wheels can further reduce friction, making it even easier to move the furniture.
Kinetic friction is the force that acts between moving surfaces. When an object slides over another, kinetic friction acts in the opposite direction to the movement. The magnitude of this force depends on the nature of the surfaces in contact and how much they are pressed together.
At the microscopic level, surfaces are not as smooth as they appear. They have tiny hills and valleys that interact when one surface moves over another. These interactions create the force of kinetic friction. It’s a force that resists motion, trying to slow down or stop the moving object.
The force of kinetic friction (Fk) can be calculated using the coefficient of kinetic friction (μk) and the normal force (N) acting on the body:
\(\displaystyle F_k = \mu_k \times N \)
The coefficient of kinetic friction is a unitless number that represents the frictional properties of the two surfaces in contact. The normal force is the force exerted by a surface perpendicular to the object resting on it.
Factors Affecting Kinetic Friction
- Surface Material: Different materials have different coefficients of kinetic friction.
- Surface Smoothness: Smoother surfaces tend to have lower kinetic friction.
- Normal Force: The greater the force pressing the surfaces together, the greater the kinetic friction.
It’s important to note that kinetic friction is usually less than static friction, which is the force that needs to be overcome to start moving an object at rest. Once an object is in motion, it’s easier to keep it moving due to the lower kinetic friction.
Examples of Kinetic Friction:
- A sled sliding down a snowy hill.
- A car braking on a road.
- A person sliding furniture across a floor.
Rolling Friction
Rolling Friction occurs when an object rolls over a surface. It is generally less than static or kinetic friction and is the reason why wheels are so effective in transportation systems.
Imagine you’re playing with a toy car. You give it a push, and off it goes, but after a while, it comes to a stop. The force that gradually slows down the rolling toy car is called rolling friction.
Rolling friction is the force that opposes the motion of a body rolling over a surface. It’s much weaker than static or kinetic friction, which is why wheels and ball bearings are so effective in reducing the effort needed to move objects.
When an object rolls, its surface deforms slightly at the point of contact with the ground. The ground also deforms a bit. These deformations cause resistance to the rolling motion. The energy needed to overcome this resistance and keep the object rolling is what we experience as rolling friction.
Factors Affecting Rolling Friction
- Surface Material: The type of material the rolling object and the surface are made of can affect rolling friction.
- Surface Smoothness: Smoother surfaces tend to have lower rolling friction.
- Load: The weight of the rolling object can influence the amount of rolling friction.
- Diameter of the Rolling Object: Larger diameters can reduce rolling friction because they spread the load over a larger area.
The force of rolling friction can be calculated using the formula:
\(\displaystyle F_r = \mu_r \times \frac{W}{r} \)
where (Fr) is the force of rolling friction, (μr) is the coefficient of rolling friction, (W) is the weight of the rolling body, and (r) is the radius of the rolling object.
Rolling friction is the force that opposes the motion of an object rolling over a surface. It’s less than static or kinetic friction and is crucial for understanding how wheels and ball bearings work.
When an object rolls over a surface, the point of contact deforms slightly due to the weight of the object. This deformation causes resistance to the rolling motion, which we call rolling friction.
- Normal Force (N): This is the force exerted by the surface perpendicular to the rolling object. It’s equal to the weight of the object if the surface is horizontal.
- Rolling Friction Force (Fr): This is the force that opposes the rolling motion.
The coefficient of rolling friction (μr) is a dimensionless number that represents the amount of rolling friction between two surfaces. It varies depending on the materials and is determined experimentally. The force of rolling friction can be expressed as:
\(\displaystyle F_r = \mu_r \times \frac{W}{r} \)
where (Fr) is the force of rolling friction, (μr) is the coefficient of rolling friction, (W) is the weight of the rolling body, and (r) is the radius of the rolling object.
We know that the rolling frictional force is proportional to the normal force and inversely proportional to the radius of the rolling object:
\(\displaystyle F_r \propto \frac{N}{r} \)
To convert the proportionality into an equation, we introduce the coefficient of rolling friction (μr):
\(\displaystyle F_r = \mu_r \times \frac{N}{r} \)
Since the normal force is equal to the weight of the object (W) for a horizontal surface, we substitute (N) with (W):
\(\displaystyle F_r = \mu_r \times \frac{W}{r} \)
To find the force of rolling friction for a given situation, you multiply the coefficient of rolling friction for the two surfaces by the weight of the rolling body and divide by the radius of the rolling object.
Example: If a tire weights 100 N, a radius of 0.5 meters, and the coefficient of rolling friction is 0.02, the rolling friction force would be:
\(\displaystyle F_r = 0.02 \times \frac{100 \, \text{N}}{0.5 \, \text{m}} = 4 \, \text{N} \)
Examples of Rolling Friction:
- A basketball rolling to a stop on a court.
- A bicycle slows down when you stop pedaling.
- Luggage wheels drag slightly as you pull them across the airport floor.
Also Read: Uniform Circular Motion
Spring Force
Spring force is a restoring force exerted by a spring when it is compressed or stretched. According to Hooke’s Law, the force is proportional to the displacement from the equilibrium position.
Imagine you have a spring from a pen. If you compress or stretch it, you can feel it pushing back against your hand. This force that the spring exerts to return to its original shape is called the spring force.
Spring force is a restoring force; it always acts to bring the spring back to its equilibrium position. Whether you compress or stretch a spring, it will exert a force in the opposite direction to get back to where it started.
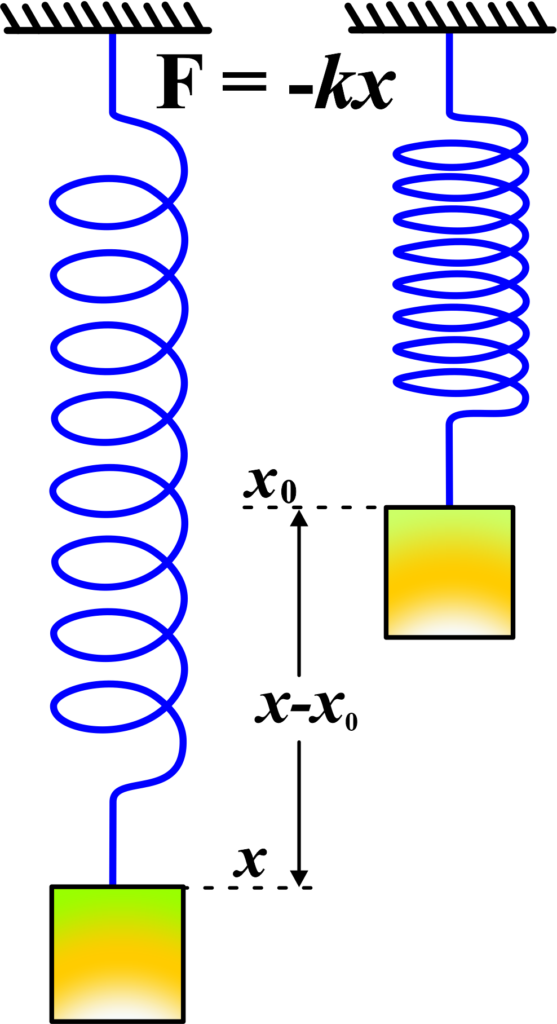
Spring force is based on Hooke’s Law, which states that the force exerted by a spring is directly proportional to the displacement from its original length. The more you stretch or compress it, the greater the force it exerts.
The force of a spring (Fs) can be calculated using Hooke’s Law:
\(\displaystyle F_s = -k \times x \)
Where,
- (Fs) is the spring force,
- (k) is the spring constant (a measure of the spring’s stiffness),
- (x) is the displacement from the spring’s original length,
- The negative sign indicates that the force is in the opposite direction of the displacement.
The spring constant (k) is unique to each spring and depends on the material and dimensions of the spring. It’s measured in Newtons per meter (N/m). A stiffer spring has a higher spring constant.
Examples of Spring Force:
- The suspension system in cars uses springs to absorb shocks.
- Trampolines use spring force to bounce you back up after you jump.
- Pogo sticks use springs to convert your downward force into motion.
Spring force is a fundamental concept in physics that explains how springs behave when they are compressed or stretched.
Tension Force
Tension force is the pulling force transmitted through a string, rope, or cable when forces are applied at the ends. It acts along the length of the object and is directed away from the object, keeping the material taut.
Imagine you’re playing tug-of-war. The rope you’re pulling on is taut, and you can feel it pulling back against you. This force within the rope is what we call tension force.

Tension force is the pulling force transmitted through a string, rope, cable, or any flexible connector when forces act from opposite ends. It’s a force that acts along the length of the medium and pulls equally on the objects it’s connected to.
When you pull on a rope, every part of the rope experiences tension. The rope transmits the force you apply from one end to the other. If you hang a weight from a rope, the tension force is what holds the weight up against gravity.
Characteristics of Tension Force:
- Direction: Tension force always pulls along the line of the rope or cable.
- Transmission: It efficiently transfers force over the distance of the rope or cable.
- Equilibrium: If the rope is stationary, the tension force throughout the rope is constant and balances the forces applied.
The tension force can be calculated using the formula:
\(\displaystyle T = mg + ma \)
- (T) is the tension force,
- (m) is the mass of the object,
- (g) is the acceleration due to gravity (approximately ( 9.8 m/s2 ) on Earth),
- (a) is the acceleration of the object (if any).
Examples of Tension Force:
- A climber hanging from a rope.
- A chandelier suspended from the ceiling by a chain.
- A car is being towed by a tow truck.
Tension force is a fundamental concept in physics that describes the pulling force within ropes, cables, and other flexible connectors.
Normal Force
When you place a book on a table, you know it doesn’t fall through. That’s because there’s a force from the table supporting the book. This force is called the normal force.
The normal force is the force exerted by a surface that supports the weight of an object resting on it. It acts perpendicular (at a right angle) to the surface. The term “normal” in this context means perpendicular.
Imagine you have a box placed on an inclined plane, which means the surface is tilted at an angle. When the box rests on the inclined plane, the force of gravity acts vertically downward, pulling the box toward the center of the Earth.
Now, let’s focus on the forces acting on the box. There are two main forces: the gravitational force pulling the box downward and the normal force exerted by the inclined plane upward, perpendicular to the surface.
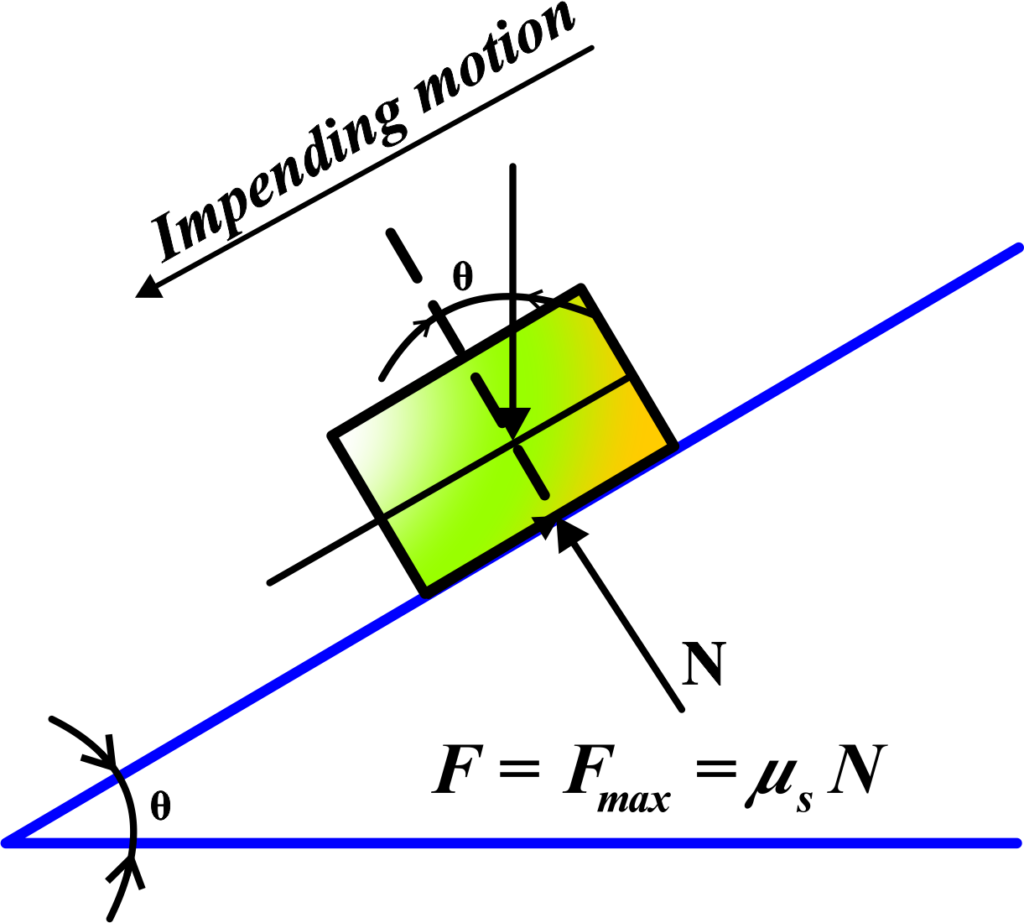
Initially, when the box is stationary on the inclined plane, the normal force counteracts the component of the gravitational force perpendicular to the plane. This prevents the box from sinking into the surface of the inclined plane.
However, if you try to push the box horizontally along the inclined plane, the situation changes.
As you apply a horizontal force to the box, you’re effectively trying to overcome the static frictional force between the box and the inclined plane.
Impeding motion occurs when the force you apply is not sufficient to overcome the maximum static frictional force between the box and the inclined plane. In other words, the normal force increases to match the applied force, resisting the box’s motion along the plane. The box remains stationary until the applied force reaches a critical value, at which point the static frictional force is overcome, and the box starts moving.
The normal force arises because objects are solid and surfaces can’t pass through each other. When an object is placed on a surface, gravity pulls it down. The surface pushes back with a force equal in magnitude but opposite in direction to the gravitational force, preventing the object from falling through.
Characteristics of Normal Force:
- It’s a contact force, meaning it only exists when two surfaces are in contact.
- It acts perpendicular to the surface of contact.
- The magnitude of the normal force is usually equal to the weight of the object when it’s on a horizontal surface.
On a flat surface, the normal force (FN) is equal to the weight of the object (W), which is the mass (m) times the acceleration due to gravity (g):
\(\displaystyle F_N = m \times g \)
If the surface is inclined, the normal force is the component of the object’s weight perpendicular to the surface.
Examples of Normal Force:
- A person standing on the ground feels a normal force equal to their weight pushing up from the floor.
- A book resting on a desk experiences a normal force from the desk that balances its weight.
The normal force is a fundamental concept in physics that explains how surfaces support objects. It’s essential for understanding how objects interact with their environment and is a key force in many mechanics problems.
Drag Force
Drag force is the resistance force caused by the motion of a body through a fluid, such as air or water. It acts opposite to the direction of the oncoming flow velocity and is influenced by the object’s speed, surface area, and the fluid’s density.
Imagine you’re riding a bicycle against the wind. You can feel the air pushing against you, making it harder to pedal. This resistance is known as drag force.
Drag force is the resistance force caused by the motion of a body through a fluid, such as air or water. It acts in the opposite direction to the oncoming flow velocity, which means it opposes the motion of the object moving through the fluid.
As an object moves, it has to push the fluid molecules out of the way. The interaction between the object’s surface and the fluid molecules creates drag force. This force is dependent on several factors, including the speed of the object, the viscosity of the fluid, and the shape of the object.
- Velocity: The faster the object moves, the greater the drag force.
- Cross-sectional Area: A larger area facing the flow increases the drag force.
- Shape: Streamlined shapes reduce drag force, which is why sports cars and airplanes are designed to be aerodynamic.
- Fluid Density: Denser fluids, like water, create more drag than less dense fluids, like air.
- Surface Texture: Smooth surfaces reduce drag compared to rough surfaces.
The drag force (Fd) can be calculated using the equation:
\(\displaystyle F_d = \frac{1}{2} C_d \rho v^2 A \)
- (Cd) is the drag coefficient,
- (ρ) is the fluid density,
- (v) is the velocity of the object,
- (A) is the cross-sectional area.
Examples:
- Parachutes use drag force to slow down descent.
- Swimmers experience drag force as they move through the water.
- Cars are designed with aerodynamics in mind to reduce drag force and improve fuel efficiency.
Drag force is a crucial concept in physics that explains how objects interact with fluids they move through.
Pseudo Force
Pseudo force, or fictitious force, arises when observing motion from a non-inertial (accelerating) frame of reference. It appears to act on objects within the accelerating frame but does not result from any physical interaction. An example is the force you feel pushing you back into your seat when a car accelerates.
Imagine you’re sitting in a car that suddenly starts accelerating. You feel like you’re being pushed back into your seat. This sensation is due to a pseudo force.
Pseudo force is an apparent force that you feel when you’re in a non-inertial frame of reference, which means the frame is accelerating. It’s not a real force caused by an interaction between objects. Instead, it’s a result of the acceleration of the frame itself.
Pseudo force comes into play when you’re observing motion from a reference frame that is accelerating. For example, if you’re in a car that’s speeding up, you feel like you’re being pushed back, even though no physical force is acting on you in that direction.
Characteristics of Pseudo Force:
- It’s felt by observers within an accelerating system.
- It’s proportional to the mass of the object and the acceleration of the system.
- It appears to act in the opposite direction of the system’s acceleration².
Examples of Pseudo Force:
- Feeling pushed back in a car that accelerates forward.
- Feeling pushed to the side in a turning vehicle.
- Objects slide to the rear of a plane when it takes off.
The magnitude of the pseudo force (Fp) can be calculated using the formula:
\(\displaystyle F_p = -m \times a \)
- (m) is the mass of the object,
- (a) is the acceleration of the reference frame,
- The negative sign indicates that the pseudo force acts in the opposite direction to the acceleration.
Pseudo force is a concept that helps us understand the effects of acceleration from within a non-inertial frame of reference. It’s not a real force like gravity or friction, but it’s a useful idea for explaining why objects seem to move when viewed from an accelerating system, such as a car or a rotating planet.
Solved Examples
Problem 1: A block of mass (5 kg) is placed on an inclined plane making an angle of (30∘) with the horizontal. The coefficient of static friction between the block and the plane is (0.4). Calculate the maximum static frictional force and determine whether the block will slide down the plane.
Solution: The maximum static frictional force (fs) is given by:
\(\displaystyle f_s = \mu_s N \)
Where (N) is the normal force. The normal force is:
\(\displaystyle N = mg \cos \theta \)
Where: m = 5 kg; g = 9.8 m/s2 ; θ = 30∘
\(\displaystyle N = 5 \times 9.8 \times \cos 30^\circ \)
\(\displaystyle N = 5 \times 9.8 \times \frac{\sqrt{3}}{2} \)
\(\displaystyle N = 5 \times 9.8 \times 0.866 \)
\(\displaystyle N \approx 42.35 \, \text{N} \)
The maximum static frictional force:
\(\displaystyle f_s = 0.4 \times 42.35 \approx 16.94 \, \text{N} \)
The component of gravitational force parallel to the incline is:
\(\displaystyle F_{\parallel} = mg \sin \theta \)
\(\displaystyle F_{\parallel} = 5 \times 9.8 \times \sin 30^\circ \)
\(\displaystyle F_{\parallel} = 5 \times 9.8 \times 0.5 \)
\(\displaystyle F_{\parallel} = 24.5 \, \text{N} \)
Since (\(\displaystyle F_{\parallel} > f_s \)), the block will slide down the plane.
Problem 2: A sled of mass (10 kg) is moving on a horizontal surface with a coefficient of kinetic friction (µk = 0.3 ). If the sled is initially moving at (5 m/s), calculate the distance it will travel before coming to rest.
Solution: The kinetic frictional force (fk) is given by:
\(\displaystyle f_k = \mu_k N \)
Where (N) is the normal force. On a horizontal surface:
N = mg
So,
\(\displaystyle f_k = \mu_k mg = 0.3 \times 10 \times 9.8 = 29.4 \, \text{N} \)
The work done by the kinetic frictional force to stop the sled is equal to the initial kinetic energy of the sled:
\(\displaystyle W = f_k \cdot d \)
\(\displaystyle \frac{1}{2} m v^2 = f_k \cdot d \)
\(\displaystyle \frac{1}{2} \times 10 \times 5^2 = 29.4 \times d \)
$ 125 = 29.4 \times d $
\(\displaystyle d = \frac{125}{29.4} \approx 4.25 \, \text{m} \)
The sled will travel approximately (4.25 m) before coming to rest.
Problem 3: A car of mass (1500 kg) is moving at a speed of (20 m/s). The coefficient of rolling friction between the tires and the road is (0.015). Calculate the distance the car will travel before coming to a stop due to rolling friction.
Solution: The rolling frictional force (fr) is given by:
\(\displaystyle f_r = \mu_r N \)
Where (N) is the normal force:
N = mg
So,
\(\displaystyle f_r = \mu_r mg = 0.015 \times 1500 \times 9.8 = 220.5 \, \text{N} \)
The work done by the rolling frictional force to stop the car is equal to the initial kinetic energy of the car:
\(\displaystyle W = f_r \cdot d \)
\(\displaystyle \frac{1}{2} m v^2 = f_r \cdot d \)
\(\displaystyle \frac{1}{2} \times 1500 \times 20^2 = 220.5 \times d \)
\(\displaystyle 300000 = 220.5 \times d \)
\(\displaystyle d = \frac{300000}{220.5} \approx 1360 \, \text{m} \)
The car will travel approximately (1360 m) before coming to a stop due to rolling friction.
Problem 4: A spring has a spring constant (k = 200 N/m). A mass of (2 kg) is attached to the spring and stretched (0.1 m) from its equilibrium position. Calculate the force exerted by the spring and the potential energy stored in the spring.
Solution: The force exerted by the spring (Fs) is given by Hooke’s law:
\(\displaystyle F_s = -kx \)
Where:
- (k = 200 N/m)
- (x = 0.1 m)
\(\displaystyle F_s = -200 \times 0.1 = -20 \, \text{N} \)
The potential energy (U) stored in the spring is:
\(\displaystyle U = \frac{1}{2} k x^2 \)
\(\displaystyle U = \frac{1}{2} \times 200 \times (0.1)^2 \)
\(\displaystyle U = \frac{1}{2} \times 200 \times 0.01 \)
U = 1 J
The force exerted by the spring is (-20 N) and the potential energy stored in the spring is (1J).
Problem 5: Two blocks of masses (3 kg) and (2 kg) are connected by a light string and are pulled by a force of (30 N) on a frictionless surface. Calculate the tension in the string connecting the two blocks.
Solution: The total mass (\(\displaystyle m_{\text{total}} \)) is:
\(\displaystyle m_{\text{total}} = 3 + 2 = 5 \, \text{kg} \)
The acceleration (a) of the system is:
\(\displaystyle F = m_{\text{total}} a \)
30 = 5a
\(\displaystyle a = \frac{30}{5} = 6 \, \text{m/s}^2 \)
The tension (T) in the string between the two blocks is responsible for accelerating the (2 kg) block:
\(\displaystyle T = m_2 a \)
\(\displaystyle T = 2 \times 6 = 12 \, \text{N} \)
The tension in the string connecting the two blocks is (12 N).
FAQs
What are contact forces, and can you give examples?
Contact forces are forces that act between two objects that are physically touching each other. Examples include frictional forces, where two surfaces rub against each other, normal forces, which support the weight of an object on a surface, and tension forces, such as those in a stretched rope or cable.
How do gravitational forces influence objects on Earth and in space?
Gravitational forces are attractive forces between objects with mass. On Earth, gravitational forces pull objects towards the center of the planet, causing them to accelerate downward. In space, gravitational forces between celestial bodies, like planets and stars, determine their orbits and interactions.
What are the fundamental differences between tension and compression forces?
Tension forces act to stretch or pull apart objects, like in a taut rope or a stretched spring, while compression forces act to push or squeeze objects together, like in a compressed spring or a loaded column. Both tension and compression forces can occur in structures like bridges and buildings.
How do air resistance and drag forces affect moving objects?
Air resistance, also known as drag force, opposes the motion of objects moving through a fluid medium like air or water. It depends on factors such as the object’s speed, shape, and surface area. Air resistance can slow down moving objects and affect their trajectories, particularly in sports like cycling and skydiving.
Are there forces at play in objects at rest?
Yes, even objects at rest experience forces. For example, an object sitting on a surface experiences a gravitational force pulling it downward and a normal force from the surface pushing it upward. When these forces are balanced, the object remains at rest due to Newton’s first law of motion.
How do spring forces contribute to the behavior of elastic materials?
Spring forces, also known as restoring forces, occur in elastic materials like springs and rubber bands when they are stretched or compressed. These forces act to return the material to its original shape and size when the deforming force is removed. Spring forces are central to the behavior of elastic materials in various engineering applications.