The idea of power as we understand it in physics today has roots that go back to ancient civilizations. However, it wasn’t until the scientific developments during the Renaissance that the concept began to take a more defined shape.
The ancient Greeks had notions of power related to simple machines, but these ideas were not fully developed into scientific terms. Aristotle used the term “energhéia” to describe the idea of potentiality becoming actuality.
Around 60 AD, Hero of Alexandria described the concept of work done using simple machines like pulleys, hinting at the relationship between force, distance, and speed.
In the 17th century, Galileo Galilei and René Descartes laid the groundwork for the concept of power without explicitly using the term. They discussed the impossibility of certain machines and the conservation of motion.
Gottfried Wilhelm Leibniz introduced the term “vis viva” or “living force,” which is the precursor to our modern concept of kinetic energy. He argued that this living force was conserved and was related to mass and the square of velocity.
The term “power” became more scientifically relevant during the Industrial Revolution. James Watt, famous for improving the steam engine, needed a way to compare the output of his engines to the work done by horses, which led to the development of the concept of horsepower.
The debates and discoveries in the 18th and 19th centuries about energy conservation, where scientists like Émilie du Châtelet contributed, eventually solidified the concept of power as the rate of energy transfer.
What is Power?
Power is the rate at which work is done or energy is transferred. In simpler terms, it tells us how fast something is using energy or doing work.
In physics, power is defined as the rate at which work is done or energy is transferred. It’s essentially a measure of how quickly something is happening. When we talk about power in a physical sense, we’re interested in how fast energy is being used or how fast work is being completed.
Imagine you and your friend are both climbing stairs. You reach the top in 1 minute, but your friend takes 2 minutes to do the same. Even though you both did the same amount of work (climbing the same height), you did it faster. In physics terms, you had more power.
Here’s another way to think about it: Imagine you have a light bulb connected to a battery. When you switch on the light bulb, electrical energy from the battery is converted into light and heat energy. The rate at which this conversion occurs is the power of the light bulb.
Mathematically, power is defined as the amount of energy transferred or converted per unit of time. In the case of our light bulb, the power is the rate at which electrical energy is converted into light and heat.
Let’s say the light bulb has a power rating of 60 watts (60 W). This means that the light bulb converts 60 joules of electrical energy into light and heat energy every second.
The higher the power rating of the light bulb, the brighter it will shine, and the more energy it will consume.
So, power is all about speed—the speed of doing work or using energy. It’s a crucial concept because it helps us understand and compare how efficient or effective different processes or machines are at using energy.
Remember, power is not the same as energy. Energy is like the total amount of effort you have to spend, while power is how fast you spend that effort.
Power Formula: Power is all about how fast work is done or how energy is used. The basic formula for power is quite straightforward:
\(\displaystyle P = \frac{W}{t} \)
Here, (P) stands for power, (W) for work done, and (t) for time. This formula tells us that power is the work done divided by the time it takes to do that work.
Units and Dimensional Formula of Power:
The unit of power in the International System of Units (SI) is the watt (symbol: W). One watt is defined as one joule of energy transferred or work done per one second. In other words, if one joule of work is done in one second, the power associated with this process is one watt.
Dimensional Formula of Power:
The dimensional formula is a way to represent the units of a physical quantity in terms of the basic dimensions (Mass, Length, Time, etc.). For power, the dimensional formula is:
\(\displaystyle [P] = [M^1L^2T^{-3}] \)
This formula tells us that power has dimensions of mass to the first power, length squared, and time to the negative third power. Here’s what each symbol represents:
So, when we say the dimensional formula of power is ( [M1L2T-3] ), we’re saying that power is directly related to mass and the square of length, and inversely related to the cube of time.
Power is defined as the rate at which work is done. The formula for power (P ) is given by the work done (W) divided by the time (t) it takes to do the work. So, we have:
\(\displaystyle P = \frac{W}{t} \)
Work (W): Work is defined as force (F) multiplied by displacement (d). The dimensional formula for force is ( [MLT-2] ) (mass times acceleration), and displacement is simply a measure of length, so its dimensional formula is ([L]). Therefore, the dimensional formula for work is:
\(\displaystyle [W] = [F][d] = [MLT^{-2}][L] = [ML^2T^{-2}] \)
Time (t): Time is a fundamental quantity, and its dimension is ([T]).
Now, we can substitute the dimensions of work and time into the power formula:
\(\displaystyle [P] = \frac{[W]}{[T]} = \frac{[ML^2T^{-2}]}{[T]} \)
When we divide the dimensions of work by the dimensions of time, we get:
\(\displaystyle [P] = [ML^2T^{-3}] \)
So, the dimensional formula for power is ([ML2T-3]). This tells us that power is a physical quantity that depends on mass, length, and time.
Understanding the dimensional formula is important because it helps us check the correctness of physical equations and convert units from one system to another. It’s a fundamental part of understanding how different physical quantities are related to each other.
What is Horsepower?
Horsepower (hp) is a unit of power commonly used in the context of engines and machinery, particularly in the automotive and mechanical engineering industries. It measures the rate at which work is done or energy is transferred, specifically in terms of the amount of mechanical power required to lift 550 pounds (approximately 250 kilograms) by one foot (about 0.3048 meters) in one second.
The concept of horsepower was popularized by James Watt, an 18th-century Scottish engineer who sought a way to compare the power output of his steam engines to the work done by draft horses. He determined that a strong horse could lift a weight of 550 pounds by one foot in one second, and he used this as a standard to define one horsepower.
Mathematically, one horsepower is equivalent to:
\(\displaystyle 1 \, \text{horsepower} = \frac{550 \, \text{ft-lbf}}{s} \)
- 1 hp represents one horsepower,
- 550 ft-lbf/s represents the work done by lifting 550 pounds by one foot in one second.
Horsepower is commonly used to specify the power output of engines, such as those found in cars, trucks, boats, and other machinery. For example, a car’s engine might be rated at 200 horsepower, indicating its ability to perform work or produce energy at a rate equivalent to 200 times the work done by a horse.
The watt (W) is the standard unit of power in the International System of Units (SI). It is defined as one joule per second, where a joule is the unit of energy.
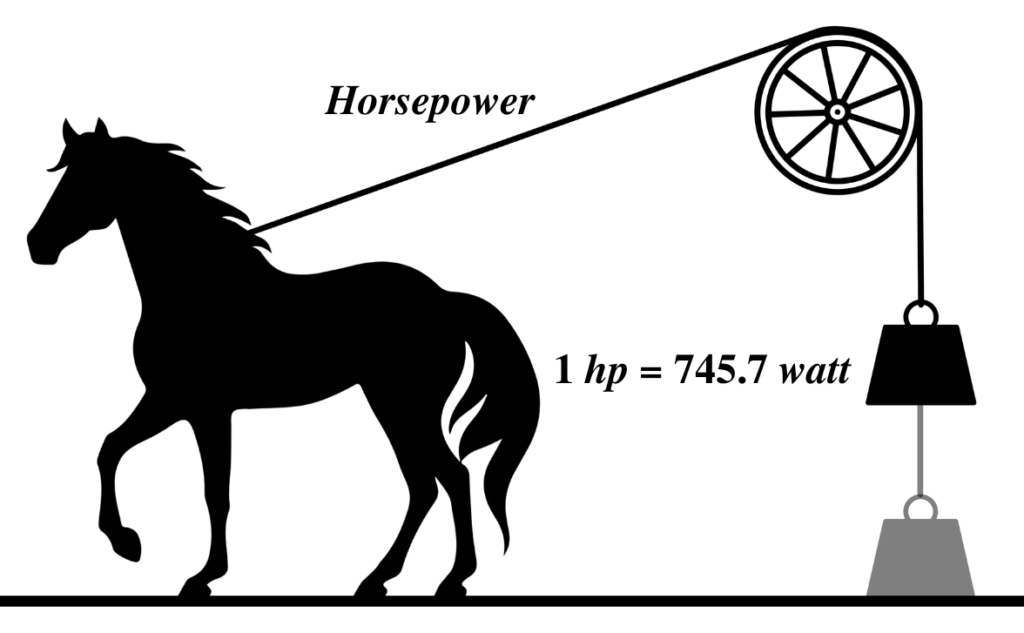
To establish the relationship between horsepower and watts, we need to consider the definition of one horsepower, which is based on the work done by a horse lifting a weight of 550 pounds by one foot in one second.
Now, to convert horsepower to watts, we can use the following conversion factor:
\(\displaystyle 1 \, \text{horsepower} = 550 \, \text{ft-lbf/s} \)
Since 1 foot-pound (ft-lbf) is equivalent to approximately 1.35582 joules, we can convert the horsepower to watts as follows:
\(\displaystyle 1 \, \text{horsepower} = 550 \times 1.35582 \, \text{W} \)
\(\displaystyle 1 \, \text{horsepower} \approx 745.7 \, \text{W} \)
Therefore, 1 horsepower is approximately equal to 745.7 watts. This conversion factor allows us to relate power measurements in horsepower to those in watts.
In summary, horsepower is a historical unit of power that has stuck around because it’s a practical way to measure and compare the power output of various engines and motors. It’s a bridge between the past and present, showing us just how far technology has come since the days of using actual horsepower.
Average Power
Average power is a fundamental concept related to how quickly work is done or energy is converted. It’s like looking at the overall performance of an activity over a period of time. Here’s what you need to know:
Definition: Average power is the total energy consumed divided by the total time taken. In simpler terms, it represents the average amount of work done or energy converted per unit of time.
Mathematically, average power (\(\displaystyle P_{\text{avg}}\)) is calculated using the following equation:
\(\displaystyle P_{\text{avg}} = \frac{\text{Total Work Done (W)}}{\text{Time (t)}} \)
The standard metric unit for power is the watt (W). It’s defined as joules per second (J/s). Sometimes, you might come across the term horsepower (hp). One horsepower is approximately equal to 745.7 watts.
Example: Let’s consider an example with light bulbs: Suppose we have two 60-watt bulbs: Bulb A is switched on for 24 hours. Bulb B is turned on for only 12 hours. For the first 12 hours, both bulbs are ON, so the total power is (60 + 60 = 120) watts.
Energy consumed during this time: \(\displaystyle 120 \times 12 = 1.44\) kilowatt-hours (kWh).
For the next 12 hours, only bulb A remains ON, so the power is (60) watts.
Energy consumed during this time: \(\displaystyle 60 \times 12 = 0.72\) kWh.
To find the average power, we add up the total energy consumed and divide by the total time taken:
\(\displaystyle \text{Average Power} = \frac{1.44 + 0.72}{24} = 0.092 \text{ kW} \)
Power tells us how quickly energy is being used. It determines how fast work can be done. Remember, average power helps us understand efficiency, whether it’s in light bulbs, engines, or even ourselves as machines.
Electric Power
Definition: Electric power (P) measures the rate at which electrical energy is transferred by an electric circuit per unit of time. In simpler terms, it tells us how quickly energy is being used or work is being done in an electrical system.
The standard unit of power is the watt (W), which is equivalent to one joule per second. The formula for electric power is:
\(\displaystyle P = VI \)
Alternate Expressions:
Power can also be expressed using Ohm’s law: Ohm’s Law states that the current (I) flowing through a conductor between two points is directly proportional to the voltage (V) across the two points and inversely proportional to the resistance (R) of the conductor. The law is usually expressed as:
\(\displaystyle V = IR \)
We can substitute (I) from Ohm’s Law \(\displaystyle (I = \frac{V}{R})\) into the power formula:
\(\displaystyle P = V \left(\frac{V}{R}\right) \)
Simplifying this, we get:
\(\displaystyle P = \frac{V^2}{R} \)
This is the power formula in terms of voltage and resistance.
Expressing Power in Terms of Current and Resistance:
Alternatively, we can express current (I) from Ohm’s Law (V = IR) and substitute it into the power formula:
\(\displaystyle P = (IR)I \)
Simplifying this, we get:
\(\displaystyle P = I^2R \)
This is the power formula in terms of current and resistance.
\(\displaystyle P = \frac{V^2}{R} \): This tells us that power is proportional to the square of the voltage across a resistor and inversely proportional to the resistance. If the voltage is doubled, the power increases by four times, assuming the resistance stays the same.
\(\displaystyle P = I^2R \): This indicates that power is proportional to the square of the current through a resistor and directly proportional to the resistance. If the current is doubled, the power increases by four times, provided the resistance remains constant.
- Voltage and Power: Higher voltage across a resistor leads to higher power consumption.
- Current and Power: Higher current through a resistor also leads to higher power consumption.
- Resistance and Power: Higher resistance with the same voltage leads to lower power consumption, but higher resistance with the same current leads to higher power consumption.
Energy Consumption: Since power is the rate of energy consumption, we can calculate energy directly using:
\(\displaystyle P = \frac{E}{t} \)
Remember, electric power is all about how fast energy is being used in electrical circuits.
Instantaneous Power
Definition: Instantaneous power is the amount of power measured at a specific instant in time. It tells us how quickly energy is being used or work is being done at that particular moment.
The formula for instantaneous power (p) is based on the product of instantaneous voltage (v) and instantaneous current (i) through an element:
\(\displaystyle p = v \times i \)
Instantaneous power is measured in watts (W).
How Does Instantaneous Power Vary?
Pure Resistive Circuit: In a pure resistive circuit (like a simple resistor), the instantaneous voltage and current vary sinusoidally with time. The expression for instantaneous power in a pure resistive circuit is:
\(\displaystyle p = V_m I_m \cos(2\omega t) \)
- (Vm) is the maximum voltage (amplitude),
- (Im) is the maximum current (amplitude),
- (ω) is the angular frequency (related to the frequency of the AC source),
- (t) is time.
Pure Inductive Circuit: In a pure inductive circuit (with only an inductor), the instantaneous voltage and current are out of phase by 90 degrees. The expression for instantaneous power in a pure inductive circuit is:
\(\displaystyle p = -V_m I_m \sin(2\omega t) \)
Pure Capacitive Circuit: In a pure capacitive circuit (with only a capacitor), the instantaneous voltage and current are also out of phase by 90 degrees. The expression for instantaneous power in a pure capacitive circuit is the same as in the inductive case:
\(\displaystyle p = -V_m I_m \sin(2\omega t) \)
Instantaneous power varies with time due to the changing voltage and current. It can be positive or negative, depending on the phase relationship between voltage and current. Understanding instantaneous power helps us analyze AC circuits and optimize energy usage.
Mechanical Power
Mechanical power is the product of a force applied to an object and the object’s velocity, or the product of torque on a shaft and the shaft’s angular velocity.
Definition: Mechanical power is the rate at which work is done in any mechanical system. It’s how quickly energy is being used to move something or cause a change in a physical system.
The formula for mechanical power (P) is the product of force (F) and velocity (v):
\(\displaystyle P = F \cdot v \)
The SI unit of mechanical power is the watt (W), which is equivalent to one joule per second (J/s).
Mechanical power combines both the force applied to an object and the movement of that object. It accounts for the distance an object travels over time due to the force.
Imagine pushing a box across the floor. If you apply force to move the box at a constant speed, you’re doing work on the box. The faster you move the box (higher velocity), the more power you’re exerting.
Consumption of Energy and Power
Energy Consumption: This refers to the total amount of energy used by a device or system over a certain period of time. It’s like the “fuel” consumed by the system to perform its functions.
Energy Consumption is measured in kilowatt-hours (kWh) or joules (J). It represents the total energy used over a period, such as a day, month, or year. Energy consumption is what utility companies measure to calculate your energy bills. The more energy you consume, the higher your bill.
For example, if a light bulb is rated at 100 watts and it’s used for 10 hours, the energy consumption would be 1 kWh (because 100 watts x 10 hours = 1000 watt-hours, or 1 kWh).
Power Consumption: Power consumption, on the other hand, is the rate at which this energy is used. It’s like the “speed” at which the system uses its fuel.
Power consumption is measured in watts (W) or kilowatts (kW). Indicates the instantaneous use of energy at any given moment. Power consumption helps us understand the efficiency of devices. A device that has a lower power consumption for the same output is considered more efficient.
Efficiency can be improved by reducing power consumption or getting more output for the same amount of energy consumed. For instance, the same 100-watt light bulb, when turned on, consumes power at a rate of 100 watts.
Difference Between Power and Energy
Power is the rate at which energy is used or work is done, while energy is the capacity to do work. Power is measured in watts, and energy is measured in joules.
| Aspect | Power | Energy |
|---|---|---|
| Definition | Power is the rate at which work is done or energy is transferred. | Energy is the capacity to do work or the amount of work done. |
| Units | The SI unit of power is the watt (W), which is joules per second (J/s). | The SI unit of energy is the joule (J). |
| Symbol | Power is denoted by the symbol (P). | Energy is denoted by the symbol (E). |
| Formula | \(\displaystyle P = \frac{W}{t} \) | \(\displaystyle E = P \times t \) |
| Measurement | Power measures how quickly energy is used or work is done. | Energy measures the total amount of work done. |
| Conversion | Power cannot be converted from one form to another. | Energy can be converted from one form to another. |
| Storage | Power cannot be stored. | Energy can be stored and used later. |
| Types | Examples include electric power, mechanical power, and thermal power. | Examples include kinetic energy, potential energy, and thermal energy. |
| Change | Power does not change form but indicates the rate of energy transfer. | Energy changes form during processes like doing work or heating an object. |
This table summarizes the key differences between power and energy, two fundamental concepts in physics that are often used interchangeably but have distinct meanings and implications.
Solved Examples
Example 1: A machine lifts a mass of (200 kg) to a height of (10 m) in (20 s). Calculate the power developed by the machine.
Solution: Given; Mass lifted, (m = 200 kg); Height lifted, (h = 10 m); Time taken, (t = 20 s); Acceleration due to gravity, (g = 9.8 m/s2)
The work done by the machine is equal to the gravitational potential energy gained by the mass:
\(\displaystyle W = mgh \)
\(\displaystyle W = 200 \times 9.8 \times 10 \)
\(\displaystyle W = 19600 \, \text{J} \)
Power is defined as the rate at which work is done or energy is transferred:
\(\displaystyle \text{Power} = \frac{\text{Work done}}{\text{Time taken}} \)
\(\displaystyle \text{Power} = \frac{19600}{20} \)
\(\displaystyle \text{Power} = 980 \, \text{W} \)
Therefore, the power developed by the machine is (980W).
Example 2: A cyclist applies a force of (200 N) to ride his bicycle at a constant speed of (5 m/s) for (10 s). Calculate the average power developed by the cyclist.
Solution: Given; A force applied by the cyclist, (F = 200 N); Speed of the bicycle, (v = 5 m/s); Time taken, (t = 10 s).
The work done by the cyclist is equal to the product of the force and the distance traveled:
\(\displaystyle W = F \times d \)
Since the speed is constant, distance (d) can be calculated as:
\(\displaystyle d = v \times t \)
\(\displaystyle d = 5 \times 10 \)
\(\displaystyle d = 50 \, \text{m} \)
Substitute the value of (d) into the work equation:
\(\displaystyle W = 200 \times 50 \)
\(\displaystyle W = 10000 \, \text{J} \)
Average power is given by:
\(\displaystyle \text{Average Power} = \frac{\text{Work done}}{\text{Time taken}} \)
\(\displaystyle \text{Average Power} = \frac{10000}{10} \)
\(\displaystyle \text{Average Power} = 1000 \, \text{W} \)
Therefore, the average power developed by the cyclist is (1000 W).
Example 3: A car with a mass of (1500 kg) accelerates from rest to a speed of (20 m/s) in (10 s). Calculate the instantaneous power developed by the engine when the car reaches a speed of (15 m/s).
Solution: Given; Mass of the car, (m = 1500 kg); Initial speed, (vi = 0 m/s); Final speed, (vf = 15 m/s); Time taken, (t = 10 s)
Acceleration can be calculated using the formula:
\(\displaystyle a = \frac{\Delta v}{\Delta t} \)
\(\displaystyle a = \frac{v_f – v_i}{t} \)
\(\displaystyle a = \frac{15 – 0}{10} \)
\(\displaystyle a = 1.5 \, \text{m/s}^2 \)
The force required to accelerate the car can be calculated using Newton’s second law:
\(\displaystyle F = ma \)
\(\displaystyle F = 1500 \times 1.5 \)
\(\displaystyle F = 2250 \, \text{N} \)
Instantaneous power is given by the product of force and velocity:
\(\displaystyle \text{Instantaneous Power} = F \times v \)
\(\displaystyle \text{Instantaneous Power} = 2250 \times 15 \)
\(\displaystyle \text{Instantaneous Power} = 33750 \, \text{W} \)
Therefore, the instantaneous power developed by the engine when the car reaches a speed of (15 m/s) is (33750 W).
Example 4: A resistor has a voltage drop of (12 V) and a current of (2 A) flowing through it. Calculate the power dissipated by the resistor.
Solution: Given; Voltage drop, (V = 12 V); Current, (I = 2 A)
Electric power is given by the product of voltage and current:
\(\displaystyle \text{Electric Power} = VI \)
\(\displaystyle \text{Electric Power} = 12 \times 2 \)
\(\displaystyle \text{Electric Power} = 24 \, \text{W} \)
Therefore, the power dissipated by the resistor is (24 W).
Example 5: A microwave oven consumes (1200 W) of power to heat food for (5 minutes). Calculate the energy consumed by the microwave oven.
Solution: Given; Power consumed by the microwave oven, (P = 1200 W); Time taken, (t = 5 minutes = 300 s)
Energy consumed is given by the product of power and time:
\(\displaystyle \text{Energy consumed} = Pt \)
\(\displaystyle \text{Energy consumed} = 1200 \times 300 \)
\(\displaystyle\text{Energy consumed} = 360000 \, \text{J} \)
Therefore, the energy consumed by the microwave oven is (360000 J).
Example 6: A weightlifter lifts a mass of (100 kg) to a height of (2 m) in (5 s). Calculate the average mechanical power developed by the weightlifter.
Solution: Given; Mass lifted, (m = 100 kg); Height lifted, (h = 2 m); Time taken, (t = 5 s); Acceleration due to gravity, (g = 9.8 m/s2)
The work done by the weightlifter is equal to the gravitational potential energy gained by the mass:
\(\displaystyle W = mgh \)
\(\displaystyle W = 100 \times 9.8 \times 2 \)
\(\displaystyle W = 1960 \, \text{J} \)
Average mechanical power is given by:
\(\displaystyle \text{Average Mechanical Power} = \frac{\text{Work done}}{\text{Time taken}} \)
\(\displaystyle \text{Average Mechanical Power} = \frac{1960}{5} \)
\(\displaystyle \text{Average Mechanical Power} = 392 \, \text{W} \)
Therefore, the average mechanical power developed by the weightlifter is (392 W).
Example 7: A wind turbine generates (1 MW) of power continuously. Calculate the energy generated by the wind turbine in (1 hour).
Solution: Given; Power generated by the wind turbine, (P = 1 MW = 1 × 106 W); Time, (t = 1 hour = 3600 s)
Energy generated ((E)) is given by the formula:
\(\displaystyle E = Pt \)
\(\displaystyle E = 1 \times 10^6 \times 3600 \)
\(\displaystyle E = 3.6 \times 10^9 \, \text{J} \)
Therefore, the energy generated by the wind turbine in (1 hour) is (3.6 × 109 J).
FAQs
What is power in physics, and how is it different from energy?
Power is the rate at which energy is transferred or work is done, while energy is the capacity to do work. Power is the rate of energy change with respect to time. In other words, power measures how quickly work is done or energy is transferred.
Can you explain the difference between average power and instantaneous power?
Average power is the average rate at which energy is transferred or work is done over a period of time. It is calculated by dividing the total work done or energy transferred by the time taken. Instantaneous power, on the other hand, is the power at any given instant in time, representing the rate of energy transfer or work done at that specific moment.
How is electric power calculated, and what are its units?
Electric power is the rate at which electrical energy is transferred or consumed by an electrical device. It is calculated by multiplying the voltage (V) across the device by the current (I) passing through it. The formula for electric power is (P = VI). The SI unit of power is the watt (W), where 1 watt is equal to 1 joule per second (J/s).
What is mechanical power, and how is it related to force and velocity?
Mechanical power is the rate at which work is done or energy is transferred in a mechanical system. It is calculated by multiplying the force (F) applied to an object by its velocity (v). The formula for mechanical power is (P = Fv). Mechanical power measures how quickly work is done to move an object against a resistance or force.
How does the consumption of energy relate to power usage?
The consumption of energy refers to the amount of energy used or consumed by a device, system, or process over a certain period of time. Power usage, on the other hand, refers to the rate at which energy is consumed. The higher the power usage, the faster energy is consumed, leading to higher energy consumption over time.
Can you provide examples of devices with high power consumption?
Examples of devices with high power consumption include electric heaters, air conditioners, electric ovens, and high-power industrial machinery. These devices require large amounts of electrical energy to operate and typically have higher power ratings compared to other household or industrial appliances.
How does understanding power consumption help in energy conservation efforts?
Understanding power consumption helps in identifying energy-efficient practices and technologies that reduce energy usage and waste. By optimizing power consumption, individuals, businesses, and governments can lower energy bills, reduce environmental impact, and contribute to sustainability efforts.
How does the concept of power relate to everyday activities and decision-making?
Power is relevant to everyday activities and decision-making, as it influences the efficiency, performance, and cost of various tasks and processes. For example, choosing energy-efficient appliances or vehicles can lower electricity bills and reduce carbon emissions. Understanding power also helps in evaluating the impact of different actions on energy usage and resource management.