Rigid Body

The study of rigid bodies dates back to the early days of classical mechanics, a branch of physics that deals with the motion of objects. The concept of a rigid body is essential because it simplifies the complex interactions of particles in a solid object by considering the object as a whole.

The idea of rigid bodies can be traced back to ancient Greek philosophers like Aristotle, who pondered the nature of matter and motion. However, it was not until the Renaissance that significant progress was made. Galileo Galilei, often called the father of modern science, made crucial observations about the motion of objects, laying the groundwork for later studies on rigid bodies.

The real breakthrough came with Sir Isaac Newton’s Philosophiæ Naturalis Principia Mathematica, commonly known as the Principia, published in 1687. Newton’s laws of motion formed the foundation for the study of the dynamics of rigid bodies. His first law, the law of inertia, implies the concept of a rigid body by stating that an object will remain at rest or in uniform motion unless acted upon by an external force.

Leonhard Euler, in the 18th century, expanded on Newton’s work by developing the equations of motion for rigid bodies. He introduced concepts like the body’s rotation around a fixed axis and the distribution of mass around this axis, which are key to understanding rigid body dynamics.

During the Industrial Revolution, the study of rigid bodies became increasingly important for designing and analyzing machinery. Engineers used the principles of rigid body dynamics to understand how forces and torques would affect the motion of machine parts.

In the 20th century, the field of rigid body dynamics continued to evolve with advancements in mathematics and computational methods. This allowed for more complex systems to be modeled and simulated, furthering our understanding of how rigid bodies behave under various conditions.

What is a Rigid Body?

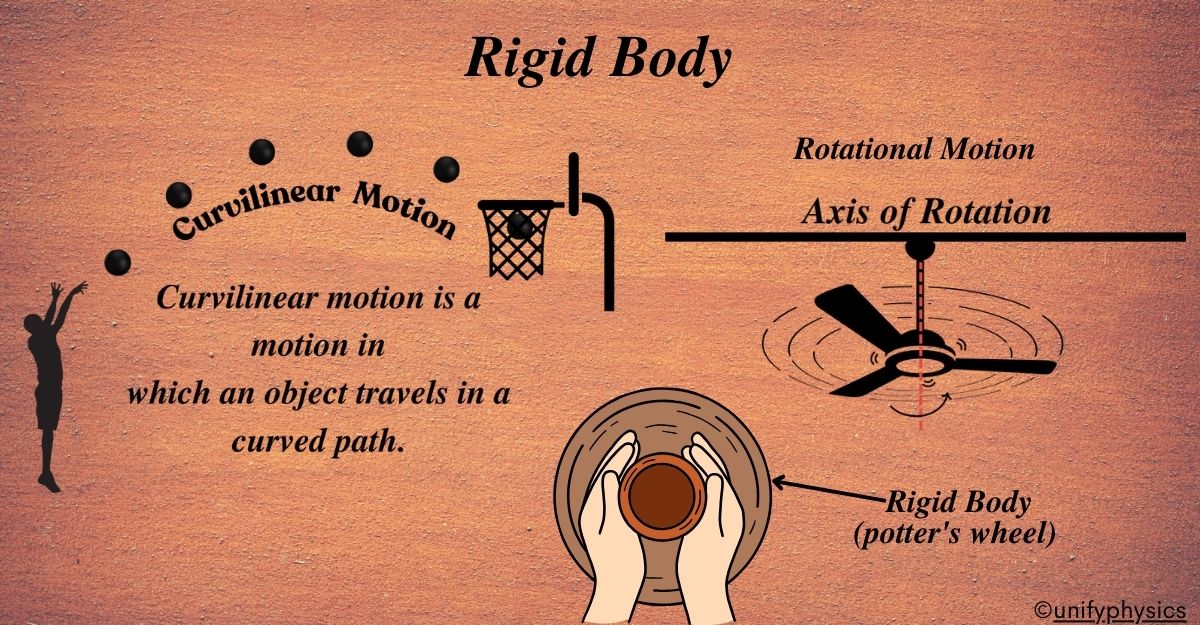
A rigid body is an idealized solid object where the distance between any two points within it remains constant, no matter what external forces or torques are applied. This means that the body does not deform or bend—it stays the same shape.

Imagine you have a toy car made of metal. No matter how you push or pull it, the car keeps its shape. This is because, in our imagination, the car is a rigid body. A rigid body is an idealized object that does not bend, stretch, or change shape in any way, regardless of the forces applied to it.

In the real world, every material will deform a little bit when forces are applied, but in physics, we often simplify the situation by assuming objects are rigid bodies. This helps us predict how they will move without worrying about them bending or breaking.

Characteristics of a Rigid Body:

• Unchanging Shape: The distances between any two points on a rigid body remain constant. If you measure the length of your toy car from the front bumper to the back, it will always be the same, no matter what.
• Indeformable: A rigid body doesn’t deform, which means it doesn’t stretch, compress, or bend. It’s like having an indestructible toy that can’t be squished or pulled apart.
• Simplified Model: By treating objects as rigid bodies, physicists can focus on motion and forces without getting bogged down by the complexities of materials and their properties.

Examples:

As the wheel rotates, it provides a stable platform for the potter to work on, allowing them to shape the clay with precision.

• Fan Blades: The blades of a fan rotate at high speeds, but they don’t stretch out or change shape; they are considered rigid bodies to study their motion.

Rigid Body Dynamics

Rigid body dynamics is the study of the motion of rigid bodies. Unlike particles, which only have mass and move in space, rigid bodies have size and shape and can perform complex motions, including rotation about an axis.

Imagine you’re at an amusement park, and you see a merry-go-round spinning. The horses and seats are moving, but they aren’t changing shape or flying off; they’re just rotating around the center. This is an example of Rigid Body Dynamics in action.

Understanding Rigid Body Dynamics helps us predict how objects will behave when forces are applied. This is crucial for everything from designing safe cars to creating realistic animations in video games.

• Rotation: Just like the merry-go-round, rigid bodies can spin around an axis. This is called rotational motion.
• Translation: Rigid bodies can also move from one place to another in a straight line, which is known as translational motion.
• Combination: Often, objects will do both at the same time—like a rolling ball, which spins (rotates) and moves across the floor (translates).
• Forces and Torques: Forces push or pull on objects, while torques cause them to rotate. The equations of motion for rigid bodies involve both of these.
• Euler’s Equations: These are special formulas that describe the rotation of a rigid body. They’re named after Leonhard Euler, a mathematician who made significant contributions to the field.

Examples:

• Sports: When a gymnast flips through the air, they’re controlling their body’s rotation to land safely.
• Engineering: Bridges and buildings are designed considering Rigid Body Dynamics to ensure they can withstand forces like wind and earthquakes.

Translational Motion

Translational motion occurs when a rigid body moves along a path without rotating. Every point on the body moves the same distance, in the same direction, and at the same time. Think of it like sliding a book across a table—it moves from one place to another without turning.

Imagine you’re on a skateboard. When you push off the ground and glide straight down the sidewalk, your entire body and the skateboard move together in the same direction. This is Translational Motion.

Translational Motion occurs when all points of a body move in the same line or direction, maintaining the same orientation. It’s like moving from point A to point B in a straight line without turning or spinning.

Types of Translational Motion:

Rectilinear Motion

Rectilinear Motion is a type of translational motion where an object moves along a straight line. It’s the simplest form of motion because everything moves in the same direction and at the same speed. For example, a car driving down a straight road is experiencing rectilinear motion.

Imagine you’re on a bus on a long, straight highway. The bus is moving forward, and everything inside the car is moving — your phone, your backpack, and even the air around you. This is Translational Motion, specifically Rectilinear Motion.

For instance, when the bus accelerates, all passengers inside the bus feel themselves being pushed backward due to inertia, which is the tendency of objects to resist changes in their motion. Similarly, when the bus decelerates, passengers feel themselves being pushed forward.

During this translational motion, the bus’s position changes over time relative to a fixed reference point, such as a mile marker along the highway. The bus’s speed and direction of travel determine how quickly and in which direction it moves along the highway.

Characteristics of Rectilinear Motion:

• Straight Path: The object’s path doesn’t curve or change direction.
• Uniform Motion: All parts of the object move together, maintaining the same orientation throughout the motion.
• Same Velocity: Every point on the object has the same velocity at any given instant.

Examples in Daily Life:

• A Train on Tracks: A train moving on straight tracks is in rectilinear motion because it doesn’t turn or rotate as it moves.
• An Arrow in Flight: When an archer shoots an arrow, and it flies straight toward the target, that’s rectilinear motion.
• Elevator: Think of an elevator. Whether it’s going up or down, every part of the elevator and everything inside it moves together in the same direction. That’s translational motion.

Curvilinear Motion

When the path is curved, like a roller coaster car following the twists and turns of the track, it’s curvilinear motion. Imagine you’re on a roller coaster. As it zooms around the track, it curves up, down, and all around. This is a Curvilinear Motion.

Curvilinear Motion is when an object moves along a curved path. Unlike rectilinear motion, where the path is straight, curvilinear motion involves changes in direction along a curve.

Let’s illustrate curvilinear motion using the example of throwing a basketball into a hoop. When a basketball player shoots the ball toward the basket, the ball follows a curved path due to the force exerted on it and the effects of gravity.

As the basketball travels through the air, its speed and direction change continuously due to the combined effects of the initial velocity, gravity, air resistance, and any other external forces acting on it. The path followed by the basketball is a curve, with the shape of the curve determined by the magnitude and direction of these forces.

Characteristics of Curvilinear Motion:

• Curved Path: The object’s path is not straight but curved, like the tracks of a roller coaster or the orbit of a planet around the sun.
• Changing Direction: Even if the object’s speed is constant, its velocity changes because velocity also depends on direction.
• Vector Description: Because the motion is along a curve, we use vectors to describe the position, velocity, and acceleration of the object at any point in time.

Examples:

• Driving on a Winding Road: When you drive a car around a bend, you’re experiencing curvilinear motion.
• A Ball Thrown in the Air: If you throw a ball, it follows a curved path as it goes up and then comes down, which is another example of curvilinear motion.

Curvilinear motion is important because it describes the motion of objects following a curved path, which is very common in the real world.

In Curvilinear motion, Every part of the moving body has the same velocity at any given moment. The body doesn’t rotate; it only moves from one location to another. The entire body moves uniformly in the same direction.

Also Read: Projectile Motion

Rotational Motion

Rotational motion is when a rigid body spins around a fixed axis. Every point on the body follows a circular path around this axis, and all points turn through the same angle over a given time period. A classic example is a spinning wheel or merry-go-round, anything that turns or spins is exhibiting rotational motion..

Rotational motion involves the movement of an object as it rotates around an axis. In other words, instead of moving from one place to another like in translational motion, the object rotates around a fixed point or axis.

As the blades rotate, they sweep through the air, creating airflow and cooling effects in the room.

In this example, the fan blades experience rotational motion because they rotate around a fixed axis. The rotational motion of the blades can be described in terms of angular displacement, angular velocity, and angular acceleration.

• Angular displacement refers to the angle through which the fan blades rotate around the axis.
• Angular velocity describes how quickly the blades rotate, measured in radians per second (rad/s).
• Angular acceleration represents how quickly the angular velocity changes over time.

The rotational motion of the ceiling fan can be controlled by adjusting the speed of the motor, which determines how fast the blades rotate. Additionally, the direction of rotation can be changed by reversing the motor’s direction.

Characteristics of Rotational Motion:

• Axis of Rotation: This is the imaginary line that the object spins around. It can be inside the object, like the axle of a wheel, or outside it, like the Earth rotating around its axis.
• Angular Displacement: It measures how far the object has rotated and is usually expressed in degrees or radians.
• Angular Velocity: This tells us how fast the object is rotating. It’s the rate of change of angular displacement over time.
• Angular Acceleration: If the object speeds up or slows down its rotation, it’s experiencing angular acceleration.

Examples:

• A Spinning Top: When you spin a top, it rotates around its axis.
• Wheels on a Car: As the car moves, the wheels rotate around their axles.

Conditions For Equilibrium

Think of a seesaw in a playground. When two children of equal weight sit at equal distances from the pivot, the seesaw is balanced. It doesn’t move up or down and stays in a horizontal position. This is an example of equilibrium.

Equilibrium occurs when all the forces and torques (rotational forces) acting on an object are balanced. In this state, the object is either at rest or moving with a constant velocity, and it’s not accelerating or rotating.

First Condition of Equilibrium (Translational Equilibrium):

The first condition is that the net force acting on the object must be zero. This means that all the forces cancel each other out. If you push a book on a table with your finger, and it doesn’t move, it’s because the force of your push is balanced by the frictional force of the table.

Imagine you’re playing tug-of-war. When both teams are pulling with the same strength, the rope doesn’t move to either side. This is because the forces are balanced, and the system is in Translational Equilibrium.

Translational Equilibrium occurs when the net force acting on an object is zero. This means that all the forces acting on the object cancel each other out, resulting in no change in the object’s velocity.

Characteristics of Translational Equilibrium:

• No Acceleration: The object does not speed up, slow down, or change direction. It either remains at rest or moves at a constant velocity.
• Balanced Forces: Forces acting in opposite directions are of equal magnitude, so they balance out.
• Vector Sum of Forces: When you add up all the forces acting on the object (considering their direction), the total (vector sum) is zero.

Examples:

• A Book on a Table: A book lying on a table is in translational equilibrium because the force of gravity pulling it down is balanced by the table pushing it up.
• A Car Cruising at Constant Speed: A car moving at a steady speed on a straight road is in translational equilibrium because the engine’s forward force is balanced by air resistance and friction.

Second Condition of Equilibrium (Rotational Equilibrium):

The second condition is that the net torque must also be zero. Torque is a measure of how much force acting on an object causes that object to rotate. So, if you apply forces on opposite ends of a ruler and it doesn’t spin, the torques are balanced.

Imagine you’re playing on a seesaw with a friend. If you and your friend are of equal weight and sit at equal distances from the pivot, the seesaw will stay level and not rotate. This is because it’s in Rotational Equilibrium.

Rotational Equilibrium occurs when the net torque acting on an object is zero. A torque is a force that causes an object to rotate. When the total torque is zero, it means there’s no unbalanced force causing the object to start spinning or to stop if it’s already spinning.

Characteristics of Rotational Equilibrium:

• No Angular Acceleration: The object does not speed up or slow down its rotation.
• Balanced Torques: Torques acting in opposite directions are of equal magnitude, so they balance out.
• Vector Sum of Torques: When you add up all the torques acting on the object (considering their direction), the total (vector sum) is zero.

Examples:

• A Balanced Wheel: A bicycle wheel spinning at a constant speed is in rotational equilibrium because no unbalanced torques are acting on it.
• A Hanging Sign: A sign hanging from a chain is in rotational equilibrium when it’s not rotating, meaning the torques from the weight of the sign and the support of the chain cancel each other out.

Understanding rotational equilibrium is essential for solving physics problems involving rotation and for designing objects that rotate, like wheels, gears, and turbines. It ensures that they rotate smoothly without unexpected speed changes.

Static vs. Dynamic Equilibrium:

• Static Equilibrium: The object is at rest. For example, a book lying on a table is in static equilibrium because it’s not moving.
• Dynamic Equilibrium: The object moves with a constant velocity. For example, a car cruising at a steady speed on a straight road is in dynamic equilibrium because it’s not accelerating.

Properties of a Rigid Body

When we talk about a rigid body in physics, we’re referring to an idealized object that doesn’t change shape or size, no matter what forces are applied to it. Here are some key properties:

Constant Shape and Size:
The defining property of a rigid body is that its shape and size remain unchanged. No matter what external forces you apply, the distances between any two points on the body stay the same.

Fixed Internal Structure:
Inside a rigid body, all the particles maintain a fixed spatial relationship with each other. This means that if you were to draw a line between any two particles within the body, that line would always be the same length, even if the body is moving or forces are acting on it.

Infinite Stiffness (In Theory):
In theory, a rigid body has infinite stiffness or rigidity. This means it would be completely resistant to any forces trying to change its shape. In reality, all materials will deform under enough force, but the concept of infinite stiffness is useful for simplifying problems in physics.

Zero Strain:
When forces are applied to a rigid body, it experiences zero strain. Strain is a measure of deformation, and since a rigid body does not deform, the strain is always zero.

Moment of Inertia:
This is a property that measures how much a body resists angular acceleration. If you try to spin a rigid body, its moment of inertia will determine how difficult it is to start or stop the spinning. It depends on the mass distribution of the body relative to the axis of rotation.

Center of Mass:
The center of mass is the point where you could balance the rigid body on the tip of a pencil, and it would stay perfectly balanced. It’s the average position of all the mass in the body.

Resistance to External Forces:
A rigid body resists changes in motion due to external forces. This is related to its mass and the distribution of that mass. The more mass and the more spread out it is, the more the body resists changes in motion.

These properties help us understand and predict how rigid bodies move and interact with forces, which is essential for solving many problems in physics.

Solved Examples

Example 1: A car travels along a straight road with an initial velocity of (20 m/s). If it accelerates uniformly at (3 m/s²) for (10 s), what is its final velocity?

Solution: Using the equation of motion for uniformly accelerated motion: \(\displaystyle v = u + at \)

Given (u = 20 m/s), (a = 3 m/s²), and (t = 10 s), we can calculate the final velocity:

\(\displaystyle v = 20 + (3 \times 10) \)
\(\displaystyle v = 20 + 30 \)
\(\displaystyle v = 50 \, \text{m/s} \)

Therefore, the final velocity of the car is (50 m/s).

Example 2: A particle moves along a curved path described by the equation (x² + y² = 25), where (x) and (y) are coordinates in meters. Find the velocity of the particle when (x = 3 m) and (y = 4 m).

Solution: To find the velocity of the particle, we need to differentiate the position vector with respect to time and then evaluate it at the given point.

Given the equation of the curve, we can express (y) in terms of (x):

\(\displaystyle y = \sqrt{25 – x^2} \)

Differentiating both sides with respect to (x), we get:

\(\displaystyle \frac{dy}{dx} = -\frac{x}{\sqrt{25 – x^2}} \)

At the point (x = 3 m) and (y = 4 m), we can substitute these values into the expression for \(\displaystyle\frac{dy}{dx}\):

\(\displaystyle \frac{dy}{dx} = -\frac{3}{\sqrt{25 – 9}} \)
\(\displaystyle \frac{dy}{dx} = -\frac{3}{4} \, \text{m/m} \)

Now, we need to find \(\displaystyle\frac{dx}{dt}\) and \(\displaystyle\frac{dy}{dt}\) using the chain rule. Then, we can find the velocity vector:

\(\displaystyle v = \sqrt{\left(\frac{dx}{dt}\right)^2 + \left(\frac{dy}{dt}\right)^2} \)

Substituting the known values:

\(\displaystyle v = \sqrt{\left(\frac{dx}{dt}\right)^2 + \left(-\frac{3}{4}\right)^2} \)

Solve for \(\displaystyle\frac{dx}{dt}\) using the given information.

Example 3: A wheel of radius (0.5 m) starts from rest and accelerates uniformly to an angular velocity of (10 rad/s) in (4 s). What is its angular acceleration?

Solution: Using the equation of rotational motion for uniformly accelerated rotation: \(\displaystyle \omega = \omega_0 + \alpha t \)

Given (ω = 10 rad/s), (ω₀ = 0 rad/s), and (t = 4 s), we can solve for (α):

\(\displaystyle 10 = 0 + \alpha \times 4 \)
\(\displaystyle \alpha = \frac{10}{4} \)
\(\displaystyle \alpha = 2.5 \, \text{rad/s}^2 \)

Therefore, the angular acceleration of the wheel is (2.5 rad/s²).

Example 4: A uniform beam of length (6 m) and mass (30 kg) is supported horizontally by two vertical strings attached to its ends. If a (50 kg) mass hangs from the midpoint of the beam, find the tension in each string.

Solution: For the beam to be in equilibrium, the net force and net torque acting on it must be zero. First, calculate the total weight acting downward on the beam:

\(\displaystyle W_{\text{beam}} = m_{\text{beam}} \times g = 30 \times 9.8 \, \text{N} = 294 \, \text{N} \)

Since the beam is uniform and supported at its ends, the tension in each string will be equal. Let (T) be the tension in each string. Considering the forces in the vertical direction:

\(\displaystyle 2T = W_{\text{beam}} + m_{\text{hanging}} \times g \)
\(\displaystyle 2T = 294 + 50 \times 9.8 \)
\(\displaystyle 2T = 294 + 490 \)
\(\displaystyle 2T = 784 \)
\(\displaystyle T = \frac{784}{2} = 392 \, \text{N} \)

Therefore, the tension in each string is (392 N).

Example 5: A ladder of length (5 m) rests against a smooth wall and a rough floor making an angle of (60^∘) with the floor. If the ladder is in equilibrium and the coefficient of friction between the ladder and the floor is (0.4), find the minimum and maximum forces of friction acting on the ladder.

Solution: The ladder is in equilibrium, so the sum of forces and the sum of torques acting on it must be zero.

• (N) as the normal reaction force from the floor
• (F_f) as the frictional force
• (F) as the force applied to the ladder
• (W) as the weight of the ladder
• (θ) as the angle the ladder makes with the floor
• (R) as the reaction force from the wall

Since the ladder is in equilibrium, we have:

\(\displaystyle \sum{{{{F}_{x}}}}=0\Rightarrow F-{{F}_{f}}=0\Rightarrow F={{F}_{f}}\)

\(\displaystyle \sum{{{{F}_{y}}}}=0\Rightarrow N-W=0\Rightarrow N=W\)

The maximum frictional force is given by:

\(\displaystyle F_{f_{\text{max}}} = \mu N = \mu W \)

\(\displaystyle F_{f_{\text{max}}} = 0.4 \times W \)

\(\displaystyle F_{f_{\text{max}}} = 0.4 \times (5 \times 9.8) \)

\(\displaystyle F_{f_{\text{max}}} = 19.6 \, \text{N} \)

The minimum frictional force is zero since the ladder is in equilibrium and there’s no motion. Therefore, the minimum frictional force is (0N) and the maximum frictional force is (19.6 N).

Example 6: A plank of length (4 m) and mass (10 kg) is supported by two ropes at its ends making angles of (30^∘) and (60^∘) with the horizontal. Find the tension in each rope.

Solution: The plank is in equilibrium, so the sum of forces in both the horizontal and vertical directions must be zero.

• (T₁) as the tension in the first rope
• (T₂) as the tension in the second rope

Since the plank is in equilibrium, we have:

\(\displaystyle \sum{{{{F}_{x}}}}=0\Rightarrow {{T}_{1}}\cos ({{30}^{0}})-{{T}_{2}}\cos ({{60}^{0}})=0\)

\(\displaystyle \sum{{{{F}_{y}}}}=0\Rightarrow {{T}_{1}}\sin ({{30}^{0}})+{{T}_{2}}\sin ({{60}^{0}})-W=0\)

Where (W) is the weight of the plank given by \(\displaystyle W = mg = 10 \times 9.8 \, \text{N}\).

From the first equation:

\(\displaystyle T_1\cos(30^\circ) = T_2\cos(60^\circ) \)
\(\displaystyle T_1\cos(30^\circ) = T_2\left(\frac{1}{2}\right) \)
\(\displaystyle T_1 = \frac{1}{\sqrt{3}}T_2 \)

Substitute this expression for (T₁) into the second equation:

\(\displaystyle T_1\sin(30^\circ) + T_2\sin(60^\circ) – W = 0 \)
\(\displaystyle \left(\frac{1}{2}T_2\right) + \left(\frac{\sqrt{3}}{2}T_2\right) – 98 = 0 \)
\(\displaystyle \frac{3}{2}T_2 – 98 = 0 \)
\(\displaystyle T_2 = \frac{98 \times 2}{3} = 65.33 \, \text{N} \)

Now, substitute (T₂) into the expression for (T₁):

\(\displaystyle T_1 = \frac{1}{\sqrt{3}} \times 65.33 \)
\(\displaystyle T_1 = 37.78 \, \text{N} \)

Therefore, the tension in the first rope is (37.78 N) and the tension in the second rope is (65.33 N).

Example 7: A uniform beam of length (8 m) and mass (40 kg) is placed horizontally on two supports. A (60 kg) person sits (2 m) from one end. Find the reactions at the supports.

Solution: To solve this problem, we’ll use the conditions for equilibrium.

Let (R₁) and (R₂) be the reactions at the supports. Since the beam is in equilibrium, the sum of forces in both the vertical and horizontal directions must be zero.

In the vertical direction:

\(\displaystyle R_1 + R_2 – (40 \times 9.8) – (60 \times 9.8) = 0 \)
\(\displaystyle R_1 + R_2 = 392 + 588 = 980 \, \text{N} \)

In the horizontal direction:

\(\displaystyle R_1 \times 8 – (60 \times 9.8 \times 2) = 0 \)
\(\displaystyle R_1 \times 8 = 1176 \)
\(\displaystyle R_1 = \frac{1176}{8} = 147 \, \text{N} \)

From the first equation:

\(\displaystyle R_2 = 980 – R_1 = 980 – 147 = 833 \, \text{N} \)

Therefore, the reactions at the supports are (R₁ = 147 N) and (R₂ = 833 N).

FAQs