The phenomenon of reflection has been observed and pondered upon since ancient times. The earliest humans saw their reflections in water, perhaps their first encounter with this natural optical effect.
As civilizations advanced, the desire to see oneself led to the creation of the first mirrors. These were typically polished surfaces of natural materials like stone or metal. The Egyptians and Mesopotamians made mirrors from polished copper as early as 4000 BC.
The Greeks and Romans improved mirror-making techniques, using metals like bronze. However, these mirrors were small and did not have the clarity of modern mirrors. The scholars of this era, like Euclid, began to document the laws of reflection.
During the Middle Ages, glass mirrors backed with gold leaf were produced, but they were available only to the wealthy. The understanding of spherical mirrors began to develop, but it was not until the Renaissance that significant progress was made.
The Renaissance was a golden era for the study of optics. Artisans achieved breakthroughs in creating clearer, larger mirrors by coating glass with a tin-mercury amalgam. This period also saw the likes of Leonardo da Vinci and Alhazen making strides in the theoretical understanding of light and reflection.
The 17th century’s scientific revolution brought a more systematic study of light. Isaac Newton and others expanded our knowledge of optics, including the properties of spherical mirrors. The principles of concave and convex mirrors were established, leading to practical applications in telescopes and other instruments.
What is a Spherical Mirror?
A spherical mirror is essentially a piece of a reflective sphere. Imagine cutting out a small section of a shiny, hollow ball; that’s what a spherical mirror looks like. The main characteristic of these mirrors is their curved surface, which is part of a sphere.
There are two types of spherical mirrors, defined by the side on which they reflect light:
- Concave mirrors: These mirrors curve inward, like the inside of a spoon. They reflect light inwards towards a single point, known as the focus.
- Convex mirrors: These curve outward, like the back of a spoon, and spread light outwards. This means they don’t focus light to a point but rather reflect it over a wider area.
The curvature of these mirrors affects how they reflect light and form images, making them useful for various applications in daily life and technology. For instance, concave mirrors can focus light to a point, which is why they’re used in devices like telescopes and flashlights, while convex mirrors give a wider view and are used for car rearview mirrors. The curvature causes the mirror to reflect light differently than a flat mirror, leading to unique image formation properties.
Terminology of Spherical Mirrors:
- Center of Curvature (C): The center of the sphere from which the spherical mirror segment is taken. It lies outside the mirror for concave mirrors and behind the mirror for convex mirrors.
- The radius of Curvature (R): The radius of the sphere from which the mirror is made. It is the distance from the center of curvature to any point on the mirror.
- Pole (P): The midpoint of the mirror’s surface, it is the point on the mirror that lies closest to the object.
- Principal Axis: An imaginary line that passes through the pole and the center of curvature. It is perpendicular to the mirror at its pole.
- Aperture: The effective diameter of the mirror, it is the portion of the mirror through which light is reflected.
- Principal Focus (F): The point where light rays parallel to the principal axis converge (concave) or appear to diverge (convex) after reflection. For concave mirrors, this point is real and in front of the mirror; for convex mirrors, it is virtual and behind the mirror.
- Focus (f): The distance along the principal axis from the pole to the principal focus. It is half the radius of curvature ($$ f = \frac{R}{2} $$).
Types of Spherical Mirrors
Concave Mirrors
A concave mirror, also known as a converging mirror, is a spherical mirror with a reflective surface that curves inward, resembling the inside of a sphere. When you look at a concave mirror, you’ll notice that the center seems to be scooped out, and the edges curve towards you.
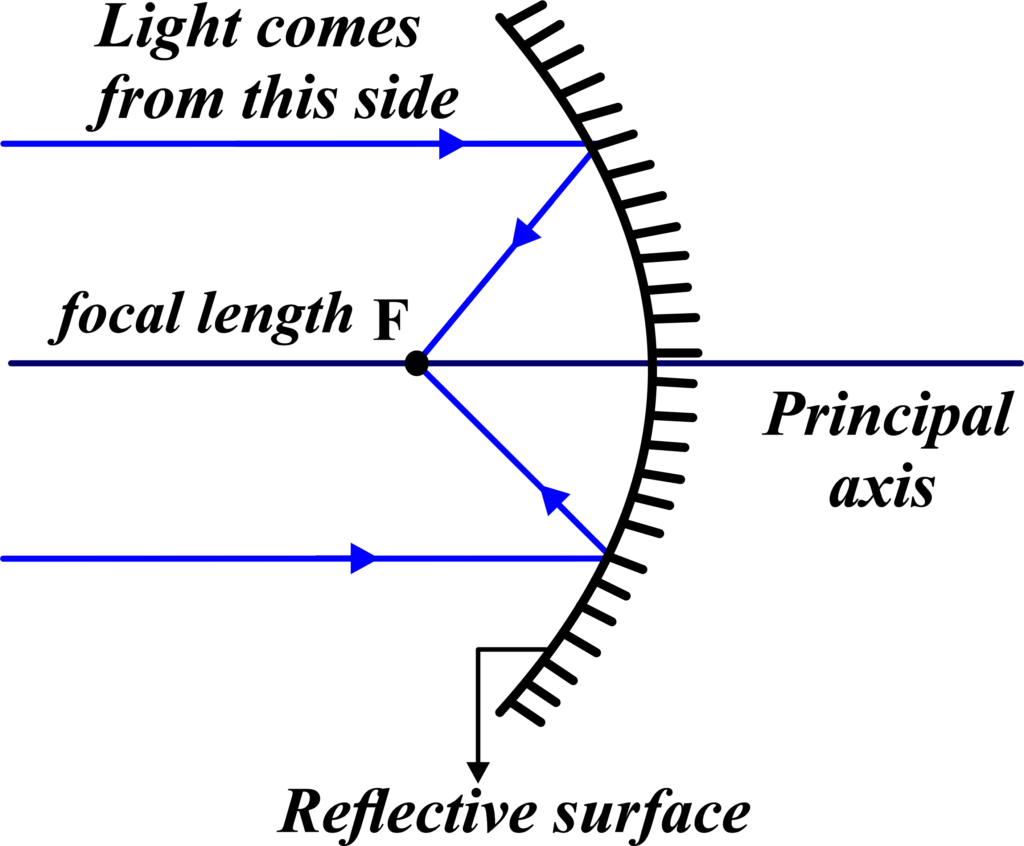
Concave mirrors reflect light rays inward towards a single focal point. This is why they are called converging mirrors. When parallel light rays hit a concave mirror, they reflect and meet at a point called the principal focus. This property allows concave mirrors to concentrate light, making them useful in applications where light needs to be focused, such as in flashlights or telescopes.
Image Formation: Depending on where an object is placed in relation to the mirror’s focal point, the image can appear larger or smaller, upright or inverted. For example, if you place an object very close to a concave mirror (closer than the focal point), you’ll see a magnified, upright image. But if you move the object beyond the focal point, the image becomes inverted.
The images formed by concave mirrors can vary greatly depending on the distance of the object from the mirror:
- At infinity: The image is formed at the focal point and is highly diminished.
- Beyond the center of curvature: The image is formed between the center of curvature and the focal point, inverted and reduced in size.
- At the center of curvature: The image is formed at the center of curvature, inverted and of the same size as the object.
- Between the center of curvature and the focal point: The image is formed beyond the center of curvature, inverted and magnified.
- At the focal point: No image is formed because the reflected rays are parallel.
- Between the focal point and the mirror: The image is formed on the same side as the object, upright, and magnified.
Convex Mirrors
A convex mirror, also known as a diverging mirror, is a type of spherical mirror with a reflective surface that bulges outward. It’s like the outer surface of a shiny ball. Imagine a shiny, round ball that’s been turned inside out. The outer surface of this ball is similar to a convex mirror. Unlike a concave mirror that caves inwards, a convex mirror bulges outwards.
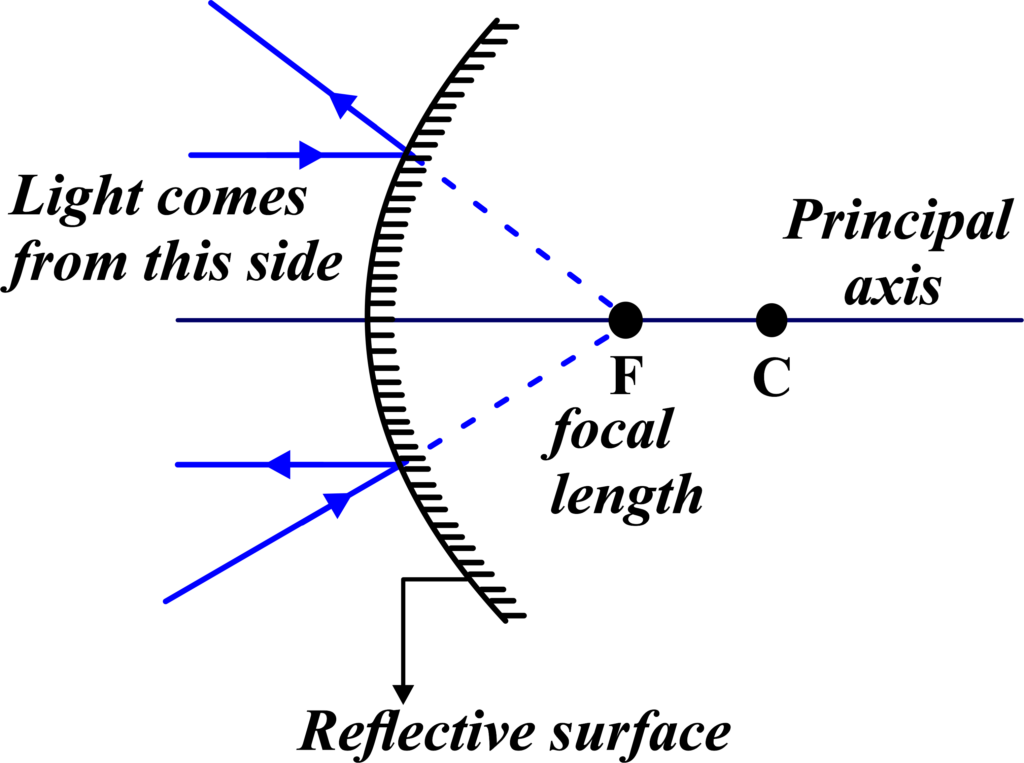
When light rays hit a convex mirror, they reflect off and spread out. This spreading out of light rays is known as divergence. Even though the light rays are diverging, they seem to be coming from a common point behind the mirror. This point is called the virtual focal point because the light rays don’t come together there; it just looks like they do.
Characteristics:
- Diverging Effect: Unlike concave mirrors that converge light, convex mirrors cause light rays to spread out or diverge. This is why they are called diverging mirrors.
- Field of View: Convex mirrors provide a wider field of view than concave mirrors. This is because they reflect light from a broader area.
- Image Formation: The images formed by convex mirrors are always virtual, upright, and smaller than the object, no matter where the object is placed in relation to the mirror.
- Focal Point: The focal point of a convex mirror is the point from which light rays appear to diverge after reflecting off the mirror. This point is virtual and cannot be reached by the light rays actually since it’s behind the mirror.
Sign Conventions for Spherical Mirrors
The sign conventions are a set of rules that help us determine the nature and position of images formed by spherical mirrors. They are based on a coordinate system where the mirror’s pole (the central point of the mirror’s surface) is considered the origin.
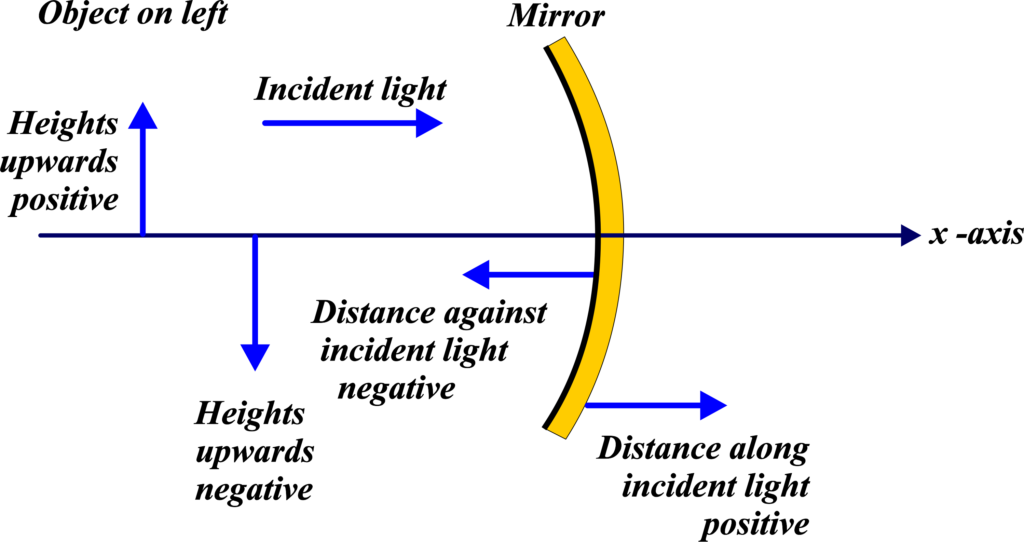
- Object Distance (u): The distance from the object to the mirror’s pole. It is considered negative if the object is in front of the mirror, which is the usual case.
- Image Distance (v): The distance from the image to the mirror’s pole. It is positive if the image is formed in front of the mirror (real image) and negative if formed behind the mirror (virtual image).
- Focal Length (f): The distance from the mirror’s pole to the focal point. For concave mirrors, it is positive, and for convex mirrors, it is negative because the focal point of a convex mirror is virtual and behind the mirror.
- Height of the Object (ho) and Image (hi): Heights are measured perpendicular to the principal axis. The height is positive if the object or image is above the principal axis and negative if below.
Heights:
- Above Principal Axis: Heights measured above the principal axis are considered positive.
- Below Principal Axis: Heights measured below the principal axis are considered negative.
Directions:
- Towards the Mirror: Distances measured in the direction of the incident light (towards the mirror) are considered negative.
- Away from the Mirror: Distances measured in the direction opposite to the incident light (away from the mirror) are considered positive.
These conventions are universally accepted and used to correctly apply the mirror and magnification formulas. They ensure consistency when determining the characteristics of the image formed by spherical mirrors.
Types of Images
Real Images:
- Formation: A real image is formed when light rays converge and meet at a point after reflecting off the mirror.
- Characteristics: They are inverted, meaning they appear upside down compared to the object. Real images can be projected onto a screen because they exist at a point in space where light converges.
- Example: The image formed on a cinema screen is a real image because it’s created by light rays that have converged to form a visible picture on a surface.
Virtual Images:
- Formation: A virtual image is formed when light rays diverge but appear to come from a common point when traced backward. The light does not meet at this point; it’s just an optical illusion.
- Characteristics: They are upright, meaning they maintain the same orientation as the object. Virtual images cannot be projected onto a screen because the light doesn’t come to a point.
- Example: The image you see in a flat bathroom mirror is virtual. It seems to be behind the mirror, and you cannot project it onto a screen.
These concepts are fundamental in understanding how mirrors affect the path of light and the nature of the images they produce. Real images are tangible in the sense that they can be captured on a screen, while virtual images are like mirages, visible but not physically present in the location they appear to be.
Image Formation by Spherical Mirrors
Images Formed by Concave Mirrors:
|
Position of Object |
Ray Diagram |
Position of Image |
Nature of Image |
At Infinity |
At the Focal Point (F) |
Real, Inverted, Highly Diminished |
Beyond the Center of Curvature (C) |
Between F and C |
Real, Inverted, Diminished |
At the Center of Curvature (C) |
At C |
Real, Inverted, Same Size |
Between C and Focal Point (F) |
Beyond C |
Real, Inverted, Magnified |
At the Focal Point (F) |
At Infinity |
Real, Inverted, Highly Magnified |
Between F and the Mirror |
Behind the Mirror |
Virtual, Upright, Magnified |
|---|
This table provides a concise overview of how the position of the object relative to the concave mirror affects the characteristics of the image formed.
Images Formed by Convex Mirrors:
|
Position of Object |
Ray Diagram |
Position of Image |
Nature of Image |
At Infinity |
At the Focal Point (F), behind the mirror |
Virtual, Upright, Highly Diminished |
Between Infinity and the Pole (P) |
Between the Pole (P) and the Focal Point (F), behind the mirror |
Virtual, Upright, Diminished |
|---|
In both cases, the images formed by convex mirrors are virtual, meaning they cannot be projected onto a screen, and they are upright and smaller than the object.
Focal Length (Spherical Mirrors)
The focal length of a spherical mirror is a key concept in optics. It’s the distance from the mirror’s surface to the point where light rays coming parallel to the principal axis converge (for concave mirrors) or appear to diverge (for convex mirrors).
For Concave Mirrors:
- The focal length is positive and is the distance from the mirror to the focal point on the same side as the reflected light.
- It’s where parallel light rays that strike the mirror converge after reflection.
For Convex Mirrors:
- The focal length is negative, indicating that the focal point is behind the mirror.
- It’s the point from which parallel light rays appear to diverge after reflecting off the mirror.
Relation between the Focal Point (F) and Radius of Curvature (R) of a Mirror
It’s the specific point where parallel rays of light either converge (in concave mirrors) or appear to diverge (in convex mirrors) after reflecting off the mirror. This is the radius of the sphere from which the mirror segment is taken. It represents the distance from the center of curvature to any point on the mirror’s surface. The relationship between the focal length (f), which is the distance from the mirror to the focal point, and the radius of curvature (R) is given by a simple formula:
\(\displaystyle\begin{equation}\label{eqn:1}\boxed{\boldsymbol{f = \frac{R}{2} }} \end{equation}\)
This means that the focal length is half the radius of curvature. This relationship holds true for both concave and convex spherical mirrors.
Mirror Equation
The mirror equation is a fundamental concept in the study of optics, particularly when dealing with spherical mirrors. It’s an equation that relates the object distance (u), the image distance (v), and the focal length (f) of a mirror. Here’s a simple explanation suitable for 12th-grade physics students:
The mirror equation is given by:
\(\displaystyle\begin{equation}\label{eqn:2}\boxed{\boldsymbol{\frac{1}{f} = \frac{1}{v} + \frac{1}{u} }} \end{equation}\)
- f (Focal Length): The distance between the mirror’s surface and its focal point. For concave mirrors, this is positive, and for convex mirrors, it’s negative.
- v (Image Distance): The distance from the mirror to the image formed by the mirror. It’s positive if the image is real and on the same side as the object, and negative if the image is virtual and appears behind the mirror.
- u (Object Distance): The distance from the object to the mirror. It’s always negative according to the sign convention, as the object is placed in front of the mirror.
If you know the object distance and the focal length, you can find the image distance, and vice versa. The equation tells us that if the object is far from the mirror (u is large), the image distance (v) will be close to the focal length (f). Conversely, if the object is close to the focal point, the image will form far from the mirror.
This equation is very powerful and is used to calculate the position and size of the image formed by a mirror. It applies to both concave and convex mirrors and works for all object positions.
Also Read: Reflection Of Light
Magnification Formula for Spherical Mirrors
Magnification (m) is defined as the ratio of the height of the image (hi) to the height of the object (ho). It also relates the image distance (v) to the object distance (u).
The magnification formula is:
\(\displaystyle m = \frac{h_i}{h_o} = -\frac{v}{u} \)
The magnification is first considered as the ratio of the image height to the object height.
\(\displaystyle m = \frac{h_i}{h_o} \)
In the case of spherical mirrors, particularly concave mirrors, when an object is placed in front of the mirror, an image is formed. By drawing the object and the image to scale, we can observe two similar triangles. The triangle formed by the object and the principal axis, and the triangle formed by the image and the principal axis are similar by geometry.
Because these triangles are similar, the sides are proportional. The height of the image (hi) is related to the height of the object (ho), just as the image distance (v) is related to the object distance (u).
\(\displaystyle \frac{h_i}{h_o} = -\frac{v}{u} \)
The negative sign in the formula accounts for the inversion of the image. In concave mirrors, when the image is real, it is inverted, and thus the image height is considered negative. Combining the ratios of the heights and distances, we get the magnification formula for spherical mirrors.
\(\displaystyle m = \frac{h_i}{h_o} = -\frac{v}{u} \)
This formula tells us that the magnification is negative when the image is real and inverted, and positive when the image is virtual and upright. It’s a powerful tool in optics that helps us understand the relationship between the object and its image formed by a spherical mirror.
Uses of Spherical Mirrors
Spherical mirrors are not just fascinating physics concepts; they have practical uses in our daily lives and various technologies.
Uses of Concave Mirrors:
- Focusing Light: Due to their converging properties, concave mirrors are used to focus light. This makes them ideal for use in flashlights and headlights of vehicles, where they concentrate light into a beam.
- Telescopes: In astronomical telescopes, concave mirrors are used to gather light from distant stars and planets and bring them to a focus, where the image can be observed or photographed.
- Medical and Dental Instruments: Concave mirrors are used in ENT mirrors and dental mirrors because they can produce magnified images of small areas.
- Solar Furnaces: They are used in solar cookers and solar furnaces to focus sunlight to a point, generating heat for cooking or industrial processes.
Uses of Convex Mirrors:
- Wide-Angle Viewing: Convex mirrors are used as rear-view mirrors on vehicles because they provide a wider field of view, reducing blind spots.
- Security: In stores and public spaces, convex mirrors allow for a panoramic view, making them useful for security purposes.
- Street Safety: At intersections, convex mirrors give drivers a better view of oncoming traffic, enhancing road safety.
These are just a few examples of how spherical mirrors are utilized based on their unique properties of image formation.
Solved Examples
Example 1: A concave mirror has a focal length of 12 cm. An object is placed 18 cm from the mirror. Calculate the position and nature of the image formed.
Solution: We use the mirror equation:
\(\displaystyle\frac{1}{f} = \frac{1}{u_o} + \frac{1}{v_i}\)
Given: Focal length (f) = -12 cm (negative for concave mirrors); Object distance (uo) = 18 cm
Substitute the values:
\(\displaystyle\frac{1}{-12} = \frac{1}{18} + \frac{1}{v_i}\)
Rearrange to solve for (vi):
\(\displaystyle\frac{1}{v_i} = \frac{1}{-12} – \frac{1}{18}\)
\(\displaystyle\frac{1}{v_i} = -\frac{3}{36} – \frac{2}{36}\)
\(\displaystyle\frac{1}{v_i} = -\frac{5}{36}\)
\(\displaystyle v_i = -7.2 \text{ cm}\)
The image is formed 7.2 cm in front of the mirror, indicating that the image is real and inverted.
Example 2: An object 4 cm high is placed 16 cm in front of a concave mirror with a focal length of 8 cm. Determine the height and nature of the image.
Solution: First, find the image distance (vi) using the mirror equation:
\(\displaystyle\frac{1}{f} = \frac{1}{u_o} + \frac{1}{v_i}\)
Given: Focal length (f) = -8 cm ; Object distance (uo) = 16 cm
Substitute the values:
\(\displaystyle\frac{1}{-8} = \frac{1}{16} + \frac{1}{v_i}\)
\(\displaystyle\frac{1}{v_i} = \frac{1}{-8} – \frac{1}{16}\)
\(\displaystyle\frac{1}{v_i} = -\frac{2}{16} – \frac{1}{16}\)
\(\displaystyle\frac{1}{v_i} = -\frac{3}{16}\)
\(\displaystyle v_i = -5.33 \text{ cm}\)
Next, calculate the magnification (m):
\(\displaystyle m = -\frac{v_i}{u_o} = -\frac{-5.33}{16} \approx 0.333\)
The height of the image (hi) is given by:
\(\displaystyle h_{i} = m \times h_o = 0.333 \times 4 \approx 1.33 \text{ cm}\)
The height of the image is approximately 1.33 cm, and it is real and inverted.
Example 3: A convex mirror has a focal length of 15 cm. An object is placed 30 cm from the mirror. Determine the position and nature of the image.
Solution: We use the mirror equation:
\(\displaystyle\frac{1}{f} = \frac{1}{u_o} + \frac{1}{v_i}\)
Given: Focal length (f) = 15 cm (positive for convex mirrors) ; Object distance (uo) = -30 cm (negative for convex mirrors)
Substitute the values:
\(\displaystyle\frac{1}{15} = \frac{1}{-30} + \frac{1}{v_i}\)
Rearrange to solve for (vi):
\(\displaystyle\frac{1}{v_i} = \frac{1}{15} – \frac{1}{-30}\)
\(\displaystyle\frac{1}{v_i} = \frac{2}{30} + \frac{1}{30}\)
\(\displaystyle\frac{1}{v_i} = \frac{3}{30}\)
\(\displaystyle v_i = 10 \text{ cm}\)
The image is formed 10 cm behind the mirror, indicating that the image is virtual, erect, and diminished.
Example 4: An object is placed 10 cm in front of a concave mirror, and the image formed is real and located 20 cm from the mirror. Calculate the focal length of the mirror.
Solution: We use the mirror equation:
\(\displaystyle\frac{1}{f} = \frac{1}{u_o} + \frac{1}{v_i}\)
Given: Object distance (uo) = 10 cm; Image distance (vi) = -20 cm (negative for real images in concave mirrors)
Substitute the values:
\(\displaystyle\frac{1}{f} = \frac{1}{10} + \frac{1}{-20}\)
\(\displaystyle\frac{1}{f} = \frac{2}{20} – \frac{1}{20}\)
\(\displaystyle\frac{1}{f} = \frac{1}{20}\)
\(\displaystyle f = 20 \text{ cm}\)
The focal length of the concave mirror is 20 cm.
Example 5: An object 3 cm high is placed 12 cm in front of a convex mirror with a focal length of 6 cm. Determine the height and nature of the image.
Solution: First, find the image distance (vi) using the mirror equation:
\(\displaystyle\frac{1}{f} = \frac{1}{u_o} + \frac{1}{v_i}\)
Given: Focal length (f) = 6 cm; Object distance (uo) = -12 cm (negative for convex mirrors)
Substitute the values:
\(\displaystyle\frac{1}{6} = \frac{1}{-12} + \frac{1}{d_i}\)
\(\displaystyle\frac{1}{v_i} = \frac{1}{6} – \frac{1}{-12}\)
\(\displaystyle\frac{1}{v_i} = \frac{2}{12} + \frac{1}{12}\)
\(\displaystyle\frac{1}{dv_i} = \frac{3}{12} = \frac{1}{4}\)
$latex \displaystyle v_i = 4 \text{ cm}
Next, calculate the magnification (m):
\(\displaystyle m = -\frac{v_i}{u_o} = -\frac{4}{-12} \approx 0.333\)
The height of the image (vi) is given by:
\(\displaystyle v_i = m \times h_o = 0.333 \times 3 \approx 1 \text{ cm}\)
The height of the image is approximately 1 cm, and it is virtual and erect.
Example 6: A concave mirror has a radius of curvature of 40 cm. An object is placed 30 cm from the mirror. Determine the position of the image.
Solution: First, find the focal length:
\(\displaystyle f = \frac{R}{2} = \frac{40}{2} = 20 \text{ cm}\)
Using the mirror equation:
\(\displaystyle z\frac{1}{f} = \frac{1}{u_o} + \frac{1}{v_i}\)
Given: Focal length (f) = -20 cm (negative for concave mirrors); Object distance (uo) = 30 cm
Substitute the values:
\(\displaystyle\frac{1}{-20} = \frac{1}{30} + \frac{1}{v_i}\)
Rearrange to solve for (vi):
\(\displaystyle\frac{1}{v_i} = \frac{1}{-20} – \frac{1}{30}\)
\(\displaystyle\frac{1}{v_i} = -\frac{3}{60} – \frac{2}{60}\)
\(\displaystyle\frac{1}{v_i} = -\frac{5}{60}\)
\(\displaystyle v_i = -12 \text{ cm}\)
The image is formed 12 cm in front of the mirror, indicating that the image is real and inverted.
FAQs
What are the main differences between concave and convex mirrors?
The main differences between concave and convex mirrors lie in their shapes and the way they reflect light. A concave mirror, which curves inward like the inside of a bowl, converges light rays to a focal point. Conversely, a convex mirror, which curves outward like the back of a spoon, diverges light rays, making them appear to come from a focal point behind the mirror.
How does a concave mirror form different types of images based on the object’s position?
A concave mirror forms different types of images depending on the object’s distance from the mirror. If the object is far from the mirror, the image is real, inverted, and reduced in size. As the object moves closer to the focal point, the image becomes larger. When the object is placed between the focal point and the mirror, the image is virtual, upright, and magnified.
Why are convex mirrors commonly used as rear-view mirrors in vehicles?
Convex mirrors are commonly used as rear-view mirrors in vehicles because they provide a wider field of view compared to flat or concave mirrors. The outward curvature of convex mirrors causes light rays to diverge, allowing drivers to see a larger area and reducing blind spots, thereby enhancing safety.
What is the significance of the focal point in the context of spherical mirrors?
The focal point of a spherical mirror is the point where parallel light rays converge (in concave mirrors) or appear to diverge (in convex mirrors) after reflection. It is significant because it determines the behavior of light and the nature of the image formed by the mirror, including its size, orientation, and type (real or virtual).
How do spherical mirrors differ from plane mirrors in terms of image formation?
Spherical mirrors differ from plane mirrors in that they can form both real and virtual images, whereas plane mirrors only form virtual images. A concave mirror can produce real images that can be projected onto a screen, while a convex mirror always forms virtual images. Plane mirrors produce images that are the same size as the object and are upright and laterally inverted.
Can you explain the concept of the center of curvature and its relevance to spherical mirrors?
The center of curvature of a spherical mirror is the center of the hypothetical sphere from which the mirror segment is taken. It is relevant because it helps in understanding the geometry and behavior of the mirror. The radius of curvature, which is the distance from the mirror’s surface to the center of curvature, influences the mirror’s focal length and the formation of images.
Why does a concave mirror produce a magnified image when the object is placed close to it?
A concave mirror produces a magnified image when the object is placed close to it (between the focal point and the mirror) because the reflected light rays diverge in such a way that they appear to be coming from a larger, upright virtual image. This property is utilized in applications like makeup mirrors, where magnification is desired.
