Refraction At A Spherical Surface

The concept of refraction through spherical surfaces has its roots in ancient civilizations. The Greeks were among the first to study optics, with scholars like Euclid and Ptolemy laying the groundwork for understanding light’s behavior. However, it was the Arab scientists during the Islamic Golden Age who significantly advanced the field, refining the theories of refraction and lens-making.

In the 10th century, the scholar Ibn Sahl documented the first correct law of refraction, known as Snell’s Law today. This discovery was crucial for understanding how light bends when it passes through different media, such as air and glass.

During the Renaissance, the study of refraction gained momentum with the works of Johannes Kepler and Willebrord Snellius. Kepler’s work on the optics of the eye led to a better understanding of how lenses can correct vision, while Snellius’ law of refraction provided a mathematical description of how light rays change direction when entering a new medium.

The 17th century saw further developments with scientists like René Descartes and Isaac Newton exploring the nature of light and its refraction. Descartes’ “Dioptrique” was a significant work that discussed the refraction of light through spherical surfaces and laid the foundation for lens design.

By the 18th and 19th centuries, the Industrial Revolution and advances in precision engineering allowed for the mass production of lenses and the development of sophisticated optical instruments like microscopes and telescopes. Today, the principles of refraction from spherical surfaces are applied in various fields, from corrective eyewear to advanced scientific equipment.

Refraction At A Spherical Surface

Refraction occurs when light passes from one medium to another, changing speed and bending due to a change in its wave’s speed. At a spherical surface, this bending is symmetrical around an axis known as the principal axis. Refraction at a spherical surface is all about light changing direction as it passes through a curved boundary between two materials.

Imagine you have a transparent sphere, like a glass marble. If you shine a light on it, the light will bend as it enters and exits the sphere. This bending is called refraction. Now, if you cut a thin slice off one side of the sphere, you’ll have a spherical surface, and the same bending of light occurs at this surface.

When light hits this spherical surface, it doesn’t go straight through. Instead, it changes direction. This happens because light travels at different speeds in different materials. In the case of our glass marble, light travels slower in glass than in air. So, when light enters the glass at an angle, it slows down and bends towards a line we call the ‘normal’—an imaginary line perpendicular to the surface at the point of contact.

The amount of bending depends on two things:

1. The angle at which the light hits the surface.
2. The difference in the speed of light in the two materials is characterized by their refractive indices.

This concept is crucial for understanding how lenses work. Lenses are just pieces of glass (or other transparent materials) with one or two spherical surfaces that can focus or spread out light rays. This ability to bend light is what allows lenses to form images and is used in everything from eyeglasses to cameras to telescopes.

Terminology in Refraction from Spherical Surfaces

• Principal Axis: This is the straight line that passes through the centers of curvature of the spherical surfaces. It’s like the “spine” of the lens system, providing a reference line for measuring distances and angles.
• Pole (P): The pole is the point on the spherical surface that lies on the principal axis. It’s analogous to the “tip” of the lens where the principal axis touches the surface.
• Centre of Curvature (C): Imagine a full sphere from which your spherical surface is a part; the center of that sphere is the center of curvature. It’s not physically present in the lens but is important for understanding the lens’s curvature.
• The radius of Curvature (R): This is the radius of the imaginary sphere mentioned above. It determines how “curved” the surface is. A smaller radius means a more curved surface, and vice versa.
• Aperture: The aperture of a spherical surface is the actual clear opening through which light can pass. It’s like the “window” of the lens that determines how much light can go through.
• Optical Centre (O): For lenses, the optical centre is the point inside the lens where light rays passing through do not get deviated. It’s the “central point” of the lens.
• Focal Point (F): This is the point where parallel rays of light either converge or appear to diverge after passing through the lens. It’s the “focal spot” of the lens system.
• Focal Length (f): The distance between the optical centre and the focal point is the focal length. It tells us how strongly the lens converges or diverges light.

These terms form the basic vocabulary when discussing refraction through spherical surfaces. They help in understanding how light behaves as it passes through different mediums and surfaces, which is crucial for lens design and application in optical devices.

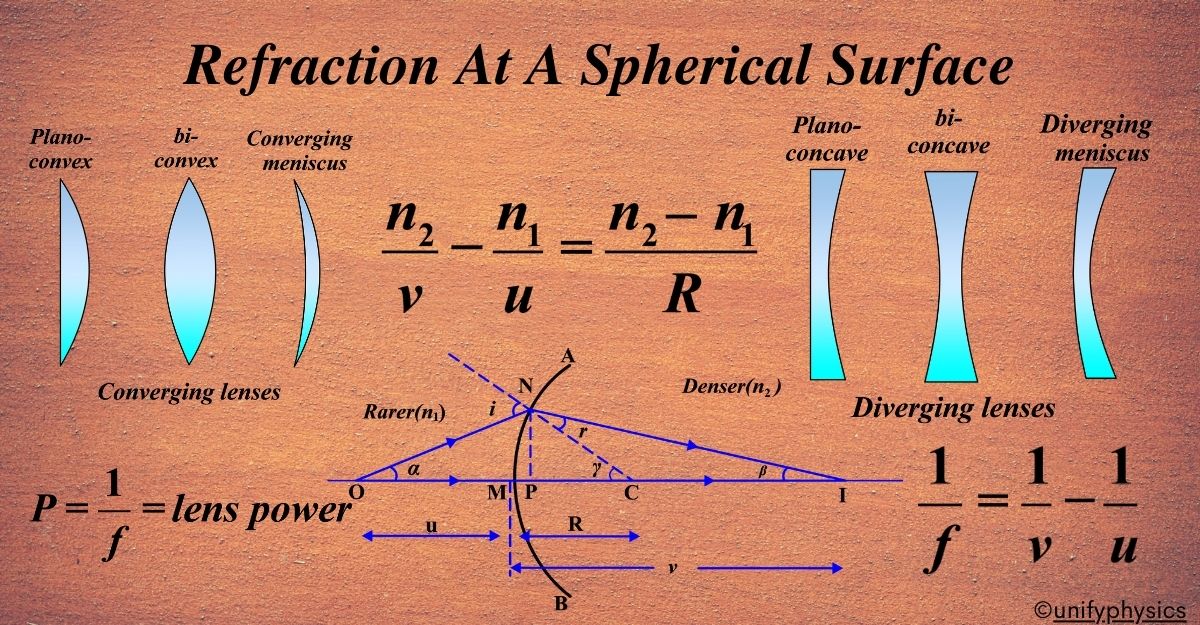
A diagram shows how an image is formed when light passes through a curved surface, like a part of a clear ball. This curved surface has a special point called the center of curvature ©, and the distance from this point to the surface is the radius of curvature ®. Light comes from an object (O) and travels through the air (which has a refractive index (n₁) into a different material like glass or water (with a refractive index (n₂).

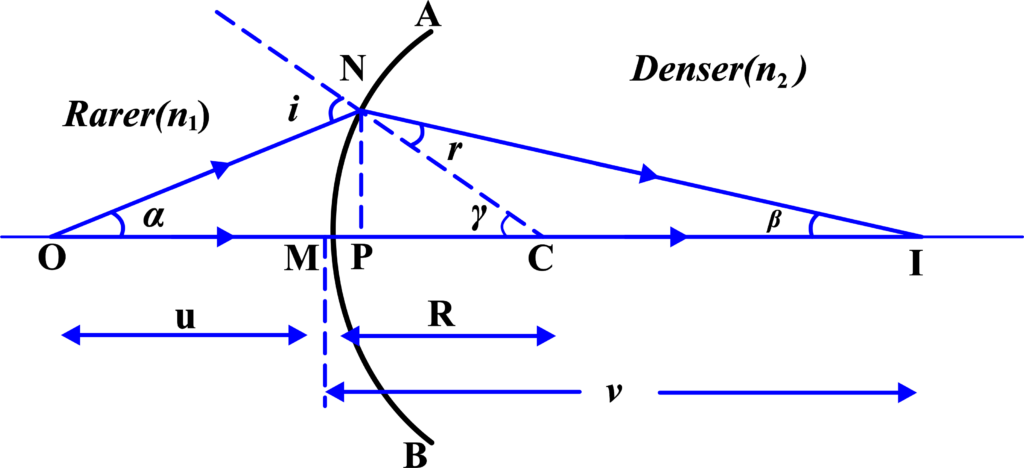
The diagram assumes that the curved surface isn’t too wide so that we can make some approximations for simplicity. Specifically, we can treat the distance from a point on the surface (N) to the principal axis (the straight line that runs through the center of curvature and the optical center of the surface) as almost the same as if we drew a line straight down from N to the axis.

For small angles, the tangent of the angle is approximately equal to the angle itself in radians. Hence,

\(\displaystyle\tan \angle NOM \approx \angle NOM = \frac{MN}{OM} \)

\(\displaystyle \tan \angle NCM \approx \angle NCM = \frac{MN}{MC} \)

\(\displaystyle\tan \angle NIM \approx \angle NIM = \frac{MN}{MI} \)

Considering ( \(\displaystyle\triangle NOC \)), the exterior angle ( i ) is the sum of the interior opposite angles:

\(\displaystyle i = \angle NOM + \angle NCM \)

Substituting the approximations,

\(\displaystyle i \approx \frac{MN}{OM} + \frac{MN}{MC} \)

Since ( OM = -u ) and ( MC = R ),

\(\displaystyle i \approx MN \left( \frac{-1}{u} + \frac{1}{R} \right) ; i \approx MN \left( \frac{-1}{u} + \frac{1}{R} \right) \)

Considering (\(\displaystyle \triangle NCI\) ), the exterior angle ( r ) is the sum of the interior opposite angles:

\(\displaystyle r = \angle NCM – \angle NIM \)

Substituting the approximations,

\(\displaystyle r \approx \frac{MN}{MC} – \frac{MN}{MI} \)

Since ( MC = R ) and ( MI = v ),

\(\displaystyle r \approx MN \left( \frac{1}{R} – \frac{1}{v} \right) \)

According to Snell’s law at the point of incidence ( N ), \(\displaystyle n_1 \sin i = n_2 \sin r \) Using the small angle approximation where (\(\displaystyle \sin \theta \approx \theta \)), \(\displaystyle n_1 i \approx n_2 r \) Substituting the expressions for ( i ) and ( r ),

\(\displaystyle n_1 \left( MN \left( \frac{-1}{u} + \frac{1}{R} \right) \right) = n_2 \left( MN \left( \frac{1}{R} – \frac{1}{v} \right) \right) \)

Simplifying, we get:

\(\displaystyle n_1 \left( \frac{-1}{u} + \frac{1}{R} \right) = n_2 \left( \frac{1}{R} – \frac{1}{v} \right) \)

Rearranging terms to isolate the variables ( u ), ( v ), and ( R ),

\(\displaystyle n_1 \left( \frac{-1}{u} + \frac{1}{R} \right) = n_2 \left( \frac{1}{R} – \frac{1}{v} \right) \)

Multiplying through by ( R ),

\(\displaystyle n_1 \left( \frac{R – u}{uR} \right) = n_2 \left( \frac{R – v}{vR} \right) \)

\(\displaystyle n_1 (R – u)v = n_2 (R – v)u\)

\(\displaystyle n_1 vR – n_1 uv = n_2 uR – n_2 uv \)

Bringing all terms involving ( uv ) to one side,

\(\displaystyle n_1 vR – n_1 uv + n_2 uv = n_2 uR \)

\(\displaystyle n_1 vR + (n_2 – n_1) uv = n_2 uR\)

Dividing through by ( uvR ),

\(\displaystyle \frac{n_1 v}{uvR} + \frac{(n_2 – n_1)}{v} = \frac{n_2 u}{uvR}\)

\(\displaystyle \frac{n_1}{u} – \frac{n_2}{v} = \frac{n_2 – n_1}{R} \)

The derived expression for refraction at a spherical surface is:

\(\displaystyle\begin{equation}\label{eqn:1}\boxed{\boldsymbol{\frac{n_1}{u} – \frac{n_2}{v} = \frac{n_2 – n_1}{R} }} \end{equation}\)

This equation relates the object distance (u), the image distance (v), the radius of curvature (R), and the refractive indices of the two media (n1) and (n2). It is fundamental to understanding how light behaves when transitioning between different media through a curved surface.

Types of Refraction from Spherical Surfaces

When we talk about refraction from spherical surfaces, we’re essentially discussing how light bends when it passes through a surface that’s part of a sphere. Two main types of refraction can occur on spherical surfaces, and they are based on the shape of the surface:

• Refraction at a Convex Spherical Surface: This occurs when the spherical surface bulges outwards, towards the incoming light. Imagine the outer surface of a round glass ball; that’s a convex spherical surface. When light rays hit this surface, they bend towards the normal (an imaginary line perpendicular to the surface at the point of contact). If the second medium is denser than the first, like going from air into glass, the light rays converge, or come together, at a point.
• Refraction at a Concave Spherical Surface: Now, picture the inside surface of a hollow glass ball. That’s a concave spherical surface, which curves inwards, away from the incoming light. When light rays strike this type of surface, they also bend towards the normal if they’re entering a denser medium. However, because of the surface’s shape, the light rays diverge, or spread out, after refraction.

These two types of refraction are fundamental in understanding how lenses work. Convex surfaces are used to make converging lenses, like those found in magnifying glasses, while concave surfaces are used for diverging lenses, like those used to correct for nearsightedness.

Assumptions in Refraction from Spherical Surfaces

• Small Aperture: We assume that the aperture (the actual opening through which light passes) of the spherical refracting surface is small. This simplification allows us to concentrate on the central region where most of the refraction occurs.
• Paraxial Rays: We consider only paraxial rays, which are rays close to the principal axis. These rays make small angles with the axis and are easier to analyze mathematically. By focusing on paraxial rays, we can approximate the behavior of all rays passing through the surface.
• Point Object: We assume that the object is a point object, meaning it is very small compared to the distances involved. This simplification helps us analyze the behavior of light rays without worrying about the object’s size or shape.
• Principal Axis Alignment: The object lies on the principal axis, which is the straight line passing through the centers of curvature of the spherical surfaces. Considering the principal axis simplifies our calculations and ensures symmetry in the system.

By making these assumptions, we can derive expressions and understand how light bends at spherical surfaces.

Types of Spherical Lenses

Spherical lenses are the workhorses of the optical world. These fundamental components are found in everything from eyeglasses to telescopes, and their design plays a crucial role in how they manipulate light. There are two main types of spherical lenses, each with unique properties that determine their function: convex and concave lenses. Understanding these different types is the first step to unlocking the fascinating world of spherical lenses and their countless applications.

Convex Lens (Converging Lens)

A convex lens is also known as a converging lens because it “converges” light rays that fall on it. The lens surface is convex in nature, meaning it bulges outward.

When a ray of light passes parallel to the principal axis of a convex lens, the refracted ray passes through the focus. If the incident ray passes through the optical center, the refracted ray does not deviate at all. When the incident ray passes through the focus of the convex lens, the refracted ray then passes parallel to the principal axis.

Imagine sunlight passing through a magnifying glass. The magnifying glass is a convex lens. The lens bends the sunlight, bringing it to a focus point, and creating a tiny, intense spot of light. This property of focusing light makes convex lenses useful in various applications.

Types of Convex Lenses:

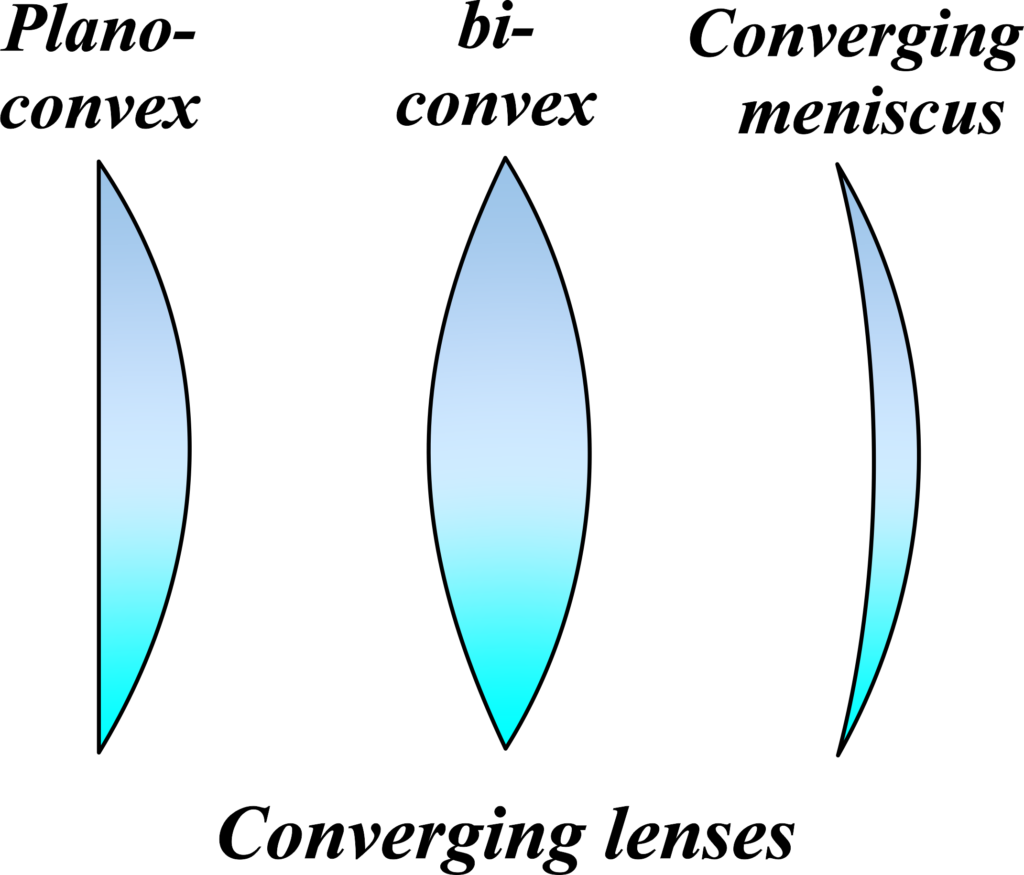
Bi-Convex Lens (Biconvex Lens): A bi-convex lens has both surfaces curved outward in a spherical shape. It looks like a thick, bulging disc. Bi-convex lenses are commonly used in various optical devices. They converge parallel light rays to a focus point.

Plano-Convex Lens: A plano-convex lens has one flat surface and one curved surface. The curved surface is convex (bulging outward). These lenses are thicker at the center and thinner at the edges. Plano-convex lenses are versatile and find applications in everyday life, including eyeglasses and magnifying glasses.

Concavo-Convex Lens (Meniscus Lens): A concavo-convex lens has one surface that is concave (curved inward) and one surface that is convex (curved outward). It resembles a lens with one side thicker than the other. Concavo-convex lenses are used to balance out spherical aberrations caused by other lenses. They are also used to control laser beams.

Concave Lens (Diverging Lens)

A concave lens is shaped such that it is thinner at the center than at the edges. It is also known as a diverging lens because it causes light rays to spread out or diverge when they pass through it.

The lens has at least one inwardly curved surface, resembling a cave. When parallel light rays enter a concave lens, they diverge on the other side, appearing to come from a common point called the virtual focus. Unlike convex lenses, which bend light rays towards each other, concave lenses bend light rays away from each other.

This divergence means that the light rays never actually meet, but instead, they seem to originate from a point on the same side of the lens as the light source. The point from which the divergent rays appear to originate is known as the virtual focus of the concave lens. This focus is not a point where the light rays converge, hence the term ‘virtual’.

Types of Concave Lenses:

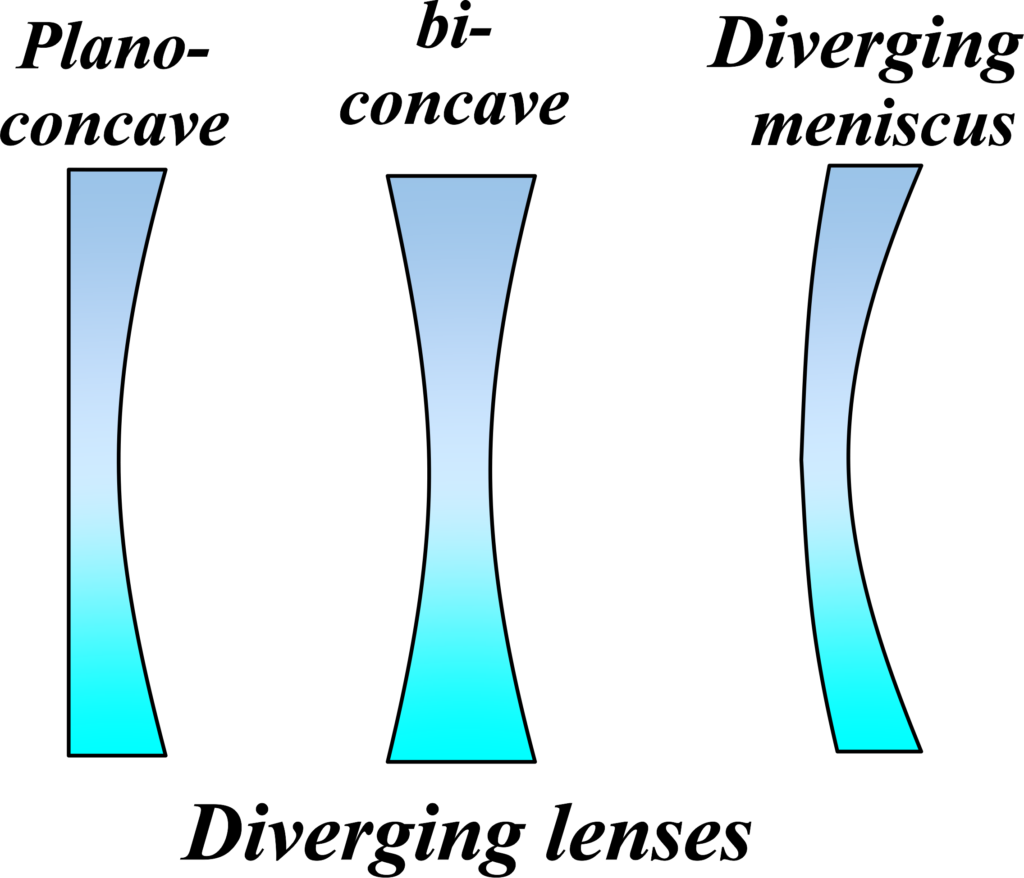
Biconcave Lens (Plano-Concave Lens): A biconcave lens has both surfaces curved inward in a spherical shape. It looks like a thin, hollowed-out disc. Biconcave lenses diverge light rays that fall on them. They are commonly used in optical devices where light needs to spread out or correct vision.

Plano-Concave Lens: A plano-concave lens has one flat surface and one curved surface. The curved surface is concave (curved inward). These lenses are thinner at the center and thicker at the edges. Plano-concave lenses are versatile and find applications in eyeglasses, projectors, and other optical systems.

Convexo-Concave Lens (Meniscus Lens): A convexo-concave lens has one surface that is convex (curved outward) and one surface that is concave (curved inward). It resembles a lens with one side thicker than the other. Convexo-concave lenses are used to balance out aberrations caused by other lenses. They find applications in telescopes, microscopes, and corrective eyewear.

Sign Convention for Spherical Lenses

When dealing with lenses, we need a consistent way to describe the direction and orientation of light rays, distances, and image characteristics. This is where sign conventions come in handy. We use the New Cartesian Sign Convention for spherical lenses, which is as follows:

• Optical Centre (O): All distances are measured from the optical center of the lens.
• Direction of Incident Light: Distances measured in the same direction as the incident light (towards the right) are considered positive. Distances measured against the direction of incident light (towards the left) are considered negative.
• Object Distance (u): Since the object is always placed to the left of the lens, the object distance (u) is always negative.
• Image Distance (v): If the image is formed on the right side of the lens (real image), the image distance (v) is positive. If the image is formed on the left side of the lens (virtual image), the image distance (v) is negative.
• Height of Object and Image (h): The heights measured above the principal axis are positive. Heights measured below the principal axis are negative.
• Focal Length (f): For a convex lens (converging lens), the focal length (f) is positive. For a concave lens (diverging lens), the focal length (f) is negative.

This sign convention helps us predict the nature and position of the image formed by spherical lenses.

Refraction By A Lens

When light travels through a lens, it undergoes refraction, which means it bends. This bending occurs because light changes speed when it moves from one medium to another—like from air into glass or plastic, which are common lens materials.

As light hits the lens, it first refracts at the front surface of the lens. It then travels through the lens material and refracts again at the back surface as it exits into the air.

Light slows down when it enters the lens because the lens material is denser than air. This causes the light to bend towards the normal—an imaginary line perpendicular to the surface at the point of entry. The light travels in a straight line inside the lens until it reaches the other side.

As the light exits the lens, it speeds up again because it’s moving into a less dense medium (air). This causes the light to bend away from the normal.

• Converging Lenses (Convex): These lenses are thicker in the middle and cause parallel light rays to converge at a point known as the focal point.
• Diverging Lenses (Concave): These lenses are thinner in the middle and cause parallel light rays to spread out or diverge.

The ability of lenses to bend light is what allows them to form images on our retinas, in cameras, and telescopes. It’s also how glasses correct vision—by refocusing light to the right spot.

Also Read: Reflection of Light by Spherical Mirrors

Image Formation by Lenses

Formation of Image by a Convex Lens: A convex lens can form real or virtual images depending on the object’s position relative to the focal point.

Formation of Image by a Concave Lens: A concave lens always forms virtual, upright, and reduced images.

This table outlines the behavior of a concave lens in terms of image formation. Concave lenses always produce virtual, upright, and diminished images regardless of the object’s position relative to the lens.

General Formula for Lens

The lens formula is a fundamental equation in optics that helps us understand how light behaves when passing through lenses. It relates the focal length (f), object distance (u), and image distance (v) for both convex and concave lenses. Here’s the formula:

\(\displaystyle \frac{1}{f} = \frac{1}{v} – \frac{1}{u} \)

When light passes through a lens, it bends due to refraction. The lens formula helps us predict where the image will form and its characteristics.

• If the image distance (v) is positive, the image is real and formed on the opposite side of the lens from the object.
• If the image distance (v) is negative, the image is virtual and formed on the same side as the object.
• The focal length (f) determines how strongly the lens converges or diverges light.

Magnification produced by Lenses

Magnification is the ratio of the height of the image to the height of the object and is given by the formula

\(\displaystyle m = \frac{v}{u} \)

Here, (v) is the image distance (the distance from the lens to the image), and (u) is the object distance (the distance from the lens to the object). It’s a way to determine how much larger or smaller the image is compared to the object, based on their distances from the lens.

If ( m > 1 ), the image is magnified (larger than the object).
If ( m < 1 ), the image is diminished (smaller than the object).
If ( m = 1 ), the image is the same size as the object.

A positive value of ( m ) indicates an upright (virtual) image while a negative value of ( m ) indicates an inverted (real) image. This concept is particularly useful when you want to calculate the magnification without directly measuring the size of the object and the image.

Power of a Lens

The power of a lens is a measure of its ability to bend light. In other words, it tells us how strong a lens is at converging (for convex lenses) or diverging (for concave lenses) light rays that pass through it. The power of a lens (P) is defined as the reciprocal of its focal length (f) in meters (m). The formula is:

\(\displaystyle P = \frac{1}{f} \)

The SI unit of the power of a lens is diopters (D), which is equivalent to ( m^-1 ) or one over meters. For a convex lens (which converges light), the power is positive and for a concave lens (which diverges light), the power is negative. A lens with a short focal length has a greater power because it bends light more sharply. Conversely, a lens with a long focal length has less power.

Power of Combined Lenses:

The combined power of lenses in contact is the algebraic sum of their individual powers. If you have two lenses with powers ( P₁ ) and ( P₂ ), the total power ( P ) of the combination is:

\(\displaystyle P = P_1 + P_2 \)

A convex lens has positive power, while a concave lens has negative power. When combining, you add the powers algebraically, taking into account their signs. The resultant power determines how the combined lenses will bend light. A higher positive power means a stronger converging ability, while a higher negative power means a stronger diverging ability.

Uses of a Concave and Convex Lens

Uses of a Concave Lens (Diverging Lens):

• Correcting Myopia: Concave lenses are used in eyeglasses to correct nearsightedness (myopia), allowing users to see distant objects more clearly.
• Camera Lenses: They are part of camera lenses, particularly in zoom lenses, to control the divergence of light and help focus.
• Peepholes: Concave lenses are used in door peepholes as they allow a wider field of view from inside to outside.
• Flashlights: In flashlights, these lenses spread out the light beam, providing a wider illumination area.

Uses of a Convex Lens (Converging Lens):

• Correcting Hypermetropia: Convex lenses are used in eyeglasses to correct farsightedness (hypermetropia), enabling users to see nearby objects more clearly.
• Magnifying Glasses: They are used in magnifying glasses to enlarge the appearance of objects when viewed through them.
• Microscopes: Convex lenses are essential in microscopes, where they are used to magnify small objects or details that are not visible to the naked eye.
• Projectors: In projectors, convex lenses are used to focus light and create clear images on a screen.
• Telescopes: They are a critical component of telescopes, allowing us to see distant celestial objects by converging light to form a clear image.

Solved Examples

Example 1: A convex spherical surface with a radius of curvature of 10 cm separates two media with refractive indices ( n₁ = 1.5 ) (glass) and ( n₂ = 1.0 ) (air). An object is placed 20 cm from the surface in the glass medium. Calculate the position of the image formed.

Solution: We use the refraction formula at a spherical surface:

\(\displaystyle\frac{n_2}{v} – \frac{n_1}{u} = \frac{n_2 – n_1}{R}\)

Given: n₁ = 1.5 ; n₂ = 1.0 ; u = -20 cm (object distance, negative since it is on the same side as the incoming light); R = 10 cm (positive for convex surface)

Substitute the values:

\(\displaystyle\frac{1.0}{v} – \frac{1.5}{-20} = \frac{1.0 – 1.5}{10}\)
\(\displaystyle\frac{1.0}{v} + \frac{1.5}{20} = \frac{-0.5}{10}\)
\(\displaystyle\frac{1.0}{v} + 0.075 = -0.05\)
\(\displaystyle\frac{1.0}{v} = -0.05 – 0.075\)
\(\displaystyle\frac{1.0}{v} = -0.125\)
\(\displaystyle v = -8 \text{ cm}\)

The image is formed 8 cm on the same side of the surface as the object, indicating a virtual image.

Example 2: An object is placed 15 cm from a convex lens with a focal length of 10 cm. Determine the position and nature of the image formed.

Solution: We use the lens formula:

\(\displaystyle\frac{1}{f} = \frac{1}{v} – \frac{1}{u}\)

Given: f = 10 cm (positive for convex lens); u = -15 cm (object distance, negative since the object is on the opposite side of the light)

Substitute the values:

\(\displaystyle\frac{1}{10} = \frac{1}{v} + \frac{1}{15}\)
\(\displaystyle\frac{1}{v} = \frac{1}{10} – \frac{1}{15}\)
\(\displaystyle\frac{1}{v} = \frac{3 – 2}{30}\)
\(\displaystyle\frac{1}{v} = \frac{1}{30}\)
\(\displaystyle v = 30 \text{ cm}\)

The image is formed 30 cm on the opposite side of the lens, indicating a real, inverted, and magnified image.

Example 3: An object is placed 20 cm from a concave lens with a focal length of -15 cm. Determine the position and nature of the image formed.

Solution: We use the lens formula:

\(\displaystyle\frac{1}{f} = \frac{1}{v} – \frac{1}{u}\)

Given: f = -15 cm (negative for concave lens); u = -20 cm (object distance, negative since the object is on the opposite side of the light)

Substitute the values:

\(\displaystyle\frac{1}{-15} = \frac{1}{v} + \frac{1}{20}\)
\(\displaystyle\frac{1}{v} = \frac{1}{-15} – \frac{1}{20}\)
\(\displaystyle\frac{1}{v} = \frac{-4 – 3}{60}\)
\(\displaystyle\frac{1}{v} = \frac{-7}{60}\)
\(\displaystyle v = -\frac{60}{7} \approx -8.57 \text{ cm}\)

The image is formed approximately 8.57 cm on the same side of the lens as the object, indicating a virtual, upright, and reduced image.

Example 4: An object 5 cm high is placed 30 cm from a convex lens of focal length 20 cm. Calculate the height of the image.

Solution: First, find the image distance using the lens formula:

\(\displaystyle\frac{1}{f} = \frac{1}{v} – \frac{1}{u}\)

Given: f = 20 cm; u = -30 cm

Substitute the values:

\(\displaystyle\frac{1}{20} = \frac{1}{v} – \frac{1}{-30}\)
\(\displaystyle\frac{1}{v} = \frac{1}{20} + \frac{1}{30}\)
\(\displaystyle\frac{1}{v} = \frac{3 + 2}{60}\)
\(\displaystyle\frac{1}{v} = \frac{5}{60}\)
\(\displaystyle v = 12 \text{ cm}\)

Next, calculate the magnification (m):

\(\displaystyle m = \frac{v}{u} = \frac{12}{-30} = -0.4\)

Finally, calculate the height of the image (h_i):

\(\displaystyle h_i = m \times h_o = -0.4 \times 5 \text{ cm} = -2 \text{ cm}\)

The height of the image is -2 cm, indicating the image is inverted and reduced.

Example 5: Calculate the power of a convex lens with a focal length of 25 cm.

Solution: The power (P) of a lens is given by:

\(\displaystyle P = \frac{1}{f}\)

Given: f = 25 cm = 0.25 m (convert to meters)

Substitute the values:

\(\displaystyle P = \frac{1}{0.25} = 4 \text{ diopters}\)

The power of the lens is 4 diopters.

Example 6: A concave lens forms an image 10 cm from the lens when an object is placed 30 cm from the lens. Calculate the focal length and power of the lens.

Solution: We use the lens formula:

\(\displaystyle\frac{1}{f} = \frac{1}{v} – \frac{1}{u}\)

Given: u = -30 cm; v = -10 ) cm (negative for a virtual image on the same side as the object)

Substitute the values:

\(\displaystyle\frac{1}{f} = \frac{1}{-10} – \frac{1}{-30}\)
\(\displaystyle\frac{1}{f} = \frac{-3 + 1}{30}\)
\(\displaystyle\frac{1}{f} = \frac{-2}{30}\)
\(\displaystyle f = -15 \text{ cm} = -0.15 \text{ m}\)

Next, calculate the power (P):

\(\displaystyle P = \frac{1}{f} = \frac{1}{-0.15} \approx -6.67 \text{ diopters}\)

The focal length of the concave lens is -15 cm, and the power of the lens is -6.67 diopters.

FAQs