In the 17th century, light was a mystery. Some thought it was made of particles, while others believed it was a wave. Enter Christiaan Huygens, a Dutch scientist passionate about understanding the natural world. In 1678, Huygens proposed a radical idea that would change the way we see light forever.
Huygens suggested that light could be understood as waves spreading out from a source, much like ripples in a pond. He imagined that every point on a wavefront could be considered a new source of wavelets, expanding in every direction. This idea was groundbreaking because it provided a simple yet powerful way to predict how light waves move and interact with objects.
Huygens’ initial ideas were just the beginning. He used this principle to explain how light waves could bend (refract) when entering a new medium and how they could bounce back (reflect) from surfaces. His principle was simple: every wavefront point is the source of new spherical waves.
Later, in the 19th century, a French engineer named Augustin-Jean Fresnel would take Huygens’ Principle further. Fresnel combined Huygens’ ideas with his studies on wave interference to explain more complex phenomena like the bending of light around obstacles (diffraction).
Today, Huygens’ Principle is more than just a historical footnote. It’s a fundamental concept in physics that helps us understand light and other types of waves. It’s used in designing optical instruments and even in understanding the nature of quantum mechanics.
What is Huygens’ Principle?
Huygens’ Principle states that every point on a wavefront acts as a source of tiny, secondary wavelets that spread out in all directions at the same speed as the wave itself. Imagine you’re at a calm lake and you drop a single pebble into the water. You see ripples forming and spreading out in circles from where the pebble fell. Now, picture that every point along the edge of those ripples starts to create its own set of ripples. This is similar to Huygens’ Principle about waves.
Huygens’ Principle states that every point on a wavefront (like the edge of those ripples) is the source of secondary wavelets that spread out in all directions at the same speed as the original wave. These secondary wavelets add up to form a new wavefront.
In simpler terms, if you have a wave moving through space, you can predict where the wave will be in the future by looking at where the wavelets from each point on the wavefront will travel. This principle helps us understand how waves like light and sound move and interact with things around them.
Each point on the wavefront has its own set of pebbles, creating new ripples that join together to push the wave forward. This idea helps us predict how waves behave when they hit barriers, pass through openings, or move from one medium to another.
What are Wavefronts?
Wavefronts are like the wave’s leading edge, marking the boundary of the wave’s reach at any given moment. They help us map out the wave’s journey through space and time. Imagine you’re at a concert, and the speakers start playing your favorite song. The music spreads out through the air, reaching everyone in the crowd. Now, if we could freeze a moment and trace a line connecting all the points where the sound is the loudest (like when the beat drops), that line would be a wavefront.
In physics, a wavefront is an imaginary surface representing all the points of a wave that are in sync. It’s like taking a snapshot of the wave in one instant and seeing where all the high points (crests) or low points (troughs) line up. These points are all experiencing the same part of the wave’s cycle—they’re all at the peak of the wave, or all in the valley, at the same time.
So, a wavefront is a way to visualize how a wave moves through space. It’s not something you can touch or see, but it’s a really useful concept for understanding waves better. It helps us predict where the wave will go next and how it will behave when it encounters obstacles or moves from one medium to another.
Types of Wavefronts
Think of a wave in the ocean. It can have different shapes depending on where it comes from and what it encounters. Similarly, when we talk about waves like light or sound, we describe their shape at a particular moment using the idea of wavefronts. Three main types of wavefronts describe the shape of a wave at any given point in time:
Plane Wavefronts:
When we talk about Plane Wavefronts, we’re describing a type of wavefront that is flat and extends in straight lines. These wavefronts are typically produced by light sources that are very far away from us, like stars in the night sky.
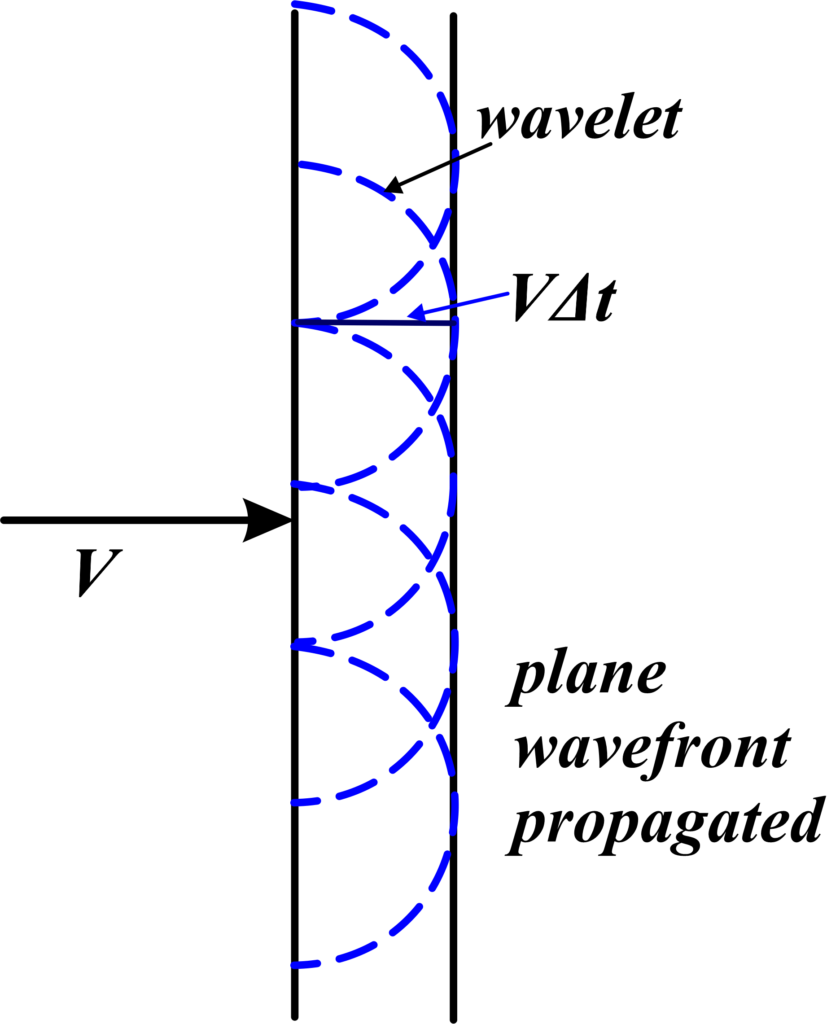
- Uniformity: Plane wavefronts are uniform and even, meaning that the wave’s intensity doesn’t change across the wavefront.
- Parallel Rays: The light rays that come from a plane wavefront are parallel to each other. This is because the source of the wavefront is so far away that, by the time the light reaches us, it’s traveling in straight, parallel lines.
- No Curvature: Unlike spherical wavefronts that curve outward from a central point, plane wavefronts have no curvature. They’re like a perfectly flat sheet of paper.
Plane Wavefronts are a simplified model that we use in physics to describe how waves behave when they travel large distances. Example: A very distant lighthouse seen from the shore. The light rays coming from the lighthouse are so far away that they appear parallel by the time they reach the observer. This creates plane wavefronts, which are essentially flat and extend straight across.
Spherical Wavefronts:
When we talk about Spherical Wavefronts, we’re picturing a wave that spreads out in all directions from a single point source. This is similar to what happens when you drop a stone into a still pond and watch the ripples move outward.

- Origin: They originate from a point source, like a small light bulb or the tip of a pen when you tap it on water.
- Shape: As the name suggests, they form a sphere, expanding equally in all directions.
- Energy Distribution: The energy of the wave spreads out as it travels, so the intensity decreases with distance.
Example: A pebble is thrown into a still pond. The ripples created by the pebble spread out in all directions from the point of impact. Each ripple represents a spherical wavefront, expanding outward in a sphere-like shape.
In the context of light, a spherical wavefront would mean that the light is emanating from a point and illuminating in a spherical shape. These spread out from a point source, like the ripples from where a pebble drops into the water. Picture a balloon inflating. Every point on the surface of the balloon is part of a spherical wavefront.
Cylindrical Wavefronts:
Cylindrical wavefronts are a type of wavefront that emerges when the source of the wave is a line rather than a point. This line source creates waves that spread out in a shape that resembles a cylinder.
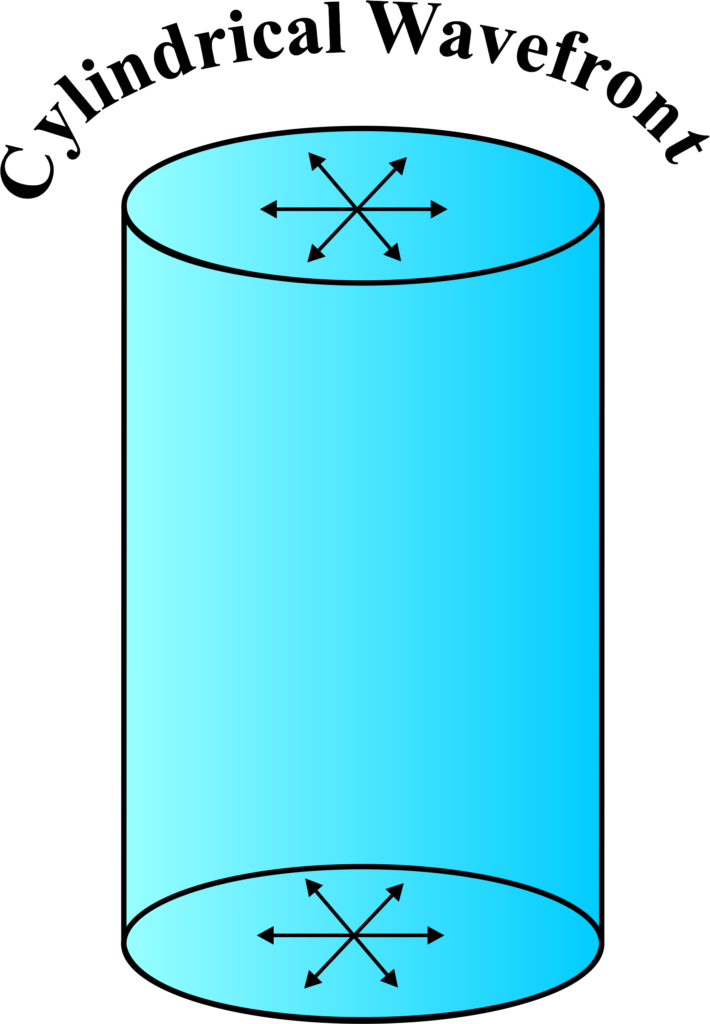
- Line Source: The source of a cylindrical wavefront is extended in one dimension, like a long string or a tube light.
- Shape: The wavefront takes the form of a cylinder. If you could see the wavefront, it would look like a series of circles that are all centered around the line source, creating a cylinder shape as they expand.
- Propagation: The waves move outward perpendicular to the line source, maintaining the cylindrical shape as they travel.
Example: Sound from a long, straight flute. As the musician plays, the sound waves travel outwards from the flute. These waves form cylindrical wavefronts, spreading out in circles around the line of the flute.
In the context of light, if you have a long, narrow slit that light is passing through, the light waves that come out of that slit will form cylindrical wavefronts. These wavefronts are useful in understanding how light behaves in certain optical setups, like lasers or slit experiments.
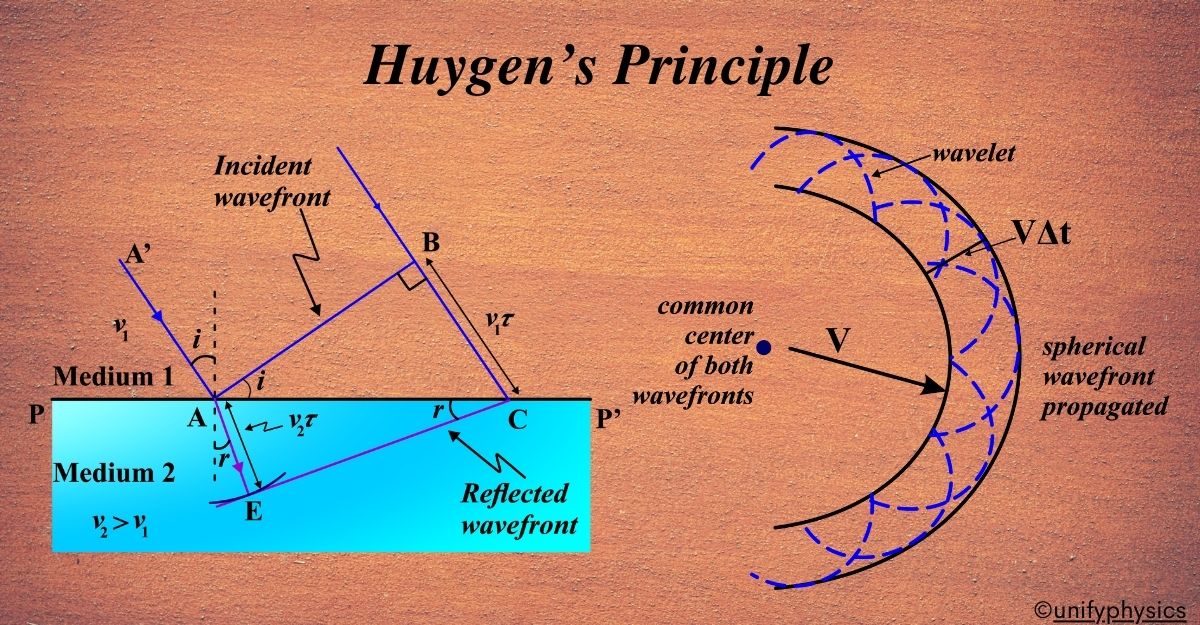
Reflection of Plane Waves using Huygens Principle
When plane waves reflect off a surface, each point on the wavefront acts as a source of new wavelets. The reflected wavefront is the envelope of these wavelets, maintaining the angle of incidence equal to the angle of reflection. Now, Huygens’ Principle helps us understand exactly how this reflection happens. According to the principle:
- Every point on the incoming wavefront (the flat wave hitting the mirror) acts as a source of new tiny waves, called wavelets.
- These wavelets spread out in all directions, but because they’re on a reflective surface, they start to overlap and interfere with each other.
- The new wavefront, which is the reflected wave, is formed by drawing a line that’s tangent to all these overlapping wavelets.
Huygens’ Principle also confirms the laws of reflection, which state:
- The angle at which the wavefront hits the surface (angle of incidence) is equal to the angle at which it bounces off (angle of reflection).
- The incident wavefront, the reflected wavefront, and the normal (an imaginary line perpendicular to the surface) all lie in the same plane.
Let’s imagine a plane wave AB hitting a reflective surface MN at an angle denoted as ‘i’. The wave’s speed in the medium is represented by ‘v’, and ‘τ’ is the time it takes for the wavefront to move from point B to C. Therefore, the distance BC can be calculated as the product of ‘v’ and ‘τ’ (BC = vτ).
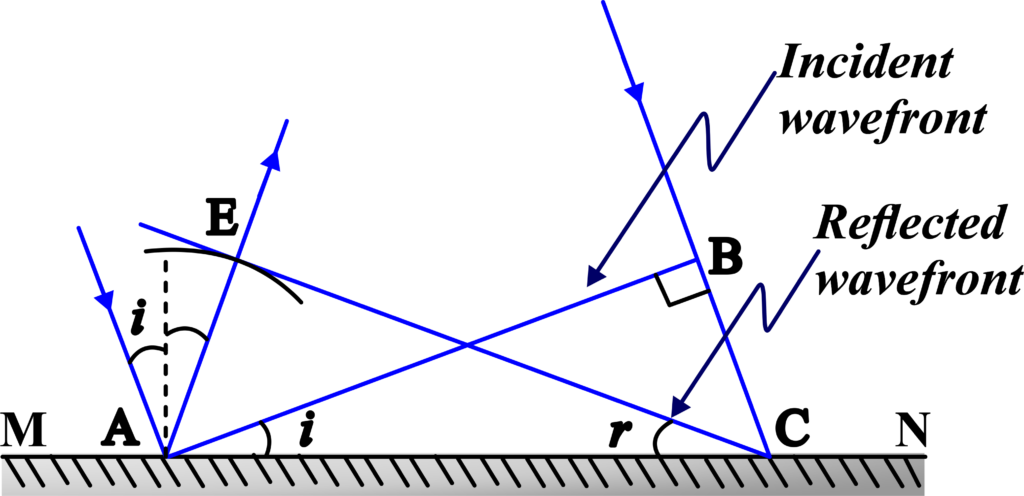
To illustrate the reflected wavefront, we draw a sphere with a radius of vτ from point A. The tangent plane drawn from point C to this sphere is represented by CE. AE equals BC, which is also vτ.
Upon examining triangles EAC and BAC, we find that they are congruent. As a result, the angles ‘i’ and ‘r’ are equal. This equality is known as the law of reflection. This concept is fundamental in understanding how waves behave upon hitting a reflective surface.
So, using Huygens’ Principle, we can not only visualize but also mathematically prove why the reflection of plane waves behaves the way it does. It’s like each point on the mirror is sending out its signal, and the combination of all these signals gives us the reflected wave that follows the laws of reflection.
Refraction of Plane Waves using Huygens Principle
As waves pass from one medium to another, the speed changes, causing the wavefronts to bend. This bending is refraction, and Huygens’ Principle helps us visualize how each point on the wavefront slows down or speeds up, leading to the bending effect.
Refraction is what happens when a wave, like a light wave, passes from one medium into another and changes direction. It’s like when you put a straw in a glass of water and it looks like it bends at the surface of the water. Huygens’ Principle helps us understand this “bending” by suggesting that:
- Every point on the wavefront (the front of the wave) in the first medium acts as a source of new wavelets.
- These wavelets spread out into the second medium at a speed that depends on the medium. If the second medium is denser, like going from air into water, the wavelets move slower.
- The new wavefront is formed by drawing a line that’s tangent to all these slower-moving wavelets.
For plane waves, which are flat and extend straight across:
- When they hit the boundary between two media, each point on the wavefront starts creating these slower-moving wavelets.
- Because the wavelets on one side of the wavefront enter the new medium first, they start slowing down before the wavelets on the other side.
- This causes the whole wavefront to tilt and change direction, which is the refraction we see.
Imagine two different materials, medium 1 and medium 2, separated by a boundary line (PP’). Light travels at different speeds in these two mediums, v1 and v2 respectively.
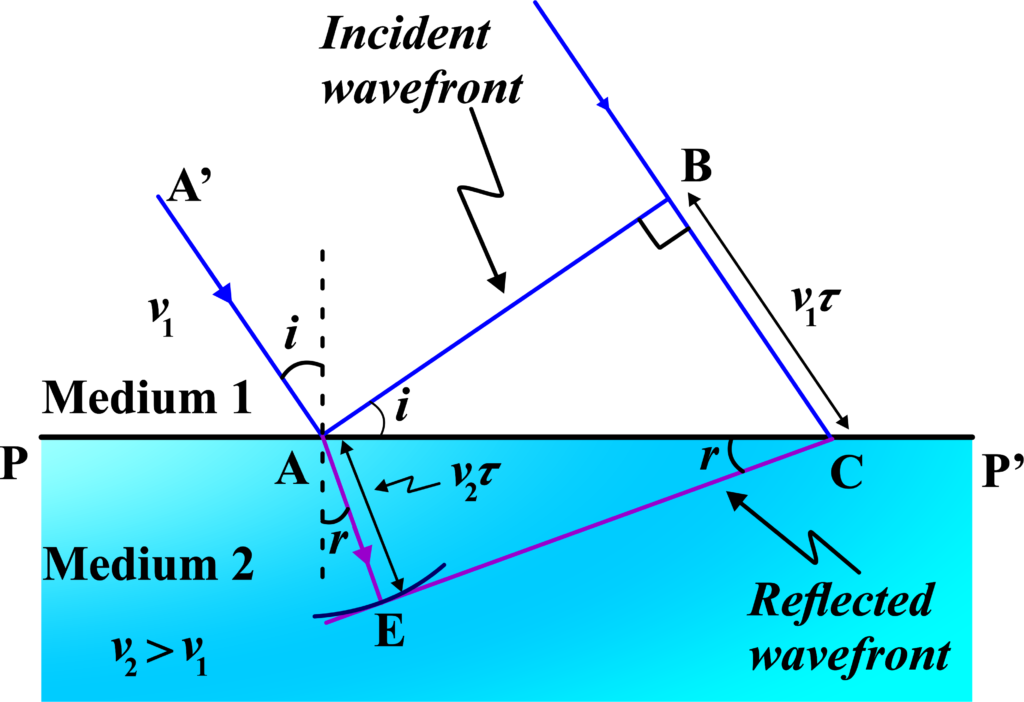
Now, consider a plane wavefront AB moving from medium 1 to medium 2, hitting the boundary at an angle i. The wavefront takes time τ to travel distance BC, so we can say BC equals v1 times τ.
To find out what happens to the wavefront after it enters medium 2, we imagine a sphere spreading out from point A with a radius of v2 times τ. The tangent plane CE drawn from point C to this sphere represents the refracted wavefront in medium 2.
By comparing triangles ABC and AEC, we find that the ratio of the sine of the incidence angle (i) to the sine of the refraction angle ® equals the ratio of v1 to v2. This tells us that if the light bends more towards the normal (r < i), it’s moving slower in medium 2 than in medium 1.
This prediction, which contradicts the corpuscular model of light, has been confirmed by experiments. If we denote the speed of light in vacuum as c, we can define the refractive indices of medium 1 and medium 2 as n1 = c/v1 and n2 = c/v2 respectively. This leads us to Snell’s law of refraction: n1 times sine of i equals n2 times sine of r.
Finally, if we denote the wavelengths of light in medium 1 and medium 2 as λ1 and λ2 respectively, we find that when a wave is refracted into a denser medium (where v1 > v2), both the wavelength and speed of propagation decrease, but the frequency (ν = v/λ) remains the same.
So, Huygens’ Principle gives us a way to visualize and calculate how and why plane waves change direction when they move from one medium to another. It’s a bit like a marching band having to slow down and change direction as they move from the pavement onto the sand.
Law of Refraction using Huygens’ Principle
The Law of Refraction, also known as Snell’s Law, tells us how a ray of light bends when it passes from one medium into another. It says that the ratio of the sine of the angle of incidence (the angle at which the light hits the boundary) to the sine of the angle of refraction (the angle at which the light bends) is constant and is equal to the ratio of the speeds of light in the two media.
Huygens’ Principle and Refraction: Huygens’ Principle helps us visualize this law by considering every point on a wavefront as a source of new wavelets. Here’s how it works:
- When a plane wavefront reaches the boundary between two media, each point on the wavefront acts as a source of new wavelets.
- These wavelets spread out into the second medium at a speed that depends on that medium. If the second medium is denser, the wavelets move slower.
- The new wavefront is formed by drawing a line that’s tangent to all these wavelets.
Using Huygens’ Principle, we can derive the mathematical form of Snell’s Law. If (v1) is the speed of light in the first medium and (v2) is the speed of light in the second medium, and (θ1) and (θ2) are the angles of incidence and refraction, respectively, then Snell’s Law can be expressed as:
\(\displaystyle \frac{\sin \theta_1}{\sin \theta_2} = \frac{v_1}{v_2} \)
This equation shows that the change in the speed of light between the two media causes the light to bend, and the amount of bending can be calculated using the angles and the speeds of light in the two media.
Huygens Principle and Diffraction
Diffraction occurs when waves bend around obstacles. It results in the bending and spreading of waves as they pass around corners or through openings. Huygens’ Principle describes this by showing how wavelets from different parts of the wavefront interfere to form the new wavefront beyond the obstacle.
- According to Huygens’ Principle, every point on a wavefront can be thought of as a source of new, tiny waves called wavelets.
- When a wavefront encounters an obstacle with a small opening (like a narrow slit), the points on the wavefront that are not blocked by the obstacle become sources of these new wavelets.
- These wavelets spread out as they move forward, and when they pass through the slit, they begin to spread out in semicircles from each point of the wavefront within the slit.
- The spreading out of these wavelets beyond the slit is what we observe as diffraction. The waves are bending around the edges of the slit and interfering with each other, creating a pattern of spreading and overlapping waves.
Huygens’ Principle helps us understand how and why waves don’t just stop or reflect when they hit an obstacle but instead, find a way around it, bending and spreading out in new directions. This principle is key to explaining the behavior of waves in various diffraction scenarios, which is a fundamental concept in wave optics.
Advantages and Disadvantages of Huygens Principle
Advantages:
- Huygens’ Principle provides a clear and intuitive way to understand how waves move through space. It’s like having a map that shows you exactly how a wave travels from one point to another.
- This principle allows us to analyze how waves bend around obstacles or pass through slits, creating patterns that we can study and predict.
- It simplifies the explanation of why waves bend when they enter a different medium, such as light bending when it goes from air into water.
- With Huygens’ Principle, we can construct new wavefronts easily, which helps in understanding complex wave behaviors and designing experiments.
These advantages show how Huygens’ Principle is not just a theory but a practical tool that helps us make sense of the wave-like nature of light and sound. It’s like having a guidebook that explains the ‘why’ and ‘how’ of waves’ journeys through different environments.
Disadvantages:
- Huygens’ Principle doesn’t fully explain all aspects of light, such as how light is emitted, absorbed, or how it becomes polarized.
- The principle fails to account for the photoelectric effect, where light can cause the emission of electrons from a material.
- Huygens’ original theory assumed the existence of a medium called ‘luminiferous ether’ for light to propagate through. This concept was later disproven.
These disadvantages highlight that while Huygens’ Principle is useful, it doesn’t cover every phenomenon related to light and waves. It’s a bit like having a map that shows many roads but not all the alleys and shortcuts.
Also Read: Refraction At A Spherical Surface
Huygens Principle Applications
Huygens’ Principle isn’t just a theory; it’s a practical tool that scientists and engineers use in many different fields. Here are some of the ways it’s applied:
Optics:
- Designing Lenses: By understanding how light waves propagate, we can design lenses that focus light exactly where we want it, like in glasses or cameras.
- Telescopes & Microscopes: It helps us make telescopes that can see distant stars and microscopes that can see tiny cells.
Acoustics:
- Sound Engineering: In concert halls and theaters, understanding how sound waves spread out helps us design spaces where everyone can hear music or speech.
Wave Propagation:
- Radio & TV Signals: Huygens’ Principle explains how these waves travel, which is essential for broadcasting signals over long distances.
Understanding Nature:
- Earthquakes: Seismologists use it to understand how seismic waves travel through the Earth, which can help predict the impact of earthquakes.
Medical Imaging:
- Ultrasound: This principle is used in medical imaging to create pictures of babies in the womb or to look inside the body without surgery.
Quantum Physics:
- Particle Behavior: It even helps physicists predict how tiny particles like electrons will behave, which is important for developing new technologies.
Huygens’ Principle is like a Swiss Army knife for scientists—it has a lot of different uses, all of which help us understand and shape the world around us.
Solved Examples
Example 1: Explain Huygens’ Principle and describe how it can be used to determine the wavefronts of a propagating wave.
Solution: Huygens’ Principle states that every point on a wavefront serves as a source of secondary spherical wavelets, which spread out in all directions with a speed equal to the speed of propagation of the wave. The new wavefront at any subsequent time is the envelope of these secondary wavelets.
To use Huygens’ Principle to determine the wavefronts of a propagating wave, follow these steps:
1. Identify the Initial Wavefront: Consider the initial position of the wavefront at time (t).
2. Construct Secondary Wavelets: From every point on the initial wavefront, construct secondary spherical wavelets with a radius proportional to the speed of the wave and the time interval (∆t).
3. Draw the New Wavefront: The new wavefront at a time ( t + ∆ t ) is the surface tangent to all the secondary wavelets.
Huygens’ Principle helps determine the wavefronts of a propagating wave by treating each point on the wavefront as a source of secondary wavelets and drawing a new wavefront as the tangent to these wavelets.
Example 2: Using Huygens’ Principle, derive the law of reflection for plane waves incident on a plane surface.
Solution: Consider a plane wavefront (AB) incident on a reflecting surface at an angle (i).
1. Incident Wavefront: Let \( AB \) be the incident wavefront, and it makes an angle (i) with the reflecting surface.
2. Secondary Wavelets: According to Huygens’ Principle, each point on (AB) acts as a source of secondary wavelets.
3. Reflected Wavefront: To find the position of the new wavefront after reflection, consider the wavelets emanating from points (A) and (B). These wavelets will form a new wavefront (CD) such that the angle of reflection (r) is equal to the angle of incidence (i).
To prove this geometrically, consider:
– (A) is a point on the incident wavefront.
– (B) is another point on the wavefront at a distance (λ) (wavelength) apart.
– (C) and (D) are points where the wavelets meet to form the new wavefront after reflection.
Since the distance (AB) and (CD) are equal (equal wavelengths), the angles (i) and (r) are equal, leading to the law of reflection: i = r
Using Huygens’ Principle, the law of reflection for plane waves is derived by constructing secondary wavelets and finding the new wavefront, showing that the angle of incidence equals the angle of reflection (i = r).
Example 3: Using Huygens’ Principle, derive Snell’s law of refraction for plane waves passing from one medium to another.
Solution: Consider a plane wavefront (AB) incident at an angle (i) on the boundary separating two media with refractive indices (n1) and (n2).
1. Incident Wavefront: Let (AB) be the incident wavefront making an angle (i) with the normal to the surface.
2. Secondary Wavelets in Medium 2: According to Huygens’ Principle, each point on (AB) acts as a source of secondary wavelets in the second medium. The speed of the wave in the second medium is
\(\displaystyle v_{2} = \frac{c}{n_{2}} \)
3. Refracted Wavefront: To find the position of the new wavefront after refraction, consider the wavelets emanating from points (A) and (B).
Let (BC) be the distance traveled by the wavefront in the second medium in time (t), such that:
\(\displaystyle BC = v_2 t\)
In the first medium, the distance (AD) traveled by the wavefront in the same time \(t) is:
\(\displaystyle AD = v_1 t\)
Using the geometry of the wavefronts:
\(\displaystyle\frac{\sin i}{\sin r} = \frac{AD}{BC} = \frac{v_1}{v_2}\)
Since the speed of light in a medium is inversely proportional to the refractive index, we have:
\(\displaystyle\frac{v_1}{v_2} = \frac{n_2}{n_1}\)
Thus, Snell’s law is:
\(\displaystyle n_1 \sin i = n_2 \sin r\)
Using Huygens’ Principle, Snell’s law of refraction is derived by constructing secondary wavelets and finding the new wavefront, showing that (\(\displaystyle n_1 \sin i = n_2 \sin r \)).
Example 4: A plane wave of light is incident normally on a glass slab with thickness (d) and refractive index (n). Calculate the time taken for the light to travel through the slab using Huygens’ Principle.
Solution: When light is incident normally on a slab, it travels straight through without bending.
1. Speed of Light in Glass: The speed of light in the glass slab is ( \(\displaystyle v = \frac{c}{n} \)), where \( c \) is the speed of light in a vacuum.
2. Time Calculation: The time \( t \) taken to travel through the slab is given by:
\(\displaystyle t = \frac{d}{v}\)
Substitute \( v \) with (\(\displaystyle \frac{c}{n} \)):
\(\displaystyle t = \frac{d}{\frac{c}{n}} = \frac{dn}{c}\)
The time taken for the light to travel through the glass slab is (\(\displaystyle \frac{dn}{c} \)).
Example 5: A plane wavefront is incident at an angle of 30° on a plane mirror. Using Huygens’ Principle, determine the angle between the incident and reflected wavefronts.
Solution: According to the law of reflection, the angle of incidence is equal to the angle of reflection.
1. Angle of Incidence: ( i = 30°)
2. Angle of Reflection: ( r = 30°)
3. Total Angle Between Wavefronts: The total angle between the incident and reflected wavefronts is twice the angle of incidence (since the angles are equal and symmetric about the normal).
\(\displaystyle\text{Total angle} = 2i = 2 \times 30° = 60°\)
The angle between the incident and reflected wavefronts is 60°.
Example 6: A plane wavefront is incident at an angle of 45° on a water surface (refractive index ( n = 1.33). Using Huygens’ Principle, calculate the angle of refraction.
Solution: Using Snell’s law:
\(\displaystyle n_1 \sin i = n_2 \sin r\)
Where: ( n1 = 1) (air); ( i = 45°); ( n2 = 1.33)
Substitute the values:
\(\displaystyle 1 \times \sin 45° = 1.33 \sin r\)
\(\displaystyle\frac{\sqrt{2}}{2} = 1.33 \sin r\)
\(\displaystyle\sin r = \frac{\sqrt{2}}{2 \times 1.33} = \frac{1}{\sqrt{2} \times 1.33} \approx 0.53\)
\(\displaystyle r = \arcsin(0.53) \approx 32.1°\)
The angle of refraction is approximately 32.1°.
FAQs
What is Huygens’ Principle and how does it explain wave propagation?
Huygens’ Principle states that every point on a wavefront acts as a source of secondary spherical wavelets, which spread out in all directions at the same speed as the original wave. The new wavefront is the envelope of these secondary wavelets. This principle helps explain how waves propagate through space, bend around obstacles, and interact with each other.
How does Huygens’ Principle apply to the reflection of plane waves?
Huygens’ Principle applies to the reflection of plane waves by considering each point on the incident wavefront as a source of secondary wavelets. When these wavelets strike a reflective surface, they generate new wavelets that propagate back into the original medium. The new wavefront formed by these secondary wavelets represents the reflected wave, following the law of reflection.
How does Huygens’ Principle explain the refraction of plane waves?
Huygens’ Principle explains the refraction of plane waves by considering the wavefronts as they pass from one medium to another with a different refractive index. Each point on the incident wavefront generates secondary wavelets that travel at different speeds in the two media. The new wavefront, formed by the secondary wavelets, bends at the interface according to Snell’s law, representing the refracted wave.
What is the significance of secondary wavelets in Huygens’ Principle?
The significance of secondary wavelets in Huygens’ Principle lies in their ability to explain various wave behaviors, such as diffraction, reflection, and refraction. By considering each point on a wavefront as a source of these wavelets, Huygens’ Principle provides a unified way to understand how waves propagate, bend around obstacles, and change direction at interfaces.
How does Huygens’ Principle help in understanding wavefronts and their propagation?
Huygens’ Principle helps in understanding wavefronts and their propagation by illustrating how each point on a wavefront acts as a source of new wavelets. This concept allows us to visualize and predict the movement and evolution of wavefronts as they travel through different media and encounter obstacles, making it easier to understand complex wave behaviors.
Can Huygens’ Principle be used to explain phenomena like diffraction and interference?
Yes, Huygens’ Principle can be used to explain phenomena like diffraction and interference. In diffraction, the principle shows how wavefronts bend around obstacles and spread out. In interference, it explains how secondary wavelets from different wavefronts overlap and combine, resulting in constructive and destructive interference patterns.
How does Huygens’ Principle relate to the laws of reflection and refraction?
Huygens’ Principle relates to the laws of reflection and refraction by providing a wave-based explanation for these phenomena. For reflection, the principle shows how secondary wavelets create a new wavefront that obeys the law of reflection (angle of incidence equals angle of reflection). For refraction, it demonstrates how wavelets change speed and direction at an interface, leading to the bending of the wavefront according to Snell’s law.