Electron Emission

Electron emission is a phenomenon that has intrigued scientists for over a century. It’s like a detective story that began in the 1800s, where the first clue was discovered quite by accident.

Thomas Edison, the famous inventor of the light bulb, stumbled upon this mystery in 1880. While working on improving the light bulb, he noticed that an electrical current would flow between a heated filament and a metal plate inside the bulb. This was strange because there was a vacuum inside the bulb, which meant there should be no current flow. Edison didn’t fully understand it, but he found that this “effect” could be used to regulate the current in his light bulbs. He patented this discovery, but the significance of it wasn’t realized until later.

Fast forward to the early 20th century, when scientists were exploring the nature of atoms and electrons. They revisited Edison’s discovery and realized that what he had observed was electrons being “boiled off” the heated filament and attracted to the metal plate. This was named thermionic emission.

The plot thickened when Albert Einstein came into the picture. In 1905, he explained a similar effect called the photoelectric effect, where light, not heat, caused electrons to be emitted from a material. This was groundbreaking because it supported the idea that light could behave as both a wave and a particle, which was a key concept in quantum mechanics.

What is Electron Emission?

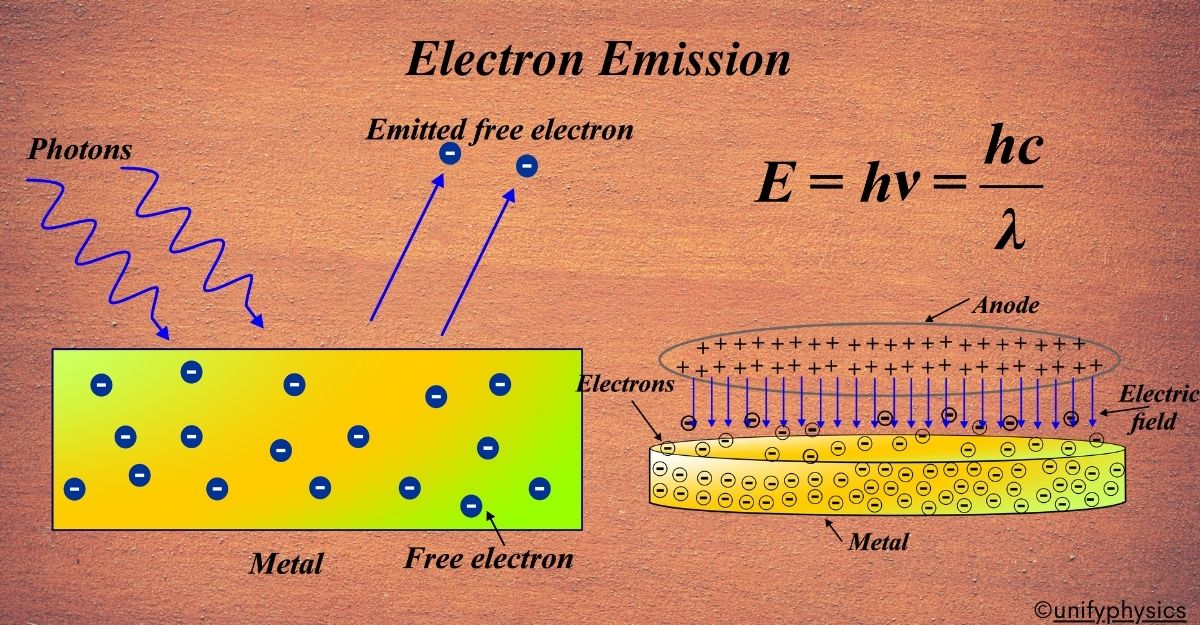
Electron emission is the process by which electrons are ejected from the surface of a material. This can happen due to various factors like heat, light, or electric field. Imagine you’re at a concert, and there’s a barrier between you and the stage. Now, if you have enough energy, you might jump over the barrier to get closer to the music. Similarly, electrons can ‘jump’ out of a material if they have enough energy.

Electron emission is like the electrons at a concert jumping over the barrier. It’s when electrons leave the surface of a material. But instead of music, it’s energy that gets them moving. This can happen in metals, semiconductors, and even in gases.

Now, electrons are usually bound to the atoms of a material, kind of like how you’re held in your seat at the concert by the security guards. But when they gain enough energy, they can break free from the attraction of the atoms, just like you might slip past the guards if you’re quick enough.

This ‘breaking free’ or ‘jumping over the barrier’ is what we call electron emission. It’s a fundamental process that helps us understand how electricity flows through materials and is the basis for many of the electronic devices we use every day.

Work Function:

The work function is the minimum energy required to remove an electron from the surface of a solid. The work function is a key player in the game of electron emission. It’s the threshold that electrons need to cross to go from being part of a material to being free to move and conduct electricity. Think of a soccer ball resting on the ground. To get the ball into the air, you need to kick it with enough force to overcome gravity. Similarly, in the world of atoms, electrons are bound to the nucleus by a force that’s like an atomic version of gravity.

The work function is the minimum ‘kick’ or energy needed to get an electron to leave the surface of a material. It’s like the minimum force you need to apply to the soccer ball to get it off the ground. This energy is specific to each material, just like how kicking a beach ball requires less force than kicking a heavier soccer ball.

In physics terms, the work function is measured in electron volts (eV), which is the energy gained by an electron when it’s accelerated through an electric potential difference of one volt. It’s a tiny amount of energy, but it’s huge on the atomic scale.

So, when we talk about electron emission in terms of the work function, we’re talking about how much energy it takes to free an electron from its atomic bonds. Once the electron has this energy, it can escape into the space outside the material, which is the first step in creating an electric current.

Electron Emission in Intense Electric Field

When a strong electric field is applied, electrons can tunnel out of the material, a process known as field emission. This occurs even at low temperatures where thermal energy is insufficient for electron emission.

Imagine you’re holding onto a pole during a strong wind. The harder the wind blows, the more difficult it becomes to hold on. If the wind is strong enough, it might just pull you away from the pole. In physics, electrons can experience something similar when they’re in a material and an intense electric field is applied.

An intense electric field is like that strong wind, but for electrons. It’s a force that ‘pulls’ on the electrons. Normally, electrons are bound to the atoms in a material, which is like you holding onto the pole. But when the electric field is strong enough, it can ‘pull’ the electrons right out of the material, even if they don’t have enough energy to leave on their own. This is what we call field emission.

This process doesn’t require the material to be hot or light to be shining on it. It’s all about the strength of the electric field. When the field is strong enough, it can create a sort of ‘tunnel’ through the barrier that usually keeps the electrons in place. This tunneling is a quantum mechanical effect, which means it’s one of those weird situations where classical physics rules don’t apply.

Electron Emission from Metals

Metals, with their free electrons, are good emitters. When heated, the thermal energy can overcome the work function, causing thermionic emission. Metals are like a party full of free-moving guests—the electrons. These electrons are not bound tightly to any particular atom, which makes metals good conductors of electricity.

Now, when you heat the metal, it’s like turning up the music at the party. The electrons get more energy and start moving around even more. If you heat the metal enough, some electrons gain so much energy that they can escape from the surface of the metal. This is what we call electron emission from metals.

This process is a bit like water boiling in a pot. When the water gets hot enough, some of it turns into steam and escapes into the air. Similarly, when the metal gets hot enough, some electrons ‘evaporate’ and leave the metal. In physics, we often refer to this as thermionic emission because it’s related to the thermal energy—the heat—that gives the electrons enough energy to leave the metal.

Number of Electrons:

The number of free electrons in a metal has a direct impact on electron emission. Metals have a sea of free electrons that are not bound to any particular atom. These free electrons are what make metals good conductors of electricity. Now, when it comes to electron emission, the more free electrons there are, the higher the probability that some will have enough energy to escape from the metal’s surface.

Think of it like a crowded dance floor. If more people are dancing (free electrons), there’s a higher chance that someone will bump into the door (the metal’s surface) and accidentally open it (escape from the metal). Similarly, if a metal has a high density of free electrons, when you heat the metal or apply an electric field, you’re increasing the chances that more electrons will have the energy to overcome the work function and be emitted.

So, in simple terms, the greater the number of free electrons in a metal, the greater the electron emission, assuming other conditions like temperature and electric field strength are conducive to emission.

Types of Electron Emission

Thermionic Emission

Thermionic emission is all about how heat can give electrons enough energy to break free from their metallic ‘home’ and start an adventure into the surrounding space. Imagine a hot summer day when you’re enjoying a popsicle. As the popsicle heats up in the sun, it starts to melt and drip. Now, replace the popsicle with a piece of metal and the drips with electrons. That’s thermionic emission!

Thermionic emission occurs when a metal is heated to a high temperature. The heat gives energy to the electrons, similar to how the sun’s heat melts the popsicle. As the metal gets hotter, the electrons gain more and more energy. When they have enough energy, they can overcome the attraction of the positive ions in the metal and escape from the surface. It’s like when you’re getting warm and start to sweat; the heat from your body makes the sweat evaporate. In the same way, the heat from the metal makes the electrons ‘evaporate’ into the space around the metal.

Temperature:

As the temperature of a metal increases, thermionic emission increases because more electrons have the energy needed to escape from the metal. As the temperature of a metal increases, the kinetic energy of the electrons also increases. It’s like when you heat water; as it gets hotter, the water molecules move faster until they start to boil and turn into steam. Similarly, as the metal gets hotter, the electrons move faster and faster.

Now, for an electron to escape from the metal, it needs to have enough energy to overcome the work function, which is the energy barrier holding the electrons inside the metal. As the temperature rises, more electrons gain enough energy to overcome this barrier and are emitted from the surface of the metal.

We can describe this relationship mathematically using the Richardson-Dushman equation, which is:

\(\displaystyle J = A T^2 e^{-\frac{\phi}{kT}} \)

• (J) is the current density of emitted electrons.
• (A) is the Richardson constant, which depends on the material.
• (T) is the absolute temperature (in Kelvin).
• (Φ) is the work function of the metal.
• (k) is the Boltzmann constant.
• (e) is the base of the natural logarithm.

The equation shows that the current density of emitted electrons increases exponentially with temperature. This is because the factor \(\displaystyle( e^{-\frac{\phi}{kT}} \)) becomes larger as (T) increases, meaning the probability of electrons overcoming the work function grows significantly with temperature.

Work Function:

Think of the work function as a wall that electrons need to climb over to escape from the metal. The higher the wall (work function), the harder it is for the electrons to get over it. If the wall is lower, it’s easier for them to escape.

In more scientific terms, the work function is the minimum energy needed by an electron to break free from the metal’s surface. During thermionic emission, electrons gain energy from heat. If an electron’s energy from the heat is greater than the work function, it can escape the metal. If the work function is high, you need to heat the metal more to give the electrons enough energy to get out. If the work function is low, less heat is needed for emission to occur.

This type of electron emission is important because it’s the principle behind many devices, like the old vacuum tubes that were used in radios and TVs. These devices work by controlling the flow of these ‘evaporated’ electrons to create signals.

Photoelectric Emission

Imagine you’re outside on a sunny day, and you have a bunch of balloons. Now, these balloons are tied down, and it takes a certain amount of force to pull them free. If a gust of wind (which we’ll compare to light) is strong enough, it can pull the balloons away.

Photoelectric emission is like the wind pulling the balloons away but with light and electrons. When light hits a material, if it has enough energy, it can ‘knock’ electrons off the surface of that material. This happens because light is made up of particles called photons. When a photon with enough energy collides with an electron, it can transfer its energy to the electron. If this energy is more than the work function (the energy needed to pull the electron away), the electron gets ejected. This is the photoelectric effect.

The key thing to remember is that not all light can cause this effect. The light has to be of a high enough energy, which means it has to be of a certain frequency or color. For example, ultraviolet light can cause photoelectric emission in many materials, while red light might not be strong enough.

The equation for the maximum kinetic energy of emitted electrons in the photoelectric effect:

\(\displaystyle KE_{\max} = h\nu – \phi \)

• (KE_max) is the maximum kinetic energy of the emitted electrons.
• (h) is Planck’s constant, a fundamental constant in physics.
• (ν) is the frequency of the incident light.
• (Φ) is the work function of the material, which is the minimum energy needed to remove an electron from the surface.

So, when light shines on a material, each photon carries energy based on its frequency (hν). If a photon has more energy than the work function (Φ), it can give an electron enough energy to escape. The leftover energy becomes the electron’s kinetic energy (KE_max).

In simpler terms, the equation tells us that the energy of light (minus the entry fee) turns into the running speed of the electrons as they leave the material. If the light doesn’t have enough energy (low frequency), the electrons can’t escape, just like if you don’t have enough money for the entry fee, you can’t go to the concert.

Intensity of light:

The intensity of light affects the number of electrons emitted but not their energy. More intense light leads to more electrons being emitted, but only if the photons have enough energy to overcome the work function in the first place. It’s like having more drumbeats in the circle, causing more drummers to stand up and leave.

Think of a drum circle where each drummer is an electron, and the drumbeats are light photons. If you increase the number of drumbeats (light intensity), you’re not making each beat stronger, but you are increasing the number of beats that hit the drums. Similarly, increasing the intensity of light means you’re sending more photons to hit the surface of the material.

Now, if a single drumbeat (photon) is strong enough, it can make a drummer (electron) get up and leave the circle (the material). In photoelectric emission, if a photon has enough energy (which depends on its frequency, not intensity), it can knock an electron out of the material.

When you increase the light intensity, you’re increasing the number of photons hitting the surface, which means more electrons can be knocked out. However, the energy of each photon remains the same, so the intensity doesn’t affect the energy with which the electrons are emitted.

Frequency:

If the frequency of light is too low, it means that each photon of light doesn’t have enough energy to cause photoelectric emission. Imagine you’re playing catch with soft foam balls (low-frequency photons). No matter how many balls you throw at a window (electrons in a material), the balls are just too soft to break the glass and make anything pass through (cause emission).

In the photoelectric effect, each photon must have a certain minimum energy, which is related to its frequency, to knock an electron out of a material. This minimum energy is the work function of the material. If the frequency of the light is below a certain threshold (which means the photons have less energy than the work function), then the electrons won’t get enough energy to escape from the material, no matter how many photons hit the surface (no matter how intense the light is).

If the frequency is too low, nothing happens in terms of electron emission. The electrons simply absorb the energy without being emitted, and the material might get warmer, but no electrons will be knocked loose. It’s like throwing those soft foam balls at the window; you can throw as many as you like, but the window stays intact.

Using low-intensity but high-frequency light in the context of photoelectric emission is like having a few expert marksmen with very precise but not very powerful guns. Even though they don’t shoot many bullets, the ones they do fire are very accurate and can hit the target.

In scientific terms, if the light has a high frequency, each photon has a high energy. Remember, the energy of a photon is given by the equation:

\(\displaystyle E = h \cdot f \)

where (E) is the energy, (h) is Planck’s constant, and (f) is the frequency of the light.

Even if the light is of low intensity (meaning there aren’t many photons), as long as the frequency is above the threshold frequency for the material (which means each photon has enough energy), electrons will be emitted. However, because the intensity is low, the number of electrons emitted will also be low.

With low-intensity but high-frequency light, you’ll get electron emission, but there will be fewer electrons emitted compared to using high-intensity light. It’s the quality (energy) of the light, not the quantity (number of photons), that determines whether electrons can be emitted.

Field Emission

Field emission is all about using a strong electric field to give electrons enough ‘push’ to escape from a material without needing to heat it or shine light on it. Imagine you’re holding a balloon near a wall with spikes. Normally, the balloon doesn’t pop because it’s not touching the spikes. But if you push the balloon towards the spikes with enough force, it will pop. In the world of physics, something similar happens with electrons in field emission.

Field emission occurs when you apply a very strong electric field to a material. This electric field is like the force pushing the balloon towards the spikes. For electrons, the ‘spikes’ are the barrier that usually keeps them inside the material. When the electric field is strong enough, it can ‘push’ the electrons close enough to this barrier that they can escape through a process called quantum tunneling.

Quantum tunneling is a bit like the balloon suddenly popping without touching the spikes because the force is so strong. It’s a weird concept because it doesn’t happen in our everyday lives, but in the quantum world, particles like electrons can sometimes ‘tunnel’ through barriers that would normally be impossible to cross.

Shape Of Material:

The shape of the material has a significant effect on field emission. Imagine you’re trying to pop a balloon with a needle. If you use the pointy end, it pops easily, but if you use the flat end, it’s much harder. Similarly, the shape of a material can make it easier or harder for electrons to be emitted.

In field emission, sharp points or edges on a material’s surface can greatly enhance the electric field locally. This is because the electric field lines are more concentrated at sharp points, just like how the pressure is greater at the pointy end of a needle.

If a material has a sharp, needle-like shape, the electric field around those sharp areas is stronger than around flat areas. This strong field can ‘pull’ electrons out of the material more easily, leading to increased field emission. It’s known as the field enhancement factor, and it’s why materials used for field emission often have a pointed or jagged shape.

The sharper and more pointed the shape of the material, the more effective it is at causing field emission. It’s like having a bunch of tiny needles all ready to pop the balloon of electron binding, allowing the electrons to escape into the wild.

Material’s Composition:

The material’s composition is crucial in determining its effectiveness in field emission. Think of different materials as different types of sponges. Some sponges can absorb a lot of water easily, while others can’t. In the same way, some materials can emit electrons more easily than others.

The composition of a material affects field emission in two main ways:

• Work Function: Different materials have different work functions, which is the energy needed for an electron to escape from the surface. Materials with a lower work function require less energy for their electrons to be emitted. It’s like having a sponge that’s easier to squeeze water out of.
• Electrical Conductivity: Materials that are good conductors of electricity have more free electrons that can be emitted. If a material has a high electrical conductivity, it’s like a sponge that’s full of water and ready to release it.

Additionally, the atomic structure of the material matters too. Materials with a crystalline structure can have different field emission properties compared to those with an amorphous structure. This is because the arrangement of atoms affects how easily electrons can move through the material and reach the surface.

So we can say that the material’s composition affects field emission by influencing the number of available electrons for emission, the energy required to emit them, and the way electrons travel through the material. It’s a bit like choosing the right sponge for the job—some are just better suited for releasing what they hold inside.

Secondary Emission

Secondary emission is the process where incoming electrons cause the emission of additional electrons from a material. Imagine you’re playing a game of pool, and when the cue ball hits another ball, it causes that second ball to move and hit others. In physics, secondary emission is somewhat similar.

Secondary emission occurs when electrons or other primary particles strike a material, and as a result, new electrons are knocked out of that material. It’s like the cue ball causing a chain reaction of other balls moving on the pool table.

An incoming electron (the cue ball) with enough energy hits the atoms in a material (the other pool balls). The energy from this collision can free up more electrons from the material. These newly freed electrons are called secondary electrons because they are emitted as a result of the primary electron’s impact.

It’s important to note that the number of secondary electrons can be greater than the number of primary electrons. This is because one high-energy primary electron can knock out several secondary electrons, just like one good hit in a pool can move several balls.

Energy of Primary Electrons:

The energy of primary electrons has a significant impact on secondary emission. Think of a game of pinball, where the ball (primary electron) hits various targets (atoms in a material). The energy of the ball determines how many other balls (secondary electrons) are released when it hits the targets.

When a primary electron with high energy strikes a material, it can dislodge multiple secondary electrons from the atoms it collides with. This is because the primary electron transfers some of its energy to the electrons in the material, and if this transferred energy is greater than the work function of the material, secondary electrons will be emitted.

• Low-energy primary electrons: They might not have enough energy to free secondary electrons or might free only a few.
• High-energy primary electrons: They can free many secondary electrons because they have enough energy to overcome the binding energy of multiple electrons in the material.

The efficiency of this process is described by the secondary emission coefficient, which is the ratio of the number of secondary electrons emitted to the number of primary electrons striking the material. A higher energy of primary electrons typically leads to a higher secondary emission coefficient.

The higher the energy of the primary electrons, the more secondary electrons can be emitted, much like a more powerful pinball can hit more targets and release more balls.

If primary electrons have very low energy, they won’t be able to cause secondary emission effectively. Think of a game of dodgeball where the goal is to knock players out of the game by hitting them with the ball. If you throw the ball gently (low-energy primary electrons), it’s unlikely to knock anyone out (cause secondary emission). The ball just doesn’t have enough force to make a significant impact.

Similarly, in secondary emission, if the primary electrons don’t have enough energy, they won’t be able to free other electrons from the material’s surface. They might just bounce off or pass through without causing any additional electrons to be emitted. The primary electrons need to have enough kinetic energy to overcome the binding energy that holds the secondary electrons in place.

So, if the primary electrons have very low energy, they will not contribute to secondary emission, and the material will not release additional electrons. It’s like throwing a soft foam ball in dodgeball—it might touch the players, but it won’t knock them out of the game.

The angle of Incidence:

The angle at which primary electrons strike a material, known as the angle of incidence, can affect secondary emission. Imagine you’re skipping stones on a lake. The angle at which you throw the stone affects how it bounces on the water. A flat angle leads to more bounces, while a steep angle might just make the stone sink after one hit.

In secondary emission, when primary electrons hit the surface of a material at a shallow angle (close to parallel to the surface), they tend to travel a longer distance within the material. This increases their chances of interacting with more atoms and, therefore, can potentially knock out more secondary electrons.

On the other hand, if the primary electrons hit the material at a steep angle (close to perpendicular to the surface), they don’t travel as far within the material. This means they have less opportunity to interact with atoms and knock out secondary electrons.

So, the angle of incidence can influence the efficiency of secondary emission. A shallow angle of incidence can lead to a higher yield of secondary electrons, similar to how a stone skips more times when thrown flatly across the water.

Also Read: Polarization Of Light

Applications of Electron Emission

• Television and Computer Monitors: Remember the old bulky TVs and computer monitors? They used Cathode Ray Tubes (CRTs), which worked by electron emission. Electrons were emitted and steered to create images on the screen.
• X-ray Machines: When electrons hit a metal target, they can produce X-rays. This principle is used in X-ray machines, where electron emission helps create the images that let doctors see inside your body.
• Vacuum Tubes: In the past, vacuum tubes were used in radios and early computers. Electron emission was key to their operation, allowing them to amplify signals and switch circuits on and off.
• Electron Microscopes: These powerful microscopes use electron emission to create a beam of electrons that can magnify objects up to 2 million times! This lets scientists see things as small as individual atoms.
• Particle Accelerators: Electron emission is used to generate the initial beam of electrons that are then accelerated to high speeds in particle accelerators, helping physicists study the universe’s fundamental particles.
• Photomultiplier Tubes: These devices detect light and multiply the signal using electron emission. They’re super sensitive and can detect even a single photon of light!
• Semiconductor Manufacturing: Electron beams, created through electron emission, are used to etch incredibly small circuits onto semiconductor chips, the brains of all our electronic devices.
• Solar Cells: In some types of solar cells, light causes electron emission, creating an electric current. This is how sunlight is turned into electricity.
• Lighting: Some types of lamps, like sodium vapor lamps, work by electron emission. Electrons collide with gas atoms inside the lamp, causing them to emit light.

These are just a few examples, but electron emission is a phenomenon that’s at the heart of many technologies we use every day.

Solved Examples

Problem 1: A metal surface with a work function of ( 2.5eV) is illuminated with light of wavelength ( 300nm). Determine if photoelectric emission will occur and, if so, find the maximum kinetic energy of the emitted electrons. (Planck’s constant ( h = 6.63 × 10^-34 Js) and speed of light ( c = 3 × 10⁸ m/s).

Solution: First, calculate the energy of the incident photons using the equation

\(\displaystyle E = \frac{hc}{\lambda} \)

\(\displaystyle E = \frac{6.63 \times 10^{-34} \times 3 \times 10^8}{300 \times 10^{-9}}\)

\(\displaystyle E = \frac{1.989 \times 10^{-25}}{300 \times 10^{-9}} = 6.63 \times 10^{-19} \, \text{J}\)

Convert the energy to electron volts (1 eV = ( 1.6 × 10^-19J):

\(\displaystyle E = \frac{6.63 \times 10^{-19}}{1.6 \times 10^{-19}} = 4.14 \, \text{eV}\)

Since the photon energy (4.14 eV) is greater than the work function (2.5 eV), photoelectric emission will occur. The maximum kinetic energy (\(\displaystyle K_{\text{max}} \)) of the emitted electrons is given by:

\(\displaystyle K_{\text{max}} = E – \text{work function} = 4.14 \, \text{eV} – 2.5 \, \text{eV} = 1.64 \, \text{eV}\)

Photoelectric emission will occur, and the maximum kinetic energy of the emitted electrons is (1.64 eV).

Problem 2: Calculate the thermionic emission current density from a tungsten filament at a temperature of ( 2500 K). The work function of tungsten is ( 4.5 eV), and the Richardson constant ( A = 1.2 × 10⁶ A/m² K²).

Solution: The thermionic emission current density (J) is given by the Richardson-Dushman equation:

\(\displaystyle J = A T^2 \exp \left( -\frac{\phi}{k_B T} \right)\)

Here, (\phi) is the work function, (k_B = 8.617 × 10^-5 eV/K), and (T) is the temperature.

\(\displaystyle J = 1.2 \times 10^6 \times (2500)^2 \exp \left( -\frac{4.5}{8.617 \times 10^{-5} \times 2500} \right)\)

\(\displaystyle J = 1.2 \times 10^6 \times 6.25 \times 10^6 \exp \left( -\frac{4.5}{0.215425} \right)\)

\(\displaystyle J = 7.5 \times 10^{12} \exp \left( -20.88 \right)\)

\(\displaystyle \exp(-20.88) \approx 8.5 \times 10^{-10}\)

\(\displaystyle J = 7.5 \times 10^{12} \times 8.5 \times 10^{-10} \approx 6.375 \times 10^3 \, \text{A/m}^2\)

The thermionic emission current density from the tungsten filament at (2500 K) is approximately (6.375 × 10³ A/m²).

Problem 3: An electron beam with a kinetic energy of ( 100 eV) strikes a metal surface and causes secondary emission. If the secondary emission coefficient (number of secondary electrons emitted per incident electron) is 2, calculate the total number of secondary electrons emitted when 1 mA of primary electron current strikes the surface.

Solution: First, calculate the number of incident electrons per second in the primary beam:

\(\displaystyle I = n e\)

\(\displaystyle n = \frac{I}{e} = \frac{1 \times 10^{-3}}{1.6 \times 10^{-19}} = 6.25 \times 10^{15} \, \text{electrons/s}\)

Given the secondary emission coefficient is 2: Number of secondary electrons emitted per second

\(\displaystyle = 2 \times 6.25 \times 10^{15} = 1.25 \times 10^{16} \, \text{electrons/s}\)

The total number of secondary electrons emitted per second is (1.25 × 10¹⁶).

Problem 4: Calculate the threshold wavelength for photoelectric emission from a metal with a work function of (3.0 eV).

Solution: The threshold wavelength (λ₀) can be found using the equation:

\(\displaystyle\phi = \frac{hc}{\lambda_0}\)

Substitute the given values:

\(\displaystyle 3.0 \, \text{eV} = \frac{6.63 \times 10^{-34} \times 3 \times 10^8}{\lambda_0}\)

Convert the work function to joules (1 eV = ( 1.6 × 10^-19 J):

\(\displaystyle 3.0 \, \text{eV} = 3.0 \times 1.6 \times 10^{-19} \, \text{J} = 4.8 \times 10^{-19} \, \text{J}\)

\(\displaystyle 4.8 \times 10^{-19} = \frac{1.989 \times 10^{-25}}{\lambda_0}\)

\(\displaystyle\lambda_0 = \frac{1.989 \times 10^{-25}}{4.8 \times 10^{-19}} = 414 \times 10^{-9} \, \text{m} = 414 \, \text{nm}\)

The threshold wavelength for photoelectric emission from the metal is (414 nm).

Problem 5: Monochromatic light of wavelength ( 200nm}) is incident on a metal surface, and the stopping potential is measured to be ( 2.0 V). Calculate the work function of the metal.

Solution: First, calculate the energy of the incident photons:

\(\displaystyle E = \frac{hc}{\lambda} = \frac{6.63 \times 10^{-34} \times 3 \times 10^8}{200 \times 10^{-9}} = 9.945 \times 10^{-19} \, \text{J}\)

Convert the energy to electron volts:

\(\displaystyle E = \frac{9.945 \times 10^{-19}}{1.6 \times 10^{-19}} \approx 6.22 \, \text{eV}\)

The kinetic energy of the emitted electrons is given by the stopping potential:

\(\displaystyle K_{\text{max}} = eV_s = 2.0 \, \text{eV}\)

Using the photoelectric equation:

\(\displaystyle E = \phi + K_{\text{max}}\)

\(\displaystyle 6.22 \, \text{eV} = \phi + 2.0 \, \text{eV}\)

\(\displaystyle\phi = 6.22 \, \text{eV} – 2.0 \, \text{eV} = 4.22 \, \text{eV}\)

The work function of the metal is ( 4.22 eV).

FAQs