Davisson Germer Experiment

In the early 20th century, the nature of light was a hot topic. Scientists knew it behaved like a wave, thanks to Maxwell’s equations. However, in 1905, Albert Einstein proposed that light could also be seen as particles, or “quanta” of energy, which he called photons. This idea was revolutionary and earned him a Nobel Prize in Physics in 1921.

In 1924, a French physicist named Louis de Broglie introduced a bold new idea: if light can be both a wave and a particle, maybe all matter has this dual nature. He suggested that particles of matter, like electrons, could also behave like waves. This was a radical shift from the existing view that matter was purely particle-like.

Clinton Davisson and Lester Germer, working at Western Electric (later Bell Labs), were not initially trying to prove de Broglie’s theory. They were studying the surface of nickel using electron beams. But in 1927, they stumbled upon something unexpected: when they fired electrons at a nickel crystal, the electrons scattered in a pattern that resembled the diffraction patterns of waves, not just particles.

Davisson and Germer’s accidental discovery was monumental. It confirmed de Broglie’s hypothesis and showed that electrons could indeed exhibit wave-like properties. This experiment was one of the first to demonstrate the wave-particle duality of matter, laying the groundwork for the field of quantum mechanics.

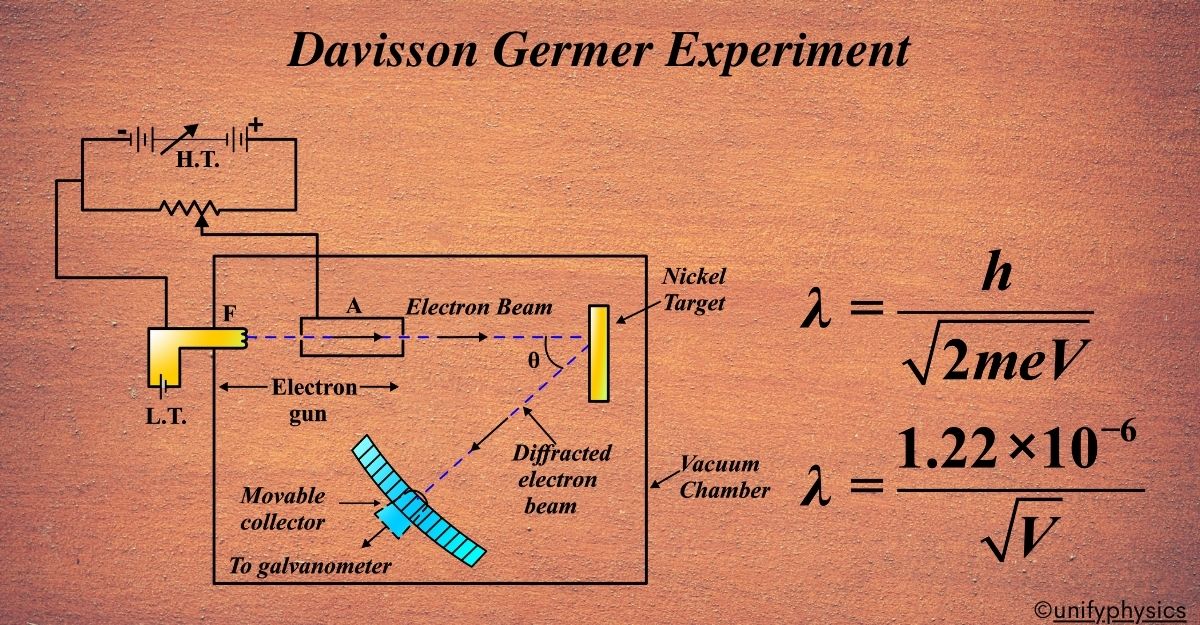
Davisson Germer Experiment Setup

The setup for the Davisson and Germer experiment was ingeniously simple yet effective. It consisted of several key components:

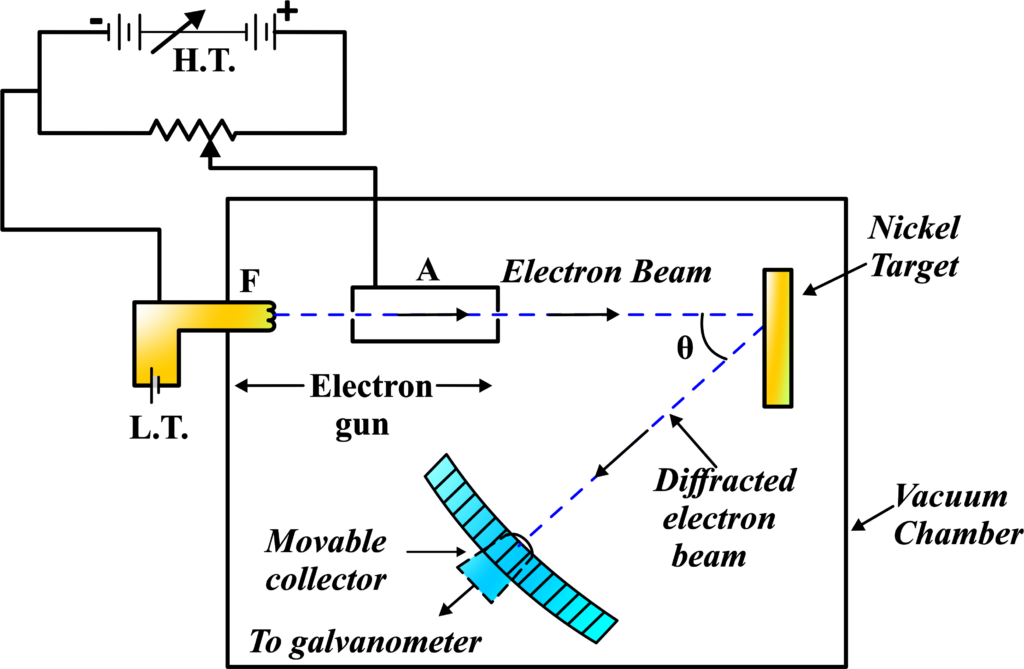
• Electron Gun: This is a device that produces a beam of electrons. In the experiment, it was made from a tungsten filament coated with barium oxide. When heated, it emits electrons through a process called thermionic emission.
• Electrostatic Particle Accelerator: Once the electrons were emitted, they were accelerated using two oppositely charged plates—one positive and one negative. This acceleration was crucial because it gave the electrons enough energy to produce a clear diffraction pattern upon hitting the target.
• Collimator: This is essentially a tube with a narrow opening that ensures the electron beam is well-directed and straight when it hits the target. Think of it as the “aiming” part of the setup.
• Nickel Crystal Target: The target for the electron beam was a crystal of nickel. The crystal was mounted so that it could be rotated to various angles during the experiment.
• Detector: After the electrons hit the nickel crystal, they scattered in different directions. A detector was used to measure the intensity of these scattered electrons. It could move in a semicircular arc around the crystal to detect electrons at different angles.
• Vacuum Chamber: All of these components were placed inside a vacuum chamber to prevent the electrons from scattering off air molecules, which would interfere with the experiment.

The Thought Behind the Setup: The idea was to see if electrons, when directed at a crystal, would display a pattern similar to that of waves being diffracted. By carefully measuring the angles at which the electrons were scattered and the intensity of the scattered electrons, Davisson and Germer hoped to reveal the wave-like nature of electrons.

This setup was a physical manifestation of the theoretical predictions of de Broglie, who suggested that particles could behave like waves. The Davisson and Germer experiment was designed to put this bold hypothesis to the test.

Choice Of Material For Experiment

The choice of material has a significant impact on the diffraction patterns observed in experiments like the one conducted by Davisson and Germer. Here’s how different materials can affect the patterns:

Crystal Structure: Each material has a unique crystal structure, which determines the arrangement of atoms within the crystal. This structure affects the diffraction pattern because the pattern is essentially a map of the crystal’s atomic arrangement. Different structures will produce different patterns.

Lattice Spacing: The spacing between the atoms in a crystal, known as lattice spacing, varies from material to material. Since diffraction patterns are influenced by the distance between these atomic planes, materials with different lattice spacings will produce diffraction patterns with different spacings between the fringes.

Atomic Number: The atomic number of the elements in the material affects the strength of the interaction between the incoming electrons and the atoms in the crystal. Higher atomic numbers generally result in stronger interactions, which can lead to more intense diffraction peaks.

Electron Density: Materials with higher electron densities can scatter electrons more effectively, leading to clearer and more pronounced diffraction patterns. Conversely, materials with lower electron densities might produce weaker patterns.

Surface Quality: The quality of the crystal surface, including its cleanliness and the presence of defects, can also influence the diffraction pattern. A cleaner, more perfect crystal will produce a clearer and more regular pattern.

Temperature: Temperature can affect the diffraction pattern as it can cause expansion or contraction of the crystal lattice, thus altering the lattice spacing and potentially the diffraction pattern.

The choice of material for the target in an electron diffraction experiment is crucial because it determines the nature of the diffraction pattern that will be observed. The crystal structure, lattice spacing, atomic number, electron density, surface quality, and temperature all play roles in shaping the pattern.

Nickel Crystal:

The choice of a nickel crystal as the target in the Davisson and Germer experiment was partly serendipitous. Initially, they were studying the surface of nickel because of its regular crystal structure, which was useful for scattering experiments. However, during their experiments, an accident occurred where air entered their vacuum chamber and oxidized the nickel surface. To remove the oxide layer, they heated the nickel, which inadvertently transformed the polycrystalline nickel into a single large crystal.

When they resumed their experiments with this large nickel crystal, they observed unexpected peaks in their data, which indicated that the electrons were being diffracted. This was a key observation because diffraction is a property of waves, and it supported the hypothesis that electrons have wave-like properties. The use of nickel, therefore, turned out to be a fortunate choice that led to the confirmation of de Broglie’s theory of matter waves.

This accidental discovery was crucial because it provided the first concrete evidence of the wave nature of electrons, which was a significant step forward in the development of quantum mechanics. The experiment showed that matter could exhibit wave-like behavior, which was a groundbreaking concept at the time.

Other Materials:

In the Davisson and Germer experiment, while nickel was used due to its crystalline structure and the serendipitous creation of a large single crystal, other materials could also have been used as targets for electron diffraction. The key requirement is that the material should have a well-defined and regular crystal structure to produce clear diffraction patterns. Here are some alternatives:

• Other Single Crystals: Materials like silicon and germanium could be used, as they also have regular crystal structures and are commonly used in diffraction experiments today.
• Magnetically Textured Powders: These can serve as an alternative to single crystals. They are non-magnetic materials that can be oriented magnetically to diffract electrons similarly to a large single crystal.
• Microcrystals: With advancements in electron diffraction techniques, even tiny microcrystals can now be used to determine the structures of small molecules. This method, known as microcrystal electron diffraction (MicroED), can rapidly image the structures of small molecules, including those found in mixtures.
• Amorphous Materials: While they lack long-range order and do not produce Bragg spots, amorphous materials can still diffract electrons, displaying broad rings in diffraction patterns that confirm short-range order.

These materials could potentially have been used by Davisson and Germer or by researchers following in their footsteps, to further explore the wave nature of electrons and other particles.

Working of Davisson Germer Experiment

The experiment aimed to observe how electrons behave when they encounter a crystal. The hypothesis was that if electrons have wave-like properties, they would show diffraction patterns similar to those observed with light waves.

Electron Emission Imagine a tiny electron gun, much like a miniature cannon, that fires electrons instead of cannonballs. This gun consists of a heated filament, often made of tungsten. When this filament is heated, it emits electrons through a process known as thermionic emission. It’s akin to boiling water; when heated enough, the water turns into steam. Similarly, when the filament gets hot, it releases electrons, which are then ready for their quantum journey.

Acceleration Once the electrons are emitted, they need to be sped up to have enough energy to showcase their wave-like properties. This is done using an electrostatic particle accelerator, which consists of two plates charged with high voltage. The electrons, being negatively charged, are attracted to the positive plate and repelled by the negative one, causing them to accelerate rapidly. It’s like giving the electrons a powerful slingshot that propels them toward their target at high speed.

Collimation: Now that our electrons are moving fast, we need to ensure they travel in a straight, narrow beam toward the target. This is where a collimator comes in. It’s a device with a fine opening that narrows down the electron beam, much like how a nozzle focuses a stream of water. This focused beam is crucial for the precision required in the experiment.

Interaction with the Target: The target in this experiment is a nickel crystal. When the finely focused beam of electrons hits this crystal, they interact with the atoms within the crystal’s lattice. This interaction is similar to throwing a ball into a forest; the ball bounces off the trees in various directions. In our quantum forest, the ‘trees’ are the atoms of the nickel crystal, and the ‘balls’ are the electrons.

Diffraction: As the electrons pass through the spaces between the atoms of the nickel crystal, they begin to behave not just as particles but as waves. They spread out and overlap, creating patterns of interference. This phenomenon, known as diffraction, is the same thing that happens when you drop two pebbles into a pond and the ripples intersect, creating patterns on the water’s surface.

Detection: Finally, to observe this quantum spectacle, a detector is used. It moves around the nickel crystal, capturing the electrons after they’ve been scattered. The detector is connected to a device that measures the intensity of the scattered electrons at different angles. It’s like having a camera that takes pictures of the ripples in our pond from different positions, allowing us to see the full pattern.

If electrons were purely particle-like, they would bounce off the atoms in predictable directions. However, if they had wave-like properties, they would create an interference pattern—a series of bright and dark spots—depending on how the waves combined after scattering.

When the experiment was conducted, the electrons indeed produced a pattern of scattered intensities that varied with the angle, just like waves interfering after passing through a slit or around an obstacle. This was the “aha” moment that showed electrons could behave like waves.

Wave-Particle Duality: The Davisson and Germer experiment is fundamentally related to the concept of wave-particle duality in quantum mechanics. Wave-particle duality is the idea that every particle or quantum entity can be described as either a particle or a wave. It expresses the inability of classical concepts like “particle” or “wave” to fully describe the behavior of quantum-scale objects.

The Davisson and Germer experiment provided the first clear evidence of this duality. By firing electrons at a nickel crystal and observing the resulting diffraction pattern, they demonstrated that electrons—traditionally thought of as particles—could exhibit wave-like behavior. This was a direct observation of wave-particle duality.

The experiment confirmed Louis de Broglie’s hypothesis, which proposed that particles such as electrons have a wave associated with them. The observed diffraction patterns could only be explained if the electrons were behaving like waves, spreading out and interfering with each other.

This discovery was a pivotal moment in physics. It showed that the classical distinction between waves and particles was no longer valid at the quantum level. The results of the Davisson and Germer experiment, along with the Compton effect discovered by Arthur Compton, established the wave-particle duality hypothesis as a fundamental principle of quantum theory.

The Davisson and Germer experiment bridged the gap between classical physics and quantum mechanics, providing experimental proof that matter has both wave and particle characteristics, depending on how it’s observed. This duality is now a key concept in understanding the behavior of particles at the quantum scale.

Davisson and Germer Experiment Observations

When Davisson and Germer conducted their experiment, they made several critical observations that were instrumental in understanding the wave nature of electrons:

• Intensity Peaks: They noticed that as they varied the angle at which the electron beam struck the nickel crystal, the intensity of the scattered electrons showed distinct peaks at certain angles.
• Voltage Variation: By changing the accelerating voltage applied to the electrons, they could adjust the energy of the electrons. They observed that the position of the intensity peaks changed with the voltage, suggesting a relationship between the electron’s energy and the diffraction pattern.
• Constructive Interference: The most significant observation was at an accelerating voltage of 54 volts and a scattering angle of 50 degrees. Here, they found a strong peak in intensity, indicating constructive interference of the electrons—just like waves combining to create a brighter light.
• Confirmation of Wave Behavior: These observations confirmed that electrons were not just being deflected as particles would be; they were interfering with each other like waves. This was a direct observation of the wave-like behavior of matter.

These observations were groundbreaking because they provided empirical evidence that electrons could exhibit wave-like properties. The peaks in intensity were analogous to the bright fringes seen in light diffraction experiments, which are a hallmark of wave interference patterns. The Davisson and Germer experiment’s observations were a pivotal moment in physics, as they offered the first concrete proof that particles at the quantum level do not behave strictly as particles but also as waves.

Co-relating Davisson Germer Experiment and de Broglie Relation

Firstly, Louis de Broglie proposed that particles can have wave-like properties. He introduced a fundamental equation to describe the wavelength (λ) associated with a particle:

\(\displaystyle \lambda = \frac{h}{p} \)

where (h) is Planck’s constant and (p) is the momentum of the particle.

The Experiment’s Connection to de Broglie’s Relation: In the Davisson and Germer experiment, electrons were accelerated and then scattered off a nickel crystal. They observed a diffraction pattern, which indicated that electrons were behaving like waves.

To correlate their observations with de Broglie’s relation, they used the equation to calculate the expected wavelength of the electrons based on their momentum. The momentum (p) of an electron can be related to its kinetic energy (KE), which is given by the accelerating voltage (V) in the experiment:

\(\displaystyle KE = \frac{1}{2}mv^2 \)

Since the electron is accelerated through a potential difference (V), the kinetic energy can also be written as:

\(\displaystyle KE = eV \)

(e) is the charge of the electron (approximately ( 1.602 × 10^-19 C). The momentum (p) of the electron is related to its kinetic energy by the equation:

\(\displaystyle p = \sqrt{2mKE} \)

Substituting (KE) with (eV), we get:

\(\displaystyle p = \sqrt{2meV} \)

Now, we substitute the expression for (p) into de Broglie’s equation:

\(\displaystyle \lambda = \frac{h}{\sqrt{2meV}} \)

To make this equation easier to use, we can introduce a constant to simplify the expression. This constant is derived from the values of (h), (e), and (m) (the mass of the electron, approximately ( 9.109 × 10^-31 kg), and it is often rounded to \(\displaystyle 1.227 \times 10^{-6} m\sqrt{\text{V}}\) for convenience. So the simplified de Broglie’s equation becomes:

\(\displaystyle \lambda = \frac{1.227 \times 10^{-6}}{\sqrt{V}} \text{ m} \)

Example: In the Davisson and Germer experiment, when they used an accelerating voltage of 54 volts, the de Broglie wavelength of the electrons can be calculated as:

\(\displaystyle\lambda = \frac{1.227 \times 10^{-6}}{\sqrt{54}} \text{ m} \)

This calculation yields a wavelength of approximately ( 0.167 × 10^-9) m, or 0.167 nm, which matched the wavelength observed in the experiment for the diffraction pattern.

This derivation shows how the Davisson and Germer experiment confirmed de Broglie’s hypothesis by demonstrating that electrons exhibit wave-like properties with a wavelength that can be predicted by their momentum. It’s a beautiful example of theoretical prediction being confirmed by experimental evidence. This correlation was crucial because it provided experimental confirmation of de Broglie’s theoretical prediction. It showed that electrons, which were known to be particles, also exhibited wave-like behavior, characterized by a specific wavelength.

What happens if the accelerating voltage is increased?

When Davisson and Germer set the accelerating voltage to 54 volts, they found that the wavelength of the electrons was about 0.167 nm, which matched the wavelength calculated using de Broglie’s relation.

When the accelerating voltage in an electron diffraction experiment like the Davisson and Germer experiment is increased, the kinetic energy of the electrons also increases. According to de Broglie’s relation, the wavelength (λ) of a particle is inversely proportional to its momentum (p), which is related to the kinetic energy (KE). The relationship can be expressed as:

\(\displaystyle \lambda = \frac{h}{\sqrt{2mKE}} \)

As the kinetic energy (KE) is directly proportional to the accelerating voltage (V), given by (KE = eV )

\(\displaystyle \lambda = \frac{h}{\sqrt{2meV}} \)

Therefore, with a higher accelerating voltage, the electrons have a shorter wavelength. This shorter wavelength means that the electrons are diffracted less, and as a result, the diameters of the diffraction rings observed on a detection screen decrease. This is a key aspect of electron diffraction experiments and is crucial for understanding the wave-particle duality of electrons.

Also Read: Electron Emission

Outcomes of the Davisson Germer Experiment

The Davisson and Germer experiment led to several significant outcomes that reshaped our understanding of quantum physics:

• Confirmation of Wave Nature: The experiment provided the first direct evidence that electrons exhibit wave-like properties. The diffraction pattern observed was similar to that produced by waves, not particles.
• Support for de Broglie’s Hypothesis: The results supported Louis de Broglie’s hypothesis that matter has a dual nature, behaving both as particles and waves. The wavelengths calculated from the experiment matched the predictions made by de Broglie’s equation.
• Quantum Mechanics Milestone: This experiment was a pivotal moment in the development of quantum mechanics. It showed that the classical physics view of matter as just particles was incomplete.
• Technological Advancements: The confirmation of electron wave properties paved the way for technologies like electron microscopy, which relies on the wave nature of electrons to view objects at the nanoscale.
• Educational Impact: The experiment has become a fundamental part of physics education, illustrating the principles of wave-particle duality and quantum mechanics to students around the world.

Solved Examples

Problem 1: In the Davisson-Germer experiment, electrons are accelerated through a potential difference of 54V. Calculate the de Broglie wavelength of these electrons. (Given: mass of electron ( \(\displaystyle m = 9.11 \times 10^{-31} \, \text{kg} \)), charge of electron (\(\displaystyle  e = 1.6 \times 10^{-19} \, \text{C} \)), Planck’s constant (\(\displaystyle h = 6.63 \times 10^{-34} \, \text{Js} \)).

Solution: The kinetic energy (KE) of the electron is given by:

KE = eV

Substituting the given values:

\(\displaystyle KE = 1.6 \times 10^{-19} \times 54 = 8.64 \times 10^{-18} \, \text{J}\)

The kinetic energy is also given by:

\(\displaystyle KE = \frac{1}{2} mv^2\)

Solving for (v):

\(\displaystyle v = \sqrt{\frac{2 \times KE}{m}} = \sqrt{\frac{2 \times 8.64 \times 10^{-18}}{9.11 \times 10^{-31}}}\)

\(\displaystyle v = \sqrt{1.896 \times 10^{13}} = 4.35 \times 10^6 \, \text{m/s}\)

The de Broglie wavelength (\lambda) is:

\(\displaystyle \lambda = \frac{h}{mv}\)

\(\displaystyle \lambda = \frac{6.63 \times 10^{-34}}{9.11 \times 10^{-31} \times 4.35 \times 10^6}\)

\(\displaystyle \lambda = \frac{6.63 \times 10^{-34}}{3.96 \times 10^{-24}} = 1.675 \times 10^{-10} \, \text{m}\)

The de Broglie wavelength of the electrons is (\(\displaystyle 1.675 \times 10^{-10} \, \text{m}\)).

Problem 2: In the Davisson-Germer experiment, the maximum intensity of the scattered electrons is observed at an angle of 50°. Calculate the interplanar spacing \(d\) of the crystal used, given the de Broglie wavelength of the electrons is \(1.65 \times 10^{-10} \, \text{m}\).

Solution: Using Bragg’s law for maximum intensity:

\(\displaystyle n\lambda = 2d\sin\theta\)

For the first-order diffraction (n=1):

\(\displaystyle\lambda = 2d\sin\theta\)

Solving for (d ):

\(\displaystyle d = \frac{\lambda}{2\sin\theta}\)

Substituting the given values:

\(\displaystyle d = \frac{1.65 \times 10^{-10}}{2 \sin 50^\circ}\)

\(\displaystyle d = \frac{1.65 \times 10^{-10}}{2 \times 0.766} = \frac{1.65 \times 10^{-10}}{1.532} \)

\(\displaystyle = 1.08 \times 10^{-10} \, \text{m}\)

The interplanar spacing (d) of the crystal is (\(\displaystyle 1.08 \times 10^{-10} \, \text{m}\)).

Problem 3: In the Davisson-Germer experiment, electrons are accelerated through a potential difference of 50V. If the observed de Broglie wavelength is (\(\displaystyle 1.7 \times 10^{-10} \, \text{m}\)), calculate the work function of the material used in the experiment.

Solution: First, calculate the kinetic energy of the electrons:

\(\displaystyle KE = eV = 1.6 \times 10^{-19} \times 50 = 8 \times 10^{-18} \, \text{J}\)

The de Broglie wavelength (λ) is given by:

\(\displaystyle\lambda = \frac{h}{\sqrt{2mKE}}\)

Rearranging to solve for (KE):

\(\displaystyle KE = \frac{h^2}{2m\lambda^2}\)

Substitute the given values:

\(\displaystyle KE = \frac{(6.63 \times 10^{-34})^2}{2 \times 9.11 \times 10^{-31} \times (1.7 \times 10^{-10})^2}\)

\(\displaystyle KE = \frac{4.39 \times 10^{-67}}{2 \times 9.11 \times 10^{-31} \times 2.89 \times 10^{-20}} = \frac{4.39 \times 10^{-67}}{5.26 \times 10^{-50}} \)

\(\displaystyle = 8.34 \times 10^{-18} \, \text{J}\)

The work function (φ) is given by:

\(\displaystyle\phi = eV – KE\)

\(\displaystyle\phi = 8 \times 10^{-18} – 8.34 \times 10^{-18} = -0.34 \times 10^{-18} \, \text{J}\)

Since the work function cannot be negative, there may be an error in calculation or assumptions. Typically, this requires revisiting experimental setup or values. Due to the negative result, check the experimental setup and values; reevaluation is needed.

Problem 4: If the de Broglie wavelength of electrons in a Davisson-Germer experiment is (\(\displaystyle 1.66 \times 10^{-10} \, \text{m}\)), calculate the accelerating voltage used. (Given: mass of electron (\(\displaystyle m = 9.11 \times 10^{-31} \, \text{kg} \)), charge of electron (\(\displaystyle e = 1.6 \times 10^{-19} \, \text{C} \)), Planck’s constant (\(\displaystyle h = 6.63 \times 10^{-34} \, \text{Js} \)).

Solution: Using the de Broglie wavelength formula:

\(\displaystyle\lambda = \frac{h}{\sqrt{2meV}}\)

Rearranging to solve for (V):

\(\displaystyle V = \frac{h^2}{2me\lambda^2}\)

Substituting the given values:

\(\displaystyle V = \frac{(6.63 \times 10^{-34})^2}{2 \times 9.11 \times 10^{-31} \times 1.6 \times 10^{-19} \times (1.66 \times 10^{-10})^2}\)

\(\displaystyle V = \frac{4.39 \times 10^{-67}}{2 \times 9.11 \times 10^{-31} \times 1.6 \times 10^{-19} \times 2.76 \times 10^{-20}}\)

\(\displaystyle V = \frac{4.39 \times 10^{-67}}{8.07 \times 10^{-50}} = 54.42 \, \text{V}\)

The accelerating voltage used is (54.42 V).

Problem 5: In the Davisson-Germer experiment, electrons are accelerated through a potential difference of 54V, and the observed de Broglie wavelength is (\(\displaystyle 1.67 \times 10^{-10} \, \text{m}\)). Calculate the angle of incidence at which maximum intensity is observed, given the interplanar spacing (\(\displaystyle d = 1.08 \times 10^{-10} \, \text{m} \)).

Solution: Using Bragg’s law:

\(\displaystyle n\lambda = 2d\sin\theta\)

For the first-order diffraction (n=1):

\(\displaystyle\lambda = 2d\sin\theta\)

Solving for (\theta):

\(\displaystyle\sin\theta = \frac{\lambda}{2d}\)

Substituting the given values:

\(\displaystyle\sin\theta = \frac{1.67 \times 10^{-10}}{2 \times 1.08 \times 10^{-10}} = \frac{1.67}{2.16} = 0.772\)

\(\displaystyle\theta = \sin^{-1}(0.772) = 50.5^\circ\)

The angle of incidence at which maximum intensity is observed is (50.5^∘).

Problem 6: An electron beam in the Davisson-Germer experiment produces a maximum intensity at an angle of 45° with an interplanar spacing of (\(\displaystyle 1.10 \times 10^{-10} \, \text{m}\)). Verify the de Broglie wavelength if the electrons are accelerated by 54V.

Solution: Using Bragg’s law:

\(\displaystyle n\lambda = 2d\sin\theta\)

For the first-order diffraction (n=1):

\(\displaystyle\lambda = 2d\sin\theta\)

Substituting the given values:

\(\displaystyle\lambda = 2 \times 1.10 \times 10^{-10} \times \sin 45^\circ\)

\(\displaystyle\lambda = 2 \times 1.10 \times 10^{-10} \times 0.707 = 1.556 \times 10^{-10} \, \text{m}\)

Calculate the theoretical de Broglie wavelength using the given accelerating voltage:

\(\displaystyle\lambda = \frac{h}{\sqrt{2meV}}\)

\(\displaystyle\lambda = \frac{6.63 \times 10^{-34}}{\sqrt{2 \times 9.11 \times 10^{-31} \times 1.6 \times 10^{-19} \times 54}}\)

\(\displaystyle\lambda = \frac{6.63 \times 10^{-34}}{\sqrt{1.57 \times 10^{-17}}} = \frac{6.63 \times 10^{-34}}{3.97 \times 10^{-9}} \)

\(\displaystyle = 1.67 \times 10^{-10} \, \text{m}\)

The calculated de Broglie wavelength from Bragg’s law is (\(\displaystyle 1.556 \times 10^{-10} \, \text{m}\)) and the theoretical wavelength from the accelerating voltage is ( \(\displaystyle 1.67 \times 10^{-10} \, \text{m}\)). The slight discrepancy is due to approximations and experimental uncertainties.

FAQs