Bohr Model of Hydrogen Atom

Before Bohr, there was a quest to understand the atom’s structure. In 1897, J.J. Thomson discovered the electron and proposed the ‘plum pudding model,’ which suggested that electrons were scattered within a ‘pudding’ of positive charge. However, this model couldn’t explain certain experimental results like the emission spectra or the outcomes of alpha particle scattering experiments.

Ernest Rutherford’s gold foil experiment in 1909 led to the discovery that atoms have a small, dense, positively charged nucleus with electrons orbiting around it. This was a significant step forward but still had its flaws. According to classical physics, electrons in motion should emit energy and spiral into the nucleus, leading to the collapse of the atom – which obviously doesn’t happen in reality.

Niels Bohr, building on Rutherford’s model and Planck’s quantum theory, introduced his model in 1913. He proposed that electrons orbit the nucleus in fixed orbits or shells and that these electrons could only occupy certain energy levels. This was a bold step as it defied classical physics, suggesting that the laws of motion did not apply to electrons in atoms in the same way they do to larger objects.

Bohr introduced the idea that electrons could ‘jump’ between these fixed orbits by absorbing or emitting energy in discrete packets called quanta. This explained why atoms emitted light in specific wavelengths, leading to the characteristic line spectra.

For his groundbreaking work on the structure of atoms and his contributions to quantum mechanics, Niels Bohr was awarded the Nobel Prize in Physics in 1922.

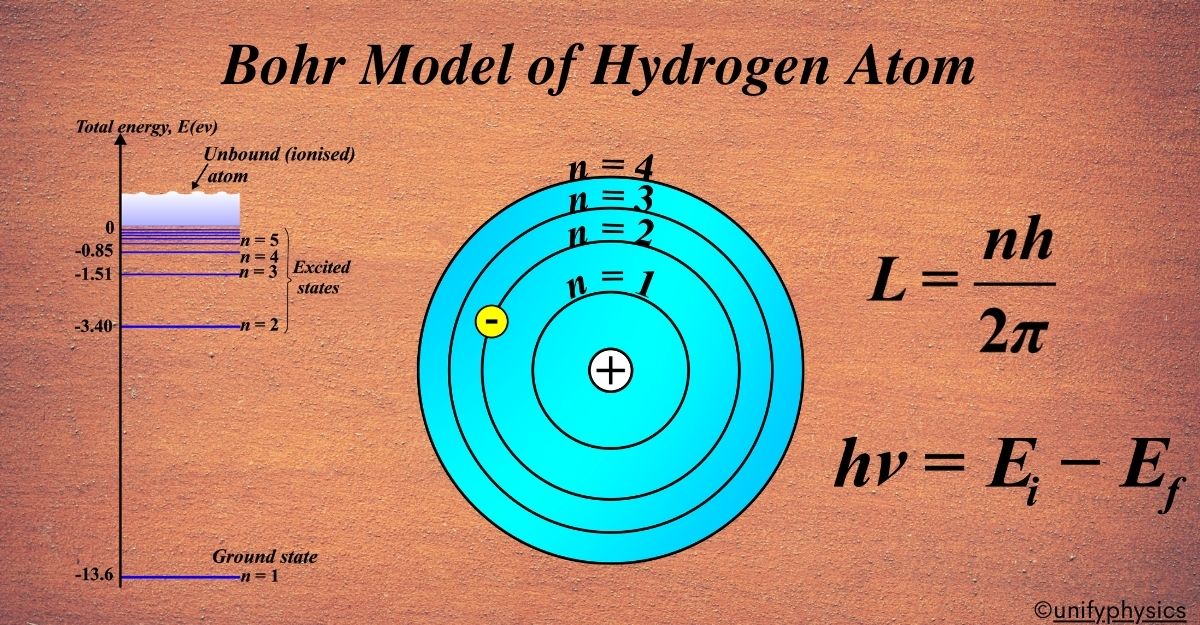
Bohr Model of Hydrogen Atom

The Bohr Model, often referred to as the Planetary Model of the Atom, is a concept that simplifies the complex nature of atomic structures. It’s particularly focused on the hydrogen atom, which is the simplest atom with only one electron. Here’s an easy-to-understand explanation:

Imagine the atom as a miniature solar system. In the center, you have the nucleus, which is like the sun, and orbiting around it are electrons, similar to planets circling the sun. This is why it’s called the Planetary Model.

Before this, scientists thought electrons could be anywhere around the nucleus, but Bohr suggested that there are special spots—like designated seats in a theater—where electrons are allowed to sit.

In the Bohr Model, the electron orbits are not random paths but specific, well-defined circles. Each orbit represents a stable ‘home’ for the electron where it can stay without losing energy. Just like planets have certain distances from the sun where they can orbit stably, electrons have certain orbits at fixed distances from the nucleus where they can exist.

This model was a significant step forward because it introduced a new way of thinking about where electrons can be. Before this, scientists thought electrons could be anywhere around the nucleus, but Bohr suggested that there are special spots—like designated seats in a theater—where electrons are allowed to sit.

So, when we talk about the Bohr Model, we’re picturing electrons in their specific orbits, peacefully orbiting the nucleus just like planets orbit the sun, in a neat, orderly fashion. This idea helped scientists understand more about how atoms work and why they emit light in specific colors under certain conditions.

Limitations of Ernest Rutherford’s model: Niels Bohr addressed the limitations of Ernest Rutherford’s model by introducing several key improvements:

Quantum Orbits: Bohr proposed that electrons move in fixed orbits around the nucleus and that these orbits have quantized energy levels. This means that electrons can only exist in certain energy states, and this quantization prevents them from spiraling into the nucleus, which was a major issue in Rutherford’s model.

Energy Emission and Absorption: He introduced the concept that electrons could jump between these fixed energy levels. When an electron moves to a higher energy orbit, it absorbs a quantum of energy. Conversely, when it falls to a lower energy orbit, it emits energy. This explained the discrete spectral lines observed in atomic spectra.

Angular Momentum Quantization: Bohr also postulated that the angular momentum of electrons in their orbits is quantized. This means that the angular momentum is an integral multiple of the reduced Planck’s constant (\(\displaystyle\hbar = \frac{h}{2\pi} \)), which further supported the stability of the atom.

Predictive Power: Bohr’s model had strong predictive power, especially for the hydrogen atom. It could predict the frequencies of the spectral lines emitted by hydrogen, which was something Rutherford’s model could not do.

Stability of Atoms: By requiring that electrons move in orbits of fixed size and energy, Bohr’s model provided a solution to the stability problem of the atom. In Rutherford’s model, the electrons were expected to release energy continuously and eventually collapse into the nucleus. Bohr’s model explains why this does not happen.

These improvements made Bohr’s model a significant advancement over Rutherford’s model, leading to a better understanding of atomic structure and laying the groundwork for modern quantum mechanics.

Bohr’s Equation

Bohr’s Equation is a way to calculate the energy of an electron at different levels in a hydrogen atom. It’s like knowing how much money you have in your wallet depending on which pocket you put it in.

Here’s the equation:

\(\displaystyle E(n) = -\frac{1}{n^2} \times 13.6\,eV \)

In this equation:

• E(n) is the energy of the electron when it’s in the nth orbit.
• (n) is the principal quantum number, which can be any positive integer (1, 2, 3, …).
• (13.6 eV) is the energy of the electron in its lowest energy level, or the ground state.

The negative sign means that the energy is lower than a free electron that’s not attached to an atom. Think of it as being in debt; the electron owes energy to get free from the atom.

As (n) gets bigger, the fraction (\(\displaystyle \frac{1}{n^2} \)) gets smaller, which means the electron has less negative energy (less debt), and it’s easier for the electron to leave the atom (like paying off a small loan).

Bohr’s Equation tells us how ‘energetic’ an electron is depending on which ‘step’ (orbit) it’s on in the atom’s ‘ladder’ (energy levels). To derive this, we’ll use a few concepts from physics:

• Centripetal Force: This is the force that keeps the electron in a circular orbit. It’s like the string that holds a spinning ball in a circle.
• Electrostatic Force: This is the attractive force between the positively charged nucleus and the negatively charged electron.
• Quantization of Angular Momentum: Bohr said that the angular momentum of an electron in orbit is a whole number multiple of ( \(\displaystyle\frac{h}{2\pi} \)).

The centripetal force required to keep the electron in orbit is provided by the electrostatic force. So, we set the centripetal force equal to the electrostatic force:

\(\displaystyle \frac{m_e v^2}{r} = \frac{k e^2}{r^2} \)

Here, (m_e) is the mass of the electron, (v) is its velocity, (r) is the radius of the orbit, (k) is Coulomb’s constant, and (e) is the charge of the electron.

Now, we use the quantization of angular momentum:

\(\displaystyle m_e v r = n \frac{h}{2\pi} \)

By combining these two equations, we can solve for (v) and (r) in terms of (n), the principal quantum number. Finally, we find the energy of the electron by adding its kinetic energy and potential energy:

\(\displaystyle E = \frac{1}{2} m_e v^2 – \frac{k e^2}{r} \)

After substituting (v) and (r) from our previous steps and simplifying, we get Bohr’s Equation for the energy levels of the electron:

\(\displaystyle E(n) = -\frac{1}{n^2} \times 13.6\,eV \)

This equation tells us the energy of an electron based on which orbit it’s in. The negative sign indicates that the electron is bound to the nucleus; the closer it is to the nucleus (the smaller the value of (n), the more tightly it’s bound, and the more energy it would take to free it.

Bohr Radius

Bohr’s radius is a term that comes up when we talk about the Bohr Model of the hydrogen atom. It’s a specific value that represents the average distance from the nucleus to the electron in the lowest energy state, or ground state, of the hydrogen atom.

To make it simple, think of Bohr’s radius as the “home base” distance where the electron likes to hang out when it’s not excited by any external energy. It’s like the default circle around the nucleus where the electron can be found most of the time.

In numbers, Bohr’s radius is approximately (\(\displaystyle 5.29 \times 10^{-11} \)) meters. That’s small—about 50,000 times smaller than the width of a human hair!

Why is this important? Well, Bohr’s radius gives us a scale to understand the size of atoms and the distances involved in atomic structures. It’s a fundamental concept that helps us visualize how tiny atoms are and how the electrons are arranged with the nucleus.

Bohr’s radius is the average distance from the nucleus to the electron in the ground state of a hydrogen atom. To derive it, we’ll use a few fundamental principles and constants:

This is the force of attraction between the positively charged nucleus and the negatively charged electron. It’s given by Coulomb’s law:

\(\displaystyle F_{electrostatic} = \frac{k \cdot e^2}{r^2} \)

Here,(k) is Coulomb’s constant, (e) is the charge of the electron, and (r) is the distance between the nucleus and the electron.

For the electron to move in a circular orbit, it needs a centripetal force, which is provided by the electrostatic force. The centripetal force is given by:

\(\displaystyle F_{centripetal} = \frac{m_e \cdot v^2}{r} \)

(m_e) is the mass of the electron, and (v) is the velocity of the electron.

Since the electrostatic force provides the necessary centripetal force for the electron’s circular motion, we can set these two forces equal to each other:

\(\displaystyle\frac{k \cdot e^2}{r^2} = \frac{m_e \cdot v^2}{r} \)

According to Bohr’s model, the angular momentum of the electron is quantized and is an integral multiple of ( \(\displaystyle\frac{h}{2\pi} \)), where (h) is Planck’s constant. The angular momentum (L) is given by:

\(\displaystyle L = m_e \cdot v \cdot r = n \cdot \frac{h}{2\pi} \)

Here, (n) is the principal quantum number, and for the ground state, (n = 1).

Now, let’s combine these equations to solve for (r), the Bohr radius.

From the quantization of angular momentum:

\(\displaystyle v = \frac{n \cdot h}{2\pi \cdot m_e \cdot r} \)

Substitute (v) into the centripetal force equation:

\(\displaystyle \frac{k \cdot e^2}{r^2} = \frac{m_e \cdot (\frac{n \cdot h}{2\pi \cdot m_e \cdot r})^2}{r} \)

Simplify and solve for (r):

\(\displaystyle r = \frac{n^2 \cdot h^2}{4\pi^2 \cdot k \cdot m_e \cdot e^2} \)

For the ground state (n = 1), this becomes:

\(\displaystyle r = \frac{h^2}{4\pi^2 \cdot k \cdot m_e \cdot e^2} \)

However, to express this in terms of the permittivity of free space ( \(\displaystyle\varepsilon_0 \)), we use the relation ( \(\displaystyle k = \frac{1}{4\pi \varepsilon_0} \)). Substituting this into our expression for (r), we get:

\(\displaystyle r = \frac{h^2 \cdot \varepsilon_0}{\pi \cdot m_e \cdot e^2} \)

This shows that Bohr’s radius depends on Planck’s constant, the permittivity of free space, the mass of the electron, and the charge of the electron. It’s a fundamental constant that gives us the scale of the hydrogen atom in its ground state.

When an electron moves away from Bohr’s radius, it is moving to a higher energy level, which means it is absorbing energy. This is often due to an external energy source, like a photon, that provides the necessary energy for the electron to ‘jump’ up to a higher orbit. As the electron moves to a larger orbit, its potential energy increases because it’s getting further from the nucleus, which has a positive charge that attracts the negatively charged electron.

Conversely, when an electron moves closer to Bohr’s radius, it drops to a lower energy level thus releasing energy. This released energy is usually in the form of a photon, a particle of light. The closer the electron is to the nucleus, the more tightly it is bound by the nucleus’s positive charge, and the lower its potential energy.

These movements of electrons between different orbits or energy levels are what give rise to the emission or absorption spectra of atoms. When electrons absorb energy and move to higher energy levels, they can later release this energy as they fall back down, emitting light at specific wavelengths that correspond to the energy differences between the levels. This is how we get the characteristic lines in the atomic spectra of elements. The concept of quantization in Bohr’s model explains why these lines are discrete and not a continuous spectrum.

Postulates of Bohr Model of Hydrogen Atom

Bohr’s First Postulate

Electrons orbit in stable, discrete orbits without emitting radiation. This postulate is about the electron’s ‘comfort zone’ around the nucleus where it can stay indefinitely without any energy loss, which was a novel concept at the time Bohr introduced his model.

Imagine you’re at a track field, and there are specific lanes you’re allowed to run in. You can’t just run anywhere; you have to stick to your lane. In the Bohr Model, electrons behave similarly. They orbit the nucleus in specific ‘lanes’ or orbits, and as long as they stay in their lane, they don’t lose energy by emitting radiation.

Bohr proposed that these orbits are stable, which means that an electron in one of these orbits won’t spiral into the nucleus or drift away. It’s like running in a lane with invisible walls that keep you from moving inwards or outwards. This was a big deal because, according to classical physics, moving electrons should emit energy and eventually crash into the nucleus, but that doesn’t happen.

So, in Bohr’s view, an electron in a hydrogen atom can circle the nucleus forever in one of these orbits without ever losing energy. It’s only when the electron jumps to a different orbit that it will absorb or emit energy, but that’s a story for another time.

This postulate was revolutionary because it introduced the idea of quantization in orbits, meaning that not all orbits are possible—only certain ones where the electron is stable and doesn’t radiate energy. It’s a bit like having a playlist with only your favorite songs that you can listen to on repeat without getting bored or needing to change the tune.

Bohr’s Second Postulate

The angular momentum of an electron in orbit is quantized and is an integral multiple of (\(\displaystyle n\frac{h}{2\pi} \)). Bohr’s second postulate is about the ‘dance’ of electrons around the nucleus. Just like dancers who can only spin at certain speeds when they’re performing a routine, electrons can only orbit the nucleus with specific amounts of angular momentum.

Angular momentum is a measure of how much ‘oomph’ an object has while it’s spinning or orbiting. For an electron, this ‘oomph’ is not just any amount; it has to be a whole number multiple of a very tiny number divided by (\(\displaystyle 2\pi \)) (which is roughly 6.28). This tiny number is Planck’s constant (h), which is about (\(\displaystyle 6.6 \times 10^{-34} \)) joule-seconds.

So, according to Bohr, the angular momentum (L) of an electron in its orbit is given by:

\(\displaystyle L = n\frac{h}{2\pi} \)

Here, (n) is a whole number (1, 2, 3, and so on), and it tells us which ‘dance move’ the electron is doing. If (n) is 1, the electron is doing the simplest move, and as (n) gets bigger, the moves get more complex.

This idea of quantized angular momentum is like saying the electron can only have certain ‘allowed’ spins. It can’t just spin at any speed; it has to follow the rules of this quantum dance. This keeps the electron in stable orbits and prevents it from losing energy and spiraling into the nucleus.

In essence, Bohr’s second postulate introduces a rule to the electron’s movement, providing a discrete set of possibilities for its ‘dance’ around the nucleus, which is a key concept in understanding the behavior of atoms.

Bohr’s Third Postulate

Energy is emitted or absorbed when an electron transitions between orbits, in discrete amounts called quanta. Think of an electron as a little energy packet whizzing around the nucleus in its special track. According to Bohr, these tracks or orbits are like the rungs of a ladder. An electron can jump from one rung to another, but it can’t just float between them.

Now, when an electron jumps down to a lower rung (closer to the nucleus), it loses some energy. This lost energy doesn’t just disappear; it gets released as a tiny packet of light called a photon. The energy of this photon is the same as the energy difference between the two rungs (orbits) the electron jumped between.

Here’s the cool part: the energy of the photon determines its color. So, when an electron drops from a higher to a lower orbit, it’s like it’s choosing what color of light to emit based on how far it jumps.

The formula for this process is:

\(\displaystyle h\nu = E_{i} – E_{f} \)

• (h) is Planck’s constant, a tiny number that shows up a lot in quantum physics.
• (ν) is the frequency of the photon, which is related to its color.
• (E_i) is the energy of the electron before it jumps.
• (E_f) is the energy of the electron after it jumps.

And since (E_i) is greater than (E_f) (because the electron is losing energy), the photon’s energy is just the difference between the two.

In simpler terms, this postulate tells us that when an electron moves to a lower-energy orbit, it’s like it takes off a heavy backpack (loses energy) and throws it away as a colored light (the photon). The bigger the backpack (the more energy lost), the more energetic the color of light emitted. This is a fundamental concept that helps explain why we see specific colors in things like fireworks or neon signs.

Energy Levels

The energy levels represent the fixed energies that an electron can have within an atom. Energy levels in a hydrogen atom are like the floors in a building where an electron can live. Just as you can’t stand between two floors in a building, an electron can’t exist between two energy levels.

The further the electron is from the nucleus, the higher the energy level and the more energy the electron has.

Each energy level is assigned a number called the principal quantum number, denoted by (n). For the ground state, (n = 1). For the first excited state, (n = 2), and so on. The energy of each level is related to this number.

When an electron changes energy levels, it doesn’t just slide up or down smoothly. It makes a quantum leap, instantly jumping from one level to another without passing through the space in between. Energy levels are the distinct ‘floors’ where an electron can be found, and they define the electron’s potential energy within the atom.

Quantized Orbits: Electrons can only exist in these quantized orbits or energy levels, and not in between. This means that an electron’s energy is also quantized; it can only have certain values.

The energy levels closer to the nucleus are lower in energy and more stable. Electrons naturally tend to occupy the lowest available energy level, known as the ground state. When an electron absorbs energy, it can move to a higher energy level or an excited state. This is like climbing up the staircase to a higher step. The electron in an excited state is less stable and tends to fall back to a lower energy level, releasing energy in the process.

The transition of an electron from a higher to a lower energy level results in the emission of a photon. The energy of this photon corresponds to the difference in energy between the two levels. This is why hydrogen emits light at specific wavelengths when excited.

If an electron gains enough energy, it can escape the atom entirely, a process known as ionization. The energy required to remove the electron from the ground state to infinity is called the ionization energy. Energy levels dictate how electrons behave in a hydrogen atom, influencing their stability, interactions with light, and chemical reactivity.

Absorption and Emission

Absorption and emission are like the steps an electron takes up and down its energy ladder. Absorption is the step-up, powered by incoming energy, and emission is the step-down, releasing energy as light. These processes explain why we see specific colors in things like neon lights or the sun’s spectrum.

Absorption: Absorption happens when an electron in an atom takes in energy from light (or another source). This energy boost allows the electron to jump from a lower energy level to a higher one. It’s like climbing up a ladder; you need extra energy to move up to the next rung. In the atom, when the light of just the right color (which corresponds to a specific energy) hits the electron, the electron absorbs that energy and moves to a higher “step” on its energy ladder.

Emission: Emission is the opposite of absorption. After an electron has absorbed energy and moved to a higher energy level, it won’t stay there forever. It’s unstable, like being on a ladder and wanting to come back down to the ground. So, the electron will eventually lose that extra energy and fall back to a lower energy level. When it does this, it emits energy in the form of light. The color of this light depends on the difference in energy between the two levels the electron jumps between.

Also Read: Rutherfords Alpha Scattering Experiment

Limitations of Bohr Model of Hydrogen Atom

The Bohr Model was a significant step forward in our understanding of atomic structure, but it has its limitations.

• Limited to Hydrogen-like Atoms: The Bohr Model works well for hydrogen, which has only one electron, but it doesn’t work for atoms with more than one electron. This is because it doesn’t account for the interactions between multiple electrons.
• Spectral Lines Not Fully Explained: While the Bohr Model could explain the positions of the spectral lines for hydrogen, it couldn’t explain their relative intensities or the fine structure of the spectral lines. This means it couldn’t show why some lines are brighter or more intense than others.
• Electron Wave Behavior: The model treats electrons as particles in fixed orbits, but it doesn’t consider their wave-like properties. Later developments in quantum mechanics showed that electrons have properties of both particles and waves, which the Bohr Model doesn’t address.
• Lack of Generalization: Bohr’s Model is not a general theory that can be applied to all elements. It’s a specific solution for the hydrogen atom and doesn’t extend to the broader periodic table.
• Quantum Mechanics: The Bohr Model predates modern quantum mechanics. It doesn’t incorporate the Heisenberg Uncertainty Principle, which states that you can’t know both the position and velocity of an electron with absolute certainty.

The Bohr Model was groundbreaking at the time, it’s now seen as a stepping stone towards the more complete and complex theories of quantum mechanics that we use today.

Solved Examples

Problem 1: Calculate the radius of the second orbit (n=2) of the hydrogen atom using Bohr’s model. (Given: (\(\displaystyle \epsilon_0 = 8.85 \times 10^{-12}, \text{C}^2/\text{N·m}^2 \)), (\(\displaystyle e = 1.6 \times 10^{-19} \, \text{C} \)), (\(\displaystyle m_e = 9.11 \times 10^{-31} \, \text{kg} \)), (\(\displaystyle h = 6.63 \times 10^{-34} \, \text{Js} \)).

Solution: The radius of the (n)^-th orbit in a hydrogen atom is given by:

\(\displaystyle r_n = \frac{n^2 h^2 \epsilon_0}{\pi m_e e^2}\)

Substitute the given values for (n = 2):

\(\displaystyle r_2 = \frac{2^2 \times (6.63 \times 10^{-34})^2 \times 8.85 \times 10^{-12}}{\pi \times 9.11 \times 10^{-31} \times (1.6 \times 10^{-19})^2}\)

\(\displaystyle r_2 = \frac{4 \times 4.39 \times 10^{-67} \times 8.85 \times 10^{-12}}{3.14 \times 9.11 \times 10^{-31} \times 2.56 \times 10^{-38}}\)

\(\displaystyle r_2 = \frac{1.55 \times 10^{-77}}{7.30 \times 10^{-69}} = 2.12 \times 10^{-8} \, \text{m}\)

The radius of the second orbit of the hydrogen atom is (\(\displaystyle 2.12 \times 10^{-8} \, \text{m} \)).

Problem 2: Calculate the energy of an electron in the third orbit (n=3) of a hydrogen atom using Bohr’s model.

Solution: The energy of an electron in the (n)^-th orbit of a hydrogen atom is given by:

\(\displaystyle E_n = -\frac{13.6 \, \text{eV}}{n^2}\)

Substitute (n = 3):

\(\displaystyle E_3 = -\frac{13.6}{3^2} = -\frac{13.6}{9} = -1.51 \, \text{eV}\)

The energy of an electron in the third orbit of a hydrogen atom is (-1.51 eV).

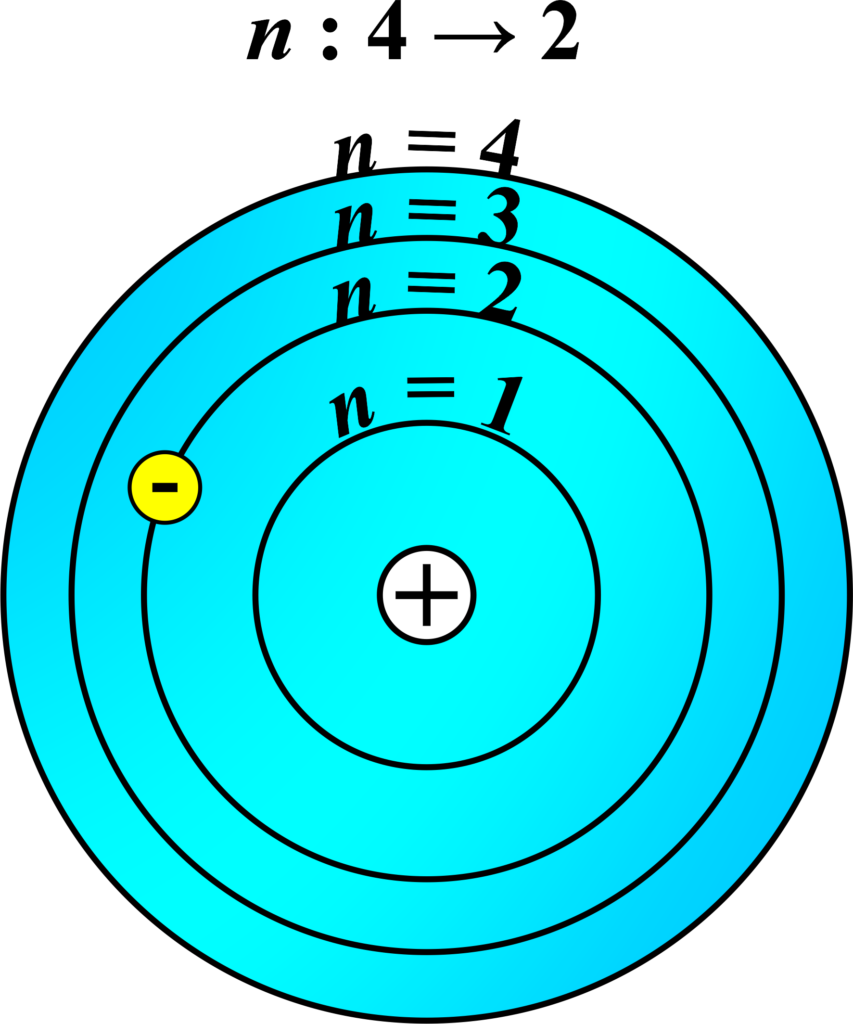
Problem 3: Calculate the photon’s wavelength when an electron transitions from the second orbit (n=2) to the first orbit (n=1) in a hydrogen atom.

Solution: The energy difference between the two orbits is given by:

\(\displaystyle\Delta E = E_1 – E_2 = -13.6 \left( \frac{1}{1^2} – \frac{1}{2^2} \right) \, \text{eV}\)

\(\displaystyle\Delta E = -13.6 \left( 1 – \frac{1}{4} \right) = -13.6 \left( \frac{3}{4} \right) = -10.2 \, \text{eV}\)

The relation gives the wavelength (λ) of the emitted photon:

\(\displaystyle\Delta E = \frac{hc}{\lambda}\)

Rearranging for (λ):

\(\displaystyle\lambda = \frac{hc}{\Delta E}\)

Substitute (\(\displaystyle h = 6.63 \times 10^{-34} \, \text{Js} \)), (\(\displaystyle c = 3 \times 10^8 \, \text{m/s} \)), and ( \(\displaystyle\Delta E = 10.2 \, \text{eV} = 10.2 \times 1.6 \times 10^{-19} \, \text{J} \)):

\(\displaystyle\lambda = \frac{6.63 \times 10^{-34} \times 3 \times 10^8}{10.2 \times 1.6 \times 10^{-19}}\)

\(\displaystyle\lambda = \frac{1.989 \times 10^{-25}}{1.632 \times 10^{-18}} = 1.22 \times 10^{-7} \, \text{m} = 122 \, \text{nm}\)

The wavelength of the photon emitted during the transition from the second to the first orbit is (122 nm).

Problem 4: Calculate the frequency of the photon absorbed when an electron in a hydrogen atom transitions from the ground state (n=1) to the second excited state (n=3).

Solution: The energy difference between the two orbits is given by:

\(\displaystyle\Delta E = E_3 – E_1 = -13.6 \left( \frac{1}{3^2} – 1 \right) \, \text{eV}\)

\(\displaystyle\Delta E = -13.6 \left( \frac{1}{9} – 1 \right) = -13.6 \left( \frac{1 – 9}{9} \right) \)

\(\displaystyle = 13.6 \left( \frac{8}{9} \right) = 12.09 \, \text{eV}\)

The frequency (ν) of the absorbed photon is given by:

\(\displaystyle\Delta E = h\nu\)

Rearranging for (ν):

\(\displaystyle\nu = \frac{\Delta E}{h}\)

Substitute ( \(\displaystyle\Delta E = 12.09 \, \text{eV} = 12.09 \times 1.6 \times 10^{-19} \, \text{J} \)) and ( \(\displaystyle h = 6.63 \times 10^{-34} \, \text{Js} \)):

\(\displaystyle \nu = \frac{12.09 \times 1.6 \times 10^{-19}}{6.63 \times 10^{-34}} = \frac{19.344 \times 10^{-19}}{6.63 \times 10^{-34}} \)

\(\displaystyle = 2.92 \times 10^{15} \, \text{Hz}\)

The frequency of the photon absorbed during the transition from the ground state to the second excited state is (\(\displaystyle 2.92 \times 10^{15} \, \text{Hz} \)).

Problem 5: Determine the kinetic energy of an electron in the first orbit of a hydrogen atom using Bohr’s model.

Solution: In Bohr’s model, the kinetic energy (KE) of an electron in the (n)^-th orbit is given by:

\(\displaystyle KE = -\frac{E_n}{2}\)

For (n = 1):

\(\displaystyle E_1 = -13.6 \, \text{eV}\)

So,

\(\displaystyle KE = -\frac{-13.6}{2} = 6.8 \, \text{eV}\)

The kinetic energy of an electron in the first orbit of a hydrogen atom is ( 6.8 eV).

Problem 6: Calculate the total energy of an electron in the fourth orbit (n=4) of the hydrogen atom.

Solution: The total energy of an electron in the (n)-th orbit of a hydrogen atom is given by:

\(\displaystyle E_n = -\frac{13.6 \, \text{eV}}{n^2}\)

Substitute (n = 4):

\(\displaystyle E_4 = -\frac{13.6}{4^2} = -\frac{13.6}{16} = -0.85 \, \text{eV}\)

The total energy of an electron in the fourth orbit of a hydrogen atom is ( -0.85 eV).

FAQs