Long ago, in the early 1600s, a curious scientist named Galileo Galilei made an unusual observation inside a large cathedral in Italy. As he sat watching a chandelier swinging gently from the ceiling, he noticed something fascinating — the time it took for the chandelier to swing back and forth remained nearly the same, even as the swing became smaller. This caught his attention. Using nothing more than his own pulse to measure time, Galileo began to understand that this regular, repetitive motion had a pattern. Though he didn’t yet call it “simple harmonic motion”, Galileo had stumbled upon one of the most important principles in physics — periodic motion.
Galileo’s interest didn’t stop there. He experimented further with pendulums and found that for small swings, the time period depends only on the length of the pendulum and not on how far it swings. This idea became the foundation for using pendulums in clocks, bringing more accuracy to timekeeping than ever before. For the first time in history, scientists were beginning to measure time using nature’s rhythm.
A few decades later, another brilliant mind, Robert Hooke, entered the scene. He was fascinated by springs and elasticity. In 1676, Hooke discovered that the force needed to stretch or compress a spring is directly proportional to the displacement. He summarized this idea with a simple but powerful equation: F = -kx
This was called Hooke’s Law, and it introduced the concept of a restoring force — a force that always pulls an object back toward its original position. Though Hooke was not directly talking about SHM, his discovery laid the mechanical groundwork for it. The idea that a system could continuously be pulled back toward equilibrium set the stage for understanding oscillations more deeply.
Then came Isaac Newton, the father of classical physics. In his monumental work Principia Mathematica (published in 1687), Newton provided the laws of motion and applied them to various physical systems. He used calculus to explain how objects move and accelerate. When Newton looked at systems like pendulums and springs, he connected the ideas of force and acceleration. He showed mathematically that when a particle is pulled back by a force proportional to its displacement (like Hooke described), the particle undergoes simple harmonic motion. This was a turning point — now SHM wasn’t just an observation or an experiment. It was a motion that could be described precisely using mathematics and physics laws.
As time passed and the 1800s approached, another great mind, Jean-Baptiste Joseph Fourier, took the study of motion even further. Fourier showed that any repeating (periodic) motion, no matter how complex, could be broken down into simple sine and cosine waves — the very functions that describe SHM. This was revolutionary. Whether it was the vibration of a violin string, the sound of someone’s voice, or ripples in water, they could all be analyzed using simple harmonic components. His work connected SHM not just to mechanics, but to music, sound, and light — shaping entire fields like acoustics and signal processing.
As we moved into the 20th century, the concept of SHM became even more powerful. Scientists realized that molecules vibrate in SHM patterns, that electrons oscillate in atoms, and that radio waves travel as electromagnetic oscillations. Even buildings and bridges were analyzed for resonance, which is directly linked to SHM — engineers needed to be sure that a building wouldn’t collapse if its natural frequency matched the vibrations caused by wind or an earthquake.
One famous example is the Tacoma Narrows Bridge in the USA, which collapsed in 1940. The bridge started swaying violently because strong winds matched the bridge’s natural frequency — a deadly demonstration of resonance, a direct application of SHM.
Key Terms
Periodic Motion: This is any motion that repeats itself at regular intervals of time. Examples include uniform circular motion, the orbital motion of planets, or even the bouncing of a ball between your hand and the ground (though the graph of its height versus time might look a bit different). The smallest interval of time after which the motion repeats is called its period (T). Its SI unit is the second.
Frequency (ν): This is the reciprocal of the period (T) and represents the number of repetitions that occur per unit time. The relationship is ν = 1/T. The unit of frequency is s⁻¹, also called hertz (Hz), where 1 Hz = 1 oscillation per second. Frequency is not necessarily an integer.
Oscillatory Motion: This is a type of periodic motion where an object moves to and fro about a mean position. This mean position is often an equilibrium position where no net external force acts on the body. If displaced slightly from this position, a force tries to bring the body back, causing oscillations or vibrations. Examples include a pendulum of a wall clock, a ball in a bowl, or leaves oscillating in the breeze.
Now, while every oscillatory motion is periodic, not every periodic motion needs to be oscillatory. For example, circular motion is periodic but not oscillatory.
Simple Harmonic Motion (SHM)
SHM is described as the simplest form of oscillatory motion. The key characteristic defining SHM relates to the force acting on the oscillating body:
- In SHM, the force on the body is directly proportional to its displacement from the mean position, which is also the equilibrium position.
- Furthermore, this force is always directed towards the mean position. This type of force is called a restoring force.
- This force law can be expressed mathematically as F(t) = -k x(t), where F is the force, x is the displacement from the mean position, and k is a constant. The negative sign indicates that the force is always opposite in direction to the displacement, pulling or pushing the particle back towards the equilibrium point (x=0).
- A system where the restoring force is proportional to the displacement (F = -kx) is also referred to as a linear harmonic oscillator.
Mathematical Description of SHM
In SHM, the restoring force always tries to bring the object back to its mean position, and is proportional to the displacement.
\(\displaystyle F \propto -x \)
The negative sign shows that the direction of the force is opposite to the displacement.
Introducing a constant of proportionality kk, we write:
\(\displaystyle F = -k x \tag{1}\)
From Newton’s second law of motion:
\(\displaystyle F = m a = m \frac{d^2x}{dt^2} \tag{2}\)
Where:
- m = mass of the object
- \(\displaystyle \frac{d^2x}{dt^2} \)= acceleration
Combine Equations (1) and (2), Equating both expressions for force:
\(\displaystyle m \frac{d^2x}{dt^2} = -k x\)
Divide both sides by m:
\(\displaystyle\frac{d^2x}{dt^2} + \frac{k}{m} x = 0 \tag{3}\)
Let: \(\displaystyle\omega^2 = \frac{k}{m}\)
Now equation (3) becomes:
\(\displaystyle \frac{d^2x}{dt^2} + \omega^2 x = 0 \tag{4}\)
This is the standard differential equation of SHM.
General Solution of the Differential Equation, The solution of this second-order differential equation is:
\(\displaystyle x(t) = A \cos(\omega t) + B \sin(\omega t) \tag{5}\)
Where:
- A and B are constants (depend on initial conditions)
- \(\displaystyle\omega\) = angular frequency
- t = time
This is the general form of SHM. Express in a Single Cosine Function, Using trigonometric identity, this expression can also be written as:
\(\displaystyle x(t) = C \cos(\omega t + \phi) \tag{6}\)
Where:
- C = amplitude = \(\displaystyle \sqrt{A^2 + B^2}\)
- \(\displaystyle \phi \)= phase constant = \(\displaystyle\tan^{-1} \left( -\frac{B}{A} \right)\)
Final Equation of SHM,
\(\displaystyle x(t) = A \cos(\omega t + \phi)\)
Where:
- x(t) = displacement at time tt
- A = amplitude
- ω= angular frequency =\(\displaystyle\sqrt{\frac{k}{m}}\)
- ϕ = phase constant
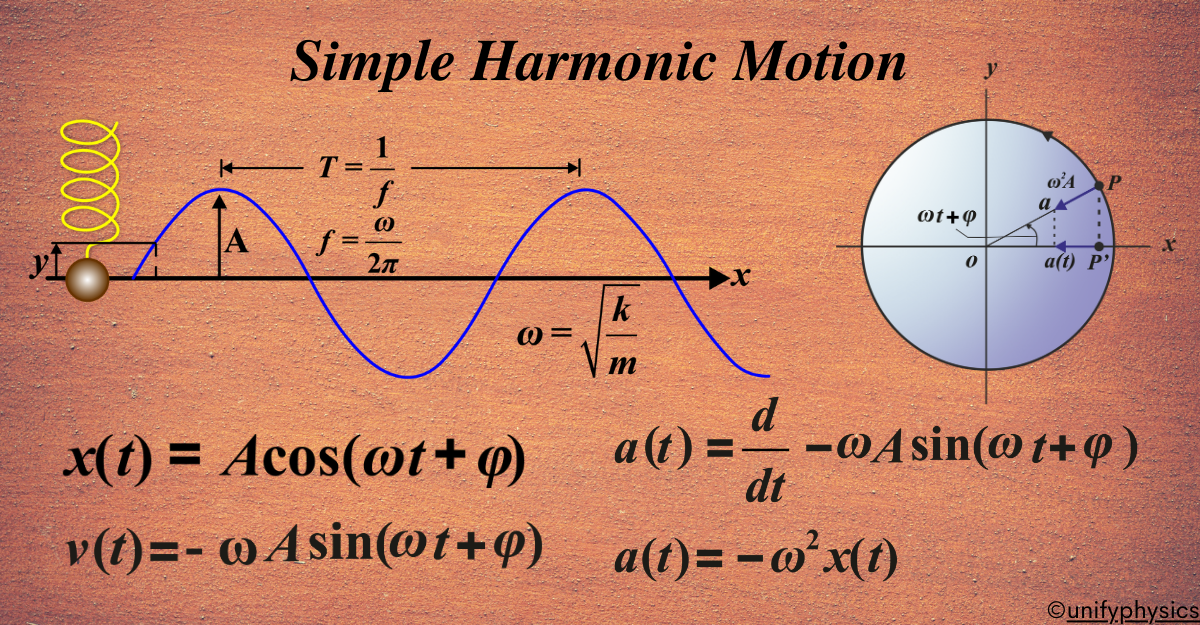
The displacement of a particle undergoing linear simple harmonic motion can be represented by a sinusoidal function of time. One common form is:
x(t) = A cos (ωt + φ)
- x(t): This is the displacement of the particle from its equilibrium position at a given time t. Displacement here is used in a general sense, referring to the change in the physical property under consideration over time, not just position. It can take both positive and negative values.
- A: This is the Amplitude of the motion. It is a positive constant representing the magnitude of the maximum displacement of the particle in either direction from the mean position.
- (ωt + φ): This entire quantity is called the phase of the motion. It describes the state of motion at a given time.
- φ: This is the phase constant (or phase angle). It’s a constant value that depends on the initial conditions of the motion (displacement and velocity at t=0). It signifies the initial conditions.
- ω: This is the angular frequency of the motion. It is related to the period T by the equation ω = 2π/T. Its SI unit is radians per second. The angular frequency is also related to the spring constant (k) and mass (m) in a linear oscillator by ω = √(k/m).
The function f(t) = A cos(ωt + φ) is periodic with period T = 2π/ω. Similarly, f(t) = A sin(ωt) or a linear combination like f(t) = A sin(ωt) + B cos(ωt) are also periodic with the same period T. Notably, any periodic function can be expressed as a superposition of sine and cosine functions of different time periods.
Velocity and Acceleration in SHM
Velocity in SHM
In simple harmonic motion (SHM), an object moves back and forth around a central point (called the mean position). You already know that its displacement changes with time in a wave-like pattern. But how fast does it move at each point? That’s where velocity comes in — and it behaves in a very interesting way.
Let’s say you have a mass attached to a spring, and you pull it to one side and release it. The mass starts oscillating — moving to and fro. When the mass reaches the end points (maximum displacement, or amplitude), it stops for a moment before reversing direction. That means its velocity is zero at the extreme positions.
As it starts coming back towards the center, it speeds up. At the mean position, the object is moving the fastest. So, in SHM:
- Velocity is maximum at the mean position
- Velocity is zero at the extreme positions
We already know that in SHM, displacement is given by:
\(\displaystyle x(t) = A \cos(\omega t + \phi)\)
To find velocity, we take the derivative of displacement with respect to time:
\(\displaystyle v(t) = \frac{dx}{dt} = -A \omega \sin(\omega t + \phi)\)
So, the equation for velocity becomes:
\(\displaystyle v(t) = -\omega A \sin(\omega t + \phi)\)
This tells us how velocity varies with time. The negative sign shows that the direction of velocity is opposite to that of displacement when moving toward the mean position.
Velocity in terms of displacement: Using energy conservation and trigonometry, we can also write velocity as:
\(\displaystyle v = \omega \sqrt{A^2 – x^2}\)
This form helps us understand that velocity depends on how far the particle is from the mean position. When x = A or -A, velocity is 0. When x = 0, velocity is maximum, \(\displaystyle v_{\text{max}} = \omega A\)
Graphical Understanding
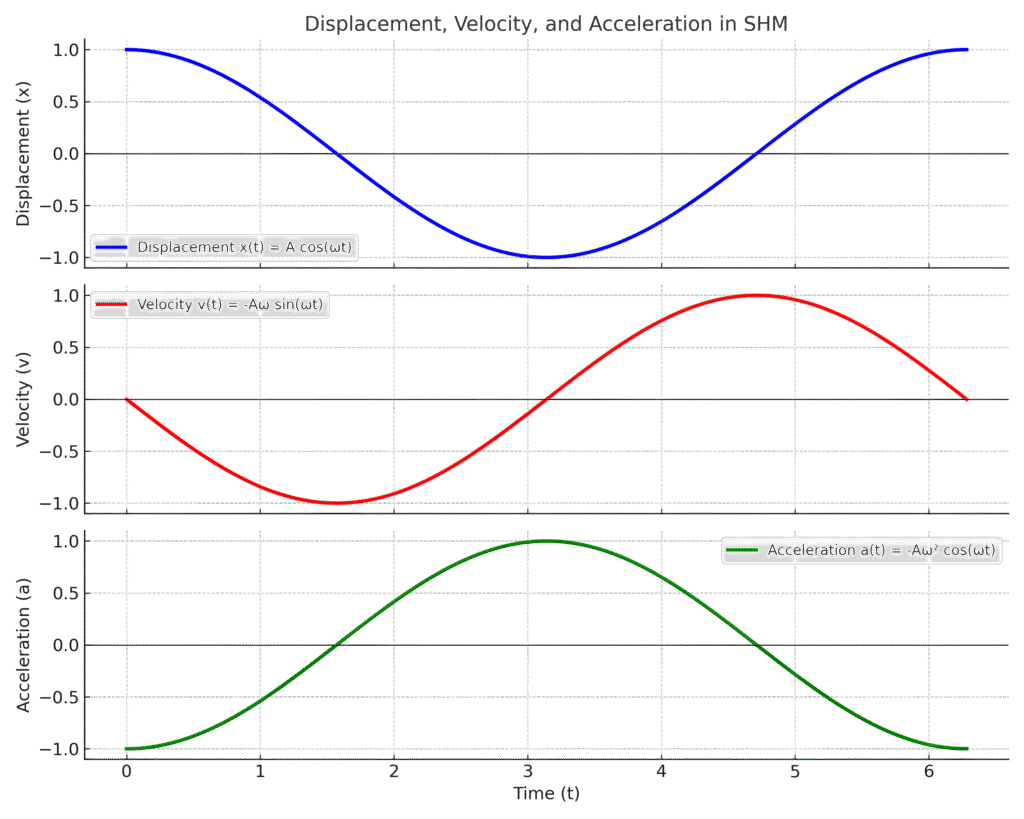
Interpretation of the Graphs:
- The displacement graph is a cosine wave.
- The velocity graph is a sine wave (with negative sign).
- Notice that the velocity wave is shifted by a quarter cycle (π/2 radians) from the displacement wave.
- At the peak of displacement, velocity is zero.
- At zero displacement (mean position), velocity is maximum.
Physical Meaning: Let’s relate this to real life. Imagine pushing a child on a swing:
- At the highest point (extreme position), the child momentarily stops — zero velocity.
- As they come down toward the center, they speed up — velocity increases.
- At the bottom (mean position), they’re moving the fastest — maximum velocity.
- Then, as they rise again, they slow down — velocity decreases — and becomes zero at the next extreme.
This is exactly how velocity behaves in SHM.
The instantaneous velocity v(t) of a particle in SHM is given by the first derivative of the displacement x(t): v(t) = -ωA sin (ωt + φ) The maximum speed (velocity amplitude) is vm = ωA. The velocity of the oscillating particle varies between ±ωA. The velocity lags behind the displacement by a phase angle of π/2. Velocity is zero at the extreme positions (maximum displacement) and maximum when the particle is at the mean position (zero displacement).
Acceleration in SHM
When we talk about motion, we usually think about how fast something moves — that’s velocity. But in simple harmonic motion (SHM), there’s another important aspect to understand: acceleration. In SHM, acceleration plays a special role because it is directly responsible for the motion.
Let’s imagine a mass hanging from a spring, or a pendulum swinging from side to side. These objects go back and forth repeatedly — they oscillate. At every moment, there’s a force acting on them that tries to pull them back toward the central position, called the mean position. This force is called a restoring force, and it is always trying to bring the object back to equilibrium.
Now, according to Newton’s Second Law, force causes acceleration: F = ma. But in SHM, the force itself depends on how far the object is from the center. That’s given by: F = -kx
Combining these two, we get:
\(\displaystyle ma = -kx \quad \Rightarrow \quad a = -\frac{k}{m}x\)
We introduce angular frequency ω; where: \(\displaystyle\omega^2 = \frac{k}{m}\)
Now, we can write the acceleration in SHM as:
\(\displaystyle a(t) = -\omega^2 x(t)\)
This equation tells us two very important things:
- Acceleration is directly proportional to displacement — if you double the displacement, acceleration doubles.
- The negative sign means the direction of acceleration is always opposite to displacement — if the object is to the right, the acceleration is to the left.
What does this mean during motion?
- When the object is at the maximum displacement (farthest from center), the acceleration is maximum because it’s being pulled back strongly.
- When the object passes through the mean position, the displacement is zero, so acceleration is also zero. That’s because no force is acting to pull it back at that exact moment — but it’s moving the fastest here!
- As it moves to the opposite side, the acceleration changes direction, still pointing toward the center.
So, acceleration in SHM is like a push that gets stronger as the object moves away from the center, and reverses direction every time the object crosses the mean position.
The instantaneous acceleration a(t) is given by the first derivative of the velocity v(t) or the second derivative of the displacement x(t): a(t) = -ω²A cos (ωt + φ) Substituting x(t) = A cos(ωt + φ), we get the important relationship: a(t) = -ω²x(t) This shows that in SHM, the acceleration is proportional to the displacement and is always directed towards the mean position. The maximum acceleration (acceleration amplitude) is am = ω²A. When displacement is maximum positive, acceleration is maximum negative, and vice versa. When displacement is zero, acceleration is also zero.
SHM and Uniform Circular Motion
To understand Simple Harmonic Motion (SHM) more deeply, it helps to explore a surprising yet beautiful idea: SHM is just a shadow of uniform circular motion. This connection was first noticed by Galileo, and later developed into a powerful mathematical model that helps us visualize and understand oscillations in a new way. Galileo observed the moons of Jupiter appearing to move back and forth in SHM relative to the planet, and it is now known that they move in nearly circular orbits. What he saw was the projection of their uniform circular motion.
Let’s begin with a simple setup. Imagine a particle moving in a uniform circular motion — that means it is going around a circle at a constant speed. Suppose this motion happens in a horizontal circle, like a stone tied to a string and whirled in a perfect circle. Now, imagine watching this motion from the side — from a point where you can only see the projection of the particle on a wall behind it. What you see is not a circle, but rather a to-and-fro motion — the particle appears to move back and forth in a straight line. This back-and-forth projection of circular motion is exactly what we call Simple Harmonic Motion.
Consider a particle moving in a circle of radius A with constant angular velocity ω. At any time t, the position of the particle makes an angle θ = ωt with the horizontal axis. If we project the position of the particle onto the horizontal diameter of the circle, we get:
\(\displaystyle x(t) = A \cos(\omega t)\)
This is the exact equation of displacement for SHM. So, the horizontal projection of the circular motion follows a cosine wave — just like a mass on a spring or a pendulum swinging back and forth.
Let’s go further. In circular motion, although the speed is constant, the direction of motion changes continuously, which means the particle has acceleration (called centripetal acceleration) pointing toward the center of the circle. When we observe the projection of this acceleration along the diameter, we get:
\(\displaystyle a(t) = -\omega^2 x(t)\)
This is also the defining equation for acceleration in SHM. So, what does this mean? It means that we can treat SHM as a one-dimensional slice or shadow of a uniform circular motion. The oscillating mass on a spring moves just like the horizontal projection of a particle moving uniformly around a circle.
This connection isn’t just a mathematical trick — it’s an extremely helpful way to visualize SHM. It helps us understand phase angles (the angle in circular motion becomes the phase in SHM), the idea of amplitude (the radius of the circle), and the smooth, wave-like nature of oscillatory motion.
To imagine this in real life, think of how the moon appears to move across the sky — though it’s moving in a circular orbit, from our point of view on Earth, it seems to move back and forth in a regular way. Similarly, if you spin a ball tied to a string in a circle and observe its shadow on a wall, the shadow will oscillate just like a mass in SHM.
Energy in SHM
To understand the energy in simple harmonic motion (SHM), let’s imagine a simple system: a mass mm attached to a spring on a smooth horizontal surface. When you pull the mass to one side and release it, it starts oscillating back and forth. While it moves, it continuously exchanges energy between potential energy (stored in the spring) and kinetic energy (due to motion). The total mechanical energy in SHM, however, always remains constant, as there is no friction or energy loss.
Let’s begin with what we know about the motion. The displacement of the object in SHM is given by the equation:
\(\displaystyle x(t) = A \cos(\omega t + \phi)\)
To find the kinetic energy, we first need the velocity of the particle. We take the derivative of displacement with respect to time:
\(\displaystyle v(t) = \frac{dx}{dt} = -A \omega \sin(\omega t + \phi)\)
Now, the kinetic energy K of the particle is given by the formula:
\(\displaystyle K = \frac{1}{2}mv^2\)
Substitute the expression of velocity into this:
\(\displaystyle K = \frac{1}{2}m (-A \omega \sin(\omega t + \phi))^2 = \frac{1}{2}m A^2 \omega^2 \sin^2(\omega t + \phi)\)
This expression shows that kinetic energy varies with time — it’s not constant. When the particle is at the mean position, the sine function becomes ±1\pm 1, and hence kinetic energy is maximum. When the particle is at the extreme position (maximum displacement), sine becomes zero, and kinetic energy is zero.
Now let’s derive the potential energy stored in the spring. In SHM, the restoring force is F = -kx, and the potential energy U stored in the spring when it is compressed or stretched by a displacement xx is given by:
\(\displaystyle U = \frac{1}{2}kx^2\)
Substitute \(\displaystyle x(t) = A \cos(\omega t + \phi)\) into this equation:
\(\displaystyle U = \frac{1}{2}k (A \cos(\omega t + \phi))^2 = \frac{1}{2}k A^2 \cos^2(\omega t + \phi)\)
Now recall that \(\displaystyle\omega^2 = \frac{k}{m}\), so we can write \(\displaystyle k = m \omega^2\). Substituting this in:
\(\displaystyle U = \frac{1}{2} m \omega^2 A^2 \cos^2(\omega t + \phi)\)
So, the potential energy also varies with time. It becomes maximum at the extreme positions (where cosine is ±1) and becomes zero at the mean position (where cosine is 0). To find the total mechanical energy E, we add kinetic and potential energy: E = K + U
\(\displaystyle E = \frac{1}{2} m A^2 \omega^2 \sin^2(\omega t + \phi) + \frac{1}{2} m A^2 \omega^2 \cos^2(\omega t + \phi)\)
Factor out the common term:
\(\displaystyle E = \frac{1}{2} m A^2 \omega^2 (\sin^2(\omega t + \phi) + \cos^2(\omega t + \phi))\)
From trigonometry, we know: \(\displaystyle \sin^2\theta + \cos^2\theta = 1\). So the total energy becomes:
\(\displaystyle E = \frac{1}{2} m A^2 \omega^2\)
This is a constant. It doesn’t depend on time. It tells us that while kinetic and potential energy in SHM keep changing from one to the other during motion, their total sum remains fixed at every moment. The energy is simply shuttling back and forth — like a perfectly coordinated dance — between movement and position, between speed and stretch. This constancy of energy is what keeps the system oscillating smoothly and predictably.
Systems Executing SHM
Oscillations Due to a Spring
One of the simplest and most common examples of a system that executes simple harmonic motion (SHM) is a spring-mass system. This setup not only helps us understand SHM clearly but also forms the foundation for studying oscillations in mechanical and physical systems.
Imagine a spring placed on a smooth horizontal table, and a block of mass mm is attached to one end of the spring. The other end of the spring is fixed to a wall. Now, if you pull the block slightly and release it, you’ll notice something interesting: the block starts to move back and forth in a rhythmic, repetitive motion. This back-and-forth motion is an example of simple harmonic motion, provided the spring obeys Hooke’s law and there’s no friction.
Let’s understand what happens when we stretch the spring. According to Hooke’s Law, the force exerted by a spring is: F = -kx
Here, x is the displacement of the mass from the equilibrium position, kk is the spring constant (which tells us how stiff the spring is), and the negative sign indicates that the force always acts in the direction opposite to the displacement — it’s a restoring force. This force is what pulls the mass back toward the mean position when it is displaced. And this is exactly the condition needed for SHM: a restoring force that is directly proportional to displacement but acts in the opposite direction.
Now, using Newton’s second law,F = ma, we can write: ma = -kx \(\displaystyle \Rightarrow a = -\frac{k}{m}x\)
This is the defining equation of SHM. It tells us that the acceleration is proportional to the negative of displacement — the more you pull the spring, the stronger the force pulling it back.
Next, let’s look at how fast the system oscillates. This depends on two things: the mass mm of the object and the stiffness kk of the spring. A heavier mass oscillates more slowly, while a stiffer spring makes the system oscillate faster. The angular frequency of oscillation is:
\(\displaystyle\omega = \sqrt{\frac{k}{m}}\)
From angular frequency, we can calculate the time period, which is the time taken to complete one full oscillation:
\(\displaystyle T = 2\pi \sqrt{\frac{m}{k}}\)
This formula shows that the time period doesn’t depend on how far you pull the spring — it only depends on the mass and the spring constant. This is why SHM is called isochronous — the time for each cycle remains the same.
To make this more visual, imagine compressing the spring and letting it go. The block moves quickly toward the mean position, gains speed, passes through the equilibrium point with maximum velocity, then slows down as the spring stretches on the other side, comes to a stop at the extreme point, and then reverses direction. This repeating motion — speeding up and slowing down — continues as long as there’s no friction to remove energy.
The same principle applies in the vertical spring system too. If you hang a mass from a vertical spring and displace it downward slightly and release, it will oscillate up and down around the new equilibrium position. The same equations apply, because gravity only shifts the equilibrium, it doesn’t affect the oscillation itself.
The Simple Pendulum
One of the most familiar examples of oscillatory motion is a simple pendulum. It’s something we’ve all seen — whether it’s the slow swinging of a hanging clock’s arm or a string with a weight at the bottom swaying gently. Though it appears very simple, the motion of a pendulum actually hides beautiful physics, and under certain conditions, it executes simple harmonic motion (SHM).
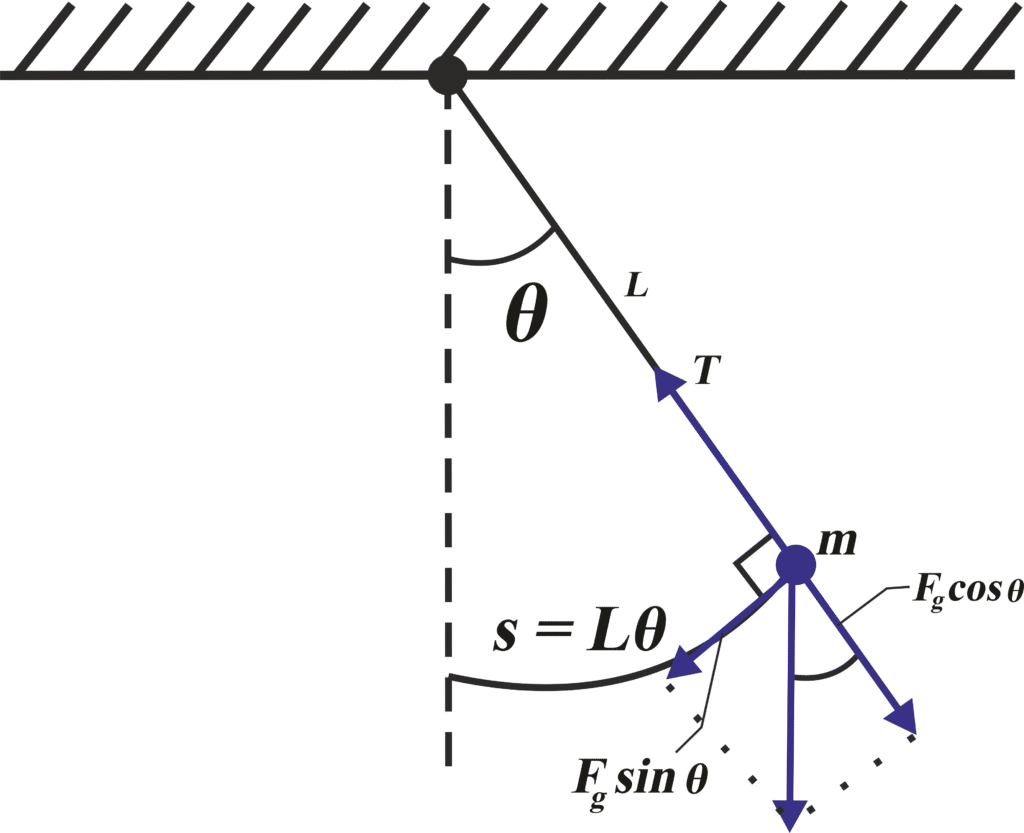
Let’s understand how. Imagine a small metal ball — called a bob — tied to a long, inextensible and massless string of length LL, suspended from a fixed support. When the bob hangs vertically downward, it’s in its equilibrium position. Now, pull the bob slightly to one side and let it go.
What happens? It swings to and fro — back and forth — through the lowest point. This motion is periodic and seems similar to SHM. But is it SHM? Let’s examine what kind of force is acting on it.
When the bob is displaced by a small angle θ a from the vertical, it experiences a restoring force due to gravity. The component of the gravitational force that causes the pendulum to return to its mean position is:
\(\displaystyle F = -mg \sin(\theta)\)
This force is always directed toward the center — toward equilibrium — and tries to bring the bob back. However, there’s a catch. SHM requires the restoring force to be directly proportional to displacement, not to the sine of an angle.
Here’s where the magic of approximation helps. For small angles (less than about 10°), we can use the mathematical approximation:
\(\displaystyle\sin(\theta) \approx \theta \quad \text{(in radians)}\)
So now the force becomes: \(\displaystyle F = -mg \theta\)
But we want this in terms of linear displacement. The arc length ss (which is how far the bob has moved along the circular path) is related to θ by:
\(\displaystyle s = L \theta \Rightarrow \theta = \frac{s}{L}\)
So the restoring force becomes: \(\displaystyle F = -mg \cdot \frac{s}{L}\)
Using Newton’s second law:
\(\displaystyle ma = -mg \cdot \frac{s}{L} \Rightarrow a = -\frac{g}{L} s\)
This is the defining equation of SHM: acceleration is directly proportional to displacement and directed toward the mean position. Hence, for small angular displacements, the motion of a simple pendulum is simple harmonic.
From this equation, we can identify the angular frequency ω:
\(\displaystyle\omega^2 = \frac{g}{L} \Rightarrow \omega = \sqrt{\frac{g}{L}}\)
And from that, the time period of one complete oscillation is: \(\displaystyle T = 2\pi \sqrt{\frac{L}{g}}\)
This is a beautiful result — the time period of a simple pendulum depends only on the length of the string and the acceleration due to gravity, and not on the mass of the bob or the amplitude (as long as the amplitude is small). So, two pendulums of the same length will swing with the same rhythm no matter what their mass is.
Also Read: Kepler’s Law of Planetary Motion