Temperature is something we all feel intuitively—hot or cold—but measuring it precisely requires a scientific approach. We’ll break this down step by step in a simple, logical order, starting with the history and building up to how we assign numerical values to temperature. I’ll use clear headings, bullet points, and equations to make it easy to follow. By the end, you’ll understand how a simple glass tube with mercury helps us quantify “hotness” or “coldness.”
Humans have always sensed temperature through touch (e.g., feeling if water is warm or ice is cold), but this is subjective and imprecise. What feels hot to one person might feel warm to another. We need objective tools to measure temperature for science, medicine, industry, and daily life—like checking body fever, monitoring weather, or ensuring safe cooking temperatures. Early attempts used basic ideas like the expansion of air or liquids with heat, but we needed a reliable scale to assign numbers (e.g., 0°C for freezing water) for consistency across experiments and locations.
The concept of thermometers dates back to the 17th century. In 1593, Galileo Galilei invented an early “thermoscope” using air expansion in a glass tube with water, but it wasn’t scaled numerically and was affected by air pressure. The mercury thermometer, as we know it, was invented in 1714 by Daniel Gabriel Fahrenheit, a German physicist. He chose mercury because of its useful properties (more on that later) and created the Fahrenheit scale.
Later, in 1742, Anders Celsius, a Swedish astronomer, proposed the Celsius (centigrade) scale, which became widely used. Mercury thermometers became standard in labs and medicine by the 18th century, revolutionizing physics and chemistry. These instruments solved the problem of quantifying temperature, allowing scientists like those studying thermodynamics to make precise measurements.
Why is Mercury Used in Thermometer?
Mercury is a shiny, silver liquid metal (the only metal that’s liquid at room temperature), and it’s ideal for thermometers for several reasons:
- Uniform Expansion: Mercury expands evenly and predictably when heated, making measurements linear and reliable over a wide temperature range (from -39°C to 357°C).
- High Visibility: It’s opaque and silvery, so the level in a thin glass tube is easy to see.
- Doesn’t Stick to Glass: It doesn’t wet the glass walls, ensuring smooth movement without residue.
- Low Freezing Point and High Boiling Point: It stays liquid in most everyday temperatures and doesn’t evaporate easily.
- Good Thermal Conductor: It quickly reaches the same temperature as its surroundings.
However, mercury is toxic, so modern thermometers often use safer alternatives like alcohol or digital sensors. But for traditional physics demos, mercury is still a classic choice!
What is a Mercury Thermometer?
A mercury thermometer is a simple device that measures temperature based on the expansion of mercury with heat. It consists of a glass bulb filled with mercury, connected to a narrow glass capillary tube (like a thin straw). The tube is sealed, and the air is removed to create a vacuum. When the bulb is heated, mercury expands and rises up the capillary tube. When cooled, it contracts and falls. The height of the mercury column indicates the temperature.
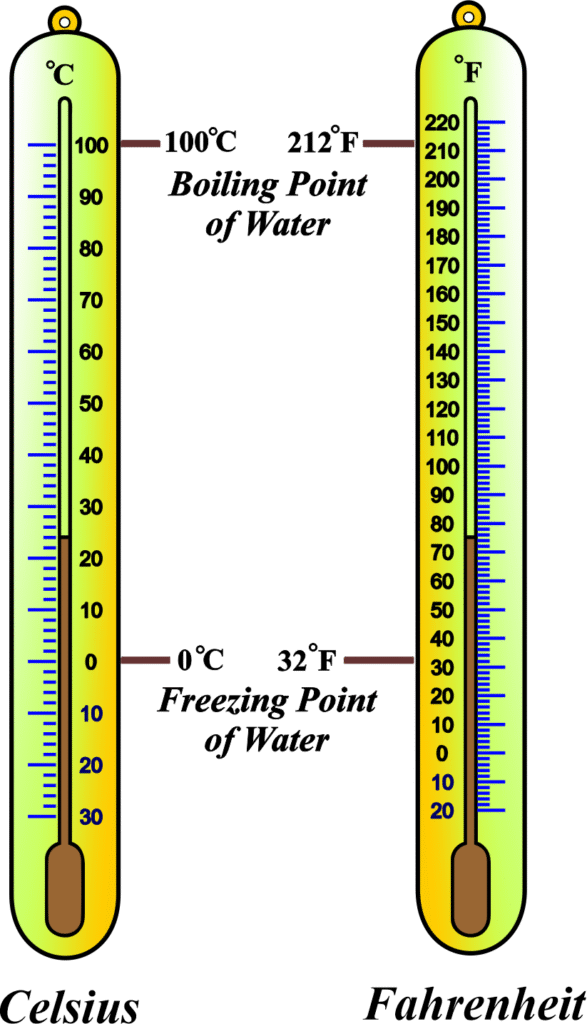
The tube is marked with a scale (e.g., Celsius or Fahrenheit) based on fixed points like the freezing and boiling points of water. Common ones include clinical thermometers (for body temperature, with a kink to hold the reading) and laboratory thermometers (straight tube for general use).
See Fig., which shows a glass tube with a bulb at the bottom, mercury inside, and scale markings along the tube. It’s a prime example of using a physical property (thermal expansion) to measure temperature.
Uses of Mercury in Everyday Life
Beyond thermometers, mercury has various practical applications (though its use is declining due to toxicity concerns):
- Electrical Switches and Relays: Mercury’s conductivity makes it useful in tilt switches (e.g., old thermostats) where it completes circuits based on position.
- Dental Fillings: Amalgam (a mercury alloy) is used in tooth fillings because it’s durable and molds well.
- Fluorescent Lamps: Mercury vapor inside bulbs produces UV light, which creates visible light (though LED alternatives are replacing them).
- Barometers: Measure air pressure using mercury columns (invented by Evangelista Torricelli in 1643).
- Batteries and Chemicals: Used in some batteries and as a catalyst in industrial processes like producing chlorine.
Always handle mercury carefully—it’s hazardous if spilled or inhaled!
Deriving the Expression for the Temperature Scale Using a Mercury Thermometer
How do we define a numerical scale for temperature using a mercury thermometer? We’ll build this step by step, assuming you’re familiar with basic thermal expansion. The goal is to assign a number (like 25°C) to the “hotness” of a body based on a measurable property.
We need a way to compare temperatures objectively. If two objects are at the same temperature, no heat flows between them (thermal equilibrium). If not, heat flows from hotter to cooler. To quantify this, pick a substance and a property that changes steadily (monotonically) with temperature. For example:
- Take some mercury in a glass bulb connected to a long, thin capillary tube.
- The property? The length of the mercury column in the tube. It increases as the temperature rises because mercury expands.
Each length corresponds to a unique temperature. But how do we assign numbers to these lengths?
Selecting Fixed Points and Assuming Linearity: Early scientists chose two reproducible “fixed points”
- Ice Point: Temperature of melting ice at 1 atm pressure (easy to make in a lab).
- Steam Point: Temperature of boiling water at 1 atm pressure.
We assign arbitrary values: say, ( t1 ) for ice point and ( t2 ) for steam point.
- Let (l1) be the mercury column length at ice point.
- Let (l2) be the length at the steam point.
Assuming the length (l) changes linearly with temperature (t) (which is a good approximation for mercury over common ranges), we can write:
\(\displaystyle t = a l + b \tag{1}\)
Here, (a) and (b) are constants we’ll find. Plug in the fixed points:
- At ice point: ( t1 = a l1 + b )
- At steam point: ( t2 = a l2 + b )
Solving these: Subtract the equations: (t2 – t1 = a (l2 – l1)) So,
\(\displaystyle a = \frac{t_2 – t_1}{l_2 – l_1} \)
Then, (b = t1 – a l1). A change of 1 degree corresponds to a length change of \(\displaystyle \frac{l_2 – l_1}{t_2 – t_1} \). We can mark the tube in equal divisions for degrees.
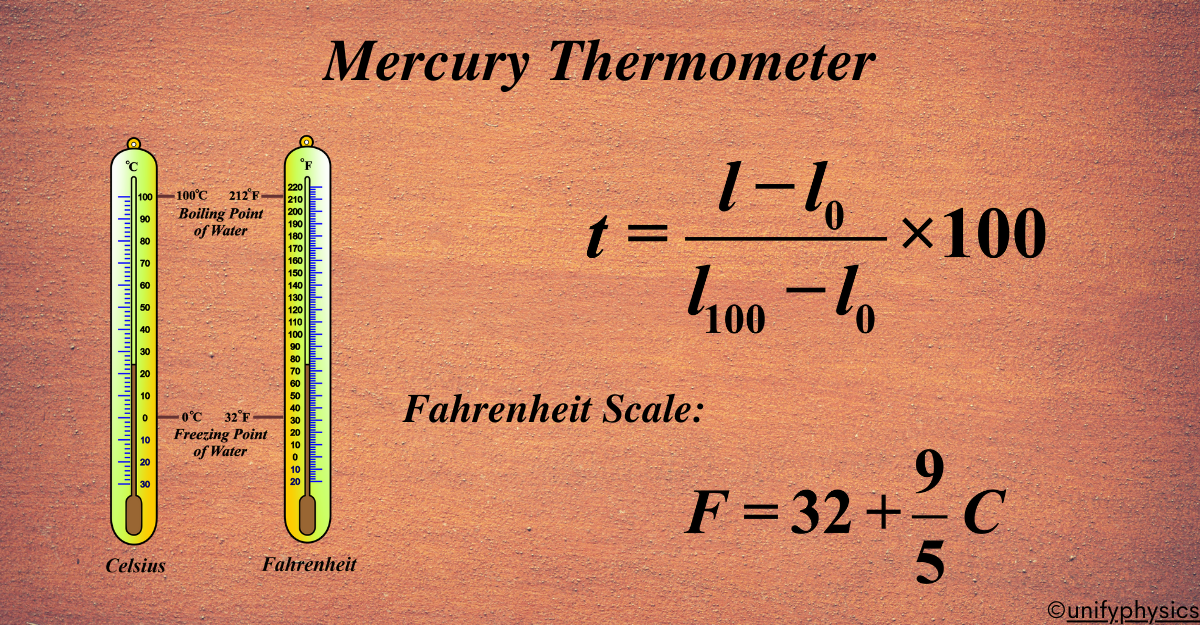
In the Celsius (centigrade) system:
- Ice point = 0°C (t1 = 0)
- Steam point = 100°C (t2 = 100)
Let (l0) = length at 0°C, (l{100}) = length at 100°C.
From above:
\(\displaystyle a = \frac{100}{l_{100} – l_0}\)
b = -a l0
Plug into equation (1):
\(\displaystyle t = \frac{l – l_0}{l_{100} – l_0} \times 100 \tag{2}\)
This is the key expression! Divide the length between (l0) and (l100) into 100 equal parts—each part is 1°C. To measure a body’s temperature:
- Place the bulb in contact with the body.
- Wait for thermal equilibrium (mercury temperature matches the body’s).
- Read the length (l) and use equation (2) to find (t).
Other Scales and Examples
Fahrenheit Scale: Ice point = 32°F, steam point = 212°F. One °F is \(\displaystyle\frac{1}{180}\) of the interval. Normal body temperature is about 98°F. Conversion:
\(\displaystyle F = 32 + \frac{9}{5} C \).
Other Thermometric Properties: Not just mercury! Electric resistance of a metal wire increases with temperature. For a platinum wire: Let ( R0 ) = resistance at 0°C, (R100) at 100°C, (Rt) at temperature (t).
\(\displaystyle t = \frac{R_t – R_0}{R_{100} – R_0} \times 100 \tag{3}\)
This is a platinum resistance thermometer, useful for precise measurements. This method shows that temperature scales are conventions based on measurable changes. In reality, absolute scales like Kelvin exist, but that’s for another lesson.
Also Read: Heat