Before the term ‘electric dipole’ was formally defined, early scientists observed that certain materials could attract or repel each other when rubbed together, indicating the presence of electric charges. This was the foundation upon which the concept of dipoles would be built.
In the 18th century, scientists like Charles-Augustin de Coulomb began quantifying the forces between charges with his famous law. It was understood that charges could exist in pairs with opposite signs, which laid the groundwork for dipoles.
In the late 19th century, German physicist Heinrich Hertz demonstrated the existence of radio waves using a dipole antenna. This practical application of the dipole concept showed how alternating positive and negative charges could emit electromagnetic waves.
The physical chemist Peter J.W. Debye was the first scientist to study molecular dipoles extensively. His work in the early 20th century on the behavior of polar molecules (those with a permanent dipole moment) was groundbreaking. He showed how these dipoles interact with electric fields, which is crucial for understanding phenomena like solvation and chemical reactions.
Today, we understand an electric dipole as a pair of equal and opposite electric charges separated by a distance. This model helps explain a wide range of physical behaviors, from the microscopic interactions between molecules to the design of antennas and the propagation of radio waves.
What is an Electric Dipole?
“An electric dipole consists of two equal and opposite charges separated by a small distance. It’s a system that exhibits a separation of charge.”
An electric dipole is a fundamental concept in the study of electrostatics, which is the branch of physics that deals with the forces exerted by stationary electric charges. Understanding electric dipoles is essential for comprehending various electrical and magnetic phenomena.
An electric dipole is formed when two charges of equal magnitude but opposite nature are separated by a small distance. This pair of charges, often denoted as (+q) and (-q), creates a system that exhibits distinct electrical properties due to the separation of charge.
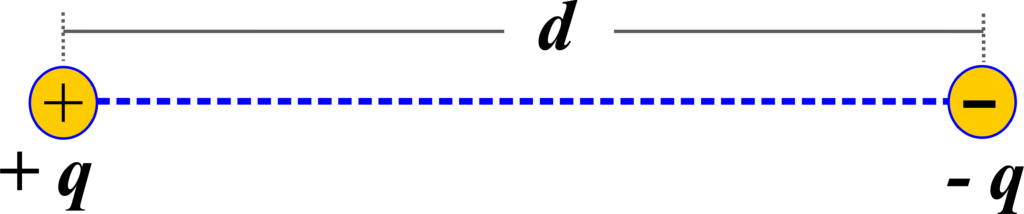
The strength and orientation of an electric dipole are quantified by a vector known as the electric dipole moment, symbolized by ( \(\displaystyle\vec{p}\) ). Mathematically, the electric dipole moment is expressed as the product of the charge (q) and the vector displacement (\(\displaystyle \vec{d}\) ) from the negative to the positive charge, given by the equation:
\(\displaystyle\begin{equation}\label{eqn:1}\boxed{\boldsymbol{\vec{p} = q \vec{d} }} \end{equation}\)
The direction of the electric dipole moment is a critical aspect of its definition. By convention, it is directed from the negative charge to the positive charge. This directional property is significant because it influences how the dipole interacts with external electric fields.
The concept of an electric dipole is not merely a theoretical construct; it has practical implications in various fields. For instance, the behavior of dipoles is key to understanding the electrical properties of molecules in chemistry. In physics, dipoles are used to model the behavior of antennas and to explain the interaction between light and matter.
Magnitude and Dimension of an Electric Dipole
The magnitude of an electric dipole is determined by two factors: the amount of charge and the distance between the charges. It is quantitatively expressed by the electric dipole moment, which is a vector quantity denoted by (\(\displaystyle \vec{p}\)). The electric dipole moment is calculated as the product of the charge (q) and the separation distance (d) between the charges. Mathematically, it is represented as:
\(\displaystyle \vec{p} = q \vec{d} \)
where (q) is the magnitude of one of the charges (positive or negative since they are equal in magnitude) and ( \(\displaystyle\vec{d} \)) is the vector representing the separation between the charges, pointing from the negative to the positive charge.
Dimension of an Electric Dipole: The dimension of an electric dipole moment is a way to express the physical nature of this quantity in terms of the basic physical dimensions. Since the electric dipole moment is the product of charge and distance, its dimension is given by the combination of the dimensions of these two quantities.
In the International System of Units (SI), the dimension of charge is expressed as ( [Q] ), and the dimension of distance is ( [L] ). Therefore, the dimension of the electric dipole moment is:
\(\displaystyle [Q][L] \)
This dimensional expression helps in understanding the nature of the electric dipole moment and in converting between different units of measurement.
In summary, the magnitude of an electric dipole is a measure of its strength and is calculated by multiplying the charge by the distance between the charges. The dimension of an electric dipole provides insight into the types of physical quantities involved in its definition.
What is the Electric Dipole Moment?
The electric dipole moment (\(\displaystyle\vec{p}\)) is a vector quantity that measures the strength and direction of an electric dipole. It’s defined as the product of the charge and the separation vector ( \(\displaystyle\vec{d} \)) pointing from the negative to the positive charge.
The electric dipole moment is a vector quantity that represents the electrical polarity of a system of two charges. It is a measure of the strength and orientation of an electric dipole, providing insight into how the dipole interacts with external electric fields.
To understand the electric dipole moment, consider two point charges of equal magnitude but opposite sign, separated by a distance. The electric dipole moment is defined as the product of the charge and the vector displacement from the negative charge to the positive charge. It is represented by the symbol ( \(\displaystyle\vec{p}\) ) and mathematically given by:
\(\displaystyle \vec{p} = q \vec{d} \)
The direction of the electric dipole moment is crucial because it determines the way the dipole aligns with an electric field. By convention, the electric dipole moment points from the negative charge towards the positive charge. This directional property is not arbitrary; it aligns with the natural tendency of the dipole to orient itself in response to an electric field.
In physics, the electric dipole moment is used to calculate the torque on a dipole in an electric field and to determine the potential energy of the dipole in various configurations. It also helps in understanding the behavior of molecules, as the distribution of electrical charges within them creates a molecular dipole moment that affects their interaction with other molecules and with light.
Direction of Electric Dipole
The direction of the electric dipole moment is from the negative charge to the positive charge. The direction of an electric dipole is a straightforward concept that is crucial for understanding how dipoles behave in an electric field.
In an electric dipole, we have two charges: one positive and one negative. The direction of the electric dipole is defined by the electric dipole moment, which is a vector quantity. This means it has both magnitude and direction. The electric dipole moment points from the negative charge to the positive charge.
In physics, this direction is important because it determines how the dipole interacts with electric fields. When placed in an electric field, the dipole will align itself so that its dipole moment points in the same direction as the electric field. This is the natural orientation that minimizes the potential energy of the dipole in the field.
Potential due to an Electric Dipole
The potential due to an electric dipole is a concept that describes the work needed to move a unit positive charge from a reference point to a specific point within the electric field created by the dipole, without producing any acceleration.
An electric dipole consists of two equal but opposite charges, (+q) and (-q), separated by a distance (d). The electric potential at a point in the field due to a dipole is the sum of the potentials due to each of these charges at that point.
The electric potential (V) at a point due to a dipole can be derived using the principle of superposition, which states that the total potential at a point is the algebraic sum of the potentials due to individual charges. For a dipole, this is given by:
\(\displaystyle V = \frac{1}{4\pi\epsilon_0} \left( \frac{q}{r_+} – \frac{q}{r_-} \right) \)
where (r+) and (r–) are the distances from the positive and negative charges to the point, respectively, and ( \(\displaystyle\epsilon_0 \)) is the permittivity of free space.
If the point where we’re calculating the potential is far away from the dipole, we can make an approximation that (\(\displaystyle r_+ \approx r_- \approx r \)), where (r) is the distance from the dipole’s center to the point. With this approximation, the potential due to the dipole at a point far away is given by:
\(\displaystyle V = \frac{1}{4\pi\epsilon_0} \frac{p \cos\theta}{r^2} \)
Here, (p) is the magnitude of the electric dipole moment (which is (\(\displaystyle q \cdot d )\)), and (θ) is the angle between the dipole axis and the line connecting the dipole’s center to the point.
- The potential due to a dipole decreases with the square of the distance from the dipole (r2), which is different from the electric field that decreases with the cube of the distance (r3).
- When the angle (θ) is 90 degrees, the point is equidistant from both charges, and the electric potential is zero.
- If (θ) is greater than 90 degrees, the potential is negative because the point is closer to the negative charge.
An electric dipole consists of two charges: a positive charge (+q) and a negative charge (-q), separated by a distance (2a). To find the potential at a point P due to this dipole, we’ll consider the contributions from both charges.
The potential at point P due to a single positive charge ( +q ) is given by:
\(\displaystyle V_+ = \frac{kq}{r_+} \)
Similarly, the potential at point P due to a single negative charge (-q) is:
\(\displaystyle V_- = -\frac{kq}{r_-} \)
Here, (r+) and (r–) are the distances from the charges to point P, and ( k ) is Coulomb’s constant. The total potential at point P due to the dipole is the sum of the potentials due to each charge:
\(\displaystyle V = V_+ + V_- \)
\(\displaystyle V = \frac{kq}{r_+} – \frac{kq}{r_-} \)
For an electric dipole, the distance (2a) between the charges is very small compared to the distance (r) from the dipole to point P. This allows us to make the approximation:
\(\displaystyle r_+ \approx r_- \approx r \)
Using the above approximation, we can express (r+) and (r–) in terms of (r) and (a) using the cosine of the angle (θ) between the line joining the charges and the line from the charges to point P:
\(\displaystyle r_+ = r – a\cos\theta \)
\(\displaystyle r_- = r + a\cos\theta \)
Substituting these into the expression for (V), we get:
\(\displaystyle V = \frac{kq}{r – a\cos\theta} – \frac{kq}{r + a\cos\theta} \)
To simplify this, we multiply the numerator and denominator of each fraction by its conjugate:
\(\displaystyle V = \frac{kq(r + a\cos\theta) – kq(r – a\cos\theta)}{(r – a\cos\theta)(r + a\cos\theta)} \)
Simplifying further:
\(\displaystyle V = \frac{2kqa\cos\theta}{r^2 – a^2\cos^2\theta} \)
Since (a) is much smaller than (r), (\(\displaystyle a^2\cos^2\theta \)) is negligible compared to (r2), so we can approximate the denominator as (r2):
\(\displaystyle V = \frac{2kqa\cos\theta}{r^2} \)
The electric dipole moment (p) is defined as (p = 2qa). Substituting this into our expression for (V), we get the final expression for the electric potential due to an electric dipole at point P:
\(\displaystyle\begin{equation}\label{eqn:2}\boxed{\boldsymbol{V = \frac{kp\cos\theta}{r^2} }} \end{equation}\)
Here, (θ) is the angle between the dipole moment and the line from the dipole to point P, (p) is the electric dipole moment, and (r) is the distance from the center of the dipole to point P.
This expression shows that the potential due to an electric dipole decreases with the square of the distance from the dipole and depends on the orientation of the point P relative to the dipole.
Electric Field due to An Electric Dipole
The electric field due to a dipole varies depending on the location:
(i) Electric Field Along the Axial Line:
An electric dipole consists of two charges: a positive charge (+q) and a negative charge (-q), separated by a distance (2a). The axial line is an imaginary line that extends through both charges, starting from the negative charge and going through the positive charge.
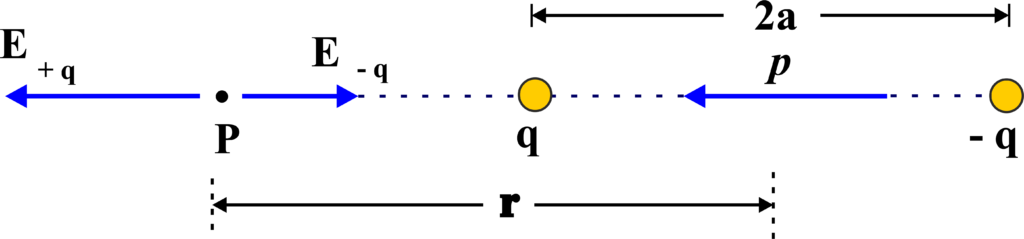
The axial line is the straight line that passes through both the positive and negative charges of the dipole. It’s along this line that we want to calculate the electric field.
The electric field at a point on the axial line is the result of the contributions from both the positive and negative charges. The field due to the positive charge is directed away from the charge, while the field due to the negative charge is directed towards the charge.
To find the net electric field at a point on the axial line, we use the superposition principle. This principle states that the total electric field is the vector sum of the fields due to individual charges.
The electric field (E) at a point on the axial line at a distance (r) from the center of the dipole (and far away from the dipole, such that (\(\displaystyle r \gg a )\)) is given by:
\(\displaystyle E = \frac{1}{4\pi\epsilon_0} \frac{2p}{r^3} \)
Here, (p) is the electric dipole moment, ( \(\displaystyle\epsilon_0 \)) is the permittivity of free space, and (r) is the distance from the center of the dipole to the point on the axial line.
The direction of the electric field along the axial line is the same as the direction of the dipole moment, which is from the negative charge to the positive charge.
- The electric field strength is inversely proportional to the cube of the distance from the center of the dipole (r3).
- The electric field along the axial line is stronger than at equatorial points (perpendicular to the axial line) at the same distance from the dipole.
- The direction of the electric field along the axial line aligns with the dipole moment.
Derivation: The axial line is the imaginary line that extends from the negative charge through the positive charge and beyond.
The electric field at a point P on the axial line, at a distance (r) from the midpoint of the dipole (and far from the dipole, such that (\(\displaystyle r \gg a )\)), due to the positive charge (+q) is:
\(\displaystyle E_+ = \frac{kq}{(r + a)^2} \)
And due to the negative charge (-q) is:
\(\displaystyle E_- = \frac{kq}{(r – a)^2} \)
The net electric field (E) at point P is the vector sum of (E+) and (E–). Since the fields are in opposite directions, we subtract the magnitudes:
\(\displaystyle E = E_+ – E_- \)
\(\displaystyle E = \frac{kq}{(r + a)^2} – \frac{kq}{(r – a)^2} \)
Using the binomial expansion for (\(\displaystyle (r \pm a)^2 \)) and assuming (\(\displaystyle r \gg a \)), we can approximate (\(\displaystyle (r \pm a)^2 \)) as (\(\displaystyle r^2 \pm 2ra \)). Applying this approximation, we get:
\(\displaystyle E = \frac{kq}{r^2 + 2ra} – \frac{kq}{r^2 – 2ra} \)
Combining the terms and simplifying further, we obtain:
\(\displaystyle E = \frac{2kqra}{r^4 – (2ra)^2} \)
Since (\(\displaystyle (2ra)^2 \)) is much smaller than (r4), we can neglect it, leading to:
\(\displaystyle E = \frac{2kqra}{r^4} \)
\(\displaystyle E = \frac{2kqa}{r^3} \)
The electric dipole moment (p) is defined as (\(\displaystyle p = q \cdot 2a \)). Substituting this into our expression for (E), we get the final expression for the electric field due to an electric dipole at point P along the axial line:
\(\displaystyle E = \frac{kp}{r^3} \)
Coulomb’s constant (k) is equal to ( \(\displaystyle\frac{1}{4\pi\epsilon_0} \)),
Substituting (k) gives us the expected result:
\(\displaystyle\begin{equation}\label{eqn:3}\boxed{\boldsymbol{ E = \frac{1}{4\pi\epsilon_0} \frac{2p}{r^3}}} \end{equation}\)
This is the expression for the electric field due to an electric dipole along the axial line. It shows that the electric field is directly proportional to the electric dipole moment and inversely proportional to the cube of the distance from the center of the dipole.
(ii) Electric Field Along the Equatorial Line:
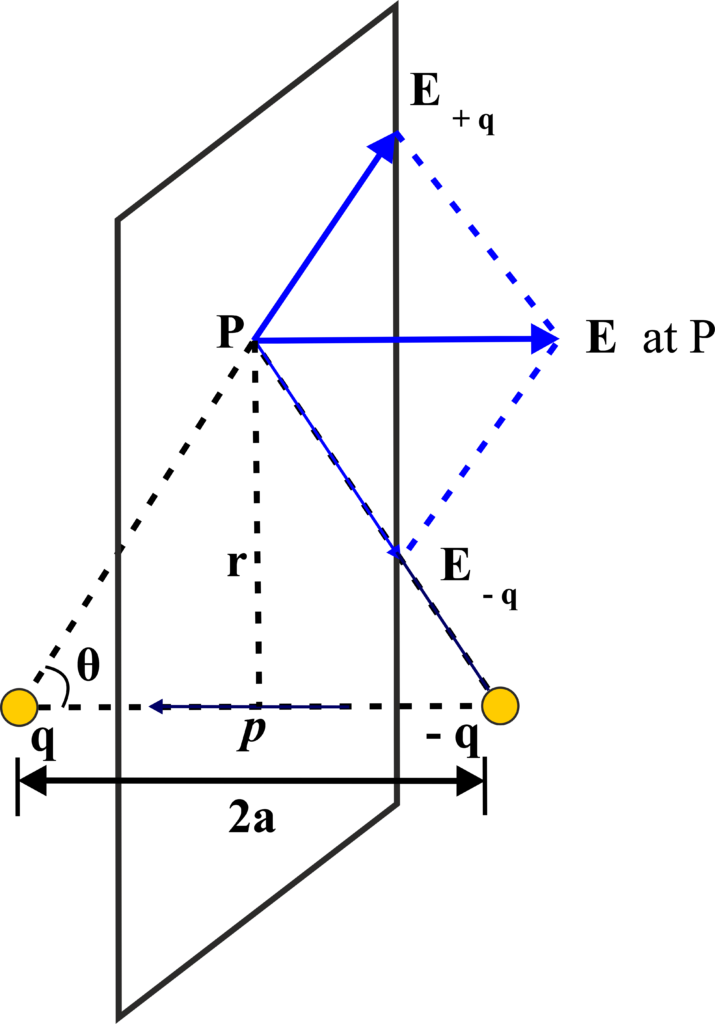
The equatorial line is the line perpendicular to the dipole axis and passes through the midpoint between the two charges. At a point P on the equatorial line, the electric field due to each charge is given by Coulomb’s law. The fields due to the positive and negative charges are equal in magnitude but opposite in direction.
The net electric field at point P is the vector sum of the fields due to the individual charges. Since the fields are opposite in direction, their horizontal components cancel out, and only the vertical components add up.
The vertical component of the electric field due to each charge at point P is:
\(\displaystyle E_{vertical} = E \cos\theta \)
where (θ) is the angle between the line joining the charge to point P and the equatorial line. Using the right triangle formed by the charge, the point P, and the equatorial line, we can express ( \(\displaystyle\cos\theta \)) as:
\(\displaystyle \cos\theta = \frac{a}{\sqrt{r^2 + a^2}} \)
The net electric field at point P is twice the vertical component of one of the fields because the components due to the positive and negative charges are in the same direction:
\(\displaystyle E_{net} = 2E_{vertical} \)
\(\displaystyle E_{net} = 2 \left( \frac{kq}{r^2 + a^2} \right) \left( \frac{a}{\sqrt{r^2 + a^2}} \right) \)
\(\displaystyle E_{net} = \frac{2kqa}{(r^2 + a^2)^{3/2}} \)
The electric dipole moment (p) is defined as
(\(\displaystyle p = q \cdot 2a \)).
Substituting this into our expression for (Enet), we get the final expression for the electric field due to an electric dipole at point P along the equatorial line:
\(\displaystyle E_{net} = \frac{kp}{(r^2 + a^2)^{3/2}} \)
Coulomb’s constant (k) is equal to (\(\displaystyle \frac{1}{4\pi\epsilon_0} \)),
where ( \(\displaystyle\epsilon_0 \)) is the permittivity of free space. Substituting (k) gives us the expected result:
\(\displaystyle\begin{equation}\label{eqn:4}\boxed{\boldsymbol{ E_{net} = \frac{1}{4\pi\epsilon_0} \frac{p}{(r^2 + a^2)^{3/2}}}} \end{equation}\)
This is the expression for the electric field due to an electric dipole along the equatorial line. It shows that the electric field is directly proportional to the electric dipole moment and inversely proportional to the 3/2 power of the sum of the square of the distance from the center of the dipole and the square of half the distance between the charges.
Torque On An Electric Dipole Placed In An Electric Field
Torque on an electric dipole in an electric field is a fundamental concept in physics that describes the rotational effect of the electric field on the dipole.
Torque is a measure of the rotational force applied to an object. It’s the product of the force applied and the distance from the point where the force is applied to the axis of rotation. In the case of an electric dipole, the axis of rotation is the midpoint between the two charges.
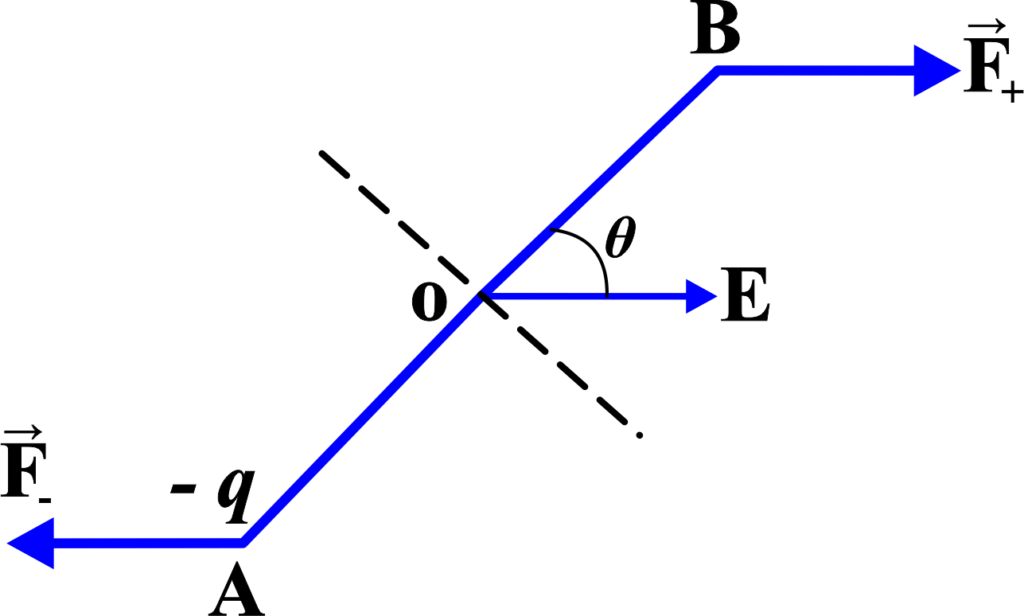
An electric dipole is a pair of equal and opposite charges, (+q) and (-q), separated by a distance (d). The electric dipole moment ( \(\displaystyle\vec{p} \)) is a vector quantity that represents the strength and direction of the dipole, calculated as (\(\displaystyle p = q \times d \)), and points from the negative charge to the positive charge.
When this dipole is placed in a uniform electric field (\(\displaystyle \vec{E} \)), each charge experiences a force due to the field. The force on the positive charge (+q) is ( \(\displaystyle\vec{F}+ = q\vec{E} \)), and the force on the negative charge (-q) is ( \(\displaystyle\vec{F}- = -q\vec{E} \)).
The torque (\(\displaystyle \vec{\tau} \)) on the dipole is given by the cross product of the position vector ( \(\displaystyle\vec{r}\) ) from the pivot point to the point of force application and the force ( \(\displaystyle\vec{F}\) ). For the dipole, the pivot point is the center of the two charges, and the forces are applied at the locations of the charges. The torque due to each force is:
\(\displaystyle \vec{\tau}+ = \vec{r}+ \times \vec{F}+ \)
\(\displaystyle \vec{\tau}- = \vec{r}- \times \vec{F}- \)
Since the forces are equal and opposite, and the position vectors ( \(\displaystyle\vec{r}+ \)) and ( \(\displaystyle\vec{r}- \)) are equal in magnitude but opposite in direction, the torques due to each charge will add up.
The electric dipole moment (\(\displaystyle \vec{p}\) ) is defined as
(\(\displaystyle \vec{p} = q(2\vec{a}) \)),
where (\(\displaystyle \vec{a}\) ) is the vector from the negative charge to the positive charge. The total torque is then:
\(\displaystyle \vec{\tau} = \vec{\tau}+ + \vec{\tau}- \)
\(\displaystyle \vec{\tau} = 2(\vec{a} \times q\vec{E}) \)
\(\displaystyle\begin{equation}\label{eqn:5}\boxed{\boldsymbol{ \vec{\tau} = \vec{p} \times \vec{E}}} \end{equation}\)
The magnitude of the torque is given by:
\(\displaystyle |\vec{\tau}| = |\vec{p}| |\vec{E}| \sin\theta \)
where (θ) is the angle between the electric dipole moment (\(\displaystyle \vec{p}\)) and the electric field (\(\displaystyle\vec{E}\)). The final expression for the torque on an electric dipole in a uniform electric field is:
\(\displaystyle\begin{equation}\label{eqn:6}\boxed{\boldsymbol{|\vec{\tau}| = pE\sin\theta }} \end{equation}\)
This expression shows that the torque is maximum when the dipole is perpendicular to the electric field (θ = 90∘) and zero when the dipole is aligned with the field (θ = 0∘) or (θ = 180∘).
The direction of the torque is given by the right-hand rule. If you point the fingers of your right hand along the direction of (\(\displaystyle \vec{p}\) ) and curl them towards (\(\displaystyle\vec{E}\) ), your thumb will point in the direction of (\(\displaystyle \vec{\tau}\) ). This direction indicates the sense of rotation of the dipole due to the torque.
So, the torque on an electric dipole in an electric field is a vector quantity that depends on the strength of the electric field, the magnitude of the electric dipole moment, and the angle between them.
Potential Energy Of A Dipole Placed In A Uniform Electric Field
An electric dipole consists of two charges of equal magnitude but opposite sign, (+q) and (-q), separated by a distance (2a). When this dipole is placed in a uniform electric field (\(\displaystyle\vec{E}\) ), it experiences a torque, but no net force since the forces on the charges cancel each other out.
To rotate the dipole from an angle (θ0) to (θ) against the electric field, work must be done against the torque. The infinitesimal work (dW) done in rotating the dipole by an infinitesimal angle (dθ) is given by:
\(\displaystyle dW = \tau d\theta \)
where (τ) is the torque experienced by the dipole, which is (pE sinθ) (where (p) is the magnitude of the electric dipole moment). The total work done ( W ) in rotating the dipole from (θ0) to (θ) is the integral of (dW):
\(\displaystyle W = \int_{\theta_0}^{\theta} pE \sin\theta’ d\theta’ \)
\(\displaystyle W = -pE \cos\theta \Big|_{\theta_0}^{\theta} \)
\(\displaystyle W = -pE(\cos\theta – \cos\theta_0) \)
The potential energy (U) of the dipole at an angle (θ) is defined as the negative of the work done by the electric field to bring the dipole from the reference angle (θ0) to (θ). If we choose ( \(\displaystyle\theta_0 = \frac{\pi}{2}\) ) (where the potential energy is zero), the expression for potential energy becomes:
U = -W
\(\displaystyle U = -pE(\cos\theta – \cos\frac{\pi}{2}) \)
\(\displaystyle U = -pE\cos\theta \)
The final expression for the potential energy (U) of an electric dipole in a uniform electric field is:
\(\displaystyle\begin{equation}\label{eqn:7}\boxed{\boldsymbol{U = -pE\cos\theta }} \end{equation}\)
This shows that the potential energy depends on the orientation of the dipole with respect to the electric field and is minimal when the dipole is aligned with the field (θ= 0).
Also Read: Electric Field Lines
Solved Examples
Problem 1: Two charges, (+5 µC) and (-5 µC), are separated by a distance of (2 cm). Calculate the electric dipole moment.
Solution: The electric dipole moment (\(\displaystyle \mathbf{p} \)) is defined as:
\(\displaystyle \mathbf{p} = q \mathbf{d} \)
where (q) is the magnitude of one of the charges and ( \(\displaystyle\mathbf{d} \)) is the separation vector between the charges.
The dipole moment is:
\(\displaystyle p = qd = (5 \times 10^{-6} \, \text{C}) (2 \times 10^{-2} \, \text{m}) \)]
\(\displaystyle p = 10^{-7} \, \text{C} \cdot \text{m} \)
Problem 2: Calculate the electric potential at a point (P) located at a distance (r = 0.1 m) from the center of an electric dipole, along the axial line. The dipole moment is (\(\displaystyle p = 3 \times 10^{-30} \, \text{C} \cdot \text{m} \)).
Solution: The electric potential (V) at a point on the axial line of a dipole is given by:
\(\displaystyle V = \frac{1}{4 \pi \epsilon_0} \frac{p \cos \theta}{r^2} \)
For points on the axial line, (θ = 0∘), so (cos θ = 1 ).
Given: \(\displaystyle\epsilon_0 = 8.85 \times 10^{-12} \, \text{C}^2/\text{N} \cdot \text{m}^2 \)
\(\displaystyle V = \frac{1}{4 \pi \epsilon_0} \frac{p}{r^2} \)
\(\displaystyle V = \frac{1}{4 \pi (8.85 \times 10^{-12})} \frac{3 \times 10^{-30}}{(0.1)^2} \)
\(\displaystyle V = \frac{9 \times 10^9 \cdot 3 \times 10^{-30}}{0.01} \)
\(\displaystyle V = 2.7 \times 10^{-19} \, \text{V} \)
Problem 3: Calculate the electric field at a point on the equatorial line of an electric dipole at a distance (r = 0.05 m) from the center. The dipole moment is (\(\displaystyle p = 2 \times 10^{-29} \, \text{C} \cdot \text{m} \)).
Solution: The electric field (E) at a point on the equatorial line of a dipole is given by:
\(\displaystyle E = \frac{1}{4 \pi \epsilon_0} \frac{p}{r^3} \)
\(\displaystyle E = \frac{1}{4 \pi \epsilon_0} \frac{p}{r^3} \)
\(\displaystyle E = \frac{9 \times 10^9 \cdot 2 \times 10^{-29}}{(0.05)^3} \)
\(\displaystyle E = \frac{18 \times 10^{-20}}{1.25 \times 10^{-4}} \)
\(\displaystyle E = 1.44 \times 10^{5} \, \text{N/C} \)
Problem 4: An electric dipole with dipole moment (\(\displaystyle p = 4 \times 10^{-30} \, \text{C} \cdot \text{m} \)) is placed in a uniform electric field of strength (\(\displaystyle E = 5 \times 10^5 \, \text{N/C} \)) making an angle of (30∘) with the field. Calculate the torque acting on the dipole.
Solution: The torque (τ) on a dipole in a uniform electric field is given by:
\(\displaystyle\tau = pE \sin \theta \)
Given: \(\displaystyle p = 4 \times 10^{-30} \, \text{C} \cdot \text{m} \); \(\displaystyle E = 5 \times 10^5 \, \text{N/C} \); θ = 30∘ ;\(\displaystyle \sin 30^\circ = \frac{1}{2} \)
\(\displaystyle \tau = (4 \times 10^{-30}) (5 \times 10^5) \left(\frac{1}{2}\right) \)
\(\displaystyle \tau = 10^{-24} \, \text{N} \cdot \text{m} \)
Problem 5: Calculate the potential energy of an electric dipole with dipole moment (\(\displaystyle p = 1 \times 10^{-29} \, \text{C} \cdot \text{m} \)) placed in a uniform electric field of (\(\displaystyle 10^4 \, \text{N/C} \)), when the dipole moment is aligned parallel and antiparallel to the field.
Solution: The potential energy (U) of a dipole in a uniform electric field is given by:
\(\displaystyle U = -pE \cos \theta \)
Parallel alignment (θ = 0∘):
\(\displaystyle \cos 0^\circ = 1 \)
\(\displaystyle U_{\text{parallel}} = -pE \cos 0^\circ \)
\(\displaystyle U_{\text{parallel}} = -(1 \times 10^{-29}) (10^4) (1) \)
\(\displaystyle U_{\text{parallel}} = -10^{-25} \, \text{J} \)
Antiparallel alignment (θ = 180∘):
\(\displaystyle \cos 180^\circ = -1 \)
\(\displaystyle U_{\text{antiparallel}} = -pE \cos 180^\circ \)
\(\displaystyle U_{\text{antiparallel}} = -(1 \times 10^{-29}) (10^4) (-1) \)
\(\displaystyle U_{\text{antiparallel}} = 10^{-25} \, \text{J} \)
Problem 6: Two identical dipoles, each with dipole moment (\(\displaystyle p = 2 \times 10^{-30} \, \text{C} \cdot \text{m} \)), are placed at points (A) and (B) separated by a distance (4 cm) along the x-axis. Calculate the net electric field at the midpoint between them.
Solution: Since the dipoles are identical and placed symmetrically, the fields due to each dipole at the midpoint will cancel each other in the y-direction and add up in the x-direction.
The electric field due to each dipole at the midpoint (along the axial line) is:
\(\displaystyle E = \frac{1}{4 \pi \epsilon_0} \frac{2p}{r^3} \)
Since we have two dipoles:
\(\displaystyle E_{\text{net}} = 2E \)
\(\displaystyle E_{\text{net}} = 2 \left( \frac{1}{4 \pi \epsilon_0} \frac{2p}{r^3} \right) \)
\(\displaystyle E_{\text{net}} = \frac{1}{4 \pi \epsilon_0} \frac{4p}{r^3} \)
\(\displaystyle E_{\text{net}} = \frac{9 \times 10^9 \cdot 4 \times 2 \times 10^{-30}}{(0.02)^3} \)
\(\displaystyle E_{\text{net}} = \frac{72 \times 10^{-21}}{8 \times 10^{-6}} \)
\(\displaystyle E_{\text{net}} = 9 \times 10^5 \, \text{N/C} \)
FAQs
What is an electric dipole?
An electric dipole consists of two equal and opposite charges separated by a small distance. It is a simple model used to understand the behavior of electric fields and potentials in the presence of separated charges.
What is meant by the electric dipole moment?
The electric dipole moment is a vector quantity that represents the strength and direction of an electric dipole. It points from the negative charge to the positive charge and its magnitude is the product of the charge and the separation distance between the charges.
How does an electric dipole behave in a uniform electric field?
In a uniform electric field, an electric dipole experiences a torque that tends to align the dipole with the field. The dipole moment vector tends to align parallel to the electric field lines, minimizing the potential energy of the system.
What is the significance of the direction of the electric dipole moment?
The direction of the electric dipole moment vector points from the negative charge to the positive charge. This direction is significant because it indicates how the dipole will align in an external electric field, influencing the dipole’s interaction with the field.
How does the electric potential due to a dipole vary with distance?
The electric potential due to a dipole decreases with the square of the distance from the dipole along the axial line and with the cube of the distance along the equatorial line. This rapid decrease reflects the influence of both charges becoming weaker as the distance increases.
What is the significance of electric dipoles in molecules?
In molecules, electric dipoles are significant because they influence molecular interactions, such as hydrogen bonding and van der Waals forces. These interactions are crucial for determining the physical and chemical properties of substances, including boiling and melting points, solubility, and reactivity.
How can the concept of an electric dipole be applied in real-world situations?
The concept of an electric dipole is applied in various real-world situations, such as understanding the behavior of polar molecules in chemical reactions, the design of antennas in communication systems, and the analysis of electric fields in dielectric materials. Dipole moments also play a role in medical imaging techniques like MRI and in studying the properties of materials in condensed matter physics.