The concept of temperature—how hot or cold something is—has fascinated humans for centuries. Even ancient civilizations noticed the effects of temperature on their surroundings. However, finding precise ways to measure temperature posed a challenge.
Whether ancient Greeks or Chinese had specific ways to measure temperature is unclear. However, we can trace the history of temperature sensors back to the Renaissance. During the Renaissance, scientists and inventors developed methods to measure temperature more accurately.
Robert Hooke (1664), Proposed using the freezing point of water as a reference point for temperature measurement. He suggested that temperatures be measured relative to this freezing point.
Ole Christensen Rømer (Late 17th Century); Recognized the need for two fixed points to create a temperature scale. He chose both Hooke’s freezing point and the boiling point of water as reference points. This allowed interpolation between them.
Gas Laws and Absolute Zero; In the 19th century, scientists studying gas behavior observed that volume changes with temperature. They discovered that gases would theoretically contract to zero volume at an absolute zero temperature. This led to the concept of the Kelvin scale, where absolute zero is the lowest possible temperature.
Santorius’s Thermometer (1612); Santorio Santorini, an Italian physician, invented the sealed liquid thermometer. He observed how liquid moved up a glass tube as it expanded or contracted due to temperature changes. However, this early thermometer lacked precise units.
Daniel Gabriel Fahrenheit (Early 18th Century); Fahrenheit began manufacturing thermometers using alcohol and later mercury. Mercury was ideal due to its linear response to temperature changes over a wide range. Fahrenheit’s scale used fixed points—the freezing and boiling points of water—to create a practical temperature scale.
Bimetallic Temperature Sensors (Late 19th Century); These sensors take advantage of the differential expansion of two bonded metal strips. They are used in thermostats and gas grills, although their accuracy is relatively low.
What is Temperature?
In the realm of physics, understanding the concept of temperature and its relationship with energy is paramount. Whether studying solids, liquids, or gases, the motion of molecules within a substance is intricately linked with energy. This energy, in turn, influences the temperature of an object, which serves as a measure of its hotness or coldness.
Motion and Energy in Matter: At the heart of temperature lies the motion of molecules within a substance. Regardless of the state of matter – solid, liquid, or gas – molecules are in constant motion, each movement associated with a specific form of energy. This energy manifests in various ways, including linear, rotational, and vibrational motion, depending on the state of matter.
Changes in Temperature and Energy
Temperature changes induce alterations in the energy associated with molecular motion. When the temperature of a body increases, so does the overall energy content of its molecules. This increase primarily stems from heightened kinetic energy within the molecules, directly impacting the body’s temperature.
Furthermore, transitions between different states of matter involve shifts in the energy of the constituent atoms and molecules. For instance, during a phase change, such as melting or boiling, there’s a notable change in the potential energy of the molecules, influenced by the intermolecular forces within the substance.
Standard Temperature Scales: Fahrenheit and Celsius
Notably, the Celsius scale is structured with 100 equal intervals between these two reference points, while the Fahrenheit scale encompasses 180 intervals. Temperature scales provide a way to measure temperature and are based on fixed reference points. The three most common scales are:
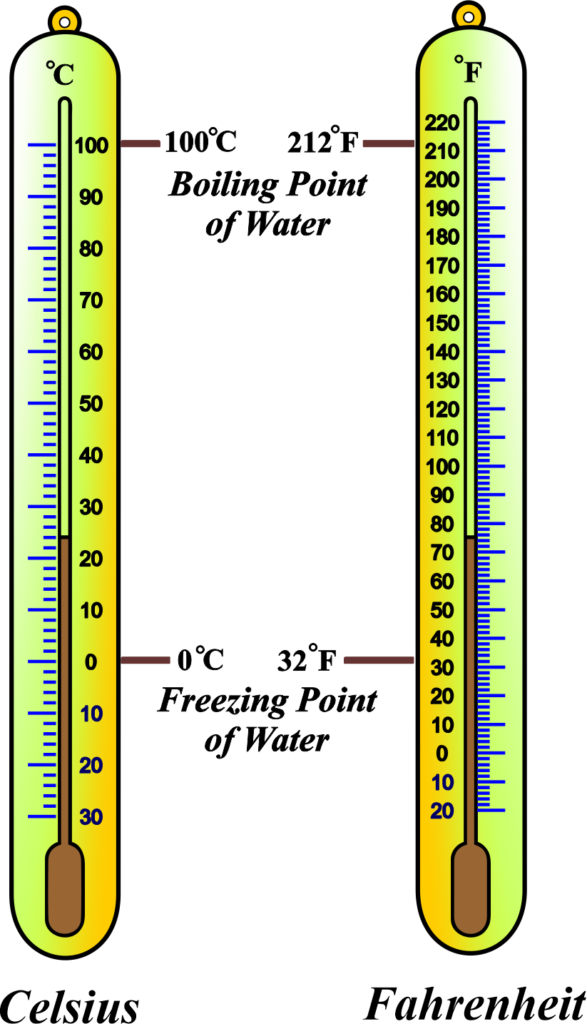
- Celsius (°C): Based on the freezing (0°C) and boiling points (100°C) of water at standard atmospheric pressure.
- Fahrenheit (°F): In this scale, water freezes at 32°F and boils at 212°F.
- Kelvin (K): The Kelvin scale is an absolute temperature scale with its zero point at absolute zero (-273.15°C), the theoretical lowest temperature possible. The freezing point of water is 273.15 K, and the boiling point is 373.15 K.
Converting Between Scales
Converting temperatures between the Fahrenheit and Celsius scales can be achieved through a linear relationship, as represented by the equation:
\(\displaystyle\begin{equation}\label{eqn:1}\boxed{\boldsymbol{\frac{{{{t}_{F}}-32}}{{180}}=\frac{{{{t}_{c}}}}{{100}} }} \end{equation}\)
This equation allows for a straightforward conversion between the two scales, facilitating seamless communication of temperature values across different systems.
This formula is derived from the linear relationship between the Celsius and Fahrenheit scales, where the freezing point of water is 0°C or 32°F, and the boiling point is 100°C or 212°F. The differences in these two fixed points (100°C – 0°C = 100 and 212°F – 32°F = 180) give us the factors for the formula.
To convert from Fahrenheit to Celsius, you can manipulate the formula as follows:
\(\displaystyle t_C = \frac{{5}}{9}(t_F – 32) \)
And to convert from Celsius to Fahrenheit:
\(\displaystyle t_F = \frac{{9}}{5}t_C + 32 \)
Conversion Formulas
To convert temperatures between these scales, you can use the following formulas:
- Celsius to Fahrenheit:
\(\displaystyle F = \frac{9}{5}C + 32 \)
- Fahrenheit to Celsius:
\(\displaystyle C = \frac{5}{9}(F – 32) \)
- Celsius to Kelvin:
\(\displaystyle K = C + 273.15 \)
- Kelvin to Celsius:
\(\displaystyle C = K – 273.15 \)
- Fahrenheit to Kelvin:
\(\displaystyle K = \frac{5}{9}(F – 32) + 273.15 \)
- Kelvin to Fahrenheit:
\(\displaystyle F = \frac{9}{5}(K – 273.15) + 32 \)
These formulas allow you to convert a temperature reading from one scale to another easily.
Measuring Temperature: The Role of Thermometers
The quantification of temperature is made possible through the use of a fundamental device known as a thermometer. Typically filled with either mercury or alcohol, these instruments are calibrated to assign numerical values to specific temperatures. To establish a standardized temperature scale, two fixed reference points are essential. These reference points, correlated with consistent physical phenomena occurring at specific temperatures, serve as the foundation for temperature measurement.
A thermometer is a device that measures temperature or temperature gradient. It consists of two components: a temperature sensor (e.g., the bulb of a mercury-in-glass thermometer) and a means of converting this change into a numerical value (e.g., the scale on the thermometer).
Thermometers work based on the principle of thermal expansion. As the temperature increases, the substance inside the thermometer (usually mercury or colored alcohol) expands and rises in the tube. The scale next to the tube has calibrated marks that correspond to specific temperatures.
Types of Thermometers
- Liquid-in-Glass Thermometers: These contain a liquid that expands and contracts with temperature changes.
- Digital Thermometers: Use electronic sensors to measure temperature and display it on a digital screen.
- Infrared Thermometers: Measure the thermal radiation emitted by an object to determine its temperature.
Thermometers are calibrated according to temperature scales, the most common being Celsius (°C), Fahrenheit (°F), and Kelvin (K). These scales have fixed points, such as the freezing and boiling points of water, which are used to define the scale.
Calibration is the process of setting the scale of the thermometer to known fixed points. For instance, the freezing point of water (0°C or 32°F) and the boiling point of water (100°C or 212°F) at standard atmospheric pressure are often used as calibration marks.
The sensitivity of a thermometer is its ability to detect small temperature changes. Precision refers to how closely multiple measurements will be to each other for the same temperature.
Also Read: Thermal Expansion
Absolute Zero
Absolute zero is the lowest possible temperature where the classical motion of particles that constitute temperature comes to a near halt. This temperature corresponds to the point at which a system’s entropy and enthalpy reach their minimum value, typically taken as zero kelvin (0 K).
- Zero Kelvin: Absolute zero is 0 K on the Kelvin scale, which is equivalent to -273.15°C or -459.67°F.
- Minimal Kinetic Energy: At absolute zero, particles have minimal kinetic energy and vibrational motion due to quantum mechanical effects.
- Theoretical Limit: Reaching absolute zero is a theoretical limit. In practice, scientists can get very close to this temperature but cannot achieve it.
In quantum mechanics, absolute zero is considered the ground state or zero-point energy of a system. Even at absolute zero, particles still possess quantum mechanical energy, which prevents them from being completely motionless. Understanding absolute zero is crucial for studying the behavior of materials at extremely low temperatures, such as superconductivity and Bose-Einstein condensates. It also helps in understanding the laws of thermodynamics, particularly the third law, which states that the entropy of a perfect crystal at absolute zero is exactly zero.
Heat vs. Temperature
| Property | Temperature | Heat |
|---|---|---|
| Definition | Measure of average kinetic energy of molecules within a substance. Indicates hotness or coldness relative to a standard scale. | Transfer of thermal energy between two systems due to a temperature difference. |
| Units of Measurement | Celsius (°C), Fahrenheit (°F), Kelvin (K) | Joules (J), calories (cal) |
| Scale Reference Points | Celsius: 0°C (freezing point of water), 100°C (boiling point of water). Fahrenheit: 32°F (freezing point of water), 212°F (boiling point of water). Kelvin: Absolute zero (0 K). | Not applicable |
| Nature | Influences the physical state of matter, such as melting, freezing, or boiling. | Form of energy, measured in units of joules or calories. |
| Effect on Matter | Does not transfer between systems, and serves as a characteristic property of an object. | Causes changes in internal energy and phase transitions within a system. |
| Transfer Mechanism | Does not transfer between systems, serves as a characteristic property of an object. | Transfers from regions of higher temperature to regions of lower temperature until thermal equilibrium is reached. |
Solve Examples
Example 1: Convert (300 K) to Celsius.
Solution: To convert Kelvin to Celsius, subtract (273.15).
\(\displaystyle 300 \, \text{K} – 273.15 = 26.85°C \)
So, (300 K) is (26.85°C).
Example 2: Calculate the temperature in Celsius and Fahrenheit at absolute zero.
Solution: Absolute zero is (0 K), which is (-273.15°C) in Celsius.
To convert Celsius to Fahrenheit, use the formula
( F = \frac{9}{5}C + 32 ).
\(\displaystyle F = \frac{9}{5}(-273.15) + 32 = -459.67°F \)
So, at absolute zero, the temperature is (-273.15°C) and (-459.67°F).
Example 3: A gas at (-100°C) is heated until its temperature reaches (200°C). Calculate the change in temperature in Kelvin.
Solution: Find the temperature change: (∆T = 200°C – (-100°C) = 300°C ).
To convert Celsius to Kelvin, add ( 273.15 ).
\(\displaystyle \Delta T_{\text{Kelvin}} = \Delta T_{\text{Celsius}} + 273.15 = 300°C + 273.15 = 573.15 \, \text{K} \)
So, the change in temperature in Kelvin is ( 573.15 K).
Example 4: A metal rod cools from (500 K) to (100 K). Calculate the change in temperature in Celsius.
Solution: Find the temperature change:
\(\displaystyle \Delta T = 100 \, \text{K} – 500 \, \text{K} = -400 \, \text{K} \)
Since it’s a decrease in temperature, the change is negative.
So, the change in temperature in Celsius is also (-400 K).
Example 5: If the temperature of a gas is doubled, how does this affect its temperature in Kelvin and Celsius scales?
Solution: Doubling the temperature means multiplying by 2. In the Kelvin scale, doubling the temperature doubles the value.
In the Celsius scale, doubling the temperature also doubles the value, because the Celsius scale is linearly related to the Kelvin scale by ( C = K – 273.15 ).
Example 6: The temperature difference between two objects is ( 50°C ). Express this temperature difference in Kelvin.
Solution: The temperature difference in Celsius is the same as in Kelvin.
So, the temperature difference in Kelvin is also (50 K).
FAQs
Why does metal feel colder than wood at the same temperature?
The metal feels colder because it is a better conductor of heat than wood. When you touch metal, it conducts heat away from your skin faster than wood does, making it feel colder even though both materials might be at the same temperature.
Can two objects at different temperatures have the same thermal energy?
Yes, two objects at different temperatures can have the same thermal energy. Thermal energy depends not only on temperature but also on the mass and specific heat capacity of the object. So, while one object may have a higher temperature if the other has a larger mass or a higher specific heat capacity, it can have the same thermal energy.
Why do we use different temperature scales like Celsius, Fahrenheit, and Kelvin?
Different temperature scales serve different purposes and are based on different reference points. Celsius and Fahrenheit are commonly used for everyday measurements, with Celsius based on the freezing and boiling points of water, while Fahrenheit is based on historical references. Kelvin, on the other hand, is an absolute temperature scale often used in scientific contexts, where 0 K represents absolute zero, the lowest possible temperature.
Why does a balloon deflate when placed in the freezer?
When a balloon is placed in the freezer, the air inside it cools down, causing its volume to decrease. This happens because the kinetic energy of the air molecules decreases as they lose heat to the colder surroundings. As a result, the pressure inside the balloon decreases, leading to deflation.
How does temperature affect the density of substances?
Generally, as the temperature of a substance increases, its density decreases. This is because as the temperature rises, the average kinetic energy of the particles increases, causing them to move faster and spread out more, thereby decreasing the density. Conversely, as temperature decreases, particles slow down and pack more closely together, increasing the density. However, this trend may not hold for all substances, especially those with anomalous behavior like water near its freezing point.
