Electric Flux

The concept of electric flux emerges from the work on electricity and magnetism that began in the 18th century. During this period, scientists were exploring the nature of electric and magnetic fields and trying to understand how they interacted with matter.

The key figure in the history of electric flux is Carl Friedrich Gauss, a German mathematician and physicist. Gauss was a child prodigy and contributed significantly to many fields, including number theory, statistics, analysis, differential geometry, geophysics, electrostatics, astronomy, and optics.

In 1835, Gauss developed a pivotal law in electromagnetism, now known as Gauss’s Law. This law relates the electric flux emerging from a closed surface to the charge enclosed within that surface. However, Gauss’s findings were not immediately published.

It wasn’t until 1867, long after Gauss’s death, that his law concerning electric flux was published. This delay in publication meant that Gauss’s contributions to the field were not fully recognized until later.

Gauss’s Law was revolutionary because it provided a simple way to calculate the electric field in situations with high symmetry. It also formed one of the four Maxwell’s equations, which are the basis of classical electrodynamics.

What is Electric Flux?

Electric flux is a measure of the electric field through a given surface. It quantifies the number of electric field lines passing through that surface and is a scalar quantity, meaning it has magnitude but no direction. The electric flux through a surface is proportional to the total number of electric field lines going through the surface.

Electric flux is a fundamental concept in the field of electromagnetism, particularly in the study of electric fields. It is a measure that quantifies the distribution of the electric field over a given area. To understand electric flux, one must first be familiar with the notion of an electric field, which is a region around a charged particle where a force would be exerted on other charges.

The electric flux through a surface is proportional to the number of electric field lines passing through that surface. It is a scalar quantity, which means it only has magnitude and no direction. The concept of electric flux is crucial because it helps physicists understand and calculate the effect of electric fields in various physical situations, especially when dealing with complex geometries where the electric field varies over space.

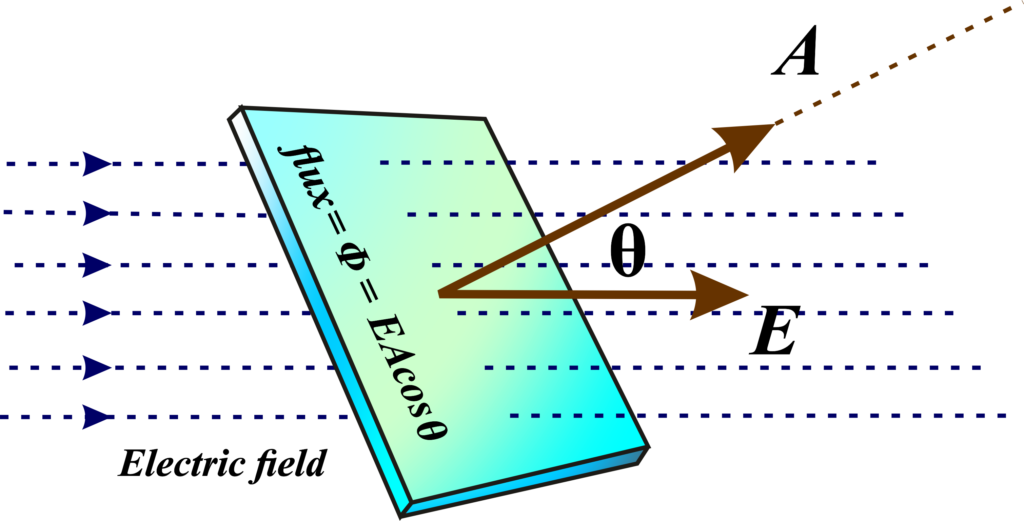
Mathematically, electric flux (Φ) is expressed as the dot product of the electric field (E) and the area vector (A), which is perpendicular to the surface through which the field lines pass. The formula is given by:

\(\displaystyle \Phi = \vec{E} \cdot \vec{A} = E \cdot A \cdot \cos(\theta) \)

Here, (θ) is the angle between the electric field vector and the normal (perpendicular) to the surface. The cosine term accounts for the orientation of the surface relative to the direction of the electric field.

Units of Electric Flux: The unit of electric flux is the newton-meter squared per coulomb (N·m²/C) in the International System of Units (SI). This unit arises naturally from the definition of electric flux, considering that the electric field (E) is measured in newtons per coulomb (N/C) and the area (A) in square meters (m²).

Electric flux is not a flow in the literal sense but rather a measure that allows us to evaluate how an electric field interacts with a given area, which is particularly useful when applying Gauss’s Law to calculate electric fields around charged objects. So, electric flux is a measure of the presence of an electric field over an area, providing insight into the strength and distribution of the field in relation to that area.

Understanding Electric Flux: Electric flux (Φ) is a measure of the electric field (E) passing through a given surface area (A). It’s a way to quantify how much of the electric field interacts with the area.

The electric field (E) is the force per unit charge exerted on a positive test charge placed in the field. It’s represented by the vector (\(\displaystyle \vec{E}\)).

Imagine a flat surface with an area (A) through which the electric field lines are passing. This area is represented by the vector (\(\displaystyle\vec{A}\)), which is perpendicular to the surface.

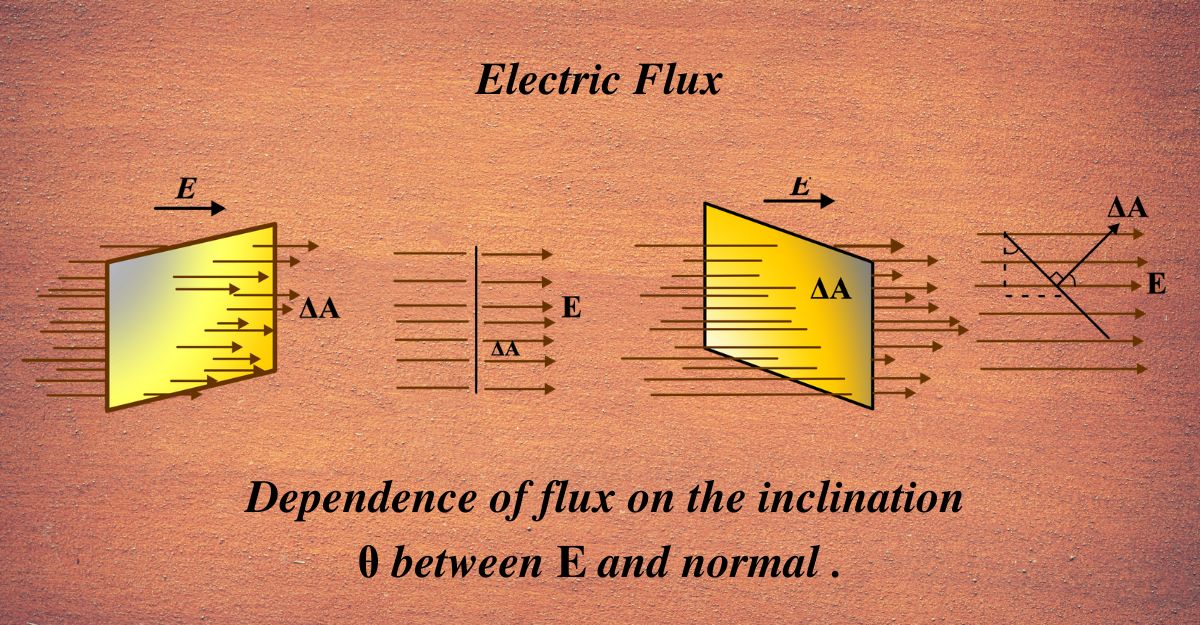
The angle (θ) between the electric field lines and the normal to the surface affects how many field lines pass through the area. If the field is perpendicular to the area, all lines pass through; if parallel, none do.

The electric flux is the dot product of the electric field vector and the area vector. The dot product accounts for both the magnitude of the vectors and the angle between them.

The formula for electric flux (Φ) is:

\(\displaystyle\begin{equation}\label{eqn:1}\boxed{\boldsymbol{ \Phi = \vec{E} \cdot \vec{A} = E \cdot A \cdot \cos(\theta)}} \end{equation}\)

• (Φ) is the electric flux,
• (E) is the magnitude of the electric field,
• (A) is the area through which the field lines pass,
• (θ) is the angle between ( \(\displaystyle\vec{E}\) ) and (\(\displaystyle \vec{A} \)).

For Non-Uniform Fields: If the electric field is not uniform, we consider a small area element (dA) and the corresponding electric field (dE). The total flux is then the integral of (\(\displaystyle dE \cdot dA \)) over the entire surface.

For a uniform electric field and a flat surface, the expression simplifies to:

\(\displaystyle \Phi = E \cdot A \cdot \cos(\theta) \)

For a non-uniform electric field or a curved surface, the expression is:

\(\displaystyle \Phi = \int E \cdot dA \cdot \cos(\theta) \)

where the integral sums up the contributions from all the small area elements over the entire surface. This derivation shows how electric flux is related to the electric field and the geometry of the surface through which the field is passing. It’s a fundamental concept that helps us understand how electric fields interact with physical objects and is widely used in the application of Gauss’s Law in electrostatics.

Factors Affecting Electric Flux

When studying electric flux, it’s important to understand the variables that influence its magnitude. Here are the key factors that affect electric flux:

Electric Field Strength (E): The electric field strength is a measure of the force that a charge would experience at a point in space. The stronger the electric field, the greater the electric flux. This is because a stronger field will have more field lines, and thus, more lines can pass through a given area.

Area of the Surface (A): The area through which the electric field lines pass is directly proportional to the electric flux. A larger area allows more field lines to pass through, increasing the electric flux. Conversely, a smaller area will have fewer field lines passing through it, resulting in a lower electric flux.

Angle (θ) Between the Electric Field and the Normal to the Surface: The angle between the electric field lines and the perpendicular (normal) to the surface is crucial. If the field lines are perpendicular to the surface (θ = 0), the electric flux is maximized because the field lines pass straight through the area. As the angle increases, the effective area through which the field lines pass decreases, reducing the electric flux. At θ = 90 degrees, no field lines pass through the area, and the electric flux is zero.

Permittivity of the Medium (ε): The permittivity of the medium is a measure of how much resistance is encountered when forming an electric field within a medium. Different materials will have different permittivities, which can affect the electric flux. In a medium with high permittivity, the electric field lines are more spread out, which can decrease the electric flux through a given area.

Presence of Charge Within the Surface: For closed surfaces, the electric flux is also affected by the presence of charge within the surface. According to Gauss’s Law, the total electric flux through a closed surface is proportional to the net charge enclosed within that surface.

Electric flux is influenced by the strength and direction of the electric field, the size and orientation of the surface through which the field is measured, the medium’s permittivity, and the charge enclosed by the surface. Understanding these factors is essential for students to grasp how electric flux can vary in different physical situations.

Properties of Electric Flux

Electric flux, denoted by the Greek letter Phi (Φ), is a scalar quantity that plays a significant role in the study of electric fields.

Scalar Quantity: Electric flux is a scalar quantity, which means it has magnitude but no direction. This property simplifies calculations as it does not involve vector analysis.

Magnitude: The magnitude of electric flux represents the total number of electric field lines passing through a given surface. It quantifies the presence of the electric field over the area without considering the direction of the field lines.

Sign Convention: Electric flux can be positive or negative, which is determined by the direction of the electric field lines relative to the surface. If the electric field lines enter a closed surface, the flux is considered negative; if they exit, it’s positive.

Proportional to Electric Field Strength: The electric flux through a surface is directly proportional to the strength of the electric field (E) passing through that surface. A stronger electric field will result in a higher electric flux.

Dependent on Area and Orientation: Electric flux depends on the area of the surface (A) and the angle (θ) between the electric field lines and the normal to the surface. The effective flux is maximized when the field is perpendicular to the surface and decreases as the angle increases.

Independent of the Medium: While the electric field itself can be affected by the medium’s permittivity, the electric flux is independent of the medium. It solely depends on the electric field and the surface’s geometry.

Integral Part of Gauss’s Law: Electric flux is central to Gauss’s Law, which relates the electric flux through a closed surface to the net charge enclosed within that surface. This law is a cornerstone of electrostatics and is used to calculate electric fields in various scenarios.

Electric Flux Through Different Surfaces

When discussing electric flux through different surfaces, it’s essential to distinguish between closed and open surfaces. Here, we’ll first focus on the electric flux through closed surfaces, which is a concept that plays a pivotal role in understanding electric fields and charge distributions.

(i) Flux through Closed Surfaces:

A closed surface is one that completely encloses a volume, like the surface of a balloon or a sphere. It has no edges or openings. The electric flux through a closed surface gives us valuable information about the charge contained within that volume.

The electric flux through a closed surface is calculated by summing up the electric field contributions across the entire surface. Mathematically, it’s represented by the surface integral of the electric field over the closed surface¹.

The key principle that relates electric flux through closed surfaces to the charge enclosed is Gauss’s Law. It states that the total electric flux out of a closed surface is equal to the charge enclosed divided by the permittivity of free space (ε_₀). This can be expressed as:

\(\displaystyle\begin{equation}\label{eqn:2}\boxed{\boldsymbol{\Phi = \frac{Q_{\text{enclosed}}}{\epsilon_0} }} \end{equation}\)

• (Φ) is the electric flux through the closed surface,
• (Q_enclosed) is the total charge enclosed within the surface,
• (ε_₀) is the permittivity of free space.

Gauss’s Law has profound implications. It implies that no matter how large or small the closed surface is, as long as it encloses the same charge, the electric flux will be the same. This means that the electric flux is independent of the shape or size of the closed surface and depends solely on the enclosed charge.

Example: Consider a spherical closed surface surrounding a point charge. The electric field due to a point charge decreases with the square of the distance from the charge. However, the surface area of the sphere increases with the square of the radius. These two effects cancel each other out, resulting in the electric flux through the spherical surface being the same regardless of its radius, as long as it encloses the point charge.

In simple terms, for a closed surface, the electric flux is proportional to the charge enclosed within the surface.

(ii) Flux through Open Surfaces:

When exploring the concept of electric flux, it’s important to understand how it applies to open surfaces. Unlike closed surfaces, which enclose a volume, open surfaces are like a window that allows us to observe the electric field passing through.

An open surface can be visualized as a flat or curved plane that does not completely enclose a space. Examples include the surface of a wall, a sheet of paper, or the side of a box.

The electric flux through an open surface is determined by the electric field strength, the area of the surface, and the orientation of the surface with respect to the electric field lines. The formula for electric flux (Φ) through an open surface is the same as for any surface:

\(\displaystyle \Phi = E \cdot A \cdot \cos(\theta) \)

• (E) is the electric field strength,
• (A) is the area of the surface,
• (θ) is the angle between the electric field lines and the normal to the surface.

The orientation of the open surface in relation to the electric field is crucial. If the surface is perpendicular to the field lines (θ = 0 )), the flux is maximized. As the surface tilts away from the field lines, fewer lines pass through, and the flux decreases. When the surface is parallel to the field lines (θ = 90^∘), no lines pass through, and the flux is zero.

To visualize electric flux through an open surface, imagine counting the number of electric field lines that intersect the surface. The more lines that cross, the greater the flux. This count is a measure of how much electric field is “flowing” through the surface. For an open surface, electric flux depends on the orientation of the surface with respect to the electric field lines.

What is Electric Flux Density?

Electric flux density is a concept in electromagnetism that provides a different perspective on describing electric fields. It is particularly useful when dealing with varying electric fields in different media, such as the boundaries between materials with different electrical properties.

Electric flux density, represented by the symbol (D), is defined as the amount of electric flux passing through a unit area that is perpendicular to the direction of the electric field. It is a vector quantity, which means it has both magnitude and direction. The electric flux density is mathematically expressed as:

\(\displaystyle D = \epsilon E \)

• (D) is the electric flux density,
• (ε) is the permittivity of the medium,
• (E) is the electric field intensity.

The units of electric flux density are coulombs per square meter (C/m²). This unit directly relates to the concept of electric flux density as it quantifies the amount of electric flux in a given area.

Electric flux density is not just a redundant measure given the electric field intensity (E) and the permittivity (ε). While it may seem so in homogeneous media, its importance becomes evident when considering non-homogeneous media or the interfaces between different materials. At such boundaries, the electric flux density helps in understanding how the electric field behaves and changes.

When studying the behavior of electric fields at the boundary between two different media, electric flux density plays a crucial role. It helps in applying the boundary conditions that determine how the electric field lines are refracted or bent at the interface.

Deriving the Expression: To derive the expression for electric flux density, consider a point charge (q) in a uniform medium with permittivity (ε). The electric field intensity at a distance (r) from the charge is given by:

\(\displaystyle E = \frac{1}{4\pi\epsilon} \cdot \frac{q}{r^2} \)

Now, the electric flux (Φ) through a spherical surface of radius (r) centered around the charge is:

\(\displaystyle \Phi = E \cdot 4\pi r^2 \)

Substituting the value of (E) from the above equation, we get:

\(\displaystyle \Phi = \frac{1}{4\pi\epsilon} \cdot \frac{q}{r^2} \cdot 4\pi r^2 \)

Simplifying, we find:

\(\displaystyle \Phi = \frac{q}{\epsilon} \)

Since electric flux density is the flux per unit area, and the area of the spherical surface is (\(\displaystyle 4\pi r^2 \)), we have:

\(\displaystyle D = \frac{\Phi}{4\pi r^2} \)

Substituting the value of (Φ) from the previous step, we get:

\(\displaystyle D = \frac{q}{\epsilon \cdot 4\pi r^2} \)

This equation represents the electric flux density (D) at a distance (r) from a point charge (q) in a medium with permittivity (ε). This equation is derived from the electric field (E) due to a point charge, which is given by:

\(\displaystyle E = \frac{1}{4\pi\epsilon} \cdot \frac{q}{r^2} \)

Now, if we multiply both sides of this equation by (ε), we get:

\(\displaystyle \epsilon E = \frac{\epsilon}{4\pi\epsilon} \cdot \frac{q}{r^2} \)

Simplifying, we have:

\(\displaystyle \epsilon E = \frac{q}{4\pi r^2} \)

This is the expression for electric flux density (D) around a point charge, as we previously derived. So, we can see that:

\(\displaystyle\begin{equation}\label{eqn:3}\boxed{\boldsymbol{ D = \epsilon E}} \end{equation}\)

This equation tells us that the electric flux density is equal to the permittivity of the medium multiplied by the electric field intensity. It’s a general expression that applies not just to the field due to a point charge, but to any electric field in a medium with permittivity (ε). The electric flux density (D) gives us a measure of how much electric field is “concentrated” in a given area and is particularly useful when dealing with different media and boundary conditions in electromagnetism.

The derived expression shows that electric flux density decreases with the square of the distance from the charge and is inversely proportional to the permittivity of the medium.

Electric flux and Gauss’s law

Electric flux and Gauss’s Law are two fundamental concepts in electromagnetism that are closely related. Electric flux, denoted by the Greek letter Phi (Φ), measures the amount of electric field (E) passing through a given area (A). It’s calculated using the formula:

\(\displaystyle \Phi = E \cdot A \cdot \cos(\theta) \)

where (θ) is the angle between the electric field lines and the normal to the surface. The electric flux gives us an idea of how strong the electric field is over a certain area and how it’s oriented with respect to that area.

Gauss’s Law: Gauss’s Law, also known as Gauss’s flux theorem, was formulated by Carl Friedrich Gauss. It relates the electric flux flowing out of a closed surface to the charge (Q) enclosed within that surface. The law is expressed mathematically as:

\(\displaystyle \Phi = \frac{Q}{\epsilon_0} \)

where (ε₀) is the permittivity of free space. This equation tells us that the total electric flux through a closed surface is directly proportional to the net charge enclosed within that surface.

Derivation: Let’s derive the relationship between electric flux and Gauss’s Law using a spherical surface as an example, which is a common Gaussian surface due to its symmetry.

Consider a point charge Q at the center of a sphere with radius r. The electric field due to a point charge is radially outward (or inward if the charge is negative) and has a magnitude given by Coulomb’s law:

\(\displaystyle E = \frac{1}{4\pi\epsilon_0} \cdot \frac{Q}{r^2} \)

Due to the symmetry of the sphere, the electric field at every point on the surface is the same and points radially outward. Thus, the angle θ between the field lines and the normal to the surface is 0 degrees, making (\(\displaystyle\cos(\theta) = 1 \)).

The electric flux through the surface of the sphere is the product of the electric field and the surface area of the sphere:

\(\displaystyle \Phi = E \cdot 4\pi r^2 \)

Replace E with the expression from Coulomb’s law:

\(\displaystyle \Phi = \left( \frac{1}{4\pi\epsilon_0} \cdot \frac{Q}{r^2} \right) \cdot 4\pi r^2 \)

The (r²) terms cancel out, and the (\(\displaystyle 4\pi\)) terms also cancel out, leaving us with:

\(\displaystyle\begin{equation}\label{eqn:4}\boxed{\boldsymbol{\Phi = \frac{Q}{\epsilon_0} }} \end{equation}\)

This is the expression for electric flux according to Gauss’s Law for a point charge within a spherical surface.

The derivation shows that the electric flux through a closed surface is directly proportional to the enclosed charge and inversely proportional to the permittivity of free space. This relationship is fundamental in electrostatics and helps us calculate electric fields for various charge distributions, provided the system has a high degree of symmetry.

Applications of Electric Flux

Electric flux, while a theoretical concept, has practical applications in various fields of physics and engineering.

Gauss’s Law: Electric flux is integral to Gauss’s Law, which is one of Maxwell’s equations. Gauss’s Law relates the electric flux through a closed surface to the charge enclosed within that surface. This principle is fundamental in calculating the electric fields of charge distributions with symmetrical shapes.

Capacitors: In capacitors, electric flux helps us understand how they store energy. The behavior of electric fields between the plates of a capacitor is crucial for determining its capacitance and the amount of charge it can hold.

Electromagnetic Induction: Electric flux is used in the study of electromagnetic induction, which is the process by which a changing magnetic field can induce an electric field. This principle is at the heart of many technologies, such as electric generators and transformers.

Dielectric Materials: The study of dielectric materials, which are insulators that can be polarized by an electric field, also involves electric flux. Understanding how electric flux interacts with these materials is important for designing electronic components like capacitors and insulators.

Electric Field Mapping: Electric flux is used in electric field mapping to visualize and measure the strength and direction of electric fields. This is particularly useful in designing and testing electronic equipment.

Medical Imaging: In medical imaging technologies, such as MRI, electric flux plays a role in the algorithms that process the signals to create images of the body’s interior.

Weather Forecasting: Electric flux measurements are used in weather forecasting to study the behavior of charged particles in the atmosphere, which can affect weather patterns.

Also Read: Electric Field Lines

Solved Examples

Problem 1: A uniform electric field (\(\displaystyle \mathbf{E} = 500 \, \text{N/C}\) ) is directed along the x-axis. Calculate the electric flux through a rectangular plane of area (\(\displaystyle 0.2 \, \text{m}^2 \)) oriented such that its normal vector makes an angle of ( 30^∘) with the x-axis.

Solution: Electric flux (Φ_E) through a surface is given by:

\(\displaystyle \Phi_E = \mathbf{E} \cdot \mathbf{A} = EA \cos \theta \)

Given: \(\displaystyle E = 500 \, \text{N/C} \); A = 0.2 m²; θ= 30^∘

\(\displaystyle \Phi_E = (500) (0.2) \cos 30^\circ \)
\(\displaystyle \Phi_E = 100 \times \frac{\sqrt{3}}{2} \)
\(\displaystyle \Phi_E = 50\sqrt{3} \, \text{N} \cdot \text{m}^2/\text{C} \)

Problem 2: A point charge (q = 5 µC) is placed at the center of a spherical surface of radius (0.1 m). Calculate the electric flux through the surface.

Solution: According to Gauss’s law, the electric flux through a closed surface enclosing a charge is:

\(\displaystyle \Phi_E = \frac{q}{\epsilon_0} \)

\(\displaystyle \Phi_E = \frac{5 \times 10^{-6}}{8.85 \times 10^{-12}} \)
\(\displaystyle\Phi_E = \frac{5}{8.85} \times 10^6 \)
\(\displaystyle\Phi_E = 0.565 \times 10^6 \)
\(\displaystyle \Phi_E = 5.65 \times 10^5 \, \text{N} \cdot \text{m}^2/\text{C} \)

Problem 3: A long straight wire carries a charge density (\(\displaystyle \lambda = 2 \, \mu \text{C/m} \)). Calculate the electric flux through a cylindrical surface of radius (0.1 m) and length (1m) coaxial with the wire.

Solution: Using Gauss’s law for a cylindrical surface:

\(\displaystyle \Phi_E = \frac{q_{\text{enc}}}{\epsilon_0} \)

The charge enclosed by the cylindrical surface:

\(\displaystyle q_{\text{enc}} = \lambda L\)

\(\displaystyle q_{\text{enc}} = (2 \times 10^{-6})(1) = 2 \times 10^{-6} \, \text{C} \)

\(\displaystyle \Phi_E = \frac{2 \times 10^{-6}}{8.85 \times 10^{-12}} \)
\(\displaystyle \Phi_E = \frac{2}{8.85} \times 10^6 \)
\(\displaystyle\Phi_E = 0.226 \times 10^6 \)
\(\displaystyle \Phi_E = 2.26 \times 10^5 \, \text{N} \cdot \text{m}^2/\text{C} \)

Problem 4: Calculate the electric flux density (\(\displaystyle \mathbf{D} \)) at a point where the electric field ( \(\displaystyle\mathbf{E} = 200 \, \text{N/C} \)) in a vacuum.

Solution: Electric flux density ( \(\displaystyle\mathbf{D} \)) is given by:

\(\displaystyle \mathbf{D} = \epsilon_0 \mathbf{E}\)

Given: \(\displaystyle\mathbf{E} = 200 \, \text{N/C} \); \(\displaystyle \epsilon_0 = 8.85 \times 10^{-12} \, \text{C}^2/\text{N} \cdot \text{m}^2 \)

\(\displaystyle \mathbf{D} = (8.85 \times 10^{-12}) (200) \)
\(\displaystyle\mathbf{D} = 1.77 \times 10^{-9} \, \text{C}/\text{m}^2 \)

Problem 5: A point charge (q = 2 µC) is placed at the center of a cube of side (0.2m). Calculate the electric flux through one face of the cube.

Solution: By symmetry, the flux through each face of the cube is the same. The total flux through the cube:

\(\displaystyle\Phi_{\text{total}} = \frac{q}{\epsilon_0} \)

\(\displaystyle \Phi_{\text{total}} = \frac{2 \times 10^{-6}}{8.85 \times 10^{-12}} \)
\(\displaystyle \Phi_{\text{total}} = \frac{2}{8.85} \times 10^6 \)
\(\displaystyle \Phi_{\text{total}} = 0.226 \times 10^6 \)
\(\displaystyle \Phi_{\text{total}} = 2.26 \times 10^5 \, \text{N} \cdot \text{m}^2/\text{C} \)

Since the flux is equally distributed through the six faces of the cube:

\(\displaystyle \Phi_{\text{face}} = \frac{\Phi_{\text{total}}}{6} \)
\(\displaystyle\Phi_{\text{face}} = \frac{2.26 \times 10^5}{6} \)
\(\displaystyle \Phi_{\text{face}} = 3.77 \times 10^4 \, \text{N} \cdot \text{m}^2/\text{C} \)

Problem 6: A spherical surface of radius (0.5 m) encloses a charge of (4 µC). Calculate the electric field just outside the surface using Gauss’s law.

Solution: By Gauss’s law:

\(\displaystyle \oint \mathbf{E} \cdot d\mathbf{A} = \frac{q_{\text{enc}}}{\epsilon_0} \)

For a spherical surface:

\(\displaystyle E \cdot 4 \pi r^2 = \frac{q_{\text{enc}}}{\epsilon_0}\)

Given: r = 0.5 m; \(\displaystyle q_{\text{enc}} = 4 \times 10^{-6} \, \text{C} \); \(\displaystyle\epsilon_0 = 8.85 \times 10^{-12} \, \text{C}^2/\text{N} \cdot \text{m}^2 \)

\(\displaystyle E \cdot 4 \pi (0.5)^2 = \frac{4 \times 10^{-6}}{8.85 \times 10^{-12}} \)
\(\displaystyle E \cdot 4 \pi \cdot 0.25 = \frac{4}{8.85} \times 10^6 \)
\(\displaystyle E \cdot \pi = 0.452 \times 10^6\)
\(\displaystyle E = \frac{0.452 \times 10^6}{\pi} \)
\(\displaystyle E = 1.44 \times 10^5 \, \text{N/C} \)

FAQs