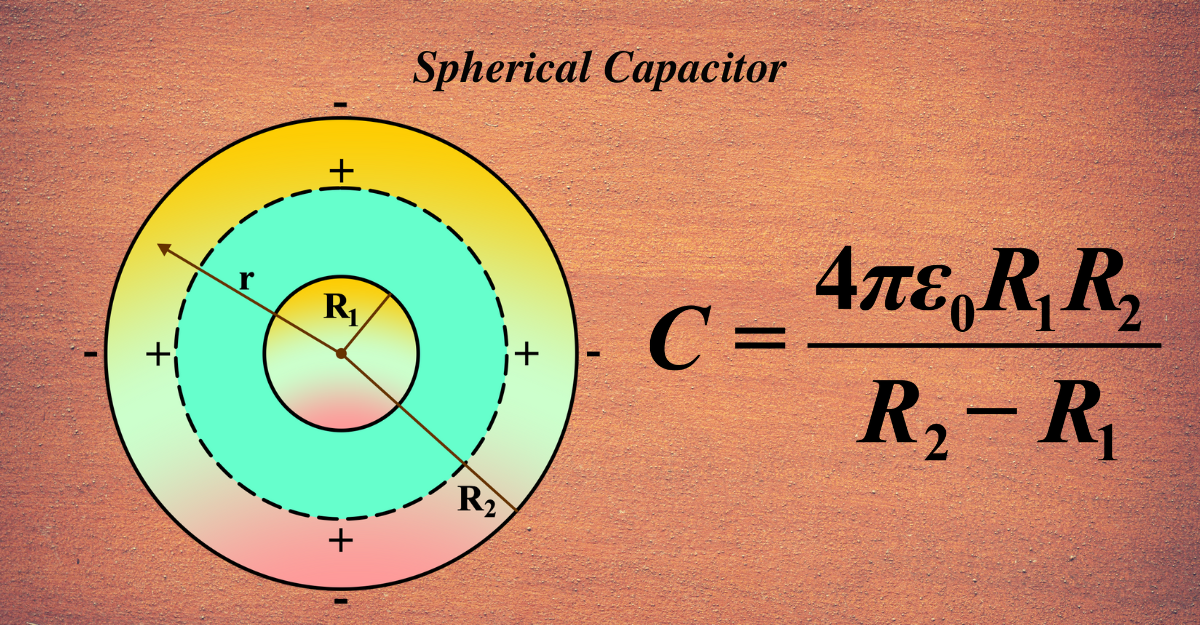Spherical Capacitor

The story of capacitors begins in the 18th century. It was a time of wigs, quills, and the birth of a new kind of electrical device. The earliest capacitors were known as Leyden jars, created around the 1740s. These were simple glass jars filled with water and lined with metal on the inside and outside. They could store a charge, but not very efficiently.

Fast forward to the 19th century, and we meet Michael Faraday, a brilliant scientist with a knack for electricity and magnetism. In the 1830s, Faraday began experimenting with spherical conductors. He imagined two metal spheres, one inside the other, separated by air (which acted as the insulator). By charging these spheres, he could study the electric field and the potential difference between them.

Today, we understand a spherical capacitor as two concentric spherical conductors, separated by a dielectric material. The inner sphere is usually positively charged, while the outer sphere is negatively charged. This creates an electric field in the space between them, which stores energy.

You might wonder, “Why spherical?” Well, spheres are unique because they have symmetry in all directions. This makes the math behind them—like calculating electric fields and potential differences—a bit easier to handle. Plus, they’re a great way to visualize concepts in electrostatics.

While we don’t use spherical capacitors much in everyday electronics, they’ve paved the way for the capacitors we use today. Modern capacitors come in all shapes and sizes, from tiny ones in your smartphone to large ones that help power grids run smoothly.

Definition of Spherical Capacitors

A spherical capacitor consists of two concentric spherical conductors, separated by an insulating material known as a dielectric. The inner sphere is usually positively charged, while the outer sphere is negatively charged, creating an electric field between them.

Imagine you have two shiny, metallic balls, one smaller and one larger. Now, place the smaller ball inside the larger one without touching it. What you now have is a basic model of a spherical capacitor.

The inner ball is called the inner conductor, and the outer ball is the outer conductor. These two are separated by a space that can be filled with air or some other insulating material—this is known as the dielectric.

When you connect these balls to a battery, the inner conductor gets charged positively, and the outer conductor gets charged negatively. This creates an electric field in the space between them, which is where the magic happens—that’s where the energy is stored.

The spherical shape is special because it’s the same in every direction. This symmetry makes it easier to understand and calculate how electric fields and potential differences work in three-dimensional space.

A spherical capacitor is like a storage unit for electric charge. It’s not just about storing charge, though; it’s about understanding the fundamental principles of how electric fields behave around different shapes.

Spherical Capacitors Formula:

Imagine you have two hollow, perfectly round balls, one inside the other. The space between them is what we’re interested in because that’s where the electric field lives. Now, to figure out how good these balls are at storing electric energy, we use a special formula:

\(\displaystyle C = \frac{4\pi\epsilon_0 R_1 R_2}{R_2 – R_1} \)

• C is the capacitance, which tells us how much electric charge the capacitor can hold.
• (\(\displaystyle\pi \)) is our mathematical constant, the ratio of a circle’s circumference to its diameter.
• (\(\displaystyle \epsilon_0 \)) is the permittivity of free space, a measure of how much resistance is encountered when forming an electric field.
• (r₁) is the radius of the inner sphere, the smaller ball.
• (r₂) is the radius of the outer sphere, the bigger ball.

When you see this formula, think of it as a recipe that tells us how to mix the size of our spheres and the nature of space to find out how much electric charge we can store in our spherical capacitor. It’s like finding out how much water you can store in a set of nested bowls—the size of the bowls and the space between them matter a lot.

Structure of Spherical Capacitor

The structure of a spherical capacitor consists of two main components: the inner sphere and the outer sphere, separated by a dielectric material

Inner Sphere (Conductor): The inner sphere of a spherical capacitor is a metallic conductor characterized by its spherical shape, functioning as one of the capacitor’s electrodes.

Outer Sphere (Conductor): The outer sphere in a spherical capacitor is an additional metallic conductor, sharing the same spherical shape as the inner sphere. Functioning as the second electrode of the capacitor, it complements the role of the inner sphere in charge storage and electrical energy transfer.

Positioned concentrically around the inner sphere, the outer sphere forms a symmetrical configuration that optimizes the distribution of electric fields between the two conductors. Similar to the inner sphere, the outer sphere is typically crafted from conductive materials like metal, ensuring efficient conduction and charge accumulation within the capacitor system.

Dielectric Medium: The space between the inner and outer spheres of a spherical capacitor is occupied by a dielectric material, serving a crucial role in the capacitor’s operation.

This dielectric material functions to provide insulation between the two conductors while facilitating the formation of an electric field. It can take various forms, such as air, vacuum, or specific dielectric substances like oil or ceramic.

By offering insulation, the dielectric material ensures the integrity and stability of the capacitor’s structure, allowing efficient charge storage and energy transfer. Additionally, it enables the establishment of an electric field between the spheres, a fundamental aspect of the capacitor’s ability to store electrical energy.

Supporting Structure: The inner and outer spheres of a spherical capacitor typically receive support from non-conductive materials or insulators. By providing stable support, these materials prevent unintended contact between the spheres and help uphold the integrity of the capacitor’s structure.

Insulating materials such as plastic or ceramic are commonly utilized for this purpose due to their excellent electrical insulation properties and mechanical strength.

This ensures reliable support while effectively isolating the conductive spheres from each other, facilitating the proper functioning of the capacitor. Thus, the use of insulating supports is essential for ensuring the stability and performance of spherical capacitors in various applications.

Working Principle

Charge Separation: When a potential difference (voltage) is applied across the spherical capacitor, positive charge accumulates on the outer sphere while negative charge accumulates on the inner sphere. This creates an electric field between the spheres.

Electric Field: The electric field lines emanate radially from the positive charge on the outer sphere towards the negative charge on the inner sphere. The field lines are perpendicular to the surfaces of the spheres and are stronger near the regions of higher charge density.

Capacitance: The capacitance of a spherical capacitor depends on factors such as the radius of the spheres and the separation between them. It is determined by the geometry of the system and can be calculated using mathematical equations.

Energy Storage: The accumulation of opposite charges on the inner and outer spheres creates a potential difference (voltage) between them. This potential difference enables the capacitor to store electrical energy in the form of electrostatic potential energy. The amount of energy stored in the capacitor is directly proportional to the magnitude of the charge and the applied voltage.

Characteristics

• Symmetry: Spherical capacitors exhibit radial symmetry due to their spherical geometry. The electric field lines and charge distribution are radially symmetric around the center of the spheres.
• Uniform Electric Field: In an ideal spherical capacitor, the electric field between the spheres is uniform, assuming the spheres are perfectly spherical and the charge distribution is uniform. However, in practical cases, deviations may occur due to imperfections in the spheres or non-uniform charge distribution.
• High Capacitance: Spherical capacitors can have relatively high capacitance values compared to parallel-plate capacitors with the same surface area. This is because the electric field is concentrated near the surfaces of the spheres, allowing for efficient charge storage.

Spherical Capacitor Derivation

A spherical capacitor is a type of capacitor that consists of two concentric spherical conductors with different radii. The inner conductor has a charge +Q and the outer conductor has a charge -Q. The capacitance of a spherical capacitor depends on the radii of the conductors and the permittivity of the medium between them. The formula for the capacitance of a spherical capacitor is:

\(\displaystyle C = \frac{4 \pi \epsilon_0 R_1 R_2}{R_2 – R_1}\)

First, we need to define a Gaussian surface that encloses the inner sphere and passes through the point of interest between the spheres. A convenient choice is a spherical surface with radius r, where \(\displaystyle R_1 < r < R_2\). The area of this surface is \(\displaystyle 4\pi r^2\).

Imagine you have two hollow, metallic spheres. One is inside the other, and they’re separated by a non-conductive material (like air or plastic). We’ll call the radius of the inner sphere (R₁) and the radius of the outer sphere (R₂).

We give the inner sphere a positive charge ( Q ) and the outer sphere an equal but negative charge (-Q). This sets up an electric field between the two spheres.

To find the electric field (E), we use Gauss’s Law, which tells us that the electric field times the surface area of a sphere is equal to the charge enclosed divided by the permittivity of free space (\(\displaystyle \epsilon_0 \)):

\(\displaystyle E \cdot 4\pi r^2 = \frac{Q}{\epsilon_0} \)

Solving for (E), we get:

\(\displaystyle E = \frac{Q}{4\pi \epsilon_0 r^2} \)

Next, we need to find the potential difference (V) between the two spheres. The potential difference is the work done to move a unit charge from one sphere to the other against the electric field. We calculate it by integrating the electric field over the distance from (R₁) to (R₂):

\(\displaystyle V = \int_{R_1}^{R_2} E \, dr = \int_{R_1}^{R_2} \frac{Q}{4\pi \epsilon_0 r^2} \, dr \)

This gives us:

\(\displaystyle V = \frac{Q}{4\pi \epsilon_0} \left( \frac{1}{R_1} – \frac{1}{R_2} \right) \)

Finally, capacitance (C) is defined as the charge (Q) divided by the potential difference ( V ):

\(\displaystyle C = \frac{Q}{V} \)

Substituting our expression for (V) into the capacitance formula, we get:

\(\displaystyle C = \frac{Q}{\frac{Q}{4\pi \epsilon_0} \left( \frac{1}{R_1} – \frac{1}{R_2} \right)} \)

Simplifying this, we arrive at the capacitance of a spherical capacitor:

\(\displaystyle C = 4\pi \epsilon_0 \frac{R_1 R_2}{R_2 – R_1} \)

What this formula tells us is that the capacitance of a spherical capacitor depends on the sizes of the spheres and the space between them. It’s a measure of how much charge the capacitor can hold for a given potential difference.

Case I: If we assume that the outer sphere is at infinity, we get an isolated single sphere of radius \(\displaystyle R_1\). Then what will be the capacitance? For that, we need to find the potential V of an isolated point charge Q at a distance r from it. We can use the formula:

\(\displaystyle V = \frac{Q}{4\pi\epsilon_0 r}\)

where \(\displaystyle\epsilon_0\) is the permittivity of free space.

To apply this formula to the case of an isolated spherical conductor with radius R and charge Q. The potential V at the surface of the sphere is:

\(\displaystyle V = \frac{Q}{4\pi\epsilon_0 R}\)

To find the capacitance C of the sphere. We can use the definition of capacitance, which states that the ratio of the charge Q to the potential V is constant and equal to the capacitance. Therefore, we have:

\(\displaystyle C = \frac{Q}{V}\)

Substitute the expression for V from the previous step. We get:

\(\displaystyle C = \frac{Q}{\frac{Q}{4\pi\epsilon_0 R}}\)

Simplify this expression by canceling out the Q terms in the numerator and the denominator, and by multiplying both sides by the reciprocal of the fraction in the denominator. We get:

\(\displaystyle C = 4\pi\epsilon_0 R\)

This is the formula for the capacitance of an isolated single sphere.

Case II: If \(\displaystyle R_1 \) and \(\displaystyle R_2\) are made large but $ R_2 – R_1 = d $ is kept fixed, then the above equation for the capacitance of a spherical capacitor will approach the equation for the capacitance of a parallel plate capacitor. This is because the spherical capacitor will become more like two parallel plates with area \(\displaystyle A = 4\pi R_1^2\) and separation d. The formula for the capacitance of a parallel plate capacitor is:

\(\displaystyle C = k \epsilon_0 \frac{A}{d}\)

where k is the relative permittivity or dielectric constant of the material, and \(\displaystyle\epsilon_0\) is the permittivity of free space. Substituting \(\displaystyle A = 4\pi R_1^2\) and d , we get:

\(\displaystyle C = k \epsilon_0 \frac{4\pi R_1^2}{d}\)

This is the equation that the spherical capacitor will approach as \(\displaystyle R_1 \)and \(\displaystyle R_2 \) are made large.

What happens if the inner sphere is earthed?

When the inner sphere of a spherical capacitor is earthed, it means that the inner sphere is connected to the ground, which has a potential of zero.

Any charge that was initially on the inner sphere is neutralized because the earth can supply or absorb an unlimited amount of charge. If a charge (Q) is given to the outer sphere, this charge will distribute itself over the outer surface of the sphere. The inner sphere will have no net charge because it is earthed.

The capacitance of the system changes when the inner sphere is earthed. The formula for the capacitance of a spherical capacitor when the inner sphere is earthed is given by:

\(\displaystyle C = 4\pi\epsilon_0 b \)

where (b) is the radius of the outer sphere and (\(\displaystyle\epsilon_0 \)) is the permittivity of free space.

Conceptually, when the inner sphere is earthed, there are two capacitors formed—one between the outer surface of the outer sphere and the earth, and the other between the inner surface of the outer sphere and the outer surface of the inner sphere. However, since the inner sphere is at zero potential, it effectively becomes part of the earth, and thus, only the capacitance between the outer sphere and the earth is considered.

The energy stored in the capacitor is now only due to the charge on the outer sphere, as the inner sphere cannot store energy because it is at zero potential. By earthing the inner sphere, we simplify the system and change the way it stores charge and energy.

How does this (inner sphere is earthing) affect the electric field between the spheres?

By earthing the inner sphere, we ensure that the electric field between the spheres is solely due to the charge on the outer sphere, and the potential of the inner sphere remains at zero, simplifying the analysis of the electric field in this system.

When the inner sphere of a spherical capacitor is earthed, it affects the electric field between the spheres in the following way: The inner sphere is at zero potential because it’s connected to the earth. Any excess charge it might have had is neutralized.

If a charge (Q) is given to the outer sphere, it will distribute itself over the outer surface. The electric field inside the outer sphere, but outside the inner sphere, is due to this charge (Q).

The electric field (E) at any point between the two spheres is the same as it would be if the charge (Q) were concentrated at the center of the inner sphere. The electric field is given by:

\(\displaystyle E = \frac{Q}{4\pi\epsilon_0 r^2} \)

where (r) is the distance from the center of the inner sphere to the point where the electric field is being measured.

Since the inner sphere is earthed, it does not contribute to the electric field between the spheres. The charge on the inner surface of the outer sphere induces an equal and opposite charge on the outer surface of the inner sphere, which is then neutralized by the earth.

The electric field between the two spheres is uniform and radial, pointing away from the center if the outer sphere is positively charged, or towards the center if the outer sphere is negatively charged.

Energy Stored in a Spherical Capacitor

A spherical capacitor is a space station with two layers: an inner habitat where astronauts live and an outer shell protecting them from space. Now, this space station is special because it can store energy, just like a battery.

When we charge this spherical capacitor, we’re essentially filling it with electric energy. This energy is stored in the electric field that exists between the inner and outer layers of our space station. It’s like pumping air into a balloon—the more air you pump, the more energy you have in the balloon.

The amount of energy (U) stored in this spherical capacitor can be calculated using a simple formula:

\(\displaystyle U = \frac{1}{2} C V^2 \)

Here, (C) is the capacitance of the capacitor (how good it is at storing charge), and (V) is the voltage (the electric pressure pushing the charge).

Think of the energy stored in a capacitor like water in a dam. The water’s potential energy can be released to do work, like turning turbines to generate electricity. Similarly, the energy stored in a capacitor can be released to power things like the flash in a camera or to provide a quick burst of power in electronic devices.

So, when you’re thinking about the energy stored in a spherical capacitor, picture our space station holding onto electric energy, ready to release it when needed. It’s a fantastic way to visualize how capacitors play a crucial role in storing and managing energy in the world of electronics.

Also Read: Capacitor

Application of Spherical Capacitor

• High Voltage Applications: Spherical capacitors are often used in high-voltage applications such as particle accelerators, high-energy physics experiments, and pulsed power systems.
• Laboratory Instruments: They are utilized in laboratory instruments for precision measurements, calibration, and experimental studies involving electric fields and capacitance.
• Research and Development: Spherical capacitors play a crucial role in research and development activities related to electromagnetics, plasma physics, and materials science.
• Radio Frequency Transmitters: These capacitors can also be used in radio frequency transmitters. They’re like the drums in an orchestra, setting the rhythm for the electromagnetic waves that carry music and voices through the air.

Overall, spherical capacitors offer unique advantages in terms of symmetry, electric field distribution, and capacitance, making them valuable components in various technical applications and scientific experiments.

Solved Examples

Problem 1: Calculate the capacitance of a spherical capacitor with an inner radius (r₁ = 0.1 m) and an outer radius (r₂ = 0.2 m).

Solution: The capacitance (C) of a spherical capacitor is given by:

\(\displaystyle C = 4 \pi \epsilon_0 \frac{r_1 r_2}{r_2 – r_1} \)

Given: \(\displaystyle \epsilon_0 = 8.854 \times 10^{-12} \, \text{F/m} \) ; r₁ = 0.1 m$ ; r₂ = 0.2 m$

Calculate (C):

\(\displaystyle C = 4 \pi \times 8.854 \times 10^{-12} \times \frac{0.1 \times 0.2}{0.2 – 0.1} \)
\(\displaystyle C = 4 \pi \times 8.854 \times 10^{-12} \times \frac{0.02}{0.1} \)
\(\displaystyle C = 4 \pi \times 8.854 \times 10^{-12} \times 0.2 \)
\(\displaystyle C = 8.854 \times 10^{-12} \times 0.8 \pi \)
\(\displaystyle C = 7.08432 \times 10^{-12} \, \text{F} \)
\(\displaystyle C \approx 7.08 \, \text{pF} \)

Therefore, the capacitance of the spherical capacitor is (7.08 pF).

Problem 2: A spherical capacitor with an inner radius (r₁ = 0.1 m) and an outer radius (r₂ = 0.3 m) is charged to a potential difference of (V = 100 V) Calculate the energy stored in the capacitor.

Solution: The energy (U) stored in a capacitor is given by:

\(\displaystyle U = \frac{1}{2} CV^2 \)

First, calculate the capacitance (C):

\(\displaystyle C = 4 \pi \epsilon_0 \frac{r_1 r_2}{r_2 – r_1} \)

Given: \(\displaystyle\epsilon_0 = 8.854 \times 10^{-12} \, \text{F/m} \); r₁ = 0.1 m; r₂ = 0.3 m.

Calculate (C):

\(\displaystyle C = 4 \pi \times 8.854 \times 10^{-12} \times \frac{0.1 \times 0.3}{0.3 – 0.1} \)
\(\displaystyle C = 4 \pi \times 8.854 \times 10^{-12} \times \frac{0.03}{0.2} \)
\(\displaystyle C = 4 \pi \times 8.854 \times 10^{-12} \times 0.15 \)
\(\displaystyle C = 5.3148 \times 10^{-12} \pi \)
\(\displaystyle C \approx 16.7 \times 10^{-12} \, \text{F} \)
\(\displaystyle C \approx 16.7 \, \text{pF} \)

Now, calculate the energy stored (U):

\(\displaystyle U = \frac{1}{2} \times 16.7 \times 10^{-12} \times (100)^2 \)
\(\displaystyle U = \frac{1}{2} \times 16.7 \times 10^{-12} \times 10000 \)
\(\displaystyle U = 8.35 \times 10^{-10} \, \text{J} \)
\(\displaystyle U = 0.835 \times 10^{-9} \, \text{J} \)

Therefore, the energy stored in the spherical capacitor is (\(\displaystyle 0.835 \times 10^{-9} \, \text{J} \)) or (0.835 nJ).

Problem 3:A spherical capacitor has an inner radius (r₁ = 0.2 m) and an outer radius (r₂ = 0.4 m). The charge on the capacitor is (\(\displaystyle Q = 5 \times 10^{-9} \, \text{C} \)). Calculate the potential difference across the capacitor.

Solution: The potential difference (V) across a spherical capacitor is given by:

\(\displaystyle V = \frac{Q}{C} \)

First, calculate the capacitance (C):

\(\displaystyle C = 4 \pi \epsilon_0 \frac{r_1 r_2}{r_2 – r_1} \)

Given: \(\displaystyle\epsilon_0 = 8.854 \times 10^{-12} \, \text{F/m}\); r₁ = 0.2 m ; r₂ = 0.4 m; \(\displaystyle Q = 5 \times 10^{-9} \, \text{C} \)

Calculate (C):

\(\displaystyle C = 4 \pi \times 8.854 \times 10^{-12} \times \frac{0.2 \times 0.4}{0.4 – 0.2} \)
\(\displaystyle C = 4 \pi \times 8.854 \times 10^{-12} \times \frac{0.08}{0.2} \)
\(\displaystyle C = 4 \pi \times 8.854 \times 10^{-12} \times 0.4 \)
\(\displaystyle C = 14.167 \times 10^{-12} \, \text{F} \)
\(\displaystyle C \approx 14.167 \, \text{pF} \)

Now, calculate the potential difference (V):

\(\displaystyle V = \frac{5 \times 10^{-9}}{14.167 \times 10^{-12}} \)
\(\displaystyle V = 353 \, \text{V} \)

Therefore, the potential difference across the spherical capacitor is (353 V).

Problem 4:A spherical capacitor with inner radius ( r₁ = 0.05 m ) and outer radius ( r₂ = 0.1 m) is charged to a potential difference of ( V = 200 V) with the inner sphere earthed. Calculate the energy stored in the capacitor.

Solution: The energy (U) stored in a capacitor is given by:

\(\displaystyle U = \frac{1}{2} CV^2 \)

First, calculate the capacitance (C):

\(\displaystyle C = 4 \pi \epsilon_0\frac{r_1 r_2}{r_2 – r_1} \)

Given: \(\displaystyle\epsilon_0 = 8.854 \times 10^{-12} \, \text{F/m} \) ; r_1 = 0.05 m; r_2 = 0.1 m; V = 200 V.

Calculate (C):

\(\displaystyle C = 4 \pi \times 8.854 \times 10^{-12} \times \frac{0.05 \times 0.1}{0.1 – 0.05} \)
\(\displaystyle C = 4 \pi \times 8.854 \times 10^{-12} \times \frac{0.005}{0.05} \)
\(\displaystyle C = 4 \pi \times 8.854 \times 10^{-12} \times 0.1 \)
\(\displaystyle C = 8.854 \times 10^{-12} \times 0.4 \pi \)
\(\displaystyle C = 1.11348 \times 10^{-11} \, \text{F} \)
\(\displaystyle C \approx 11.1 \, \text{pF} \)

Now, calculate the energy stored (U):

\(\displaystyle U = \frac{1}{2} \times 11.1 \times 10^{-12} \times (200)^2 \)
\(\displaystyle U = \frac{1}{2} \times 11.1 \times 10^{-12} \times 40000 \)
\(\displaystyle U = 2.22 \times 10^{-7} \, \text{J} \)
\(\displaystyle U = 222 \times 10^{-9} \, \text{J} \)

Therefore, the energy stored in the spherical capacitor is (\(\displaystyle 222 \times 10^{-9} \, \text{J} \)) or ( 222 nJ).

Problem 5: A spherical capacitor with an inner radius ( r₁ = 0.1 m) and an outer radius ( r₂ = 0.2 m ) is connected to a potential difference of ( V = 50 V ). Calculate the charge on the capacitor.

Solution: The charge (Q) on a capacitor is given by:

\(\displaystyle Q = CV \)

First, calculate the capacitance (C):

\(\displaystyle C = 4 \pi \epsilon_0 \frac{r_1 r_2}{r_2 – r_1} \)

Given: \(\displaystyle\epsilon_0 = 8.854 \times 10^{-12} \, \text{F/m} \) ; r₁ = 0.1 m; r₂ = 0.2 m $ V = 50 V.

Calculate (C):

\(\displaystyle C = 4 \pi \times 8.854 \times 10^{-12} \times \frac{0.1 \times 0.2}{0.2 – 0.1} \)
\(\displaystyle C = 4 \pi \times 8.854 \times 10^{-12} \times \frac{0.02}{0.1} \)
\(\displaystyle C = 4 \pi \times 8.854 \times 10^{-12} \times 0.2 \)
\(\displaystyle C = 8.854 \times 10^{-12} \times 0.8 \pi \)
\(\displaystyle C = 7.08432 \times 10^{-12} \, \text{F} \)
\(\displaystyle C \approx 7.08 \, \text{pF}\)

Now, calculate the charge (Q):

\(\displaystyle Q = 7.08 \times 10^{-12} \times 50 \)
\(\displaystyle Q = 354 \times 10^{-12} \, \text{C} \)
\(\displaystyle Q = 354 \, \text{pC} \)

Therefore, the charge on the spherical capacitor is ( 354 pC).

FAQs