The story of the AC Generator, also known as an alternator, is a fascinating chapter in the history of electricity. It begins with the foundational work of Michael Faraday, who in 1831 discovered electromagnetic induction—the principle that a changing magnetic field within a loop of wire induces an electric current in the wire. This discovery laid the groundwork for all future electric generators.
The development of the AC Generator is tied to several inventors who made significant contributions:
- Hippolyte Pixii (1835): Built the first alternator, which had a rotating magnet and was the precursor to modern generators.
- Sabastian Ziani de Ferranti (1882): Worked on early AC power technology and developed an early transformer.
- Friedrich August Haselwander, C. S. Bradley, and Mikhail Dolivo-Dobrovsky (Late 1880s): Made improvements to the design and efficiency of AC generators.
- Nikola Tesla (1890): Played a crucial role in the development of AC power systems and motors, which were essential for the practical use of AC generators.
The 1880s were a particularly exciting time for the development of electric power. During this decade, the Ganz Company in Budapest began working with single-phase AC power systems, and the Jablochkoff Candle, an early form of street lighting powered by AC generators, was introduced.
The rivalry between AC and DC power came to a head in the “War of Currents,” with Thomas Edison advocating for DC power and George Westinghouse and Nikola Tesla promoting AC power. The ability of AC power to be easily transformed to higher or lower voltages, which allowed for more efficient transmission over long distances, ultimately led to its adoption as the standard for electric power distribution.
By the end of the 19th century, AC generators were being used to power everything from streetlights to factories, setting the stage for the modern electrical grid.
What Is an AC Generator?
An AC Generator, also known as an alternator, is a marvel of engineering that turns mechanical energy into the electrical energy we use every day. Imagine you have a bicycle: when you pedal, you’re creating mechanical energy. Now, what if instead of moving the bike, you could turn those pedals to generate electricity? That’s essentially what an AC Generator does but on a much larger scale.
At its heart, an AC Generator takes mechanical energy—like the kind from a spinning turbine—and converts it into electrical energy in the form of alternating current (AC).
Inside the generator, there’s a coil of wire that spins inside a magnetic field. This spinning, or rotation, is the key. It’s like twirling a magnet near a loop of wire; it generates an electric current in the wire.
This process is based on Faraday’s law of electromagnetic induction. It tells us that a voltage is generated in a coil when it spins in a magnetic field. The faster the spin, the more voltage you get.
The current produced by an AC Generator is called alternating because it changes direction many times a second. This is different from direct current (DC), where the flow of electricity is constant in one direction.
To sum it up, an AC Generator is a device that uses the principles of physics to transform the energy we can make (like turning a turbine) into the energy we can use (electricity to power our homes and gadgets). It’s a critical piece of technology that powers our world!
Construction of AC Generator
An AC Generator, also known as an alternator, is a device that converts mechanical energy into electrical energy.
- Field: The field is made up of coils of conductors that are energized to create a magnetic field. This magnetic field is necessary for the operation of the generator as it interacts with the armature to produce electricity.
- Armature: The armature is the part of the generator where the electrical output is produced. It consists of coils of wire that are large enough to carry the full-load current of the generator. When the armature rotates within the magnetic field, an electromotive force (emf) is induced in these coils.
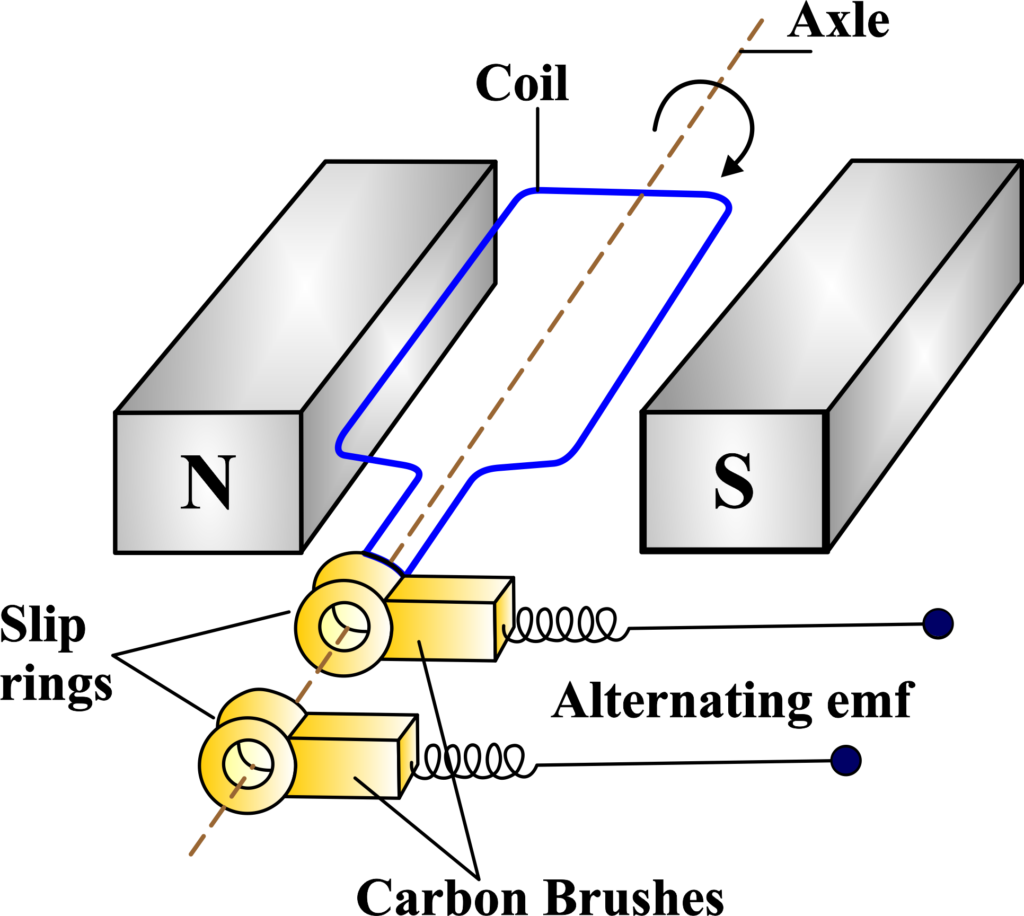
- Prime Mover: The prime mover is the external force that drives the generator. It can be any kind of mechanical energy source, such as a diesel engine, a steam turbine, or a water wheel. The prime mover is responsible for turning the rotor within the stator.
- Rotor: The rotor is the rotating component of the generator. It includes the shaft, and windings, and the electrical output is taken from it. The rotor’s movement within the magnetic field of the stator is what generates the emf.
- Stator: The stator is the stationary part of the generator. It contains the armature winding where the voltage is induced. The stator holds the conductors in place as the rotor turns and plays a crucial role in the generation of electricity.
- Slip Rings: Slip rings are used in AC generators to make an electrical connection between the rotor and the external circuit. They rotate with the rotor and allow the armature to remain stationary, which makes it easier to draw the induced alternating current from the generator.
Each part of the AC Generator plays a vital role in the conversion of mechanical energy to electrical energy.
Slip Rings in an AC Generator
Slip rings are essential for the smooth operation of an AC generator, allowing it to produce and deliver alternating current efficiently. Slip rings provide a continuous electrical connection between the rotating shaft and the stationary components of the generator. This allows the generator to operate without interruption.
Slip rings are made up of two main parts: a metal ring and a carbon brush. The metal ring is typically made of conductive materials like copper, brass, or bronze and is mounted on the generator’s rotating shaft.
As the generator’s rotor (the rotating part) spins, it creates a magnetic field that induces an alternating current in the rotor windings. The slip rings, which are attached to the rotor, rotate with it.
The carbon brushes are stationary and maintain contact with the slip rings. As the slip rings rotate, they transfer the electrical current produced by the rotor to the brushes, which then pass it on to the external circuitry.
Without slip rings, the electrical connections to the rotor would break as it spins. Slip rings ensure a stable and continuous flow of electricity from the rotating rotor to the stationary parts of the generator, enabling the generated electrical energy to be transmitted to the load or power grid.
They are the bridge that connects the moving parts of the generator with the outside world, ensuring that the electricity generated can light up our homes and power our devices.
Working Principle of AC Generator
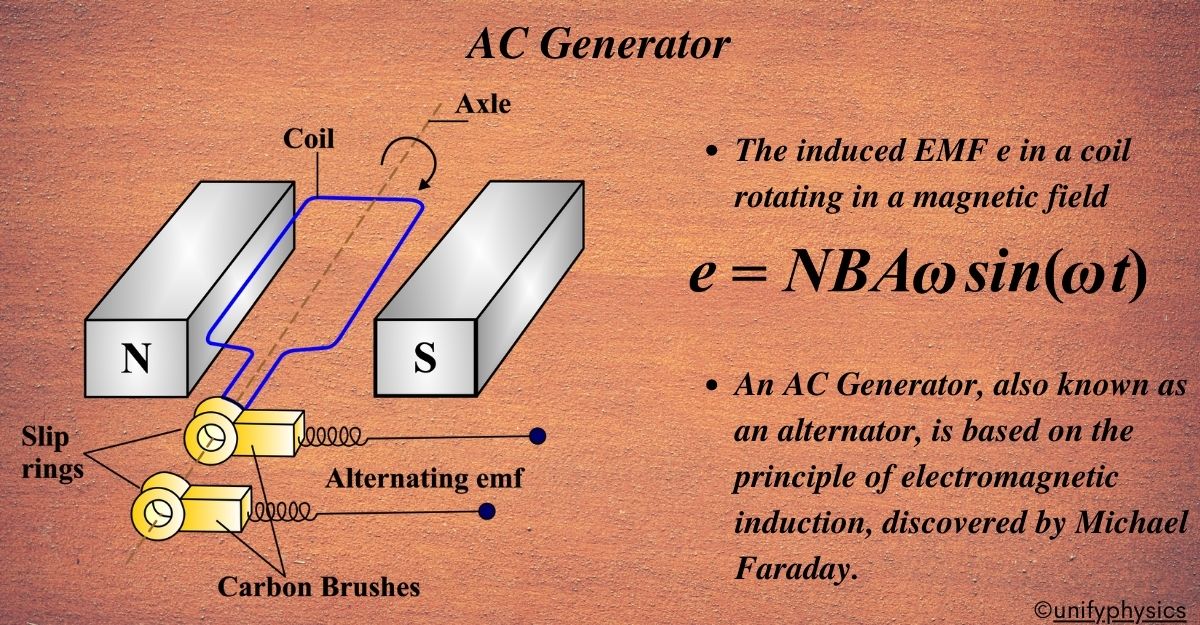
An AC Generator, also known as an alternator, is based on the principle of electromagnetic induction, discovered by Michael Faraday. This principle states that an electromotive force (EMF) is induced in a conductor when it experiences a change in magnetic flux.
Magnetic Field: The generator consists of a magnetic field, which can be provided by permanent magnets or electromagnets. When the armature rotates within the magnetic field, it cuts through the magnetic flux lines, inducing an emf according to Faraday’s law of electromagnetic induction. This emf causes a current to flow in the armature coil.
Rotation: A coil of wire, known as the armature, is placed within this magnetic field. When the armature is rotated, usually by a mechanical force like a turbine (the prime mover), it cuts through the magnetic lines of force.
Induction of EMF: As per Faraday’s law, this movement of the armature within the magnetic field induces an EMF across the ends of the coil. The amount of induced EMF is proportional to the rate of change of the magnetic flux.
AC Generation: As the armature continues to rotate, the direction of the induced current changes periodically, resulting in an alternating current (AC) output. This AC output is then utilized to power electrical devices or is fed into the electrical grid for distribution.
Fleming’s Right-Hand Rule: According to Fleming’s right-hand rule, when the thumb, forefinger, and middle finger of the right hand are held perpendicular to each other, with the forefinger pointing in the direction of the magnetic field (north to south), the thumb pointing in the direction of motion (rotation) of the conductor, the middle finger will point in the direction of the induced current.
Mathematical Expression: The induced EMF e in a coil rotating in a magnetic field can be expressed as:
\(\displaystyle e = NBA \omega \sin(\omega t) \)
- N = Number of turns in the coil
- B = Magnetic field strength
- A = Area of the coil
- ω = Angular velocity of the coil
- t = Time
The sinusoidal nature of the \(\displaystyle \sin(\omega t) \) term in the equation reflects the alternating nature of the current produced by the generator.
Emf Induced in an AC Generator
To understand the induced emf in an AC Generator, imagine a loop of wire spinning in a magnetic field. This is similar to a merry-go-round at a playground, where the changing position of a magnet on the ride would affect a wire loop placed nearby.
Inside the generator, we have a coil with N turns, each with an area A. This coil is placed in a steady magnetic field B. The coil is rotated at v revolutions per second. At time t = 0 s, it starts perpendicular to the magnetic field.
As the coil spins, the magnetic field through it changes, inducing an emf. The formula for this emf is:
\(\displaystyle e = NBA(2\pi v)\sin(2\pi vt) \)
This shows that the emf varies sinusoidally with time, which is the hallmark of alternating current (AC). To find the direction of the induced emf, we use Fleming’s Right-Hand Rule. If the forefinger points in the direction of the magnetic field (B), the thumb in the direction of the coil’s motion, then the middle finger will point in the direction of the induced current.
This law states that the induced emf will oppose the change that created it, maintaining equilibrium in the system. In real-world AC Generators, this induced emf generates the alternating current that powers our homes and devices.
By spinning a coil within a magnetic field, we induce an emf that alternates in direction. This is the fundamental principle behind the AC Generator, which harnesses the laws of physics to bring electricity to our world.
Fleming’s Right-Hand Rule:
“If you hold your right hand with the thumb, forefinger, and middle finger perpendicular to each other, with the thumb representing the direction of motion of the conductor, the forefinger representing the direction of the magnetic field, and the middle finger representing the direction of the induced current, then you have Fleming’s Right-Hand Rule.”
Types of AC Generators
Single-phase Generators:
When we talk about electricity in our homes, we’re usually referring to single-phase AC power. A Single-phase AC Generator is a type of electrical generator that produces this kind of power.
A single-phase generator uses a single, alternating current to produce electrical power. This means the current flows in one direction, then reverses and flows in the opposite direction.
Inside the generator, there’s a rotating part called the rotor and a stationary part called the stator. The rotor spins inside the stator, and as it does, it generates an alternating magnetic field. This field induces an alternating current in the stator’s windings, which is the electricity we use.
The electrical power from a single-phase generator can be represented as a sine wave. This wave fluctuates from a positive peak to a negative peak. Imagine a wave in the ocean rising and falling—that’s similar to how the current in a single-phase generator behaves.
Because it only uses one wave of power, a single-phase generator’s output isn’t as consistent as a three-phase generator’s. It reaches a peak of power, then dips down, which can make it less efficient for large, industrial applications.
Single-phase generators are typically used in homes and small businesses where the power demands aren’t as high as in large industrial settings. They’re perfect for powering everyday appliances like your fridge, TV, and lights.
In essence, single-phase AC generators are the unsung heroes in our homes, quietly and efficiently providing the power we need for our daily lives. They might not be as powerful as their three-phase cousins, but they’re just right for keeping our gadgets and appliances running smoothly.
Three-phase Generators:
Three-phase AC Generators are the powerhouses behind our modern electrical grid. They’re like the big brothers of single-phase generators.
Unlike single-phase generators that produce one alternating current, three-phase generators produce three separate currents. These three currents are generated simultaneously, and each one is offset by 120 degrees from the others in terms of the phase.
Inside a three-phase generator, there are three coils placed 120 degrees apart. As the rotor spins, it induces an alternating current in each coil. Because of the physical separation and the timing of the rotation, the three currents peak at different times.
If you look at the electrical output on a graph, you’ll see three sine waves, each representing one of the phases. They rise and fall just like ocean waves, but each one is staggered, so when one is at its peak, the others are not.
This setup provides a more consistent flow of power. With three overlapping waves, there’s always one reaching a peak, which means the power delivery is smoother and more stable. This is great for running motors and other heavy machinery that need a constant supply of power.
Three-phase power is more efficient for transmitting electricity over long distances, which is why it’s used for the electrical grid. It can also power large motors and heavy loads with less electrical loss.
You’ll find three-phase generators in industrial settings, large commercial buildings, and in the power plants that send electricity to our homes. They’re the workhorses that keep the lights on and machines running in the most demanding situations.
So, Three-phase AC Generators are essential for industries and our modern way of life, providing reliable and efficient power where it’s needed most. They ensure that our factories run smoothly, our offices stay lit, and our homes remain comfortable.
Frequency of an AC Generator
The frequency of an AC Generator refers to how many times the current changes direction per second. It’s like the heartbeat of the generator, dictating the rhythm at which the electrical current oscillates.
The frequency is determined by how fast the generator’s coil or magnetic field rotates. If you have a coil spinning inside a magnetic field, each full turn (360 degrees) represents one complete cycle of alternating current.
The formula to calculate the frequency (f) of an AC Generator is:
\(\displaystyle f = \frac{P \times N}{60} \)
where (P) is the number of poles in the generator and (N) is the speed of the rotor in revolutions per minute (RPM). The number 60 converts RPM to seconds, as frequency is measured in cycles per second, or Hertz (Hz).
In most residential power systems, the standard frequency is either 50 Hz or 60 Hz. This means the current changes direction 50 or 60 times each second. The frequency needs to be stable because many of our appliances are designed to operate at a specific frequency. If the frequency is too high or too low, it can cause them to malfunction or get damaged.
In three-phase generators, each phase produces its own AC waveform. The three waveforms are evenly spaced, creating a continuous and balanced power supply. The frequency of each phase is the same, ensuring a consistent delivery of power.
Difference Between AC and DC Generator
| Feature | AC Generator | DC Generator |
|---|---|---|
| Definition | Converts mechanical energy into AC electrical power. | Converts mechanical energy into DC electrical power. |
| Current Direction | Electrical current reverses direction periodically. | Electrical current flows only in one direction. |
| Design | Coil is fixed, magnet moves. Simpler construction. | Coil rotates in a fixed field. Complex due to commutators. |
| Commutators | Does not have commutators. | Has commutators to direct current flow. |
| Rings | Has slip rings. | Does not have slip rings. |
| Efficiency of Brushes | Brushes do not wear quickly, more efficient. | Brushes and commutators wear out, less efficient. |
| Short Circuit Risk | Lower risk due to efficient brushes. | Higher risk due to wear and sparking. |
| Rotating Parts | Rotor has low current, high resistivity. | Rotor is generally heavy. |
| Current Induction | Output can be induced in stator or rotor. | Output can only be induced in the rotor. |
| Output Voltage | Produces high voltage, varies in amplitude and time. | Produces steady voltage. |
Advantages of AC Generators
Efficient Long-Distance Transmission: AC Generators are capable of transmitting electricity over long distances with minimal energy loss. This is because AC voltage can be easily increased or decreased using transformers, which reduces the current and, as a result, the energy lost as heat due to resistance in the wires.
Simplicity in Design: The design of AC Generators is relatively simple, especially when compared to DC Generators. This simplicity translates to lower manufacturing costs and easier maintenance.
Compatibility with AC Motors: Most household and industrial motors are designed to run on AC power. AC Generators produce the type of current that these motors need, making them highly compatible with a wide range of applications.
Use of Transformers: AC power can be transformed to higher or lower voltages very efficiently, which is essential for the practical distribution of electricity. High voltages are used for transmission to reduce losses, and then the voltage is lowered for safe residential or commercial use.
Safety: The ability to transform AC voltage means that high voltages, which are more dangerous, can be used where necessary (like for power transmission) and then reduced to safer levels for consumer use.
Three-Phase Power: AC Generators can produce three-phase power, which is more efficient for both transmission and for running large motors in industrial settings.
Reliability: AC Generators are generally more reliable and have a longer lifespan than DC Generators, partly because they have fewer components that can wear out, such as commutators.
Flexibility in Power Generation: AC Generators can be scaled up or down in size to generate different amounts of power, making them versatile for various needs, from powering a single home to an entire city.
Disadvantages of AC Generator
- Complexity in Handling: AC Generators can be more complex to handle due to the high voltages they operate with. This requires careful design and operation to ensure safety.
- Need for Additional Insulation: Because AC Generators deal with large currents and high voltages, they require additional insulation to prevent accidents and ensure the longevity of the generator’s components.
- Less Durable Compared to DC Generators: Generally, AC Generators are not as durable as DC Generators. The components of AC Generators, particularly those involved in voltage transformation and current induction, can be more susceptible to wear and tear over time.
- High Voltage Risks: Working with AC Generators involves dealing with high voltages, which can be dangerous. Extra precautions must be taken to manage these risks, especially during maintenance and repair work.
- Cost of Transformers: While transformers allow for efficient voltage transformation, they also add to the cost and complexity of the electrical system. Each step-up or step-down in voltage requires a transformer, which can be expensive.
- Synchronization Issues: In systems where multiple AC Generators are used, synchronization is crucial. If generators are not perfectly synchronized, it can lead to power quality issues and even damage the electrical grid.
- Frequency Variation: The frequency of the AC current must be carefully controlled. Variations in frequency can cause problems with sensitive equipment and can be challenging to manage.
Uses of AC Generator
AC Generators, also known as alternators, are used in a variety of applications due to their ability to produce alternating current (AC). Here are some common uses:
Electricity Generation: AC Generators are primarily used in power plants to generate electricity. They are driven by steam turbines, gas turbines, or combustion engines to convert mechanical energy into electrical energy.
Transportation: They are used in vehicles such as electric scooters and hybrid electric vehicles (HEVs) to provide electrical power for the drive systems.
Household Appliances: Many household appliances, like microwaves, use AC Generators to convert mechanical energy into the electricity needed for operation.
Marine Applications: Sailboats often use AC Generators to power onboard equipment and systems when away from shore power sources.
Remote Power Supply: In areas without access to the electrical grid, portable AC Generators are used to supply power for tools, lights, and other equipment.
Emergency Power: AC Generators are essential for providing backup power during outages, ensuring that critical systems like hospitals and data centers remain operational.
Renewable Energy Systems: They are also used in renewable energy setups, such as wind turbines, where they convert the mechanical energy from wind into electrical energy.
These are just a few examples of how AC Generators are used in our daily lives. Their versatility and efficiency make them an indispensable part of modern electrical systems.
Also Read: AC Voltage Applied to a Resistor
Examples
Example 1: In an AC generator, if the number of turns in the coil is doubled and the area of the coil is halved, the maximum emf induced in the coil will be.
Solution: In an AC generator, the maximum emf \(\displaystyle\varepsilon \) induced in the coil is given by the formula:
\(\displaystyle\varepsilon = NBAω \)
According to the problem, the number of turns N is doubled and the area A is halved. We need to find out how these changes affect the maximum emf.
Initially, let’s denote the original maximum emf as \(\displaystyle\varepsilon_1 \). After the changes, let’s denote the new maximum emf as \(\displaystyle\varepsilon_2 \).
Given that the number of turns is doubled and the area is halved, the new values become:
N’ = 2N
A’ = \(\displaystyle\frac{A}{2} \)
Now, substituting these values into the formula for maximum emf, we get:
\(\displaystyle\varepsilon_2 = N’BA’ω \)
\(\displaystyle = (2N) \cdot \left( \frac{A}{2} \right) Bω \)
\(\displaystyle = NBAω\)
This is the same as the original maximum emf \(\displaystyle \varepsilon_1 \). Hence, doubling the number of turns and halving the area of the coil does not change the maximum emf induced in the coil.
Example 2: An AC generator has an output voltage of 120V when the frequency of the rotation is 60 Hz. What will be the output voltage if the frequency is increased to 90 Hz?
Solution: The output voltage of an AC generator is given by the formula:
\(\displaystyle\varepsilon = NBAω \)
We know that \(\displaystyle \varepsilon \) is directly proportional to ω . This means that if ω increases, \(\displaystyle \varepsilon \) also increases proportionally.
Given that the frequency f is increased from 60 Hz to 90 Hz, we can find the ratio of the new voltage \(\displaystyle\varepsilon_2 \) to the original voltage \(\displaystyle\varepsilon_1 \):
\(\displaystyle\frac{\varepsilon_2}{\varepsilon_1} = \frac{f_2}{f_1} \)
\(\displaystyle = \frac{90 \, \text{Hz}}{60 \, \text{Hz}} \)
\(\displaystyle = \frac{3}{2} \)
So, the new voltage \(\displaystyle\varepsilon_2 \) will be \(\displaystyle \frac{3}{2} \) times the original voltage \(\displaystyle\varepsilon_1 \):
\(\displaystyle \varepsilon_2 = \frac{3}{2} \times 120 \, \text{V} \)
\(\displaystyle = 180 \, \text{V} \)
Therefore, if the frequency is increased to 90 Hz, the output voltage of the AC generator will be 180 V.
Example 3: A coil of 100 turns and an area of 0.01 m2 rotates in a magnetic field of 0.1 T with an angular speed of 100 rad/s. The maximum emf induced in the coil is:
Solution: The formula for maximum emf \(\displaystyle\varepsilon\) induced in the coil is:
\(\displaystyle \varepsilon = NBAω \)
Substituting the given values, we get:
\(\displaystyle \varepsilon = 100 \times 0.01 \times 0.1 \times 100 \)
\(\displaystyle = 10 \, \text{V} \)
The maximum emf induced in the coil is 10 V.
Example 4: A coil having 200 turns and an area of 0.02 m2 rotates in a magnetic field of 0.1T with an angular speed of 100 rad/s. What will be the maximum emf induced in the coil if the number of turns is increased to 400 and the area is decreased to 0.02 m2?
Solution: Initially, we have the following parameters:
The formula for maximum emf \(\displaystyle\varepsilon \) induced in the coil is:
\(\displaystyle\varepsilon = NBAω\)
Substituting the given values, we get the original maximum emf \(\displaystyle\varepsilon_1 \):
\(\displaystyle\varepsilon_1 = 200 \times 0.02 \times 0.1 \times 100 \)
\(\displaystyle = 40 \, \text{V} \)
After the changes, we have:
- Number of turns, N2 = 400
- Area of the coil, A2 = 0.02 m2
The new maximum emf \(\displaystyle\varepsilon_2 \) becomes:
\(\displaystyle\varepsilon_2 = 400 \times 0.01 \times 0.1 \times 100 \)
\(\displaystyle = 40 \, \text{V} \)
Therefore, the maximum emf induced in the coil remains 40 V after doubling the number of turns and halving the area.
Example 5: An AC generator has a coil with 200 turns and an area of 0.02 m2 rotating at an angular frequency of 100 rad/s in a magnetic field of 0.1 T. Calculate the maximum emf induced in the coil.
Given parameters: The formula for maximum emf \(\displaystyle\varepsilon \) induced in the coil is:
\(\displaystyle\varepsilon = NBAω \)
Substituting the given values, we get:
\(\displaystyle \varepsilon = 200 \times 0.02 \times 0.1 \times 100 \)
\(\displaystyle = 40 \, \text{V} \)
The maximum emf induced in the coil is 40 V, which matches the previous solution.
FAQs
What is an AC generator?
An AC generator, also known as an alternator, is a device that converts mechanical energy into electrical energy by producing alternating current (AC). It operates on the principle of electromagnetic induction.
How does an AC generator work?
An AC generator works by rotating a coil within a magnetic field, or by rotating a magnetic field around a stationary coil. The rotation changes the magnetic flux through the coil, inducing an alternating voltage and current in the coil due to Faraday’s law of electromagnetic induction.
What are the main components of an AC generator?
The main components of an AC generator include the rotor (the rotating part), the stator (the stationary part), slip rings (to provide a connection to the rotating coil), brushes (to transfer the current from the slip rings to an external circuit), and a prime mover (such as an engine or turbine to provide mechanical energy).
What is the role of the slip rings and brushes in an AC generator?
Slip rings and brushes in an AC generator provide a continuous connection between the rotating coil and the external circuit. The slip rings are connected to the ends of the coil and rotate with it, while the brushes are stationary and maintain contact with the slip rings to transfer the generated AC to the external circuit.
What is the difference between an AC generator and a DC generator?
The primary difference between an AC generator and a DC generator is the type of current they produce. An AC generator produces alternating current (AC), where the direction of the current periodically reverses. A DC generator produces direct current (DC), where the current flows in one direction. This difference is achieved through the use of slip rings in AC generators and commutators in DC generators.
How is the frequency of the generated AC determined in an AC generator?
The frequency of the generated AC in an AC generator is determined by the speed at which the rotor turns and the number of poles in the generator. It is calculated by the formula (f = (N \times P) / 120), where (f) is the frequency in hertz, (N) is the rotational speed in revolutions per minute (RPM), and (P) is the number of poles.
What are some common applications of AC generators?
AC generators are widely used in various applications, including power stations to generate electricity for homes and industries, in vehicles to charge batteries and power electrical systems, in portable generators for emergency power supply, and in renewable energy systems like wind turbines to convert mechanical energy into electrical energy.