The story of the LCR circuit begins with the fundamental understanding of electricity and magnetism. In the 19th century, scientists like Michael Faraday and James Clerk Maxwell laid the groundwork with their pioneering work on electromagnetic fields. Their discoveries showed that electric and magnetic fields could store energy, which is a principle that underpins the operation of LCR circuits.
The combination of three components (Inductor, Capacitor, Resistor) into a single circuit was a natural progression as scientists and engineers sought to control and manipulate electrical signals. The LCR circuit became a cornerstone of electronic design, allowing for the precise control of electrical oscillations and the filtering of signals.
The LCR circuit found its first major application in the field of radio. In the early 20th century, as radio technology was developing, the ability to select specific frequencies from the airwaves became crucial. The LCR circuit, with its resonant properties, was perfect for this task. It allowed radios to tune into specific stations by resonating at particular frequencies.
Today, LCR circuits are everywhere. They’re in the filters that shape the sound in your headphones, the oscillators that keep time in your watch, and the tuners that select channels on your TV. They’re an essential part of the infrastructure that makes modern electronics work.
What is an LCR Circuit?
An LCR circuit is like a team of three unique players, each with a special role, working together in an electrical game. Imagine electricity as a ball being passed around in this game. The three players are:
L (Inductor): This player is like a goalkeeper who can catch and hold the ball (electricity) for a while, storing it as a magnetic field. When the time is right, the goalkeeper releases the ball back into the game.
C (Capacitor): This player is like a springboard on the field. When the ball hits it, the springboard stores some energy and then bounces the ball back with extra energy, storing and releasing the electrical energy in an electric field.
R (Resistor): This player controls the pace of the game, making sure the ball doesn’t move too fast or too slow. It’s like a coach who sets the speed of the drills, dissipating energy as heat to manage the flow of current.
In a series LCR circuit, these three players are lined up one after another. The ball (current) has to go through each player every time it makes a round of the field. This means the current is the same through all components.
The real magic happens when these players work together at a certain rhythm, called the resonant frequency. At this frequency, the inductor and capacitor pass the ball back and forth so perfectly that they seem to disappear, leaving only the resistor to control the game. This is when the circuit can control signals most effectively, like tuning into your favorite radio station with crystal clear sound.
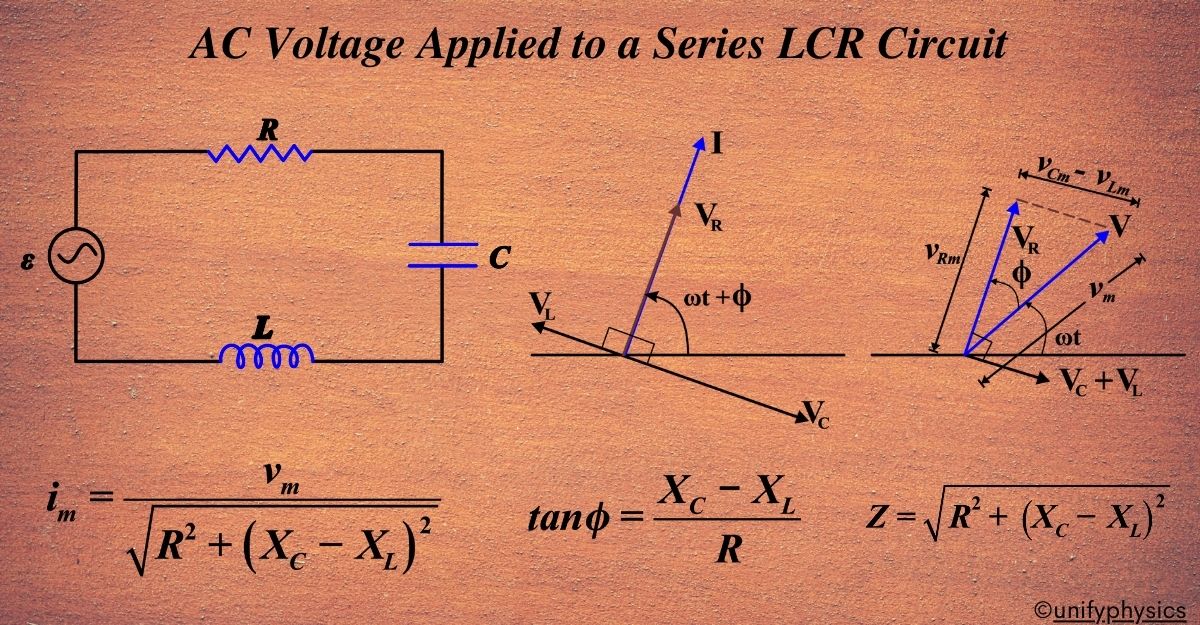
AC Voltage Applied to a Series LCR Circuit
When AC voltage is applied to a series LCR circuit, the voltage source alternates, causing the current to change direction periodically. This current interacts with each component in the circuit—resistor, inductor, and capacitor —in unique ways due to their distinct properties:
- Resistor: It offers resistance to the flow of current, which is constant and independent of the frequency of the applied voltage. The voltage across the resistor VR is in phase with the current I.
- Inductor (L): It has inductive reactance XL that increases with the frequency of the applied voltage. The voltage across the inductor VL leads the current by 90 degrees because the inductor resists changes in current by generating a magnetic field.
- Capacitor: It has capacitive reactance XC that decreases with the frequency of the applied voltage. The voltage across the capacitor VC lags behind the current by 90 degrees as the capacitor stores and releases energy in its electric field.
In a series LCR circuit connected to an AC source (let’s call it \(\displaystyle \varepsilon \)), we can describe the voltage of the source using a sine function:
\(\displaystyle v = v_m \sin(\omega t)\)

If ‘q’ represents the charge on the capacitor and ‘i’ represents the current at a given time ‘t’, according to Kirchhoff’s loop rule, we have an equation that describes the relationship between the voltage, current, and other circuit elements.
\(\displaystyle L\frac{{di}}{{dt}}+iR+\frac{q}{C}=v\)
We’re trying to find out two things: the current at any given moment (instantaneous current) and how it relates to the voltage from the power source (applied alternating voltage). To solve this problem, we’ll use two different methods:
- Phasors: This method involves using simplified representations of voltage and current called phasors to understand their relationship.
- Analytical Solution: In the second method, we’ll solve the equation \(\displaystyle v = v_m \sin(\omega t)\) to figure out how the current changes over time.
Phasor-diagram solution
In the circuit we’re looking at, the resistor, inductor, and capacitor are connected in a row (series). Because of this setup, the alternating current (AC) flowing through each of these components is the same at any given time. They all have the same strength (amplitude) and are in sync with each other. We can represent this current with the equation
\(\displaystyle i = i_m \sin(\omega t + \varphi) \),
where \(\displaystyle \varphi \) represents the phase difference between the voltage from the power source and the current in the circuit.
We have a phasor called ( I ) representing the current in the circuit, given by the equation \(\displaystyle i = i_m \sin(\omega t + \varphi) \).
Now, let’s talk about the voltages across different parts of the circuit:
- V represents the voltage from the power source.
- VR represents the voltage across the resistor, and it’s aligned in the same direction as ‘I’.
- VC represents the voltage across the capacitor, and it lags ‘I’ by \(\displaystyle \pi/2 \) (90 degrees).
- VL represents the voltage across the inductor, and it leads ‘I’ by \(\displaystyle \pi/2 \) (90 degrees).
In the diagram, these voltages are shown with the appropriate relationships to ( I ) in terms of phase.
Phasors and Amplitudes: In this context, we’re using phasors to represent the current and voltages in the circuit. The length of these phasors, or how long they are, corresponds to the amplitude of the voltages across the resistor VR, capacitor VC, and inductor VL. These amplitudes are calculated using the following formulas:
- \(\displaystyle V_{Rm} = i_m \cdot R\)
- \(\displaystyle V_{Cm} = i_m \cdot X_C \)
- \(\displaystyle V_{Lm} = i_m \cdot X_L \)
Voltage Equation for the Circuit: We have an equation \(\displaystyle L\frac{{di}}{{dt}}+iR+\frac{q}{C}=v\) that describes how the voltages across the inductor, resistor, and capacitor add up to the voltage from the source can be written as,
\(\displaystyle v_L + v_R + v_C = v\)

Phasor Relationship: We represent this equation using phasors. We draw phasors for VL, VR, and VC with appropriate angles and lengths. Because VC and VL are always in opposite directions, we can combine them into a single phasor (VC + VL). This phasor’s length represents the difference between their amplitudes. Then, using the Pythagorean theorem with V as the hypotenuse and VR and VC + VL as the other sides of a right triangle, we get:
\(\displaystyle v^2 = v_{Rm}^2 + (v_{Cm} – v_{Lm})^2 \)
We can substitute the calculated values of vRm, vCm, and vLm from earlier into this equation to solve for V. After substitution, we get the equation
\(\displaystyle v^2 = i_m^2 R^2 + (i_mX_C – i_mX_L)^2 \)
\(\displaystyle v^2 = i_m^2 \left[ R^2 + (X_C – X_L)^2 \right]\)
This simplifies to
\(\displaystyle\boldsymbol{ i_m = \frac{v_m}{\sqrt{R^2 + (X_C – X_L)^2}}}\)
Impedance: Similar to resistance in a circuit, we introduce a new concept called impedance Z in an AC circuit. The equation represents it,
\(\displaystyle\boldsymbol{ Z = \sqrt{R^2 + (X_C – X_L)^2} }\).
In simple terms, we’re finding the relationship between voltage ‘V’ and current ‘i’ in the circuit. We use impedance ‘Z’ to represent the total opposition to the flow of current in the circuit, just like resistance. It’s calculated using the square root of the sum of the squares of resistance and the difference between reactances XC ) and XL .
Phase Angle ( Φ ): Since phasor ‘I’ is always parallel to phasor VR, we look at the angle between VR and V to find the phase angle Φ. Using the formula
\(\displaystyle \tan \phi = \frac{{v_{Cm} – v_{Lm}}}{{v_{Rm}}} \)
and substituting values from the equations \(\displaystyle v_{Rm} = I_m \cdot R \), \(\displaystyle v_{Cm} = I_m \cdot X_C \), and \(\displaystyle v_{Lm} = i_m \cdot X_L \), we get
\(\displaystyle\boldsymbol{ \tan \phi = \frac{{X_C – X_L}}{R}} \).
When ( XC > XL ), the circuit is capacitive, and the current leads the voltage. The phase angle (Φ) is positive, indicating a leading current.
- When \(\displaystyle X_C > X_L \), the circuit is capacitive, and the current leads the voltage. The phase angle (Φ) is positive, indicating a leading current.
- When \(\displaystyle X_L > X_C \), the circuit is inductive, and the current lags the voltage. The phase angle (Φ) is negative, indicating a lagging current.
- When \(\displaystyle X_C = X_L \), the circuit is at resonance, and the current is in phase with the voltage Φ= 0 .
Analytical solution
Let’s start with the differential equation given by the circuit’s voltage equation:
\(\displaystyle L\frac{di}{dt} + iR + \frac{q}{C} = v_m \sin(\omega t) \)
Here, L is the inductance, R is the resistance, C is the capacitance, i is the current, q is the charge on the capacitor, vm is the maximum voltage, and ω is the angular frequency.
We are also given the assumed solution for the charge q on the capacitor:
\(\displaystyle q = q_m \sin(\omega t + \theta) \)
To find the current ‘i’, we differentiate q with respect to time ( t ):
\(\displaystyle i = \frac{dq}{dt} = \omega q_m \cos(\omega t + \theta) \)
and
\(\displaystyle \frac{{{{d}^{2}}q}}{{d{{t}^{2}}}}=-{{q}_{m}}{{\omega }^{2}}\sin \left( {\omega t+\theta } \right)\)
Substituting these values in Eq. \(\displaystyle L\frac{di}{dt} + iR + \frac{q}{C} = v_m \sin(\omega t) \), we get
\(\displaystyle q_m \omega \left[ R\cos(\omega t + \theta) + (X_C – X_L)\sin(\omega t + \theta) \right] = v_m \sin \omega t\)
Multiplying and dividing above Eq.by \(\displaystyle Z = \sqrt{R^2 + (X_C – X_L)^2} \), we have
\(\displaystyle q_m \omega Z \left[ \frac{R}{Z}\cos(\omega t + \theta) + \frac{(X_C – X_L)}{Z}\sin(\omega t + \theta) \right] = v_m \sin \omega t\)
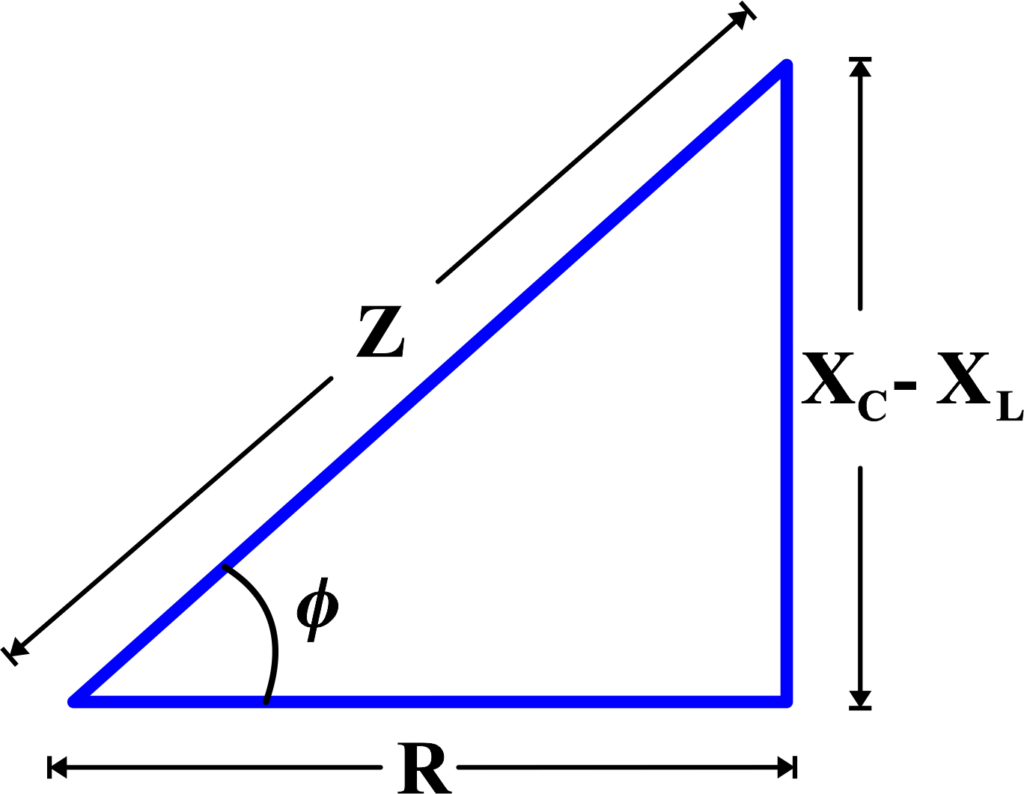
Now , \(\displaystyle \cos \phi =\frac{R}{Z}\)
and \(\displaystyle \sin \phi = \frac{X_C – X_L}{Z}\)
So that, \(\phi = \tan^{-1}\left(\frac{X_C – X_L}{R}\right)\)
Substituting this in the above Eq. and simplifying, we get:
\(\displaystyle q_m \omega Z \cos(\omega t + \theta – \phi) = v_m \sin \omega t\)
Comparing the two sides of this equation, we see that
\(\displaystyle v_m = q_m \omega Z = i_m Z\)
we need to understand that (qm ω) is actually the maximum current (im), because when the charge (q) reaches its maximum value (qm), the rate of change of charge (which is the current) will also be at its maximum and \(\displaystyle \theta =-\frac{\pi }{2}+\phi \)
Substituting ( im ) back into the equation \(\displaystyle i = \frac{dq}{dt} = \omega q_m \cos(\omega t + \theta) \) we get:
\(\displaystyle i = i_m \cos(\omega t + \theta) \)
or, \(\displaystyle\boldsymbol{ i = i_m \sin(\omega t + \phi) }\)
This is the desired equation for the current in a series LCR circuit when an AC voltage is applied, showing the current as a sinusoidal function with amplitude (im) and phase (Φ).
The phase (Φ) indicates how much the current waveform is shifted in time compared to the voltage waveform. This phase shift is due to the reactive components (inductor and capacitor) in the circuit. The amplitude (im) represents the peak value of the current, which is directly proportional to the peak charge (qm) and the angular frequency (ω).
Resonant Frequency of a Series LCR Circuit
The resonant frequency is the frequency at which the circuit naturally oscillates with the maximum amplitude. For a series LCR circuit, this occurs when the inductive reactance (XL) and capacitive reactance (XC) are equal.
Imagine you’re on a swing, and you want to go as high as possible. You pump your legs back and forth at just the right times to make the swing go higher with each push. This is like resonance: you’re adding energy at the perfect moments to maximize your swing’s motion.
The resonant frequency is like that perfect rhythm you find on the swing. It’s the special frequency where the inductor and capacitor pass energy back and forth so smoothly that they seem to cancel each other out. At this point, the circuit swings with the maximum energy—meaning the current flowing through it is at its peak.
To find this perfect rhythm, we use a formula that tells us the resonant frequency (f0) of the circuit:
\(\displaystyle f_0 = \frac{1}{2\pi\sqrt{LC}} \)
Here, (L) is the inductance, and (C) is the capacitance. The (\(\displaystyle 2\pi \)) is like the full cycle of the swing, back and forth.
As we know in a series LCR circuit, we have two types of reactance:
- Inductive Reactance (XL): This is how the inductor reacts to changing current. It’s given by the formula (\(\displaystyle X_L = 2\pi fL \)), where (f) is the frequency and (L) is the inductance.
- Capacitive Reactance (XC): This is how the capacitor reacts. It’s given by (\(\displaystyle X_C = \frac{1}{2\pi fC} \)), where (C) is the capacitance.
At resonance, the inductive and capacitive reactances are equal but opposite in phase, so they cancel each other out. This means:
\(\displaystyle X_L = X_C \)
\(\displaystyle 2\pi fL = \frac{1}{2\pi fC} \)
To find the resonant frequency (f0), we rearrange the equation:
\(\displaystyle f^2 = \frac{1}{(2\pi)^2LC} \)
Taking the square root of both sides gives us:
\(\displaystyle f = \frac{1}{2\pi\sqrt{LC}} \)
So, the expression for the resonant frequency (f0) of a series LCR circuit is:
\(\displaystyle f_0 = \frac{1}{2\pi\sqrt{LC}} \)
This is the frequency at which the circuit will naturally oscillate with the largest amplitude. It’s like hitting the sweet spot on a drum to get the loudest sound.
At the resonant frequency, the circuit is most efficient. It’s like being able to hear a clear, strong note among many. This is super useful in electronics for things like tuning a radio to your favorite station without interference from others.
The resonant frequency is when our LCR circuit ‘sings’ most loudly. It’s a fundamental concept in electronics that helps us design systems to respond to specific frequencies while ignoring others.
Quality Factor of a Series LCR Circuit
Think of the Q Factor as a measure of how “pure” and “sharp” a bell’s ring is. If you strike a bell and it rings clearly with a single, pure tone that lasts a long time, it has a high Q Factor. If the bell’s ring is dull and fades quickly, it has a low Q Factor.
The quality factor, or Q factor, is a measure of how “sharp” the resonance is in a circuit. It’s defined as the ratio of the resonant frequency to the bandwidth over which the circuit can operate effectively. A higher Q factor means the circuit is more selective and can differentiate between closely spaced frequencies.
In an LCR circuit, the Q Factor tells us how well the circuit can pick out a single frequency from a complex mixture of different frequencies. It’s like having a super selective ear that can hear just one note in a noisy room.
The Q Factor is calculated using the formula:
\(\displaystyle Q = \frac{\text{Resonant Frequency (f₀)}}{\text{Bandwidth (Δf)}} \)
This means that a high Q Factor circuit can differentiate between frequencies that are very close together, while a low Q Factor circuit might get them mixed up¹.
A high Q Factor is important in applications like radio receivers, where you want to tune into one station without interference from others. It’s also crucial in musical instruments, where you want each note to be clear and distinct.
In a series LCR circuit, the Q Factor is particularly important at the resonant frequency—where the circuit naturally vibrates. At this frequency, the energy swings back and forth between the inductor (L) and the capacitor (C), with the resistor (R) controlling how quickly the energy is lost as heat.
The Q Factor gives us a quick way to understand how “sharp” the circuit is at its resonant frequency. A high Q means a sharp, selective circuit, while a low Q means a broader, less selective circuit. It’s all about how well the circuit can focus on one frequency and ignore the rest.
Understanding the Q Factor:
The Q Factor in a series LCR circuit is a measure of the sharpness of the resonance peak at the circuit’s natural resonant frequency. It tells us how narrow or wide the resonance is, which is important for applications like tuning circuits where we want precision.
In a series LCR circuit, the inductive reactance (XL) and capacitive reactance (XC) are given by:
\(\displaystyle X_L = 2\pi fL \)
\(\displaystyle X_C = \frac{1}{2\pi fC} \)
At the resonant frequency (f0), these two reactances are equal, so:
\(\displaystyle X_L = X_C \)
\(\displaystyle 2\pi f_0 L = \frac{1}{2\pi f_0 C} \)
Solving for (f0), we get the resonant frequency:
\(\displaystyle f_0 = \frac{1}{2\pi\sqrt{LC}} \)
The bandwidth (Δf) of the resonance is the range of frequencies over which the circuit can operate effectively. It’s defined as the difference between the frequencies at which the power is half its maximum value. At these points, the impedance of the circuit is (\(\displaystyle R\sqrt{2} \)).
The Q Factor is the ratio of the resonant frequency to the bandwidth:
\(\displaystyle Q = \frac{f_0}{\Delta f} \)
Now, we know that at resonance, the impedance (Z) of the circuit is purely resistive and equal to (R). The bandwidth is related to resistance and reactance by:
\(\displaystyle \Delta f = \frac{R}{2\pi L} \)
Substituting (∆f) in the Q Factor formula, we get:
\(\displaystyle Q = \frac{f_0}{\Delta f} = \frac{1}{2\pi\sqrt{LC}} \cdot \frac{2\pi L}{R} \)
Simplifying this, we arrive at the expression for the Q Factor:
\(\displaystyle Q = \frac{1}{R} \sqrt{\frac{L}{C}} \)
This expression tells us that the Q Factor is inversely proportional to the resistance and depends on the square root of the ratio of the inductance to the capacitance. A higher inductance or lower capacitance (and vice versa) will increase the Q Factor, as will a lower resistance.
How can we increase the Q Factor in an LCR circuit?
To increase the Q Factor in an LCR circuit, you can consider the following methods:
- Reduce Resistance: The Q Factor is inversely proportional to the resistance in the circuit. Using wires with a larger diameter (smaller gauge) for the inductor can reduce resistance, leading to a higher Q Factor.
- High-Quality Components: Choose capacitors and inductors with lower inherent losses. High-quality components typically have better performance characteristics and contribute to a higher Q Factor.
- Inductor Design: The design of the inductor, including the core material and the number of turns, can affect the Q Factor. A well-designed inductor that minimizes losses can increase the Q Factor.
- Circuit Layout: The physical layout of the circuit can also impact the Q Factor. Keeping leads short and avoiding parasitic capacitance and inductance can help maintain a high Q Factor.
Remember, a higher Q Factor results in a sharper resonance peak, which means the circuit will be more selective in its frequency response. This is particularly useful in applications like radio tuners and audio equipment, where you want to isolate specific frequencies.
How does damping affect the Q Factor?
Damping in an LCR circuit refers to the loss of energy over time, which can be due to resistance in the circuit or other factors like the radiation of energy. Now, let’s see how damping affects the Q Factor:
Damping is like the friction that slows down a swinging pendulum. In an LCR circuit, it’s the resistance that ‘calms’ the electrical oscillations. The more damping you have, the quicker the energy in the circuit dies out.
Impact on the Q Factor: The Q Factor is a measure of how long the circuit can oscillate before the energy is lost. Here’s what happens when you change the damping:
- Increased Damping: More energy is lost per cycle, which means the oscillations die out faster. This results in a lower Q Factor because the circuit becomes less selective about the frequencies it can pick up.
- Decreased Damping: Less energy is lost per cycle, so the oscillations last longer. This leads to a higher Q Factor, making the circuit more selective and able to resonate more sharply at a particular frequency.
Finding the right amount of damping is crucial. Too much damping and the circuit won’t resonate properly. Too little, and it might resonate too much at unwanted frequencies. It’s all about striking a balance for the desired application.
So in simple terms, damping affects the Q Factor by determining how quickly the energy in the circuit dissipates. More damping means a lower Q Factor and less selectivity, while less damping means a higher Q Factor and greater selectivity.
Power Dissipated in a Series LCR Circuit
First, imagine you’re running on a track. You use your energy to move forward, but some of it is lost due to friction with the ground and air resistance. In an electrical circuit, power dissipation is similar—it’s the energy that’s not used for work but is converted into heat.
The power dissipated in the resistor (R) is given by the formula:
\(\displaystyle P = I^2R \)
where (P) is the power in watts, (I) is the current in amperes, and (R) is the resistance in ohms.
At the resonant frequency, the inductor and capacitor pass energy back and forth perfectly, and the circuit behaves as if it’s just a resistor. This is when the power dissipation is at its maximum because the impedance is at its minimum, and the current is at its peak.
Power dissipation in a circuit is the energy converted to heat per unit of time. In a series LCR circuit, this happens due to the resistor.
The voltage supplied to an LCR circuit is usually an AC voltage, which can be represented as:
\(\displaystyle V = V_{\text{RMS}} \sqrt{2} \sin(\omega t) \)
where (VRMS) is the root mean square (RMS) voltage, and (ω) is the angular frequency of the AC source. The current that flows through the circuit can also be represented in a similar sinusoidal form. At the resonant frequency, the impedance is purely resistive, so the current is in phase with the voltage.
Since the current and voltage are in phase, we can relate the RMS current to the RMS voltage by Ohm’s law:
\(\displaystyle I_{\text{RMS}} = \frac{V_{\text{RMS}}}{R} \)
Substituting (IRMS) into the power formula, we get:
\(\displaystyle P = \left(\frac{V_{\text{RMS}}}{R}\right)^2R \)
Simplifying this, we arrive at the expression for the power dissipated:
\(\displaystyle P = \frac{V_{\text{RMS}}^2}{R} \)
This is the power dissipated in the resistor of a series LCR circuit, and it shows how the power depends on the RMS voltage and the resistance.
In real-world applications, managing power dissipation is crucial. For example, in electronic devices, too much heat can damage components. That’s why devices have heat sinks and fans to manage the power that’s dissipated.
Power dissipation in a series LCR circuit is all about how the resistor turns electrical energy into heat. It’s a fundamental concept that helps us understand and design circuits for everything from radios to computers.
How does the Q Factor affect power dissipation in LCR circuits?
The Q Factor, or Quality Factor, has a significant impact on power dissipation in LCR circuits. Here’s how it works:
High Q Factor:
- A high Q Factor indicates that the circuit has low damping and is less lossy. This means the circuit stores more energy compared to the energy it dissipates over each cycle.
- Such circuits are underdamped, which leads to less power being dissipated as heat and more energy being stored in the reactive components (inductors and capacitors).
- If driven at the resonant frequency, high-Q circuits can experience large amplitude oscillations because they are very selective about the frequency they resonate at.
Low Q Factor:
- A low Q Factor means the circuit has more damping and is more lossy. It dissipates more energy as heat over each cycle compared to the energy it stores.
- These circuits are overdamped, leading to greater power dissipation in the resistor and less energy stored in the reactive components.
- Low-Q circuits tend to have a broader bandwidth and are less prone to large amplitude oscillations at resonance.
Understanding the relationship between the Q Factor and power dissipation helps in designing circuits with the desired characteristics for specific applications, such as filters or oscillators.
Applications of LCR Circuits
Applying AC voltage to a Series LCR circuit has several practical applications due to its ability to resonate at specific frequencies and filter signals. Here are some of the key applications:
- Signal Tuning: One of the most common uses is in tuning circuits, such as those found in radios and TVs, where the circuit can select a specific frequency from a range of different frequencies.
- Filters: LCR circuits can act as various types of filters (low-pass, high-pass, band-pass, and band-stop), which are essential in audio equipment to control the frequencies that reach the speakers.
- Oscillators: These circuits are used to create oscillators that generate a signal at a particular frequency. Oscillators are fundamental in devices like signal generators, clocks, and watches.
- Impedance Matching: LCR circuits can be used to match the impedance between different parts of an electronic system, ensuring maximum power transfer and efficient operation.
- Voltage Regulation: They help in voltage regulation by providing a constant voltage output from a variable input supply, which is crucial for the stable operation of electronic devices.
- Surge Protection: LCR circuits can protect against voltage surges in power supplies by absorbing and dissipating excess energy.
- Medical Equipment: In medical devices, such as electrocardiograms (ECGs), LCR circuits are used to filter out unwanted noise and interference, ensuring accurate readings.
- Telecommunications: They are used in telecommunication systems for filtering signals and for frequency synthesis in transmitters and receivers.
These applications showcase the versatility of Series LCR circuits when subjected to AC voltage, making them a fundamental component in many electronic devices and systems.
Also Read: Resonance
Solved Examples
Problem 1: Calculate the impedance of a series LCR circuit with (R = 10 Ω), (L = 0.1 H), and (C = 100 µF ) connected to an AC source of frequency (50 Hz).
Solution: Given:
- (R = 10 Ω)
- (L = 0.1 H)
- (\(\displaystyle C = 100 \mu F = 100 \times 10^{-6} \, F \))
- (f = 50 Hz)
First, calculate the inductive reactance (XL) and capacitive reactance (XC):
\(\displaystyle X_L = 2\pi f L = 2\pi \times 50 \times 0.1 = 31.4 \, \Omega \)
\(\displaystyle X_C = \frac{1}{2\pi f C} = \frac{1}{2\pi \times 50 \times 100 \times 10^{-6}} = 31.83 \, \Omega \)
The impedance ( Z ) of the series LCR circuit is given by:
\(\displaystyle Z = \sqrt{R^2 + (X_L – X_C)^2} \)
\(\displaystyle Z = \sqrt{10^2 + (31.4 – 31.83)^2}\)
\(\displaystyle Z = \sqrt{100 + (-0.43)^2} \)
\(\displaystyle Z = \sqrt{100 + 0.1849}\)
\(\displaystyle Z = \sqrt{100.1849} \)
\(\displaystyle Z \approx 10.01 \, \Omega \)
The impedance of the series LCR circuit is (10.01 Ω).
Problem 2: Determine the resonant frequency of a series LCR circuit with (L = 2 H) and (C = 50 µF).
Solution: Given:
- (L = 2 H)
- (\(\displaystyle C = 50 \mu F = 50 \times 10^{-6} \, F \))
The resonant frequency (f0) is given by:
\(\displaystyle f_0 = \frac{1}{2\pi \sqrt{LC}} \)
\(\displaystyle f_0 = \frac{1}{2\pi \sqrt{2 \times 50 \times 10^{-6}}} \)
\(\displaystyle f_0 = \frac{1}{2\pi \sqrt{100 \times 10^{-6}}} \)
\(\displaystyle f_0 = \frac{1}{2\pi \times 0.01} \)
\(\displaystyle f_0 = \frac{1}{0.02\pi} \)
\(\displaystyle f_0 \approx 7.96 \, \text{Hz} \)
The resonant frequency of the series LCR circuit is approximately (7.96 Hz).
Problem 3: In a series LCR circuit with (R = 50 Ω), (L = 0.5 H), and (C = 20 µF), connected to an AC source with peak voltage (V0 = 100 V) and frequency (f = 50 Hz), calculate the voltage across the resistor at resonance.
Solution: Given:
- (R = 50 Ω)
- (L = 0.5 H)
- (\(\displaystyle C = 20 \mu F = 20 \times 10^{-6} \, F \))
- (V0 = 100 V)
- (f = 50 Hz)
At resonance, the inductive reactance (XL) and capacitive reactance (XC) cancel each other, and the impedance (Z) of the circuit is purely resistive:
XL = XC
The voltage across the resistor (VR) is equal to the source voltage (V0) because the impedance is purely resistive:
\(\displaystyle V_R = V_0\)
The voltage across the resistor at resonance is (100 V).
Problem 4: Calculate the quality factor (Q factor) of a series LCR circuit with (R = 20 Ω), (L = 0.1 H), and (C = 50 µF).
Solution: Given:
- (R = 20 Ω)
- (L = 0.1 H)
- (\(\displaystyle C = 50 \mu F = 50 \times 10^{-6} \, F \))
The quality factor (Q) is given by:
\(\displaystyle Q = \frac{1}{R} \sqrt{\frac{L}{C}} \)
\(\displaystyle Q = \frac{1}{20} \sqrt{\frac{0.1}{50 \times 10^{-6}}} \)
\(\displaystyle Q = \frac{1}{20} \sqrt{2000} \)
\(\displaystyle Q = \frac{1}{20} \times 44.72 \)
Q = 2.24
The quality factor of the series LCR circuit is (2.24).
Problem 5: An AC source with RMS voltage (VRMS = 100 V ) is connected to a series LCR circuit with (R = 10 Ω), (L = 0.2 H), and (C = 40 µF ). Calculate the power dissipated in the circuit at resonance.
Solution: Given:
- (VRMS = 100 V)
- (R = 10 Ω)
- (L = 0.2 H)
- (\(\displaystyle C = 40 \mu F = 40 \times 10^{-6} \, F \))
At resonance, the power dissipated (P) in the circuit is given by:
\(\displaystyle P = \frac{V_{\text{RMS}}^2}{R} \)
\(\displaystyle P = \frac{100^2}{10} \)
\(\displaystyle P = \frac{10000}{10} \)
P = 1000 W
The power dissipated in the series LCR circuit at resonance is (1000 W).
Problem 6: A series LCR circuit with (R = 5 Ω), (L = 0.1 H), and (C = 25 µF) is connected to an AC source with RMS voltage (VRMS = 50 V) and frequency (f = 60 Hz). Calculate the RMS current through the circuit.
Solution: Given:
- (R = 5 Ω)
- (L = 0.1 H)
- (\(\displaystyle C = 25 \mu F = 25 \times 10^{-6} \, F \))
- (VRMS = 50 V)
- (f = 60 Hz)
First, calculate the inductive reactance (XL) and capacitive reactance (XC):
\(\displaystyle X_L = 2\pi f L = 2\pi \times 60 \times 0.1 = 37.7 \, \Omega \)
\(\displaystyle X_C = \frac{1}{2\pi f C} = \frac{1}{2\pi \times 60 \times 25 \times 10^{-6}} = 106.1 \, \Omega \)
The impedance (Z) of the circuit is given by:
\(\displaystyle Z = \sqrt{R^2 + (X_L – X_C)^2} \)
\(\displaystyle Z = \sqrt{5^2 + (37.7 – 106.1)^2} \)
\(\displaystyle Z = \sqrt{25 + (-68.4)^2} \)
\(\displaystyle Z = \sqrt{25 + 4678.56} \)
\(\displaystyle Z = \sqrt{4703.56} \)
\(\displaystyle Z \approx 68.58 \, \Omega \)
The RMS current (IRMS) is:
\(\displaystyle I_{\text{RMS}} = \frac{V_{\text{RMS}}}{Z} \)
\(\displaystyle I_{\text{RMS}} = \frac{50}{68.58} \)
\(\displaystyle I_{\text{RMS}} \approx 0.73 \, \text{A} \)
The RMS current through the series LCR circuit is (0.73 A).
FAQs
What is a Series LCR Circuit, and how does it differ from other types of circuits?
A Series LCR Circuit consists of a resistor R, an inductor L, and a capacitor C connected in series to an AC voltage source. It differs from other circuits in that it incorporates all three passive components (resistor, inductor, and capacitor) in series.
How does the impedance of a Series LCR Circuit change with frequency?
The impedance Z of a Series LCR Circuit changes with frequency due to the inductor and capacitor’s varying reactances XL and XC, respectively. The inductive reactance dominates at low frequencies, while the capacitive reactance dominates at high frequencies.
What is resonance in a Series LCR Circuit, and how is it achieved?
Resonance in a Series LCR Circuit occurs when the inductive reactance XL equals the capacitive reactance XC, resulting in minimum impedance Z and maximum current flow. It is achieved by adjusting the frequency of the applied AC voltage to match the natural frequency of the circuit.
How does the phase relationship between voltage and current change in a Series LCR Circuit as frequency varies?
At resonance, the phase difference between voltage and current in a Series LCR Circuit is zero, indicating that they are in phase. However, as the frequency deviates from resonance, the phase difference increases, with the current either lagging or leading the voltage depending on the frequency.
What is the quality factor (Q-factor) of a Series LCR Circuit, and how is it calculated?
The quality factor Q of a Series LCR Circuit is a measure of its selectivity or efficiency. It is calculated as the ratio of reactance to resistance, \(\displaystyle Q = \frac{X}{R}\), where (X) is the reactance (either inductive or capacitive) and (R) is the resistance.
How does the presence of an inductor and capacitor affect the overall behavior of a Series LCR Circuit?
The presence of an inductor and capacitor in a Series LCR Circuit leads to resonance, where the circuit exhibits maximum current flow and minimum impedance at a specific frequency. Additionally, the inductor and capacitor contribute reactively to the impedance of the circuit, affecting its overall behavior.
What are the applications of Series LCR Circuits in real-life scenarios?
Series LCR Circuits find applications in various electrical and electronic systems, including filters, oscillators, tuned circuits in radios, impedance-matching networks, and power factor correction circuits. They are essential components in signal processing, communications, and power distribution systems.