Alpha Decay

Alpha decay was first discovered by Ernest Rutherford in the early 20th century. While studying radioactivity, he found that certain elements emitted a type of radiation that could be blocked by just a sheet of paper or even the skin. This was unlike other forms of radiation, such as beta or gamma rays, which required denser materials to be stopped.

Rutherford identified these emissions as helium nuclei, which consist of two protons and two neutrons, and named them “alpha particles.” He realized that these particles were being emitted by the nuclei of heavy elements like uranium and thorium as they transformed into other elements. This process was later named “alpha decay,” and it was one of the first types of nuclear reactions to be understood.

The discovery of alpha decay was significant because it provided early evidence for the existence of the nucleus in atoms and led to the development of nuclear physics as a field. It also helped scientists understand the natural process by which some elements can transform into others, shedding light on the complex behaviors of atomic structures.

What is Alpha Decay?

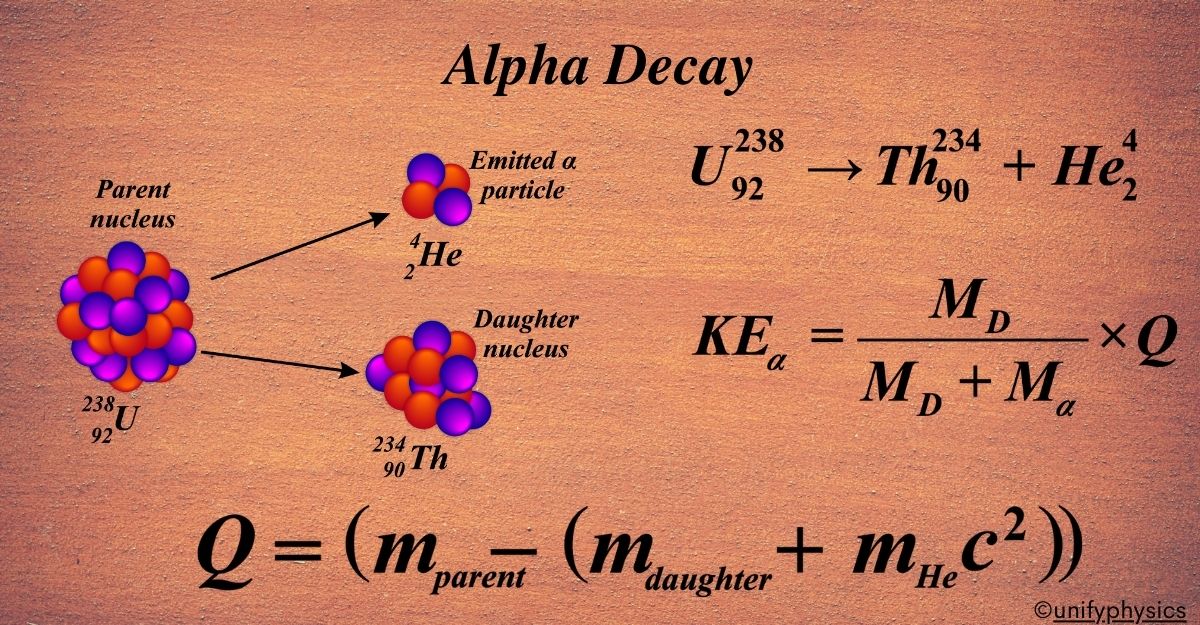
Alpha decay is a type of radioactive decay where an unstable atomic nucleus emits an alpha particle (consisting of two protons and two neutrons) and transforms into a lighter nucleus. Alpha decay is a process that occurs in certain heavy, unstable atomic nuclei. In this process, the nucleus releases energy by emitting an alpha particle, which is essentially a helium-4 nucleus composed of two protons and two neutrons bound together.

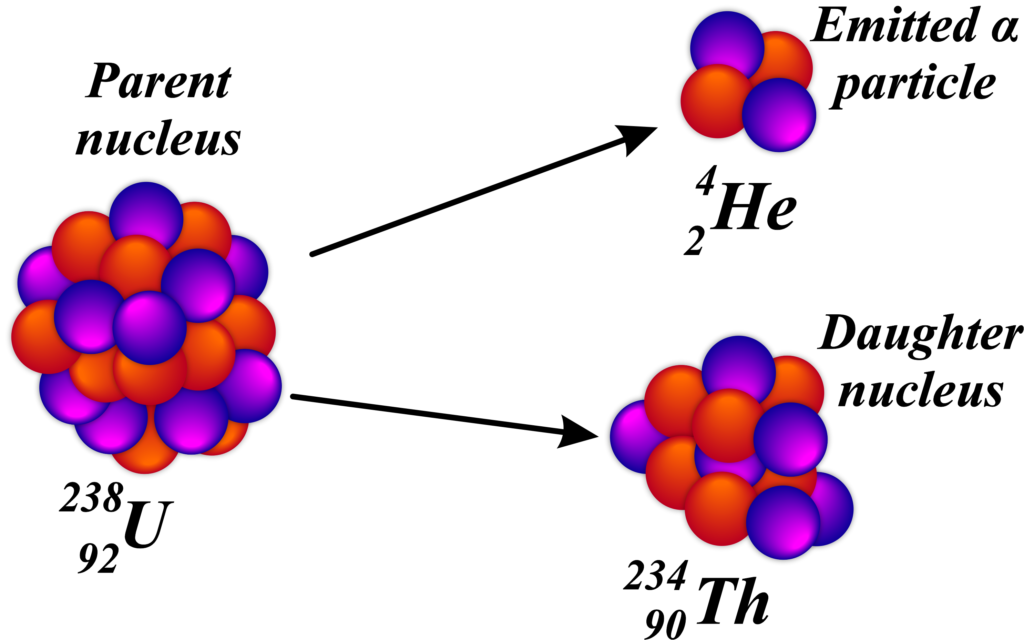
Imagine the nucleus of an atom as a crowded room where particles are held together tightly. Over time, some particles find a way to escape the room to reduce the crowding. In alpha decay, it’s like two protons and two neutrons hold hands and jump out together, leaving behind a less crowded and more stable room (the daughter nucleus).

This emission of an alpha particle transforms the original atom into a new atom with two fewer protons and two fewer neutrons. Because the number of protons determines the element, the atom changes into a different element after alpha decay.

Alpha decay typically happens in very heavy elements like uranium or radium, where the nucleus has so many protons and neutrons that it’s unstable. By emitting an alpha particle, the nucleus reaches a more stable state with lower energy.

Alpha Decay Equation

The alpha decay equation is a way to represent the process of alpha decay in a nuclear reaction. It shows how an unstable nucleus (the parent) emits an alpha particle and transforms into a different nucleus (the daughter).

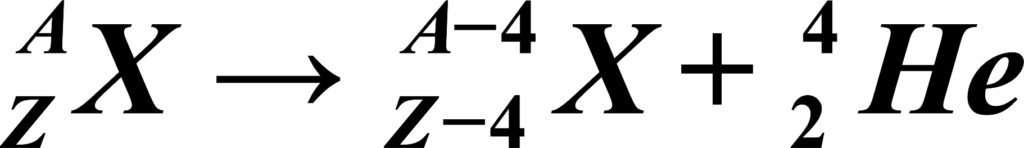
Start with the parent nucleus, which is represented by its atomic number (Z) and mass number (A). The atomic number is the number of protons, and the mass number is the total number of protons and neutrons. An alpha particle is always represented by the symbol (\(\displaystyle ^{4}_{2}He \)), which means it has 2 protons and 2 neutrons (a total mass number of 4).

After the alpha particle is emitted, the daughter nucleus will have 2 fewer protons and 2 fewer neutrons than the parent. So, its atomic number will be (Z – 2) and its mass number will be (A – 4).

For example, let’s look at the alpha decay of uranium-238:

\(\displaystyle ^{238}{92}U \rightarrow ^{234}{90}Th + ^{4}_{2}He \)

In this equation:

• Uranium-238 (the parent) has 92 protons and 238 total nucleons.
• After emitting an alpha particle, it becomes thorium-234 (the daughter), with 90 protons and 234 total nucleons.
• The alpha particle is the (\(\displaystyle ^{4}_{2}He \)) on the right side of the equation.

This equation helps us keep track of the particles involved in the decay and ensures that both mass and atomic numbers are conserved.

Momentum Conservation in Alpha Decay

The law of conservation of momentum states that the total momentum before and after decay must be equal. This principle also applies to alpha decay. Since the alpha particle and daughter nucleus move in opposite directions, their momenta are equal in magnitude but opposite in direction.

Before the decay, the parent nucleus is at rest, so its momentum is zero. During alpha decay, the parent nucleus emits an alpha particle. This particle carries away some of the nucleus’s mass and energy. To conserve momentum, the daughter nucleus must recoil in the opposite direction to the alpha particle. This recoil is much smaller than the alpha particle’s motion because the daughter nucleus is much heavier.

Think of it like a gun firing a bullet:

• The bullet (alpha particle) speeds off in one direction.
• The gun (daughter nucleus) recoils backward.
• The total momentum before and after the shot is the same.

In mathematical terms, if (p) represents momentum, (m) represents mass, and (v) represents velocity, then for the alpha particle and daughter nucleus:

\(\displaystyle p_{\text{parent}} = p_{\text{alpha}} + p_{\text{daughter}} \)

\(\displaystyle 0 = m_{\text{alpha}} \times v_{\text{alpha}} + m_{\text{daughter}} \times v_{\text{daughter}} \)

Since (m_daughter) is much larger than (m_alpha), (v_daughter) must be much smaller than (v_alpha) to keep the equation balanced. This concept ensures that even though individual particles move during alpha decay, the overall system’s momentum remains unchanged.

If external forces are present during alpha decay, they can affect the momentum of the particles after the decay. However, within the nucleus itself, the process of alpha decay is not significantly influenced by external forces because it is governed by strong nuclear forces, which are much stronger than any typical external force.

The alpha particle and daughter nucleus would still be emitted with a certain momentum based on the energy of the decay. External forces could then act on these particles after they have been emitted, changing their velocities and thus their momenta. The total momentum of the system (including the alpha particle, daughter nucleus, and any other objects interacting with them) would still be conserved, but it would be distributed differently due to the external forces.

For example, if an alpha particle is emitted in space where gravitational forces are acting, its trajectory might curve due to gravity. Similarly, if it passes through an electric or magnetic field, its path could be deflected. However, these changes occur after the alpha decay process has already happened. The decay itself occurs within the nucleus and is not directly affected by external forces.

Q Value of Alpha Decay

The Q value of alpha decay represents the amount of energy released when an atomic nucleus emits an alpha particle. It’s a crucial concept because it tells us how much energy is involved in the decay process.

Think of the nucleus as a tightly bound cluster of protons and neutrons. It takes energy to hold them together, which is called the binding energy. When a nucleus undergoes alpha decay, it loses a bit of its mass in the form of the emitted alpha particle.

According to Einstein’s famous equation (\(\displaystyle E=mc^2 \)), mass can be converted into energy. So, the lost mass turns into energy that is released during the decay. The Q value is the energy difference between the initial state (before decay) and the final state (after decay).

Mathematically, if (M_parent) is the mass of the parent nucleus, (M_daughter) is the mass of the daughter nucleus, and (M_alpha) is the mass of the alpha particle, then:

\(\displaystyle Q = (M_{\text{parent}} – (M_{\text{daughter}} + M_{\text{alpha}}))c^2 \)

This equation shows that if the combined mass of the daughter nucleus and alpha particle is less than that of the parent nucleus, then (Q) will be positive, indicating that energy is released.

The Q value gives us a measure of how “energetic” or “powerful” an alpha decay process is. A higher Q value means more energy is released, which can have various implications for how that energy affects surrounding materials or detection equipment.

The mass of a nucleus is always less than the sum of the masses of its protons and neutrons due to binding energy. This difference is called the mass defect. In alpha decay, a parent nucleus (P) decays into a daughter nucleus (D) and an alpha particle (α). We need to consider the masses of these particles:

• (M_P): Mass of the parent nucleus
• (M_D): Mass of the daughter nucleus
• (M_α): Mass of the alpha particle

The total energy before and after the decay must be equal. Before decay, we have the rest mass energy of the parent nucleus. After decay, we have the rest mass energies of the daughter nucleus and alpha particle, plus the kinetic energy released. The energy before decay is simply the rest mass energy of the parent nucleus:

\(\displaystyle E_{\text{initial}} = M_P c^2 \)

The energy after decay is the sum of the rest mass energies of the daughter nucleus and alpha particle, plus their kinetic energies (KE_D) and (KE_α) respectively):

\(\displaystyle E_{\text{final}} = M_D c^2 + KE_D + M_\alpha c^2 + KE_\alpha \)

Since energy is conserved, we set ( E_initial) equal to (E_final):

\(\displaystyle M_P c^2 = M_D c^2 + KE_D + M_\alpha c^2 + KE_\alpha \)

The Q value is defined as the kinetic energy released during decay, so it’s equal to (KE_D + KE_α). Rearranging our equation gives us:

\(\displaystyle Q = (M_P – (M_D + M_\alpha))c^2 \)

This is our derived expression for the Q value in alpha decay. It shows that the Q value is equal to the difference in rest mass energies (multiplied by (c²) between the initial and final states. Remember that in practice, we often use atomic mass units (u) for these calculations, and since 1 u corresponds to a certain amount of energy (931.5 MeV), we can directly convert mass differences into energy without always multiplying by (c^2).

Example: Suppose we have a parent nucleus of Uranium-238 that undergoes alpha decay to form Thorium-234 and an alpha particle (Helium-4).

Given: Identify the Masses

• Mass of Uranium-238 (\(\displaystyle ( M_{U-238} \)): 238.050788 u
• Mass of Thorium-234 (\(\displaystyle ( M_{Th-234} \)): 234.043601 u
• Mass of Helium-4 (\(\displaystyle( M_{He-4} \)): 4.002603 u

\(\displaystyle Q = (M_{U-238} – (M_{Th-234} + M_{He-4})) \times 931.5 \text{ MeV/u} \)

\(\displaystyle Q = (238.050788 \text{ u} – (234.043601 \text{ u} + 4.002603 \text{ u})) \times 931.5 \text{ MeV/u} \)

\(\displaystyle Q = (238.050788 \text{ u} – 238.046204 \text{ u}) \times 931.5 \text{ MeV/u} \)

\(\displaystyle Q = 0.004584 \text{ u} \times 931.5 \text{ MeV/u} \)
\(\displaystyle Q = 4.27 \text{ MeV} \)

So, the Q value for the alpha decay of Uranium-238 is approximately 4.27 MeV. This means that when Uranium-238 decays to Thorium-234 and an alpha particle, about 4.27 MeV of energy is released as kinetic energy shared between the Thorium-234 nucleus and the alpha particle.

Significance of a positive or negative Q value:

The Q value in nuclear reactions indicates whether the reaction releases energy (exothermic) or absorbs energy (endothermic).

Positive Q Value: A positive Q value means that the reaction releases energy. This occurs when the total mass of the products is less than the total mass of the reactants, resulting in a mass defect that is converted into energy (according to (\(\displaystyle E=mc^2 \)). In alpha decay, a positive Q value implies that the decay process is spontaneous and will occur without any external energy input. The released energy is usually carried away by the products of the reaction as kinetic energy.

Negative Q Value: A negative Q value means that the reaction requires an input of energy to occur. This happens when the total mass of the products is greater than the total mass of the reactants, so energy must be supplied to make up for the mass increase. In alpha decay, a negative Q value would mean that the decay cannot happen spontaneously; it would require an external source of energy to proceed.

A positive Q value signifies a spontaneous and energetically favorable reaction, while a negative Q value indicates a non-spontaneous reaction that needs external energy to take place.

Zero Q value: If the Q value of a nuclear reaction is exactly zero, it means that the total mass of the reactants is equal to the total mass of the products. In this case, no energy is released or absorbed during the reaction.

The reaction is said to be in a state of energy balance or “break-even.” Since there’s no energy release, there’s no kinetic energy imparted to the products. For a reaction with a Q value of zero to occur, it would require precise conditions where the reactants have just enough kinetic energy to overcome the repulsive forces and allow the reaction to proceed. In practice, such conditions are extremely rare and delicate, making reactions with a Q value of zero very unlikely to occur naturally.

In alpha decay, if the Q value were zero, it would mean that the alpha particle would be emitted with no kinetic energy, which is not observed in nature. Alpha particles are always emitted with some kinetic energy, indicating that alpha decay has a positive Q value.

Kinetic Energy In Alpha Decay: In alpha decay, the kinetic energy released (as indicated by the positive Q value) is shared between the daughter nucleus and the alpha particle. Here’s how it’s distributed:

• Conservation of Momentum: Because momentum is conserved in the decay process, the momentum gained by the alpha particle must be equal and opposite to that gained by the daughter nucleus.
• Inverse Mass Relationship: The distribution of kinetic energy between the two products is inversely proportional to their masses. This means that the lighter alpha particle gets a larger share of the kinetic energy, while the heavier daughter nucleus gets a smaller share.

Mathematically, if (KE_α) is the kinetic energy of the alpha particle and (KE_D) is the kinetic energy of the daughter nucleus, then:

\(\displaystyle KE_\alpha = \frac{M_D}{M_D + M_\alpha} \times Q \)

\(\displaystyle KE_D = \frac{M_\alpha}{M_D + M_\alpha} \times Q \)

Where (M_D) is the mass of the daughter nucleus and (M_α) is the mass of the alpha particle.

The alpha particle, being much lighter than the daughter nucleus, moves away at a higher speed due to its larger share of kinetic energy. This kinetic energy can be detected and measured using various instruments, such as cloud chambers or semiconductor detectors, which helps us understand and confirm the principles of nuclear decay.

The kinetic energy carried away by these particles can cause ionization or excitation of atoms in a medium if they collide with them, which is why alpha particles can be harmful if ingested or inhaled.

Gamow Theory of Alpha Decay

Proposed by George Gamow in 1928, this theory explains alpha decay using quantum mechanics. It suggests that alpha particles tunnel through a potential barrier (the nuclear force holding them inside the nucleus) due to their wave-like properties.

The Gamow Theory, also known as the quantum mechanical theory of alpha decay, was developed by George Gamow in 1928. It explains the alpha decay process using the principles of quantum mechanics.

In the nucleus, alpha particles are trapped in a potential well created by the strong nuclear force. When an alpha particle approaches the edge of the nucleus, it encounters a Coulomb barrier, which is a potential energy barrier due to the repulsion between the positively charged alpha particle and the positively charged protons in the nucleus.

According to quantum mechanics, particles like alpha particles have wave-like properties and can be described by a wave function. Even if an alpha particle doesn’t have enough energy to climb over the Coulomb barrier (like a ball rolling over a hill), it can still ‘tunnel’ through it due to its wave nature.

The probability of tunneling, and thus the rate of alpha decay, can be calculated using Gamow’s equation:

\(\displaystyle P = e^{-2G} \)

Where (P) is the probability of tunneling, and (G) is the Gamow factor given by:

\(\displaystyle G = \frac{2\pi Z e^2}{\hbar} \sqrt{\frac{m}{2E}} \)

• (Z) is the atomic number of the daughter nucleus.
• (e) is the elementary charge.
• ( \(\displaystyle\hbar\)) is the reduced Planck’s constant.
• (m) is the mass of the alpha particle.
• (E) is the kinetic energy of the alpha particle.

The higher the Gamow factor (G), the lower the probability of tunneling. The probability decreases exponentially with increasing nuclear charge and decreasing particle energy. This equation helps explain why heavier nuclei (with higher (Z) have lower decay rates.

The Gamow Theory provides a quantum mechanical explanation for why alpha particles can escape from nuclei despite not having enough classical energy to overcome the Coulomb barrier. It’s a beautiful example of how quantum mechanics can explain phenomena that classical physics cannot.

Safety Level of Alpha Decay

Alpha decay is a type of radioactive decay in which an unstable atomic nucleus emits an alpha particle (consisting of two protons and two neutrons) and transforms into a lighter nucleus. Alpha particles are not deeply penetrating and can be stopped by skin or paper. However, if alpha-emitting substances are ingested or inhaled, they can be harmful due to their high ionization power. When it comes to safety, alpha particles have some unique characteristics:

Low Penetration Power: Alpha particles are relatively heavy and carry a double positive charge. Due to their mass and charge, they have low penetration power and can be stopped by a sheet of paper, the outer layer of human skin, or even a few centimeters of air.

Internal vs. External Hazard: Externally, alpha particles are not a significant hazard because they cannot penetrate the skin to reach sensitive internal organs. Internally, if alpha-emitting materials are ingested or inhaled, they can be hazardous. Inside the body, alpha particles can cause significant damage to living cells due to their high ionization power.

Ionization: Alpha particles can ionize atoms and molecules along their path, leading to biological damage. The ionization can cause cell death or mutations, which may lead to cancer or other health issues.

Safety Precautions:

• To ensure safety from alpha radiation, it is important not to ingest or inhale alpha-emitting substances.
• Laboratories and facilities that handle alpha-emitting materials use protective gear and proper ventilation systems to prevent inhalation or ingestion.
• Monitoring devices are used to detect any release of alpha radiation in the environment.

Alpha particles pose little external threat due to their low penetration power, they can be quite dangerous if they enter the body. Therefore, safety measures focus on preventing the ingestion or inhalation of alpha-emitting substances.

Also Read: Atomic Mass and Composition of Nucleus

Uses of Alpha Decay

Smoke Detectors: Many smoke detectors use a small amount of americium-241, an alpha-emitting isotope. The alpha particles ionize the air in a small detection chamber, allowing a current to flow. When smoke enters the chamber, it disrupts the flow of ions, reducing the current and triggering the alarm.

Radioisotope Thermoelectric Generators (RTGs): RTGs are used to provide power in space missions, remote locations, or situations where regular maintenance is not possible. They contain alpha-emitting isotopes like plutonium-238, which release heat through alpha decay. This heat is converted into electricity using thermocouples, providing a reliable power source for spacecraft and remote facilities.

Medical Uses: Alpha-emitting isotopes are used in targeted cancer therapy. They can be attached to molecules that specifically target cancer cells. Once inside the cancer cells, the alpha particles can kill the cells due to their high ionization power.

Scientific Research: Alpha decay is used in scientific research to understand nuclear reactions and the structure of nuclei. It also helps in dating archaeological finds and geological formations through techniques like uranium-thorium dating.

Industrial Applications: Alpha particles can be used for quality control in the production of thin metallic films and semiconductors. They help in measuring the thickness of materials by detecting the amount of alpha radiation that passes through or is reflected.

Alpha decay finds uses in safety devices, power generation, medicine, scientific research, and industry due to its ionizing properties and the heat it generates.

Solved Examples

Problem 1: Write the alpha decay equation for Uranium-238.

Solution: In alpha decay, a nucleus emits an alpha particle (which is a helium nucleus, (\(\displaystyle ^4_2\text{He} \)), reducing its atomic number by 2 and its mass number by 4. The alpha decay of Uranium-238 can be represented as:

\(\displaystyle ^{238}_{92}\text{U} \rightarrow ^{234}_{90}\text{Th} + ^{4}_{2}\text{He} \)

The alpha decay equation for Uranium-238 is:

\(\displaystyle ^{238}_{92}\text{U} \rightarrow ^{234}_{90}\text{Th} + ^{4}_{2}\text{He} \)

Problem 2: A nucleus of Radium-226 undergoes alpha decay. If the alpha particle is emitted with a kinetic energy of 4.87 MeV, calculate the recoil speed of the daughter nucleus (Radon-222). Assume the mass of the alpha particle is 4 u and the mass of the Radon nucleus is 222 u.

Solution: Given,

• Kinetic energy of alpha particle (\(\displaystyle K_{\alpha} = 4.87 \, \text{MeV}\))
• Mass of alpha particle (\(\displaystyle m_{\alpha} = 4 \, \text{u} \))
• Mass of Radon nucleus (\(\displaystyle m_{\text{Rn}} = 222 \, \text{u} \))

First, convert kinetic energy to joules:

\(\displaystyle K_{\alpha} = 4.87 \, \text{MeV} \times 1.602 \times 10^{-13} \, \text{J/MeV} \)

\(\displaystyle K_{\alpha} = 7.8 \times 10^{-13} \, \text{J} \)

The momentum (p) of the alpha particle can be calculated using the kinetic energy:

\(\displaystyle K_{\alpha} = \frac{p^2}{2m_{\alpha}} \)

\(\displaystyle p = \sqrt{2m_{\alpha} K_{\alpha}} \)

Convert the mass of the alpha particle to kg:

\(\displaystyle m_{\alpha} = 4 \times 1.66 \times 10^{-27} \, \text{kg} \)

\(\displaystyle m_{\alpha} = 6.64 \times 10^{-27} \, \text{kg} \)

Calculate the momentum:

\(\displaystyle p = \sqrt{2 \times 6.64 \times 10^{-27} \, \text{kg} \times 7.8 \times 10^{-13} \, \text{J}} \)

\(\displaystyle p \approx 3.22 \times 10^{-19} \, \text{kg} \cdot \text{m/s} \)

By momentum conservation, the momentum of the alpha particle and the radon nucleus are equal in magnitude but opposite in direction. Therefore, the recoil speed (\(\displaystyle v_{\text{Rn}} \)) of the radon nucleus is:

\(\displaystyle p = m_{\text{Rn}} v_{\text{Rn}} \)

\(\displaystyle v_{\text{Rn}} = \frac{p}{m_{\text{Rn}}} \)

Convert the mass of the radon nucleus to kg:

\(\displaystyle m_{\text{Rn}} = 222 \times 1.66 \times 10^{-27} \, \text{kg} \)

\(\displaystyle m_{\text{Rn}} = 3.6852 \times 10^{-25} \, \text{kg} \)

Calculate the recoil speed:

\(\displaystyle v_{\text{Rn}} = \frac{3.22 \times 10^{-19} \, \text{kg} \cdot \text{m/s}}{3.6852 \times 10^{-25} \, \text{kg}} \)

\(\displaystyle v_{\text{Rn}} \approx 8.74 \times 10^5 \, \text{m/s} \)

The recoil speed of the Radon-222 nucleus is approximately (\(\displaystyle 8.74 \times 10^5 \)) m/s.

Problem 3: Calculate the Q value of the alpha decay of Polonium-210. The masses are:

• (\(\displaystyle ^{210}_{84}\text{Po} \)): 209.982873 u
• (\(\displaystyle ^{206}_{82}\text{Pb} \)): 205.974465 u
• (\(\displaystyle ^{4}_{2}\text{He} \)): 4.002603 u

Solution: The Q value of the reaction is the difference in the mass-energy of the parent nucleus and the sum of the mass energies of the daughter nucleus and the alpha particle.

\(\displaystyle Q = \left( m_{\text{parent}} – m_{\text{daughter}} – m_{\alpha} \right)c^2 \)

Convert the masses to energy (1 u = 931.5 MeV):

\(\displaystyle m_{\text{parent}} = 209.982873 \, \text{u} \)

\(\displaystyle m_{\text{daughter}} = 205.974465 \, \text{u} \)

\(\displaystyle m_{\alpha} = 4.002603 \, \text{u} \)

Calculate the mass difference:

\(\displaystyle \Delta m = m_{\text{parent}} – (m_{\text{daughter}} + m_{\alpha}) \)

\(\displaystyle \Delta m = 209.982873 – (205.974465 + 4.002603) \)

\(\displaystyle \Delta m = 209.982873 – 209.977068 \)

\(\displaystyle \Delta m = 0.005805 \, \text{u} \)

Convert the mass difference to energy:

\(\displaystyle Q = 0.005805 \, \text{u} \times 931.5 \, \text{MeV/u}\)

\(\displaystyle Q \approx 5.41 \, \text{MeV} \)

The Q value of the alpha decay of Polonium-210 is approximately 5.41 MeV.

Problem 4: Calculate the energy released when Radon-222 undergoes alpha decay. The atomic masses are:

• (\(\displaystyle ^{222}_{86}\text{Rn} \)): 222.017578 u
• (\(\displaystyle ^{218}_{84}\text{Po} \)): 218.008973 u
• (\(\displaystyle ^{4}_{2}\text{He} \)): 4.002603 u

Solution: The Q value for the decay is the difference in mass between the parent nucleus and the sum of the masses of the daughter nucleus and the alpha particle.

\(\displaystyle Q = \left( m_{\text{Rn}} – m_{\text{Po}} – m_{\alpha} \right)c^2 \)

Convert the masses to energy (1 u = 931.5 MeV):

\(\displaystyle m_{\text{Rn}} = 222.017578 \, \text{u} \)

\(\displaystyle m_{\text{Po}} = 218.008973 \, \text{u} \)

\(\displaystyle m_{\alpha} = 4.002603 \, \text{u} \)

Calculate the mass difference:

\(\displaystyle \Delta m = m_{\text{Rn}} – (m_{\text{Po}} + m_{\alpha}) \)

\(\displaystyle \Delta m = 222.017578 – (218.008973 + 4.002603) \)

\(\displaystyle \Delta m = 222.017578 – 222.011576 \)

\(\displaystyle \Delta m = 0.006002 \, \text{u} \)

Convert the mass difference to energy:

\(\displaystyle Q = 0.006002 \, \text{u} \times 931.5 \, \text{MeV/u} \)

\(\displaystyle Q \approx 5.59 \, \text{MeV} \)

The energy released in the alpha decay of Radon-222 is approximately 5.59 MeV.

Problem 5: If a Thorium-230 nucleus undergoes alpha decay, calculate the kinetic energy of the alpha particle and the recoil nucleus. The atomic masses are:

• (\(\displaystyle ^{230}_{90}\text{Th} \)): 230.033126 u
• (\(\displaystyle ^{226}_{88}\text{Ra} \)): 226.025403 u
• (\(\displaystyle ^{4}_{2}\text{He} \)): 4.002603 u

Solution: First, calculate the Q value of the decay:

\(\displaystyle Q = (m_{\text{Th}} – m_{\text{Ra}} – m_{\alpha}) \times 931.5 \, \text{MeV/u} \)

Given:

\(\displaystyle m_{\text{Th}} = 230.033126 \, \text{u} \)

\(\displaystyle m_{\text{Ra}} = 226.025403 \, \text{u} \)

\(\displaystyle m_{\alpha} = 4.002603 \, \text{u} \)

Calculate the mass difference:

\(\displaystyle \Delta m = 230.033126 – (226.025403 + 4.002603) \)

\(\displaystyle \Delta m = 230.033126 – 230.028006 \)

\(\displaystyle \Delta m = 0.005120 \, \text{u} \)

Convert the mass difference to energy:

\(\displaystyle Q = 0.005120 \, \text{u} \times 931.5 \, \text{MeV/u} \)

\(\displaystyle Q \approx 4.77 \, \text{MeV} \)

The kinetic energy of the alpha particle (\(\displaystyle K_{\alpha} \)) and the recoil nucleus (\(\displaystyle K_{\text{Ra}} \)) can be determined using the conservation of momentum and energy. Since the alpha particle and the recoil nucleus have equal and opposite momenta:

\(\displaystyle m_{\alpha} v_{\alpha} = m_{\text{Ra}} v_{\text{Ra}} \)

Using the relationship for kinetic energy:

\(\displaystyle K_{\alpha} = \frac{Q \cdot m_{\text{Ra}}}{m_{\alpha} + m_{\text{Ra}}} \)

\(\displaystyle K_{\text{Ra}} = \frac{Q \cdot m_{\alpha}}{m_{\alpha} + m_{\text{Ra}}} \)

Convert masses to kg:

\(\displaystyle m_{\alpha} = 4 \, \text{u} = 4 \times 1.66 \times 10^{-27} \, \text{kg} \)

\(\displaystyle m_{\text{Ra}} = 226 \, \text{u} = 226 \times 1.66 \times 10^{-27} \, \text{kg} \)

Calculate the kinetic energies:

\(\displaystyle K_{\alpha} = \frac{4.77 \times 226}{4 + 226} \)

\(\displaystyle K_{\alpha} = \frac{4.77 \times 226}{230} \)

\(\displaystyle K_{\alpha} \approx 4.69 \, \text{MeV} \)

\(\displaystyle K_{\text{Ra}} = \frac{4.77 \times 4}{230} \)

\(\displaystyle K_{\text{Ra}} \approx 0.08 \, \text{MeV} \)

The kinetic energy of the alpha particle is approximately 4.69 MeV, and the kinetic energy of the recoil Ra-226 nucleus is approximately 0.08 MeV.

FAQs