The concept of the angle of contact is deeply rooted in the study of surface tension and capillarity. It was first introduced by the English polymath Thomas Young in 1805. Young was interested in understanding the forces that govern the contact between different phases—solids, liquids, and gases.
Young’s work laid the foundation for the scientific understanding of how liquids interact with solid surfaces. He described the angle formed at the junction between a liquid and a solid surface, which we now refer to as the angle of contact. This angle helps us understand whether a liquid will spread out over a surface (wet it) or form droplets (not wet it).
Following Young’s initial description, other scientists, including Pierre-Simon Laplace, expanded on the concept. They explored how the angle of contact could be used to predict and explain various phenomena, such as the rise of water in a capillary tube or the shape of a droplet on a leaf.
Over the years, the angle of contact has become a crucial parameter in many scientific fields, including materials science, biology, and engineering. It helps researchers design surfaces with specific properties, like water-repellent coatings for fabrics or anti-fog treatments for glasses.
What is the Angle of Contact?
Definition: Angle of contact is defined as the angle between the tangent to the liquid surface and the solid surface inside the liquid at the point of contact.
When we talk about the angle of contact, we’re referring to a specific angle that tells us how a liquid is interacting with a solid surface. To visualize this, think about a drop of water on a lotus leaf. The edge where the water touches the leaf isn’t just a straight line; it curves up or down slightly. This curve forms an angle with the surface of the leaf, and that’s what we call the angle of contact.
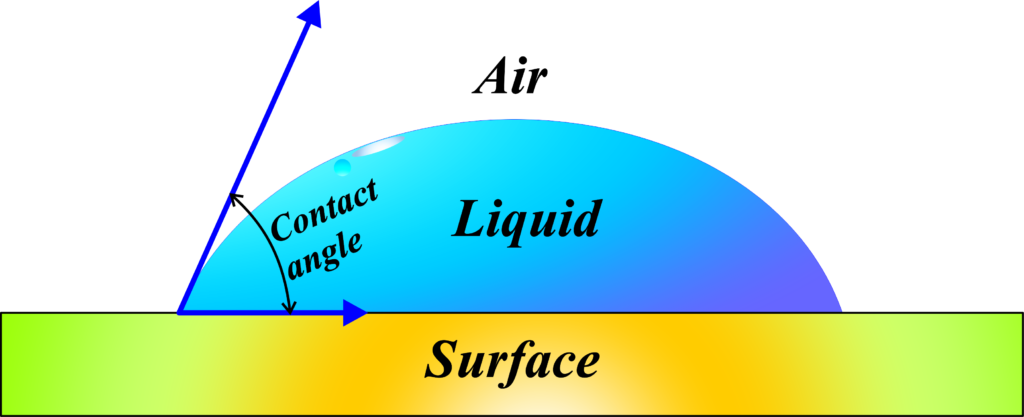
Mathematically, it’s the angle formed between a line tangent to the liquid surface at the point of contact and the solid surface itself, measured from inside the liquid. If you could shrink down and stand inside the drop of water, looking out towards the leaf, the angle of contact is the angle you’d measure from the leaf’s surface up to the line that just grazes the top of the water droplet.
This angle is super important because it tells us if the liquid likes to spread out over the solid (wetting) or if it prefers to stay bunched up in a droplet (non-wetting). A smaller angle means better wetting and a larger angle means the liquid is more likely to form droplets.
Imagine you’ve just washed your hands and you’re looking at a water droplet clinging to the tap. The shape of that droplet is determined by how the water interacts with the surface of the tap. At the point where the water droplet meets the tap, there’s a specific angle formed—this is what we call the angle of contact.
In more scientific terms, the angle of contact is the angle formed at the interface between a liquid and a solid surface. It’s measured from the solid surface through the liquid, to the tangent of the liquid’s surface at the point of contact. This angle tells us a lot about how the liquid behaves on that surface.
If the angle is small, less than 90 degrees, the liquid likes the surface and spreads out, which is called wetting. If the angle is large, greater than 90 degrees, the liquid doesn’t like the surface much and prefers to stay in a droplet, which is called non-wetting.
So, when you’re observing that water droplet, you’re seeing the angle of contact in action. It’s a simple concept that explains a lot about the interactions between liquids and solids, and it’s very important in understanding phenomena like water resistance or capillary action where liquids move up against gravity in thin tubes.
Wetting (Hydrophilic)
When a liquid spreads out on a solid surface, it’s called wetting. Surfaces that attract water are hydrophilic. If the angle of contact is less than 90°, it indicates good wetting.
When we say a surface is hydrophilic, we’re saying it’s a friend of water—it likes to get wet. “Hydro” means water, and “philic” means loving, so hydrophilic surfaces are water-loving surfaces.

Now, imagine you’re watering a plant, and some of the water spills onto the leaves. If the leaves are hydrophilic, the water will spread out and cover the surface in a thin layer. This happens because the molecules of the leaf surface are attracted to the water molecules more than the water molecules are attracted to each other. This attraction causes the water to “stick” to the leaf and spread out.
In terms of the angle of contact, on a hydrophilic surface, this angle is less than 90 degrees. The smaller the angle, the more the liquid wets the surface. So, if you see water spreading out flat and covering a large area, you’re looking at a hydrophilic surface in action.
Partial Wetting
Partial wetting describes the behavior of a liquid when it comes into contact with a solid surface, where the liquid forms a distinct droplet that neither spreads out completely nor beads up into a perfect sphere. Instead, the liquid droplet adopts an intermediate shape, forming a measurable contact angle with the surface.
Imagine you’re trying to paint a picture, and you dip your brush in watercolor. When you press the brush against the paper, the paint spreads out, but not completely—it doesn’t cover the entire surface of the paper. This is an example of partial wetting.
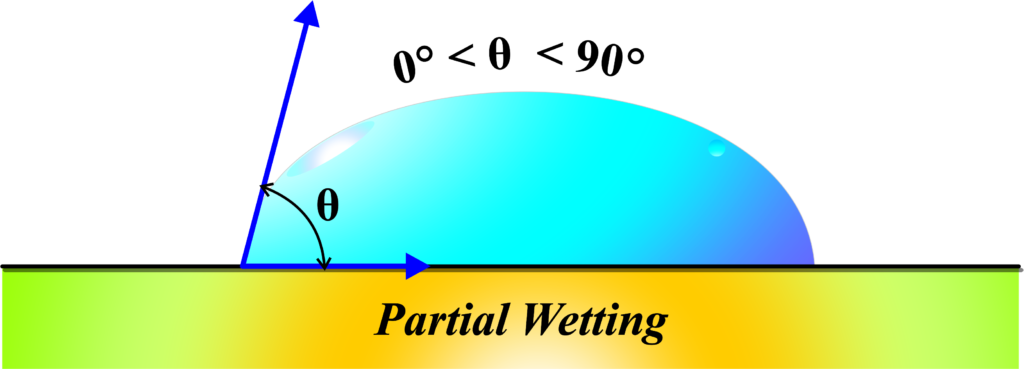
In physics, partial wetting refers to the situation where a liquid spreads out over a surface, but only to a certain extent. It doesn’t form a complete layer over the surface, nor does it stay as a compact droplet; it’s somewhere in between.
The angle of contact in partial wetting is between 0 and 90 degrees. This means the forces of cohesion (which make the liquid want to stay together in a droplet) and adhesion (which make the liquid want to spread out on the surface) are balanced. The liquid spreads out, but not completely, because while it’s attracted to the surface, it’s also trying to minimize its surface area due to surface tension.
This concept is important in many real-world applications. For example, when you’re writing with a pen, the ink partially wets the paper, which allows it to spread enough to be readable but not so much that it becomes a blot. Similarly, partial wetting is considered when designing products like waterproof coatings that need to repel water but not to the extent of being superhydrophobic.
Non-wetting (Hydrophobic)
Non-wetting surfaces repel water. These are hydrophobic. “Hydrophobic” is a term that comes from Greek, where “hydro” means water and “phobic” means fear. So, hydrophobic surfaces are those that are afraid of water, or more scientifically, they repel water.
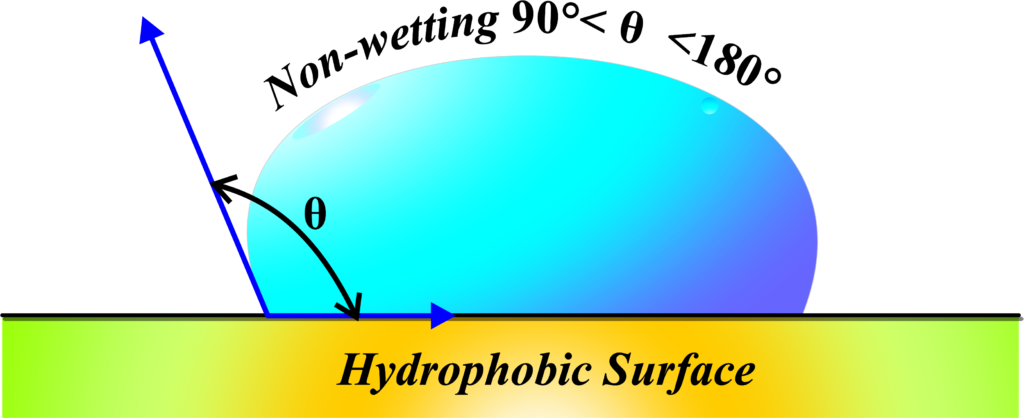
Imagine you’re wearing a raincoat during a downpour. The water droplets hit the surface but don’t spread out; instead, they form little beads and roll off. That’s because the material of the raincoat is hydrophobic—it doesn’t get wet easily.
In physics, when we talk about non-wetting surfaces, we’re referring to surfaces where the angle of contact—the angle between the surface and the edge of a water droplet—is greater than 90 degrees. If the angle of contact is greater than 90°, the liquid tends to form droplets instead of spreading. This large angle of contact means that the water droplet maintains its shape and doesn’t spread out across the surface.
Why does this happen? It’s all about the forces of attraction. On a hydrophobic surface, the attraction between the water molecules themselves (cohesion) is stronger than the attraction between the water molecules and the surface molecules (adhesion). This causes the water to pull itself into a shape with the least surface area, which is a droplet.
This concept is not just for raincoats. It’s used in many applications, like creating non-stick cookware, and waterproof paints, and even in nature—like the leaves of the lotus plant, which stay clean because dirt particles are picked up by water droplets and carried away due to the plant’s hydrophobic surface.
Liquid Repellent Surface (Superhydrophobic)
Superhydrophobic surfaces are extremely repellent to water, often having angles of contact greater than 150°. Water droplets bead up and roll off these surfaces.
Imagine walking in the rain with your favorite pair of waterproof shoes. The water droplets hit your shoes but instead of soaking in, they bead up and roll right off. This magic is thanks to a superhydrophobic surface on your shoes.

“Superhydrophobic” surfaces are the superheroes of materials when it comes to repelling water. The term combines “super,” meaning above or beyond, with “hydrophobic,” which we learned means water-fearing. So, superhydrophobic surfaces are extremely good at repelling water.
But how do they do it? These surfaces have special structures, often too small to see with the naked eye, that trap air in tiny grooves or bumps. When a water droplet lands on this kind of surface, it barely touches the solid material; it’s mostly sitting on a cushion of air. This means there’s very little friction, so the water droplet can easily roll away.
In physics terms, a superhydrophobic surface has an angle of contact that’s usually greater than 150 degrees. This high angle means that water droplets make minimal contact with the surface and tend to keep their spherical shape, allowing them to roll off quickly.
One cool example of a superhydrophobic material is black silicon, which has been studied for its unique ability to repel water by riding on a thin air-film gap trapped beneath the droplets. This property is cool to watch and has practical applications, like making transportation systems more aerodynamic or medical devices more sterile.
So, when we talk about liquid-repellent surfaces, we discuss materials designed to keep water away as efficiently as possible.
Given table outlines the key differences between hydrophilic wetting, partial wetting, hydrophobic non-wetting, and superhydrophobic liquid-repellent surfaces.
| Behavior | Wetting (Hydrophilic) | Partial Wetting | Non-wetting (Hydrophobic) | Liquid Repellent (Superhydrophobic) |
|---|---|---|---|---|
| Angle of Contact | Less than 90° | Between 0° and 90° | Greater than 90° | Greater than 150° |
| Surface Affinity | High affinity for water; liquid spreads out | Moderate affinity; liquid spreads but not completely | Low affinity; liquid forms droplets | Extremely low affinity; liquid forms spherical droplets |
| Surface Energy | Low; liquid prefers to maximize contact with the surface | Balanced; liquid partially spreads to minimize energy | High; liquid minimizes contact with the surface | Very high; liquid barely touches the surface |
| Example | Water on clean glass | Watercolor paint on paper | Water on waxed car surface | Water on a waxed car surface |
| Application | Coatings that enhance liquid spread, like on smartphone screens | Materials that need to absorb liquids but not too quickly, like paper towels | Waterproof clothing and materials | Self-cleaning surfaces and anti-stain fabrics |
Characteristics of the Angle of Contact
The angle of contact tells us about the liquid’s wetting ability on a surface. It’s influenced by the intermolecular forces between the liquid and solid, and it’s a key factor in adhesion and cohesion. Here are some key points:
- Consistency: The angle of contact is consistent for a particular liquid-solid pair. This means if you take the same liquid and solid under the same conditions, the angle of contact will be the same every time you measure it.
- Dependence on Materials: The value of the angle of contact depends on the nature of the liquid and the solid in contact. Different materials have different levels of attraction to each other, which affects the angle.
- Influence of the Surrounding Medium: The medium above the liquid’s free surface can influence the angle of contact. For example, the angle of contact of water in air might be different from that of water in an oil environment.
- Sensitivity to Conditions: Factors like impurities or temperature changes can alter the angle of contact. Adding something to the liquid or changing its temperature can make the liquid more or less willing to spread out on the solid surface.
- Wetting and Non-wetting: If the angle of contact is less than 90 degrees, it indicates good wetting, meaning the liquid spreads out on the solid. If it’s greater than 90 degrees, it indicates non-wetting, where the liquid forms droplets instead of spreading.
- Partial Wetting: Sometimes, the angle of contact is between 0 and 90 degrees, indicating partial wetting. The liquid spreads out but not completely.
Cohesion
Cohesion is all about the attraction between similar molecules that keeps them together, creating the unique properties of substances, particularly liquids like water. It plays a role in the formation of droplets and the angle of contact.
Cohesion is like the “team spirit” of molecules. It’s the force that keeps molecules of the same substance sticking together. Just like a group of friends holding hands, cohesion is what happens when molecules are so attracted to each other that they stay close, forming a united group.
- Cohesive Forces: These are the invisible “hands” that hold molecules together. They’re especially strong in liquids and solids, where molecules are close to each other.
- Surface Tension: Thanks to cohesion, liquids have something called surface tension. It’s like a skin on the surface of water that can hold up light objects, such as a paperclip or a water strider insect.
- Cohesive Energy: This is the “strength” of the team spirit. The more energy it takes to pull molecules apart, the stronger the cohesion.
Example: When you see a drop of water on a leaf, it’s cohesion that keeps the water together in a droplet shape instead of spreading out.
Cohesion isn’t just a cool science fact; it’s essential for many natural processes, like how water travels from the roots to the leaves in plants, and it’s also crucial in many technologies we use every day.
Adhesion
Adhesion is the force between molecules of different substances, like water and glass. It competes with cohesion and affects the angle of contact.
Adhesion is like the friendship between different kinds of molecules. It’s the force that makes molecules of different substances stick to each other. Just as you might hold hands with a friend, adhesion is what happens when, for example, water molecules stick to the molecules of a glass surface.
- Adhesive Forces: These are the forces that cause different substances to come together. They can be due to various factors, including electrostatic forces or the physical interlocking of molecular structures.
- Examples of Adhesion: When you spill water on a table, it sticks to the surface instead of just forming a ball and rolling off. That’s adhesion in action. Another example is when paint adheres to a wall.
- Adhesion vs. Cohesion: While cohesion is the force within the same substance, adhesion is the attraction between different substances. For instance, cohesion keeps water droplets together, but adhesion makes those droplets stick to a window pane.
Adhesion is crucial for many processes in nature and technology. It’s why bandages stick to our skin, and why ink sticks to paper, and it plays a role in biological systems, like how plant roots take up water from the soil.
So, adhesion is all about the attraction between different materials, and it’s a key concept in understanding how substances interact with each other in both everyday life and scientific applications.
Meniscus Effect
The meniscus is the curve seen at the top of a liquid in response to its container. A concave meniscus occurs when the liquid wets the container (angle of contact less than 90°), and a convex meniscus occurs when it doesn’t (angle of contact greater than 90°).
When you pour water into a glass, you might notice that the surface of the water isn’t flat. Instead, it curves near the edges of the glass. This curve is called the meniscus, and it’s a result of the water’s surface tension interacting with the container.
Surface Tension: Water molecules are attracted to each other, pulling themselves together to create the smallest surface area possible. This force is called surface tension. This is like an invisible skin on the surface of liquids. It happens because the molecules at the surface are attracted to each other and to the molecules of the container. They’re trying to hold onto each other as tightly as possible, creating tension.
Adhesion and Cohesion: Adhesion is the attraction between water molecules and the molecules of the container. Cohesion is the attraction between water molecules themselves.
- Adhesion: This is the force that causes different substances to stick together. In our glass of water, adhesion is what makes the water molecules stick to the glass walls. Because of adhesion, the water climbs up the sides of the glass slightly, creating a curved edge.
- Cohesion: This is the force that holds similar substances together. For water, cohesion is the attraction between water molecules. It’s what gives water its droplet shape and surface tension. Inside the glass, cohesion pulls the water molecules toward each other, away from the glass.
Concave or Convex: Because of surface tension, the surface of the liquid will curve. If the liquid likes the container (like water in a glass), it will try to maximize contact, creating a concave meniscus. If the liquid doesn’t like the container (like mercury in a glass), it will minimize contact, creating a convex meniscus. If adhesion is stronger than cohesion (like water in a glass), the meniscus curves downward, creating a concave shape. If cohesion is stronger (like mercury in a glass), the meniscus curves upward, forming a convex shape.
Convex Meniscus
When you look at mercury in a glass container, you’ll notice that it forms a dome-like shape at the edges. This dome is what we call a convex meniscus. Unlike water, which forms a concave meniscus and curves down, mercury curves up because of its unique properties.

- Strong Cohesion: Mercury atoms are highly attracted to each other, much more than they are attracted to the glass. This strong cohesive force pulls the mercury atoms together, creating a bulge instead of spreading out.
- Weak Adhesion: The adhesion, or the attraction between mercury atoms and the glass, is relatively weak. So, the mercury doesn’t climb up the walls of the container as water does.
- Surface Tension: The surface tension of mercury tries to minimize the surface area of the liquid. Since the cohesive forces are dominant, the smallest surface area for mercury is a curved, convex shape.
The angle of Contact: The angle of contact for mercury on glass is greater than 90 degrees, typically around 140 degrees. This angle is measured from the tangent of the mercury at the point of contact with the glass, inside the mercury.
Understanding the convex meniscus in mercury is important for several reasons: It explains why mercury is used in old-fashioned thermometers; the convex meniscus makes it easy to read the level of mercury. It’s a clear demonstration of the balance between cohesive and adhesive forces in liquids.
So, we can say that, a convex meniscus in mercury is a result of the liquid’s strong cohesion and weak adhesion with the container, leading to a characteristic dome-shaped curve and an angle of contact typically greater than 90 degrees.
Flat Meniscus
A flat meniscus represents a unique state where the forces of adhesion and cohesion are in perfect equilibrium, resulting in a liquid surface that is level and an angle of contact that is 90 degrees. A flat meniscus is a bit of a special case when it comes to liquids in containers. Unlike the more common concave or convex meniscus, a flat meniscus occurs when the adhesive and cohesive forces are balanced in such a way that the surface of the liquid is flat across the top.
- Adhesive Forces: These are the forces that cause the liquid to stick to the container. In water, for example, adhesive forces make it climb up the sides of a glass slightly.
- Cohesive Forces: These are the forces that cause the liquid molecules to stick to each other. They pull the center of the liquid’s surface up, trying to minimize the surface area.
When these two forces are perfectly balanced, the liquid doesn’t climb up the sides or dip in the middle. Instead, it forms a flat surface.
Example: Pure water in contact with clean silver can create a flat meniscus. This is because the adhesive forces between the water and silver are equal to the cohesive forces within the water molecules.
The angle of Contact: For a flat meniscus, the angle of contact is exactly 90 degrees. This means that the tangent at the point of contact with the container forms a right angle with the container wall.
Understanding the flat meniscus is important because it’s an indicator of a very balanced interaction between a liquid and a container. It’s less common than the other types of meniscus but can be seen in certain laboratory conditions or with specific liquid-metal combinations.
Concave Meniscus
A concave meniscus occurs when the surface of a liquid curves downwards at the edges where it touches the walls of a container. This is the most common type of meniscus observed with liquids like water.
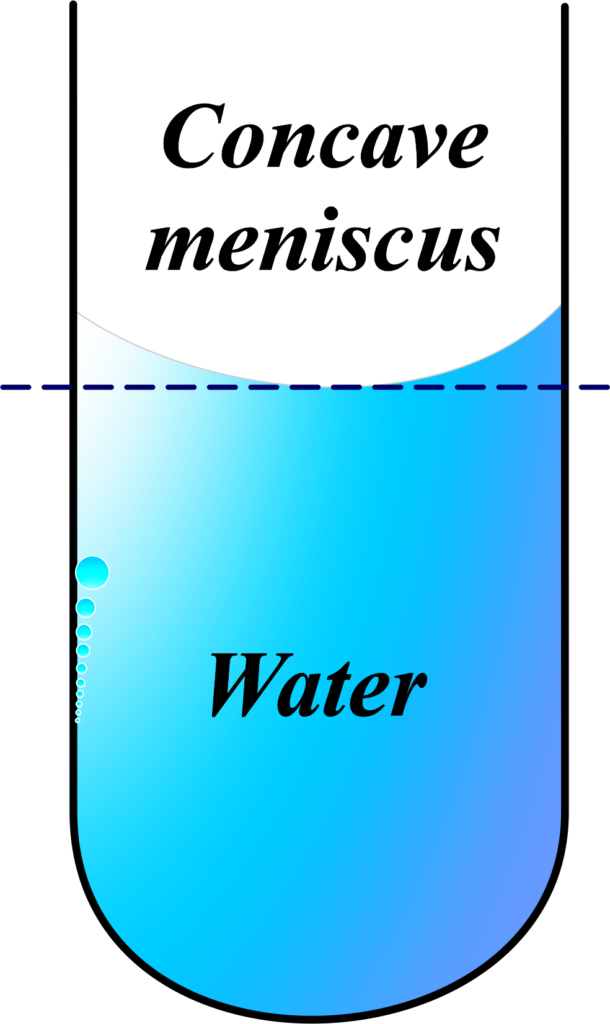
- Adhesion Over Cohesion: The concave shape forms because the adhesive forces between the liquid molecules and the container’s walls are stronger than the cohesive forces between the liquid molecules themselves. This causes the liquid to climb up the sides of the container, creating a dip in the middle¹.
- Surface Tension: The liquid’s surface tension pulls the liquid up along the container’s walls, while gravity pulls the bulk of the liquid down, resulting in the curved shape.
Example: When you fill a glass with water, you’ll notice the water level is higher at the edges than in the middle. That’s a concave meniscus.
The angle of Contact: For a concave meniscus, the angle of contact is less than 90 degrees. It’s measured from the tangent at the point of contact with the container, inside the liquid.
When reading the volume of a liquid in a graduated cylinder, you should always read from the bottom of the concave meniscus at eye level. This ensures precision in laboratory work and helps students grasp the practical applications of the concepts of adhesion, cohesion, and surface tension.
The meniscus effect is important because it shows us how liquids behave in different containers and helps us measure the volume of liquids accurately.
Deriving the Angle of Contact Formula Using the Meniscus Effect
The angle of contact, also known as the contact angle, is the angle at which a liquid interface meets a solid surface. It’s important to understand how liquids interact with surfaces. L
When water is placed in a capillary tube, the adhesive forces between the water molecules and the tube are stronger than the cohesive forces among the water molecules. This causes the water to rise in the tube, forming a concave meniscus.
The angle of contact (θ) is the angle formed between the tangent to the liquid surface at the point of contact and the solid surface.
Weight of Liquid Raised: The weight of the liquid column raised in the tube can be calculated using the volume of the liquid and its specific weight.
The volume of the liquid column \(\displaystyle = \text{cross-sectional area of the tube} \times \text{height of the liquid column} \).
For a capillary tube with diameter (d) and height (h):
\(\displaystyle\text{Weight of the liquid raised} = \left( \frac{\pi d^2}{4} \right) h w \)
where (w) is the specific weight of the liquid.
Vertical Component of Surface Tension Force: Surface tension (σ) acts along the circumference of the meniscus, creating a force component in the vertical direction. The vertical component of the surface tension force is given by:
\(\displaystyle F_{\text{vertical}} = \sigma \cos \theta \times \text{circumference of the tube} \)
The circumference of the tube is \(\displaystyle \pi d \):
\(\displaystyle F_{\text{vertical}} = \sigma \cos \theta \times \pi d \)
At equilibrium, the vertical component of the surface tension force balances the weight of the liquid column raised:
\(\displaystyle \sigma \cos \theta \times \pi d = \left( \frac{\pi d^2}{4} \right) h w \)
Simplify the equation to solve for (cos θ):
\(\displaystyle \sigma \cos \theta \times \pi d = \frac{\pi d^2}{4} h w \)
\(\displaystyle \sigma \cos \theta = \frac{h w d}{4} \)
\(\displaystyle \cos \theta = \frac{h w d}{4 \sigma} \)
Finally, solve for (θ):
\(\displaystyle \theta = \cos^{-1} \left( \frac{h w d}{4 \sigma} \right) \)
Contact Angle (θ): This angle determines the shape of the meniscus:
- If \(\displaystyle( 0 \leq \theta < 90^\circ \)), the meniscus is concave, indicating strong adhesive forces.
- If \(\displaystyle( 90^\circ \leq \theta < 180^\circ \)), the meniscus is convex, indicating weaker adhesive forces relative to cohesive forces.
Zero Contact Angle: When the contact angle is zero, the tangent to the surface tension force is collinear or parallel with the side surface of the capillary tube, indicating complete wetting of the surface.
Also Read: Surface Energy
Significance of the Angle of Contact
The angle of contact is significant in many applications, from designing water-repellent materials to understanding biological systems. It’s a crucial parameter in the study of fluid dynamics and material science.
- Determines Wetting Behavior: The angle of contact tells us if a liquid will spread out over a surface (wet it) or form droplets (not wet it). A smaller angle means better wetting, which is crucial for processes like painting or inkjet printing.
- Influences Capillary Action: This angle helps predict capillary action, which is how water moves up in a thin tube against gravity. It’s essential for understanding how plants draw water from their roots to their leaves.
- Affects Adhesion and Cohesion: The angle of contact shows the balance between adhesion (liquid sticking to the solid) and cohesion (liquid sticking to itself). This balance is vital in the design of adhesive products and waterproof coatings.
- Guides Material Design: Knowing the angle of contact helps scientists and engineers create materials with specific properties, like water-repellent surfaces or adhesives that work in wet conditions.
- Surface Tension Insights: It provides insights into the surface tension of liquids, which is important for sizing droplets in sprays and understanding the behavior of liquids in different environments.
So, the angle of contact is a fundamental concept that has significant implications in both natural phenomena and various technological applications.
Solved Examples
Example 1: A drop of water on a glass surface forms an angle of contact of (30∘), while the same water on a wax surface forms an angle of (120∘). Explain the difference in wetting behavior on these surfaces.
Solution: The angle of contact (θ) is determined by the balance between cohesive forces (within the liquid) and adhesive forces (between the liquid and solid surface).
Water on Glass (30∘): This small angle of contact indicates strong adhesive forces between water and glass, meaning the water wets the surface well (hydrophilic behavior).
Water on Wax (120∘): This large angle of contact indicates weak adhesive forces between water and wax, meaning the water does not wet the surface well (hydrophobic behavior).
Thus, the wetting behavior varies due to the different adhesive forces between water and the surfaces of glass (hydrophilic) and wax (hydrophobic).
Example 2: Describe and calculate the shape and height of the meniscus formed when a capillary tube with an internal radius of 0.5 mm is dipped in mercury (surface tension = 0.465 N/m, contact angle = 140°, density = 13500 kg/m³.
Solution:
- Shape of Meniscus: Mercury forms a convex meniscus due to its contact angle being greater than (90°).
- Height of Meniscus Depression:
- Surface tension (σ) = 0.465 N/m
- Contact angle (θ) = 140° (cos 140°c = -0.766)
- Density (ρ) = 13500 kg/m³
- Radius (r) = 0.5 mm = 0.0005 m
- Acceleration due to gravity (g) = 9.8 m/s²
The height of depression (h) is given by:
\(\displaystyle h = \frac{2\sigma \cos \theta}{\rho g r} \)
Substituting the values:
\(\displaystyle h = \frac{2 \times 0.465 \times (-0.766)}{13500 \times 9.8 \times 0.0005} \)
\(\displaystyle h = \frac{-0.71214}{6.615} \)
\(\displaystyle h \approx -0.1076 \, \text{m} \)
The negative sign indicates a depression. Therefore, the mercury meniscus is depressed by approximately 10.76 cm.
Example 3: A soap bubble with an initial radius of 1 cm is blown to a final radius of 3 cm. Calculate the work done, given the surface tension of the soap solution is 0.03 N/m.
Solution: For a soap bubble, there are two surfaces contributing to the surface energy.
Initial surface area (A1):
\(\displaystyle A_1 = 2 \times 4\pi r_1^2 = 8\pi r_1^2 \)
\(\displaystyle A_1 = 8\pi (0.01)^2 \)
\(\displaystyle A_1 = 0.0008\pi \, \text{m}^2 \)
Final surface area (A2):
\(\displaystyle A_2 = 2 \times 4\pi r_2^2 = 8\pi r_2^2 \)
\(\displaystyle A_2 = 8\pi (0.03)^2 \)
\(\displaystyle A_2 = 0.0072\pi \, \text{m}^2 \)
Change in surface area (∆A):
\(\displaystyle \Delta A = A_2 – A_1 = 0.0072\pi – 0.0008\pi \)
\(\displaystyle \Delta A = 0.0064\pi \, \text{m}^2 \)
Work done (W) is given by:
\(\displaystyle W = \sigma \cdot \Delta A \)
\(\displaystyle W = 0.03 \times 0.0064\pi \)
\(\displaystyle W = 0.000192\pi \, \text{J} \)
\(\displaystyle W \approx 0.0006 \, \text{J} \)
So, the work done in expanding the soap bubble is approximately (0.0006 J).
Example 4: Calculate the height to which mercury (with surface tension (0.486 N/m) and specific weight (133000 N/m3) rises in a capillary tube of diameter 1 mm if the contact angle is ( 130∘).
Solution:
- Diameter, ( d = 1 mm = 0.001 m)
- Surface tension of mercury, (σ = 0.486 N/m)
- Specific weight of mercury, ( w = 133000 N/m3)
- Contact angle, (θ = 130∘)
Using the formula rearranged to solve for height (h):
\(\displaystyle \cos \theta = \frac{hwd}{4\sigma}\)
\(\displaystyle h = \frac{4\sigma \cos \theta}{wd}\)
Substitute the known values:
\(\displaystyle \cos 130^\circ = -0.6428\)
\(\displaystyle h = \frac{4 \times 0.486 \times (-0.6428)}{133000 \times 0.001}\)
Calculate the numerator and denominator:
\(\displaystyle \text{Numerator} = 4 \times 0.486 \times (-0.6428) = -1.248\)
\(\displaystyle \text{Denominator} = 133000 \times 0.001 = 133\)
Divide to find the height:
\(\displaystyle h = \frac{-1.248}{133} \approx -0.00938 \, \text{m} \approx -9.38 \, \text{mm}\)
A negative value for height indicates mercury depresses rather than rises, consistent with its cohesive properties.
Example 5: Given a liquid rises to a height of 3 cm in a capillary tube of diameter 0.5 mm and has a contact angle of ( 60∘). The surface tension of the liquid is ( 0.03 N/m). Calculate the specific weight of the liquid.
Solution:
- Height, ( h = 3 cm = 0.03m)
- Diameter, ( d = 0.5 mm= 0.0005 m)
- Contact angle, (θ= 60∘)
- Surface tension, (σ = 0.03 N/m)
Using the formula rearranged to solve for specific weight (w):
\(\displaystyle \cos \theta = \frac{hwd}{4\sigma}\)
\(\displaystyle w = \frac{4\sigma \cos \theta}{hd}\)
Substitute the known values:
\(\displaystyle \cos 60^\circ = 0.5\)
\(\displaystyle w = \frac{4 \times 0.03 \times 0.5}{0.03 \times 0.0005}\)
Calculate the numerator and denominator:
\(\displaystyle \text{Numerator} = 4 \times 0.03 \times 0.5 = 0.06\)
\(\displaystyle \text{Denominator} = 0.03 \times 0.0005 = 0.000015\)
Divide to find the specific weight:
$latex \displaystyle w = \frac{0.06}{0.000015} = 4000 \, \text{N/m}^3
FAQs
What is the angle of contact, and how is it measured in fluid systems?
The angle of contact, or contact angle, is the angle formed between the tangent to the liquid surface at the point of contact and the solid surface. It is measured using a goniometer by observing a droplet of liquid on a solid surface. The contact angle indicates the wettability of the surface: a smaller angle means better wetting (hydrophilic surface), while a larger angle means poorer wetting (hydrophobic surface).
How does the meniscus effect occur, and what factors influence its shape?
The meniscus effect occurs due to the adhesive forces between the liquid and the container wall and the cohesive forces within the liquid. If adhesive forces are stronger, the liquid climbs up the walls, creating a concave meniscus (as seen with water in glass). If cohesive forces are stronger, the liquid curves downward, creating a convex meniscus (as seen with mercury in glass). The shape of the meniscus is influenced by the balance between adhesive and cohesive forces.
What is meant by wetting, and how is a hydrophilic surface characterized?
Wetting refers to the ability of a liquid to maintain contact with a solid surface. A hydrophilic surface is one that has a strong attraction to water, characterized by a contact angle less than 90 degrees. This results in the liquid spreading out on the surface, indicating good wetting properties. Such surfaces are common in applications where water spreading or absorption is desired, such as in paper towels or sponges.
What is partial wetting, and how does it differ from complete wetting and non-wetting?
Partial wetting occurs when the contact angle is between 0 and 90 degrees, indicating that the liquid spreads somewhat but not completely over the surface. In complete wetting (contact angle of 0 degrees), the liquid spreads out entirely, covering the surface uniformly. Non-wetting, or hydrophobic behavior, occurs when the contact angle is greater than 90 degrees, causing the liquid to form droplets and not spread out, as seen in water on a waxed car surface.
What are the characteristics of a superhydrophobic surface, and how is it created?
A superhydrophobic surface is extremely repellent to water, characterized by contact angles greater than 150 degrees and very low contact angle hysteresis. This causes water droplets to bead up and roll off the surface easily. Superhydrophobic surfaces are created by combining surface roughness with low surface energy materials, often using micro- and nanoscale structures and coatings like fluorinated compounds or silica nanoparticles.
How do cohesion and adhesion differ, and what roles do they play in fluid behavior on surfaces?
Cohesion refers to the attractive forces between molecules of the same substance, such as water molecules sticking together. Adhesion refers to the attractive forces between molecules of different substances, such as water molecules sticking to a glass surface. Cohesion contributes to the formation of droplets, while adhesion influences wetting and the interaction of liquids with solid surfaces. The balance between these forces determines phenomena like meniscus formation and capillary action.
What are some practical applications of understanding and manipulating surface wettability in everyday life and technology?
Understanding surface wettability has numerous applications. In everyday life, it influences the effectiveness of cleaning products, waterproof clothing, and water-repellent coatings for vehicles. In technology, it plays a critical role in inkjet printing, microfluidic devices, and biomedical applications such as anti-fouling surfaces and targeted drug delivery. Additionally, it is essential in industries like agriculture (for efficient irrigation) and electronics (to protect components from moisture).
