The history of speed and velocity in physics is a fascinating journey that intertwines with the development of calculus and the study of motion. Speed as a concept has been around since ancient times, as people have always been interested in how fast things move.
However, it was Galileo Galilei, an Italian physicist, who is often credited with being the first to measure speed scientifically. He defined speed as the distance covered per unit of time.
Velocity took a bit longer to be defined because it involves both speed and direction, making it a vector quantity. The development of the concept of velocity is closely linked to the work of Isaac Newton. Newton invented differential calculus, which allowed for the calculation of instantaneous velocity – the velocity of an object at a specific moment in time.
Speed
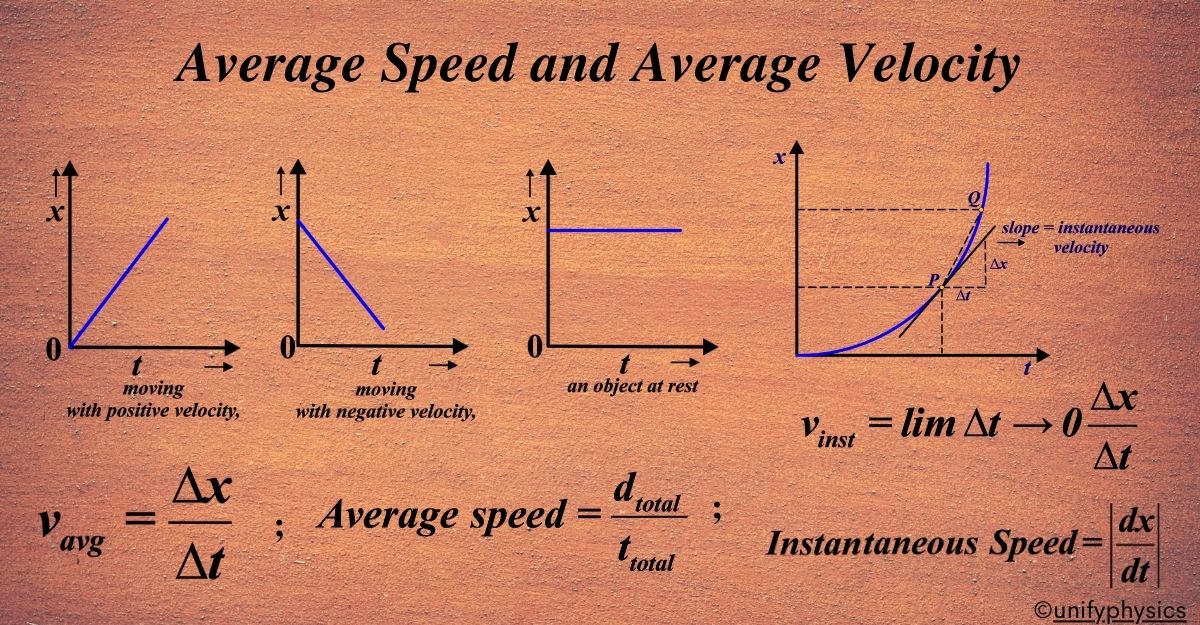
Speed is the rate at which an object covers distance. Speed is a measure of how quickly an object is moving. It’s calculated by dividing the distance traveled by the time it takes to travel that distance. The key point to remember is that speed does not have a direction associated with it; it’s a scalar quantity. This means that speed only tells us how fast an object is moving, not where it’s going. Here’s the formula for speed ((v)):
\(\displaystyle v = \frac{d}{t} \)
where: (v) is the speed, (d) is the distance traveled, (t) is the time taken. The standard unit of speed is meters per second (m/s) in the International System of Units (SI).
Example: Imagine a runner on a track. If the runner completes a 400-meter lap in 50 seconds, their speed is calculated as:
\(\displaystyle v = \frac{400 \text{ m}}{50 \text{ s}} = 8 \text{ m/s} \)
This tells us that the runner’s speed is 8 meters per second. However, it doesn’t tell us anything about the runner’s direction of travel. Whether they’re running straight, in circles, or zigzagging, the speed remains the same as long as the distance and time are consistent.
Velocity
Velocity is a fundamental concept in physics that describes the motion of an object with both magnitude and direction. It’s a vector quantity, which means it tells us not just how fast an object is moving, but also the direction in which it’s moving.
In more technical terms, velocity is defined as the rate of change of an object’s position with respect to time. It takes into account the object’s displacement, which is the straight-line distance from its starting point to its final position, along with the direction of that line. The formula for velocity (\(\displaystyle\vec{v}\)) is:
\(\displaystyle \vec{v} = \frac{\Delta \vec{x}}{\Delta t} \)
- \(\displaystyle\vec{v}\) is the velocity,
- \(\displaystyle\Delta \vec{x}\) is the displacement (change in position),
- (∆ t) is the time interval over which the displacement occurs.
Since velocity includes direction, it can be positive or negative based on the chosen frame of reference. For instance, if we consider the positive direction to be eastward, then an object moving east has a positive velocity, while an object moving west has a negative velocity.
Average Velocity
Average velocity is a vector quantity that represents the overall change in position, or displacement, of an object divided by the total time taken to make that change. It’s different from average speed, which is a scalar quantity and only considers the total distance traveled without regard to direction.
To understand average velocity, consider it as the velocity that would be required to go directly from the starting position to the ending position in a straight line over the same time interval that the actual motion took place. If a car travels 100 meters east, then 100 meters west in 10 seconds, its average velocity is 0 because the total displacement is zero. Here’s the formula for average velocity (\(\displaystyle\vec{v}_{avg}\)):
\(\displaystyle \vec{v}_{avg} = \frac{\Delta \vec{x}}{\Delta t} \)
- \(\displaystyle\vec{v}_{avg}\) is the average velocity,
- \(\displaystyle\Delta \vec{x}\) is the displacement (the straight-line distance from the initial to the final position),
- (∆t) is the total time taken.
If the direction of motion changes during the time interval, the average velocity may not give a complete picture of the object’s motion, but it does provide a useful measure of the overall rate of change of position.

The average velocity can be positive or negative depending upon the sign of the displacement. Students need to remember that since average velocity is a vector, it must include direction, and it can be zero even if the object has moved a considerable distance – if the object returns to its starting point, the displacement is zero, and so is the average velocity.
Also Read: Position, Path Length And Displacement
Average Speed
Average speed is a concept that quantifies the overall rate at which an object moves over a certain time, regardless of its direction of travel. It’s calculated by dividing the total distance traveled by the total time taken to travel that distance. Here’s the formula for average speed (vavg):
\(\displaystyle v_{avg} = \frac{d_{total}}{t_{total}} \)
- (vavg) is the average speed,
- (dtotal) is the total distance traveled,
- (ttotal) is the total time taken.
Unlike velocity, average speed doesn’t consider the direction of travel; it’s purely a measure of how fast an object moves. If an object takes a long, winding path, the average speed will consider the entire length of that path, not just the direct distance from start to finish.
Instantaneous Velocity
Instantaneous velocity is the velocity of an object at a specific moment in time. It’s the slope of the tangent to the position-time graph at any point. As point Q gets closer and closer to point P on the graph in Figure, the slope of the line PQ becomes the same as the slope of the curve at point P.
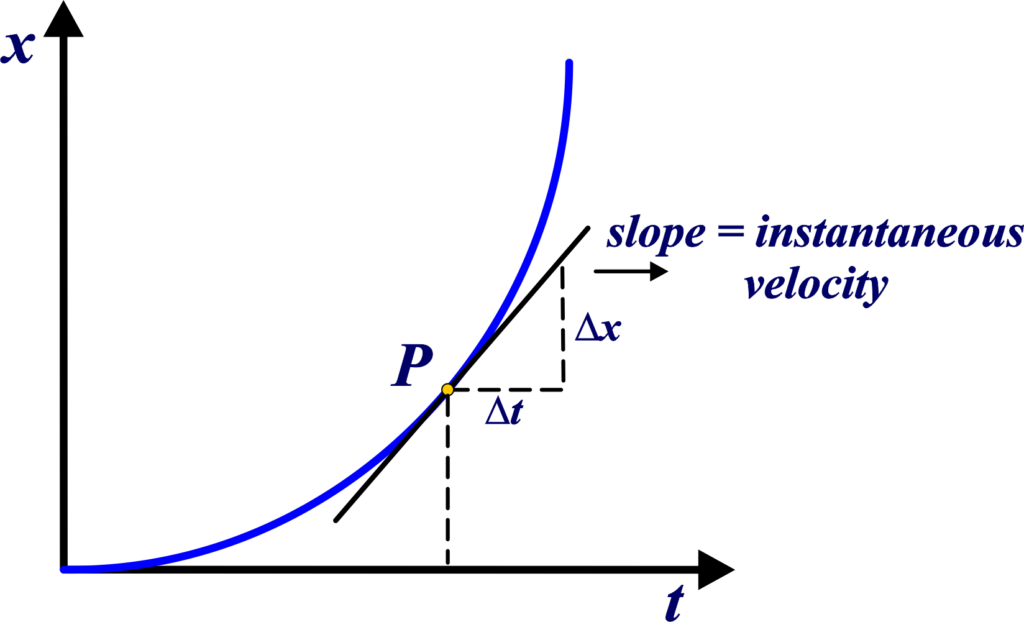
This means that at any point on the graph, the instantaneous velocity is equal to the slope of the tangent line touching the graph at that point. So, to find the instantaneous velocity, we can calculate the slope of the position-time graph, also known as the x-t graph.
Unlike average velocity, which tells us the overall rate of change of position over some time, instantaneous velocity gives us the speed and direction of an object at a particular instant. To find this, we use the concept of a limit to examine the velocity over an increasingly small time interval until it approaches zero. Here’s how we can express instantaneous velocity using the limit formula:
\(\displaystyle \vec{v}_{inst} = \lim{\Delta t \to 0} \frac{\Delta \vec{x}}{\Delta t} \)
The limit tells us what the average velocity \(\displaystyle\frac{\Delta \vec{x}}{\Delta t}\) becomes as the time interval (∆t) gets infinitesimally small. In other words, as the time interval approaches zero, the average velocity over that interval becomes the instantaneous velocity.
This is important because it allows us to calculate the exact velocity at any given moment, which is crucial for understanding the dynamics of moving objects. It’s a concept that’s central to calculus and is used extensively in physics to analyze motion.
Instantaneous Speed
Instantaneous speed is the speed of an object at a particular moment in time. It’s the magnitude of the instantaneous velocity, which means it tells us how fast the object is moving right then, without considering the direction.
Imagine you’re watching a car race. The speedometer of each car shows the instantaneous speed – it changes from moment to moment as the car speeds up, slows down, or maintains a steady pace. It’s a real-time measure of the car’s motion.
Mathematically, instantaneous speed is the absolute value of the derivative of the position with respect to time. It’s what you get when you calculate the average speed limit as the time interval approaches zero. In formula form, it looks like this:
\(\displaystyle \text{Instantaneous Speed} = \left| \frac{d\vec{x}}{dt} \right| \)
For students, understanding instantaneous speed is crucial for analyzing situations where the speed is not constant, such as a car accelerating down a highway or a ball being thrown up into the air. It’s a snapshot of an object’s motion at any given instant.
Solved Examples
Problem 1: A person walks 3 km at a speed of 6 km/h and then runs 2 km at a speed of 10 km/h. What is the average speed for the entire journey?
Solution: Time taken to walk 3 km:
\(\displaystyle t_1 = \frac{3 \text{ km}}{6 \text{ km/h}} = 0.5 \text{ hours} \)
Time taken to run 2 km:
\(\displaystyle t_2 = \frac{2 \text{ km}}{10 \text{ km/h}} = 0.2 \text{ hours} \)
Total distance traveled:
\(\displaystyle \text{Total Distance} = 3 \text{ km} + 2 \text{ km} = 5 \text{ km} \)
Total time taken:
\(\displaystyle \text{Total Time} = t_1 + t_2 = 0.5 \text{ hours} + 0.2 \text{ hours} = 0.7 \text{ hours} \)
Average speed is given by:
\(\displaystyle \text{Average Speed} = \frac{\text{Total Distance}}{\text{Total Time}} = \frac{5 \text{ km}}{0.7 \text{ hours}} \approx 7.14 \text{ km/h} \)
The average speed for the entire journey is approximately 7.14 km/h.
Problem 2: A car travels 80 km east in 2 hours, stops for 1 hour, then travels 60 km west in 1.5 hours. What is the average velocity of the car for the entire trip?
Solution: Total displacement:
\(\displaystyle \text{Displacement} = 80 \text{ km} \text{ east} – 60 \text{ km} \text{ west} = 20 \text{ km} \text{ east} \)
Total time taken:
\(\displaystyle \text{Total Time} = 2 \text{ hours} + 1 \text{ hour} + 1.5 \text{ hours} = 4.5 \text{ hours} \)
Average velocity is given by:
\(\displaystyle \text{Average Velocity} = \frac{\text{Displacement}}{\text{Total Time}} = \frac{20 \text{ km}}{4.5 \text{ hours}} \approx 4.44 \text{ km/h} \text{ east} \)
The average velocity of the car for the entire trip is approximately 4.44 km/h east.
Problem 3: A car’s velocity at (t = 2) seconds is given by the function (v(t) = 3t2 + 2t ). What is the instantaneous velocity of the car at (t = 2) seconds?
Solution: To find the instantaneous velocity at ( t = 2 ) seconds, we substitute ( t = 2 ) into the velocity function:
\(\displaystyle v(2) = 3(2)^2 + 2(2) = 3(4) + 4 = 12 + 4 = 16 \text{ m/s} \)
The instantaneous velocity of the car at ( t = 2 ) seconds is 16 m/s.
Problem 4: A sprinter runs 100 meters in 10 seconds. What is the sprinter’s average speed and instantaneous speed at 5 seconds, assuming constant acceleration?
Solution: Average speed is given by:
\(\displaystyle \text{Average Speed} = \frac{\text{Total Distance}}{\text{Total Time}} = \frac{100 \text{ m}}{10 \text{ s}} = 10 \text{ m/s} \)
Since the acceleration is constant, the sprinter’s velocity at any time (t) is:
\(\displaystyle v(t) = u + at \)
where (u) is the initial velocity, (a) is the acceleration, and (t) is time. The initial velocity (u = 0) (starting from rest), and (t = 5) seconds. The final velocity (v) after 10 seconds (the total time) is:
\(\displaystyle v = \text{Average Speed} \times 2 = 20 \text{ m/s} \)
because under constant acceleration, the average speed is half of the final speed. Thus, the acceleration (a) is:
\(\displaystyle a = \frac{v}{t} = \frac{20 \text{ m/s}}{10 \text{ s}} = 2 \text{ m/s}^2 \)
The instantaneous speed at 5 seconds:
\(\displaystyle v(5) = 0 + 2 \times 5 = 10 \text{ m/s} \)
The sprinter’s average speed is 10 m/s, and the instantaneous speed at 5 seconds is also 10 m/s.
Problem 5: A particle moves along a straight line with a velocity given by (v(t) = 5t – 2). What is the displacement of the particle from (t = 1) s to (t = 4) s?
Solution: Displacement is found by integrating the velocity function over the given time interval:
\(\displaystyle \Delta x = \int_{1}^{4} (5t – 2) \, dt \)
Integrate:
\(\displaystyle \Delta x = \left[ \frac{5t^2}{2} – 2t \right]_{1}^{4} \)
\(\displaystyle = \left( \frac{5(4)^2}{2} – 2(4) \right) – \left( \frac{5(1)^2}{2} – 2(1) \right) \)
\(\displaystyle = \left( \frac{80}{2} – 8 \right) – \left( \frac{5}{2} – 2 \right) \)
\(\displaystyle = (40 – 8) – \left( \frac{5}{2} – 2 \right) \)
\(\displaystyle = 32 – \frac{1}{2} = 31.5 \text{ meters} \)
The displacement of the particle from (t = 1) s to (t = 4) s is 31.5 meters.
Problem 6: The position of a particle is given by (x(t) = 4t3 – 2t2 + 3t + 5). Find the instantaneous velocity at (t = 3) seconds.
Solution: Instantaneous velocity is the derivative of the position function:
\(\displaystyle v(t) = \frac{dx(t)}{dt} \)
\(\displaystyle v(t) = \frac{d}{dt} (4t^3 – 2t^2 + 3t + 5) \)
\(\displaystyle = 12t^2 – 4t + 3 \)
Now, substitute (t = 3):
\(\displaystyle v(3) = 12(3)^2 – 4(3) + 3 \)
\(\displaystyle = 12(9) – 12 + 3 \)
\(\displaystyle = 108 – 12 + 3 \)
\(\displaystyle = 99 \text{ m/s} \)
The instantaneous velocity at ( t = 3 ) seconds is 99 m/s.
FAQs
What is the difference between speed and velocity?
Speed is a scalar quantity that represents how fast an object is moving, regardless of direction, while velocity is a vector quantity that includes both speed and direction. Velocity indicates not only how fast an object is moving but also in which direction.
How do average velocity and average speed differ?
Average velocity considers both the displacement and the time taken, calculated as the displacement divided by the total time. Average speed, on the other hand, only considers the total distance traveled divided by the total time, irrespective of direction.
Can an object have a constant speed but changing velocity?
No, if an object has a constant speed, its velocity must also be constant unless it changes direction. Velocity includes both speed and direction, so any change in velocity, even if the speed remains constant, indicates a change in direction.
How do we calculate instantaneous velocity and instantaneous speed?
Instantaneous velocity is the velocity of an object at a specific instant in time, calculated as the limit of the average velocity as the time interval approaches zero. Instantaneous speed, similarly, is the speed of an object at a specific instant, calculated as the limit of the average speed as the time interval approaches zero.
Can the average speed of an object be greater than its average velocity?
Yes, it’s possible. If an object moves in different directions during its motion, resulting in a net displacement of zero, its average velocity would be zero. However, its average speed would still be nonzero, as it covers some distance over time.
How does acceleration relate to velocity and speed?
Acceleration is the rate of change of velocity. It can affect both the speed and direction of motion. Positive acceleration increases velocity (speeding up), negative acceleration (or deceleration) decreases velocity (slowing down), and changing direction also indicates acceleration.
Can an object have zero velocity but nonzero speed?
Yes, if an object changes direction but its displacement over time is zero, its velocity is zero. However, its speed would still be nonzero since speed only considers the magnitude of motion, irrespective of direction.
Can you provide a practical example illustrating the difference between speed and velocity?
Of course! Imagine a car driving around a circular track. Its speed remains constant throughout the lap since it covers the same distance in the same time interval. However, its velocity is constantly changing because its direction is changing as it moves around the curve, even though its speed remains the same.