Basic Properties of Electric Charge

Long before the term ‘electricity’ was coined, ancient civilizations noticed strange forces at play. The Greeks, for example, found that rubbing amber (or ‘elektron’) with fur attracted light objects like feathers. This was the earliest recorded observation of static electricity.

Fast forward to the 18th century, when the American polymath Benjamin Franklin conducted extensive research on electricity. He proposed the concept of positive and negative charges and suggested that electricity was not created by rubbing two different substances but rather transferred from one to the other. This was a revolutionary idea that changed the way we understood the electric charge.

In 1897, J.J. Thomson discovered the electron, a tiny particle with a negative charge, which provided evidence for the existence of electric charges as fundamental units of matter. This discovery was pivotal because it showed that electric charge is carried by specific particles, not just a property of certain materials.

George Stoney, in 1891, after discovering the quantized character of charge, proposed the unit ‘electron’ for this fundamental unit of electrical charge. This laid the groundwork for the concept of charge quantization, which means that charge comes in discrete packets rather than being continuous.

In 1909, Robert Millikan performed his famous oil-drop experiment, which measured the charge of a single electron with great accuracy. This experiment confirmed that electric charge is quantized and that the electron carries a fundamental unit of charge.

What is an Electric Charge?

Electric charge is a basic property of particles that causes them to experience a force when near other charged particles or in an electromagnetic field. There are two types of electric charges: positive and negative. Protons have a positive charge, electrons have a negative charge, and neutrons have no charge.

Imagine you’re at a dance party. Some people are naturally drawn to the dance floor, while others prefer to stay at the sidelines. Similarly, in the world of physics, electric charge is like an invisible force that can either pull particles together or push them apart.

Electric charge is a fundamental characteristic of particles that determines how they interact with each other and with electromagnetic fields. It’s one of the basic properties of the universe, just like mass or volume.

There are two types of electric charges:

• Positive charge: Think of it as the life of the party, represented by protons, which are found in the nucleus of an atom.
• Negative charge: This is the wallflower, represented by electrons, which orbit around the nucleus.

These charges interact with each other through forces of attraction and repulsion: Just like magnets, a positive charge will be attracted to a negative charge. Two positive charges, or two negative charges, will push away from each other.

This interaction is the foundation of electricity. When charges move, they create an electric current, which is what powers all the electronic devices you use every day.

Unit of Electric Charge: The unit of electric charge is the Coulomb (C). It’s named after Charles-Augustin de Coulomb, who quantified the force between two electric charges. When we talk about electric charge, it’s like discussing how much water is in a bucket. To measure water, we use liters or gallons, right? Similarly, to measure electric charge, we have a special unit called the Coulomb, symbolized by the letter ‘C’.

Now, imagine you’re filling a balloon with water. The amount of water that flows into the balloon each second can be measured, and that’s what a Coulomb does for an electric charge. Specifically, one Coulomb is the amount of electric charge that flows through a wire when an electric current of one ampere is applied for one second.

• Electric Current: This is like the flow of water in our balloon analogy. In electricity, it’s the flow of electric charge.
• Ampere: This is the unit that measures electric current, just like how meters measure distance.
• Second: That’s the time part. We’re looking at how much charge moves in one second.

So, if you have a current of one ampere, and it flows for one second, the amount of charge that has moved through the wire is one Coulomb. It’s a way to quantify the invisible stuff (charge) that makes all our electronic gadgets work.

Basic Properties of Electric Charge

Additive Property of Electric Charge

Electric charges can be added together. Imagine you’re at a party with a group of friends. Each friend has a certain number of balloons. Some have balloons tied to their wrists, and others don’t. Now, if you want to know how many balloons are at the party, you simply count all the balloons from each friend, right?

The additive property of electric charge works similarly. It tells us that the total charge of a system is the sum of all the individual charges it contains. Charges, like your friends’ balloons, can be counted together to give a total.

If you have three charges, let’s call them (q₁), (q₂), and (q₃), the total charge (Q ) of the system is simply the sum of these three:

\(\displaystyle Q = q_1 + q_2 + q_3 \)

This property is straightforward because electric charges are scalar quantities. This means they have magnitude (how much charge there is) but no direction, so you can add them up just like regular numbers.

For example:

• If one object has a charge of (+3) Coulombs and another has a charge of (-2) Coulombs, the total charge when you bring them together is (+1) Coulomb.
• If you have a collection of particles, and some have positive charges while others have negative charges, you add up all the positives and negatives to find the total charge of the group.

In essence, the additive property of electric charge allows us to calculate the net charge in any situation by simply adding up all the individual charges, taking into account their signs (positive or negative). It’s like tallying up points in a game, where some points add to your score and others subtract from it.

Conservative Nature of Charge

To understand the conservative nature of the electric charge, let’s think of it in terms of something very familiar: money. Imagine you have a piggy bank. You can put money in and take money out, but the amount of money inside the piggy bank doesn’t change unless you do one of these actions. Similarly, in physics, the conservative nature of charge means that the total amount of charge in an isolated system doesn’t change on its own.

The principle of conservation of charge states that the total electric charge in an isolated system remains constant over time. No matter what reactions or interactions happen within that system, the amount of positive charge minus the amount of negative charge always adds up to the same number.

This property is fundamental to the laws of physics. Just like energy or momentum, the charge is a conserved quantity. It’s a rule of the universe that has been observed in countless experiments and has never been proven wrong.

• If you have a system with a certain amount of charge, you can’t create more charge or destroy any of it. You can only move it around within the system.
• In any chemical reaction or physical process, the net charge before the process is equal to the net charge after the process.

Example: When you rub a balloon on your hair, electrons move from your hair to the balloon, giving the balloon a negative charge and your hair a positive charge. The total charge hasn’t changed; it has only been redistributed. So, the conservative nature of charge is like a law of “charge accounting” that ensures the total charge in any closed system is always balanced.

Quantization of Charge

Think of electric charge as if it were currency. In many countries, the smallest unit of currency is the cent. You can have 1 cent, 50 cents, or 100 cents, but you can’t have a fraction of a cent in your pocket. Similarly, the electric charge comes in discrete packets called elementary charges. You can have one elementary charge, two, three, and so on, but not half an elementary charge.

Quantization of charge means that the charge (q) is always an integer multiple of the elementary charge (e), which is approximately \(\displaystyle 1.602 \times 10^{-19} \) Coulombs. The charge on any object is quantized and can be written as:

\(\displaystyle q = n \times e \)

where (n) is an integer (…, -3, -2, -1, 0, 1, 2, 3, …), and (e) is the elementary charge.

Just like you can’t walk into a store and pay with half a cent, particles can’t have a fractional elementary charge because that’s not how nature works. This rule is universal and has been confirmed by countless experiments.

Examples:

• When you comb your hair and it sticks to the comb, that’s because electrons (each with one elementary charge) have moved from your hair to the comb, leaving each with a quantized net charge.
• The static shock you get when touching a doorknob is due to the transfer of a quantized number of electrons from you to the doorknob (or vice versa).

The quantization of charge is a fundamental rule of the universe, ensuring that all observable charges are tidy multiples of a single, indivisible unit of charge.

Other Properties of Electric Charge

Charge is Transferable

Charge can be transferred from one object to another, usually by direct contact or through a conducting medium. Imagine you have a bunch of stickers. You can stick them on your notebook, or your phone, or even give some to your friends. The stickers haven’t changed; they’ve just moved to a new place. This is similar to how electric charge can be transferred from one object to another.

The idea that charge is transferable means that electric charge can move from one object to another. This can happen in various ways, such as through direct contact or by the movement of electrons, which are the carriers of charge.

How Does Charge Get Transferred?

• By Touching (Conduction): When two objects come into contact, electrons can move from one to the other. If you rub a balloon on your hair, electrons transfer from your hair to the balloon, giving it a negative charge.
• By Proximity (Induction): Sometimes, just bringing a charged object close to a neutral one can cause electrons in the neutral object to rearrange themselves, creating a positive side and a negative side².

Understanding that charge is transferable helps explain everyday phenomena:

• Why do you get a shock after walking across a carpet and touching a doorknob? Because you’ve picked up extra electrons from the carpet, and they jump to the doorknob when you touch it.
• Why does your hair stand up when you take off a hat? Because charges have been transferred between your hair and the hat, causing the strands of hair to repel each other.

Charge is Always Associated with Mass

Charges are carried by particles that have mass, like protons and electrons. Think of a car. A car can move, carry people, and interact with other cars. Now, imagine if someone told you there’s an invisible car that can do all these things but doesn’t have any weight. You’d find it hard to believe, right? That’s because we expect things that have an effect on the physical world to have some substance.

In the world of physics, electric charge is like a car. It can move around, it can cause forces, and it can do work. But just like a car, the charge isn’t something that exists on its own; it’s always a property of something else that has mass. Here’s why:

• Particles Carry Charge: In the universe, charges are carried by particles, and all particles have mass. For example, electrons carry a negative charge and have a small mass, while protons carry a positive charge and have a larger mass.
• No Massless Charge: We’ve never found a charge without mass. Even in the tiniest particles we know, like quarks, which make up protons and neutrons, the charge comes with mass.

Charge is always associated with mass helps us make sense of how the universe works. It explains why charged particles behave the way they do under the influence of forces like gravity and electromagnetism.

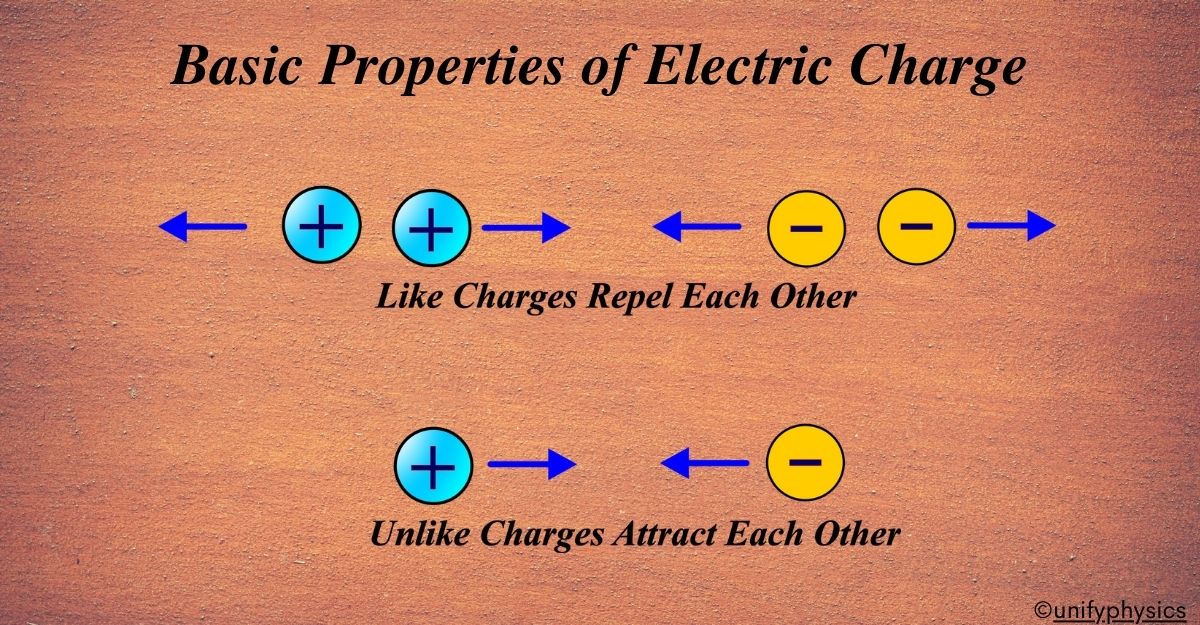
Like Charges Repel Each Other and Unlike Charges Attract Each Other

This is the basic principle of electrostatics. It explains why charged objects behave the way they do when brought close to each other. Imagine you’re at a social gathering. Some people get along well and naturally group together, while others prefer to keep their distance. This social dynamic is similar to how electric charges interact with each other.

Like Charges Repel: Just like two people who don’t get along might avoid each other, two electric charges of the same type (both positive or both negative) will repel, or push away, from each other. It’s as if they have a personal bubble that they don’t want others to invade.

Unlike Charges Attract: On the other hand, just like two people who are drawn to each other might come together, a positive charge and a negative charge will attract, or pull toward, each other. This attraction is like a handshake or a hug; it’s a natural force that brings them together.

This behavior is due to the electric force, a fundamental force of nature. According to Coulomb’s law, the force between two charges is directly proportional to the product of their magnitudes and inversely proportional to the square of the distance between them. The direction of the force depends on whether the charges are like or unlike.

Accelerated Charges Radiate Energy

When charged particles accelerate, they emit electromagnetic radiation. This is the basis for technologies like radio and X-rays. Imagine you’re on a swing, and as you go back and forth, you create ripples in the air. The faster you swing, the bigger the ripples. Now, think of these ripples as energy radiating away from you. This is similar to what happens with electric charges.

When an electric charge speeds up, slows down, or changes direction (which means it’s accelerating), it doesn’t just move silently through space. Instead, it sends out ripples in the electromagnetic field around it. These ripples are known as electromagnetic radiation.

• Disturbance in the Field: Just like your swinging creates ripples in the air, an accelerating charge disturbs the electromagnetic field around it.
• Energy in Waves: These disturbances travel outward in waves, carrying energy away from the charge. The faster the charge accelerates, the more energy is radiated.

The term “radiate” is used because the energy spreads out in all directions, just like light radiating from a bulb or heat from a fire.

Also Read: Electric Charge

Solved Examples

Question: Two small spheres have charges of (+3×10^-6) C and (-8×10^-6) C. They are touched together and then separated. What is the final charge on each sphere?

Solution: The total initial charge is the sum of the individual charges:

\(\displaystyle Q_{total} = (+3 \times 10^{-6}) + (-8 \times 10^{-6}) = -5 \times 10^{-6} \text{ C}\)

When the spheres are touched together, the charges redistribute evenly:

\(\displaystyle Q_{final} = \frac{Q_{total}}{2} = \frac{-5 \times 10^{-6}}{2} = -2.5 \times 10^{-6} \text{ C}\)

Answer: Each sphere will have a charge of (\(\displaystyle -2.5 \times 10^{-6} \)) C.

Question: In a closed system, a charge of (\(\displaystyle +6 \times 10^{-6} \)) C is transferred from object A to object B. If the initial charge on object B was (\(\displaystyle -2 \times 10^{-6} \)) C, what is the final charge on object B?

Solution: Since charge is conserved, the final charge on object B will be the initial charge plus the transferred charge:

\(\displaystyle Q_{B_{final}} = Q_{B_{initial}} + Q_{transferred}\)

\(\displaystyle Q_{B_{final}} = (-2 \times 10^{-6}) + (+6 \times 10^{-6}) = +4 \times 10^{-6} \text{ C}\)

Answer: The final charge on object B is (\(\displaystyle +4 \times 10^{-6} \)) C.

Question: If an object loses (\(\displaystyle 5 \times 10^{13} \)) electrons, what is the net charge gained by the object?

Solution: The charge of one electron is approximately (\(\displaystyle -1.602 \times 10^{-19} \)) C. The net charge gained is:

\(\displaystyle Q = n \times e\)

\(\displaystyle Q = 5 \times 10^{13} \times (-1.602 \times 10^{-19})\)

\(\displaystyle Q = -8.01 \times 10^{-6} \text{ C}\)

Answer: The net charge gained by the object is (\(\displaystyle -8.01 \times 10^{-6} \)) C.

Question: Two charges, (\(\displaystyle q_1 = +1 \times 10^{-6} \)) C and (\(\displaystyle q_2 = -3 \times 10^{-6} \)) C, are placed 0.5 meters apart. Calculate the force between them.

Solution: Using Coulomb’s law:

\(\displaystyle F = k \frac{|q_1 \times q_2|}{r^2}\)

Where (k) is Coulomb’s constant (\(\displaystyle 8.9875 \times 10^9 \)) Nm²/C²), we get:

\(\displaystyle F = 8.9875 \times 10^9 \times \frac{|1 \times 10^{-6} \times -3 \times 10^{-6}|}{(0.5)^2}\)

\(\displaystyle F = 8.9875 \times 10^9 \times \frac{3 \times 10^{-12}}{0.25}\)

\(\displaystyle F = 8.9875 \times 10^9 \times 12 \times 10^{-12}\)

\(\displaystyle F = 107.85 \text{ N}\)

Answer: The force between the charges is 107.85 N.

Question: A charge of (\(\displaystyle +2 \times 10^{-6} \)) C is placed in a uniform electric field that exerts a force of (0.04) N on it. Calculate the magnitude of the electric field.

Solution: The electric field (E) is defined as the force (F) per unit charge (q):

\(\displaystyle E = \frac{F}{q}\)

\(\displaystyle E = \frac{0.04}{2 \times 10^{-6}}\)

\(\displaystyle E = 2 \times 10^4 \text{ N/C}\)

Answer: The magnitude of the electric field is (\(\displaystyle 2 \times 10^4 \)) N/C.

Question: A parallel-plate capacitor with a capacitance of (5) µF is charged to a potential difference of (100 ) V. Calculate the energy stored in the capacitor.

Solution: The energy ( U ) stored in a capacitor is given by:

\(\displaystyle U = \frac{1}{2} C V^2\)

Where (C) is the capacitance and (V) is the potential difference:

\(\displaystyle U = \frac{1}{2} \times 5 \times 10^{-6} \times (100)^2\)

\(\displaystyle U = \frac{1}{2} \times 5 \times 10^{-6} \times 10^4\)

\(\displaystyle U = 2.5 \times 10^{-2} \text{ J}\)

Answer: The energy stored in the capacitor is (\(\displaystyle 2.5 \times 10^{-2} \)) J.

FAQs