In the 18th century, a Swiss mathematician named Daniel Bernoulli was about to make a discovery that would change our understanding of how fluids behave. He was part of the famous Bernoulli family, a dynasty of mathematicians that had already made significant contributions to the field.
In 1738, Daniel Bernoulli published a book called Hydrodynamica, which laid the foundation for what we now know as Bernoulli’s Principle. But the story doesn’t end there. While Daniel Bernoulli was the first to describe how pressure decreases when the flow speed increases, it was another brilliant mind, Leonhard Euler, who later derived the equation in its commonly used form in 1752.
The plot thickens with a bit of family drama. Daniel’s father, Johann Bernoulli, was also a renowned mathematician. When Daniel published his groundbreaking work, it sparked a rivalry between father and son. Johann published his own book, Hydraulics, almost simultaneously with Daniel’s work, leading to a competitive atmosphere in the Bernoulli household.
Daniel Bernoulli’s work stood the test of time despite the family feud. His principle became a cornerstone in fluid dynamics, explaining phenomena in various fields, from aerodynamics to medicine. It’s a testament to the power of curiosity and the pursuit of knowledge, showing how one idea can flow through time and impact the world in countless ways.
What is Bernoulli’s Principle?
Bernoulli’s Principle states that in a flowing fluid (liquid or gas), the pressure within the fluid decreases as the speed of the fluid increases. This principle is a manifestation of the conservation of energy principle for fluids in motion.
Think of a river flowing down a mountain. In some places, the river runs wide and the water moves slowly. In other places, the river narrows and the water rushes through quickly. Bernoulli’s Principle is like the rulebook that this river follows.
Here’s the key idea: As the river narrows, the water speeds up, and the pressure drops. Why? Because the water has less room to move around, so it has to go faster to get through the tight space. And when it goes faster, it doesn’t push as hard on the riverbanks – that’s the pressure dropping.
Now, replace the river with any fluid, like air or water in a pipe, and the same rules apply. When the fluid speeds up, the pressure within it goes down. This is why an airplane wing is shaped the way it is – the air moves faster over the top, creating lower pressure, and that difference in pressure lifts the plane into the sky.
So, in a nutshell, Bernoulli’s Principle is about the relationship between the speed of a fluid and the pressure it exerts. Faster fluid equals lower pressure, and slower fluid equals higher pressure. It’s a fundamental concept that explains a lot of the fluid behavior we see in both nature and technology.
Bernoulli’s Principle Formula
To understand Bernoulli’s Principle Formula, think of it as a balance equation for a fluid’s energy. It tells us that as a fluid moves, its energy is conserved and distributed among different forms. Here’s a simple way to look at it:
The faster the fluid moves, the less pressure it exerts. This is because some of the fluid’s energy is used up in motion, leaving less energy to exert as pressure. It’s like having a fixed amount of energy currency; if you spend more on movement, you have less to spend on pressure.
This principle helps us predict how fluids will behave in different situations, like when they flow through pipes of varying sizes or over airplane wings. It’s a fundamental concept that shows the fluid’s speed and pressure are interconnected, and understanding this relationship is key to mastering fluid dynamics.
Imagine you’re at a water park, and there’s a giant slide with water flowing down it. Now, let’s break down the formula that explains what’s happening with the water as it flows and twists down the slide.
Bernoulli’s Principle Formula is like a recipe that tells us how the speed of the water, its height from the ground, and the pressure all mix together. Here’s the formula:
\(\displaystyle\begin{equation}\label{eqn:1}\boxed{\boldsymbol{p + \frac{1}{2} \rho v^2 + \rho gh = \text{constant} }} \end{equation}\)
- (p): This is the pressure of the water. It’s like how hard the water is pushing against the walls of the slide.
- (ρ): This is the density of the water. It tells us how much stuff is packed into a certain amount of water.
- (v): This is the speed of the water. When you see the water rushing fast, that’s the (v) in action.
- (g): This is gravity, the force that pulls everything down towards the earth.
- (h): This is the height of the water from the ground. The higher up the slide you are, the bigger (h) is.
Now, the formula says that if you add up the pressure, the water’s kinetic energy that’s the \(\displaystyle \frac{1}{2} \rho v^2 \) part, and the potential energy from the height the \(\displaystyle (\rho gh) part\), it will always equal the same number, no matter where you are on the slide. This “constant” is like the total energy budget the water has to work with.
So, if the water goes faster (increases (v), it can’t push as hard (decreases (p), and if it goes higher (increases (h), it also can’t push as hard. The water has to balance its speed, height, and pushiness to keep the total energy the same.
In simpler terms, the formula tells us that the water can’t be super fast, super high, and super pushy all at the same time. It has to choose two and trade off the third. That’s the heart of Bernoulli’s Principle, and it’s what keeps the water flowing smoothly down the slide.
Bernoulli’s Equation Derivation
Bernoulli’s equation can be derived from the conservation of energy. It considers the work done by the fluid and the changes in kinetic and potential energy as the fluid moves through different heights and areas in a pipe.
The work done on the fluid as it moves from point A to B is the force applied over a distance. This can be expressed as the difference in pressure work at points A and B:
\(\displaystyle dW = p_1 A_1 dx_1 – p_2 A_2 dx_2 \)
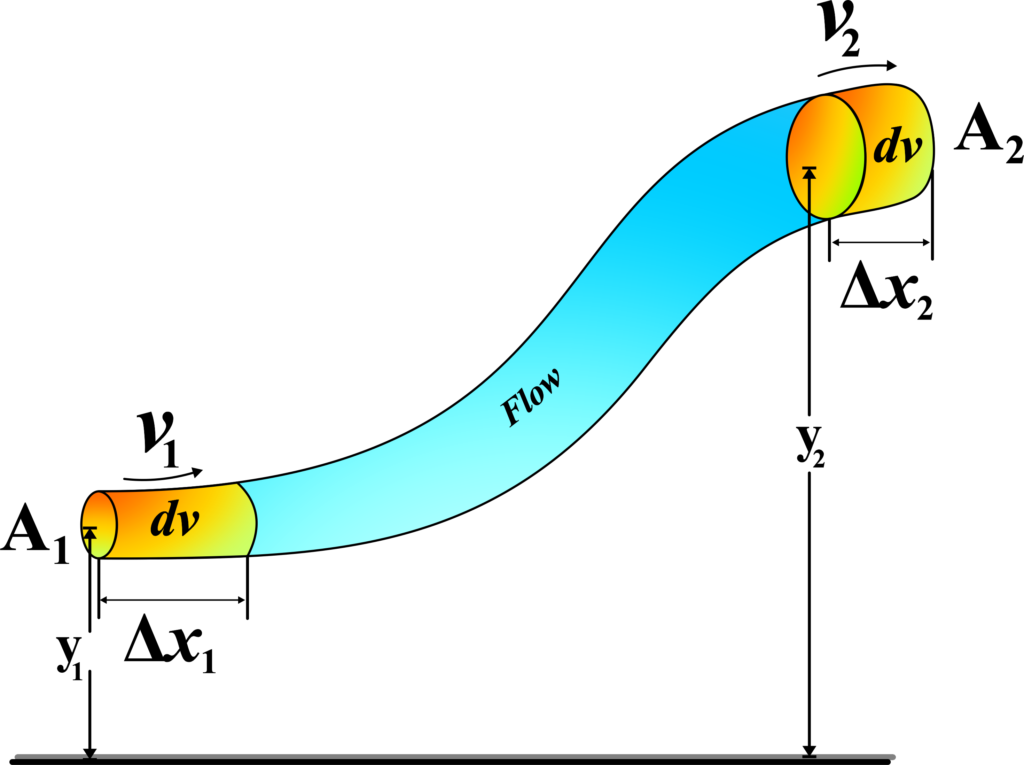
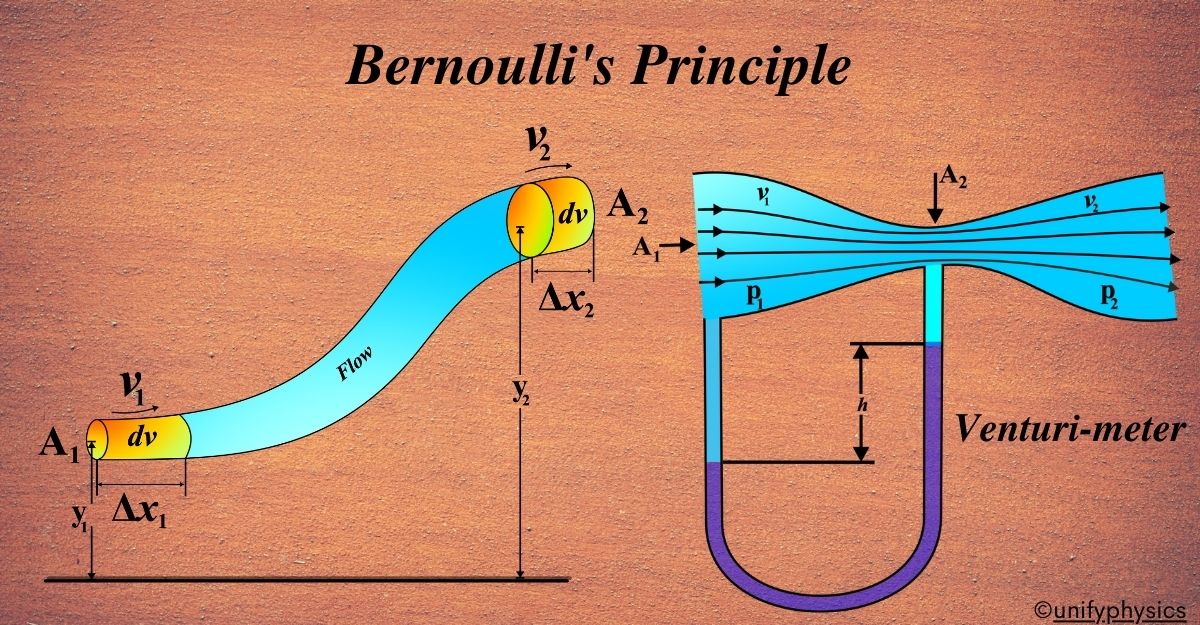
The work done on the fluid results in a change in kinetic energy and gravitational potential energy. The change in kinetic energy (KE) for a small volume (dv) of fluid with density (ρ) is:
\(\displaystyle dKE = \frac{1}{2} \rho dv (v_2^2 – v_1^2) \)
The change in potential energy (PE) as the fluid moves from height (Y1) to (Y2) is:
\(\displaystyle dPE = \rho g dv (Y_2 – Y_1) \)
The total mechanical energy (sum of kinetic and potential energy) at point A must equal the total mechanical energy at point B, plus the work done on the fluid:
\(\displaystyle KE_1 + PE_1 + dW = KE_2 + PE_2 \)
We substitute the expressions for work done, change in kinetic energy, and change in potential energy into the conservation of energy equation:
\(\displaystyle \frac{1}{2} \rho v_1^2 + \rho g Y_1 + p_1 = \frac{1}{2} \rho v_2^2 + \rho g Y_2 + p_2 \)
Since the density (ρ) is constant for an incompressible fluid and the volume (dv) cancels out, we can simplify the equation to:
\(\displaystyle p_1 + \frac{1}{2} \rho v_1^2 + \rho g Y_1 = p_2 + \frac{1}{2} \rho v_2^2 + \rho g Y_2 \)
We can generalize this for any two points along the streamline in a steady flow, giving us Bernoulli’s Equation:
\(\displaystyle\begin{equation}\label{eqn:2}\boxed{\boldsymbol{p + \frac{1}{2} \rho v^2 + \rho g Y = \text{constant} }} \end{equation}\)
This equation shows that the sum of the pressure energy, kinetic energy per unit volume, and gravitational potential energy per unit volume remains constant along a streamline. It’s a powerful statement about the conservation of energy in fluid flow.
Principle of Continuity
The Principle of Continuity states that for an incompressible fluid, the product of the cross-sectional area of the pipe and the velocity of the fluid is constant. This means that as the area decreases, the velocity must increase, and vice versa.
Imagine you’re at a water park, and there’s a long, winding water slide with a constant flow of water. The Principle of Continuity is like the rule that the water follows as it slides down from the top to the bottom.
Here’s a simple idea: The amount of water going into the slide at the top has to be the same as the amount of water coming out at the bottom. This is because water, like most fluids we deal with in everyday life, can’t just disappear or magically increase in quantity.
Now, let’s say the slide gets narrower in some parts. Since the same amount of water has to pass through every second, the water has to move faster in the narrow parts to keep up. It’s like when you’re in a crowd, and everyone has to move quickly to get through a narrow door.
In physics terms, the Principle of Continuity says that the flow rate of the fluid must stay constant. So, if the cross-sectional area of the slide (or pipe) gets smaller, the velocity of the water must increase, and vice versa.
Mathematically, we express this principle with a simple formula:
\(\displaystyle\begin{equation}\label{eqn:3}\boxed{\boldsymbol{A_1 \times v_1 = A_2 \times v_2 }} \end{equation}\)
- (A1) and (A2) are the cross-sectional areas of the slide at two different points,
- (v1) and (v2) are the velocities of the water at those points.
This formula tells us that the product of the area and velocity at one point is equal to the product of the area and velocity at any other point along the slide.
So, the Principle of Continuity is all about maintaining balance. It ensures that what goes in must come out, and it helps us understand how fluids behave in different situations, like in pipes, rivers, and yes, even water slides!
Applications of Bernoulli’s Principle and Equation
The Venturi Tube and Bernoulli’s Principle
A Venturi Tube is a device that narrows down in the middle, creating a region of lower pressure that can be used to measure the flow rate of the fluid passing through it. This is what a Venturi Tube looks like. Now, let’s see how it works with Bernoulli’s Principle:
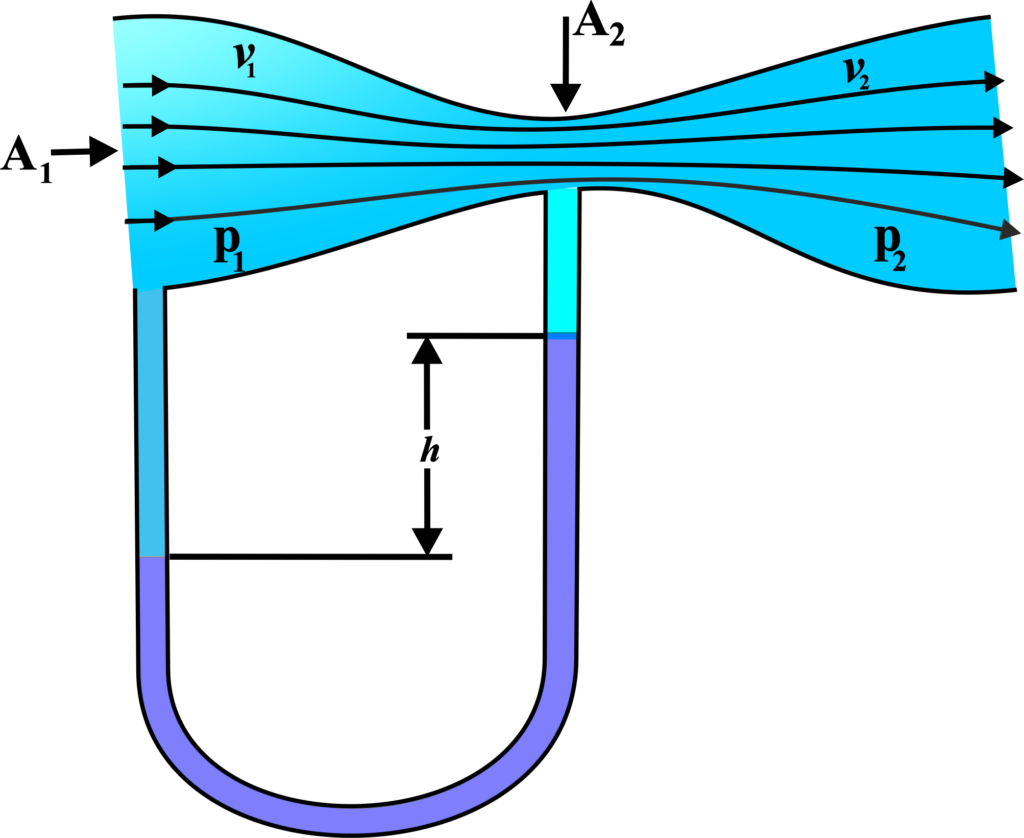
When a fluid enters the narrow part of the tube, it speeds up. This happens because the fluid has less space to flow through, so it has to move faster to get through the tight spot. According to Bernoulli’s Principle, where the fluid speed increases, the pressure decreases. So, in the narrow part of the Venturi Tube, the pressure is lower than in the wider parts.
This change in pressure is really useful. By measuring the pressure difference between the narrow and wide parts of the tube, we can figure out how fast the fluid is flowing. This is how a Venturi Tube can be used to measure fluid speed. Venturi Tubes are used in various devices. For example, they help measure the flow rate of liquids and gases in pipes. They’re also used in carburetors in cars to mix air and fuel, and in airplane instruments to measure airspeed.
So, the Venturi Tube is a practical example of Bernoulli’s Principle in action. It shows us how changes in fluid speed and pressure can be used to create useful tools for everyday applications.
Derivation:
We know that Bernoulli’s Equation relates the pressure, velocity, and height of a fluid at two points along its path. For a horizontal Venturi Tube, the height remains constant, so we can ignore the height term:
\(\displaystyle p + \frac{1}{2} \rho v^2 = \text{constant} \)
The Continuity Equation tells us that the flow rate must be constant throughout the tube, so (A1 v1 = A2 v2), where (A) is the cross-sectional area and (v) is the velocity of the fluid.
Let’s call the pressure (p1) and the velocity (v1). The cross-sectional area here is (A1). The pressure drops to (p2) and the velocity increases to (v2). The cross-sectional area is (A2).
Using Bernoulli’s Equation, we can set up the following relationship at Points 1 and 2:
\(\displaystyle p_1 + \frac{1}{2} \rho v_1^2 = p_2 + \frac{1}{2} \rho v_2^2 \)
We want to find the velocity at the narrow section, so we use the Continuity Equation to express (v2) in terms of (v1):
\(\displaystyle v_2 = \frac{A_1}{A_2} v_1 \)
Now we substitute (v2) into Bernoulli’s Equation and solve for (v1):
\(\displaystyle p_1 + \frac{1}{2} \rho v_1^2 = p_2 + \frac{1}{2} \rho \left(\frac{A_1}{A_2} v_1\right)^2 \)
After rearranging the terms, we can solve for (v1) in terms of the pressures and areas:
\(\displaystyle v_1 = \sqrt{\frac{2(p_1 – p_2)}{\rho \left(1 – \left(\frac{A_1}{A_2}\right)^2\right)}} \)
The flow rate (Q) is the product of the cross-sectional area and the velocity at any point, so we can express it as:
\(\displaystyle\begin{equation}\label{eqn:4}\boxed{\boldsymbol{ Q = A_1 v_1 = A_1 \sqrt{\frac{2(p_1 – p_2)}{\rho \left(1 – \left(\frac{A_1}{A_2}\right)^2\right)}}}} \end{equation}\)
This final expression allows us to calculate the flow rate of the fluid in the Venturi Tube by measuring the pressure difference between the wide and narrow sections and knowing the areas of these sections.
Lift on Airplane Wings and Bernoulli’s Principle
Airplane wings are designed with a special shape called an airfoil. The top surface of the wing is curved, while the bottom is relatively flat. As the plane moves forward, air flows over and under the wing. Due to the wing’s shape, the air has to travel a longer path over the top surface, causing it to speed up to meet up with the air flowing under the wing.
According to Bernoulli’s Principle, faster-moving air leads to lower pressure. So, the pressure on top of the wing is less than the pressure below the wing. This pressure difference creates an upward force on the wing, known as lift. It’s this lift that counteracts the weight of the airplane and keeps it in the sky.
Bernoulli’s Equation can be used to calculate the pressure difference between the top and bottom of the wing, which is essential for determining the amount of lift generated.
Blood Pressure and Bernoulli’s Principle
Bernoulli’s Principle and Equation provide a framework for understanding the relationship between the velocity of blood flow and the pressure exerted by the blood on arterial walls, which is fundamental in the measurement and understanding of blood pressure.
Just like air flowing over an airplane wing or water through a pipe, blood flowing through our arteries has properties of speed and pressure that can be described by Bernoulli’s Principle. When blood moves through our arteries, it does so at varying speeds and pressures. In narrower parts of the artery, like when there’s a constriction, blood speeds up, and according to Bernoulli’s Principle, the pressure in that region decreases.
Medical devices that measure blood pressure, like a sphygmomanometer, indirectly use Bernoulli’s Principle. When the cuff inflates, it constricts the artery, and as it deflates, blood starts flowing again, changing speed and pressure. By listening to the changes in blood flow with a stethoscope, a doctor can determine the systolic and diastolic blood pressure.
The equation helps us understand that as the velocity of blood flow increases, the lateral pressure against the artery walls decreases. This is important when considering areas of the cardiovascular system where blood velocity is high, such as when exiting the heart.
In clinical settings, Bernoulli’s Principle is used to estimate blood flow velocities and pressures within the heart and vessels using ultrasound technology, which can help diagnose conditions like valve stenosis or other cardiovascular diseases.
Relation between Conservation of Energy and Bernoulli’s Equation
Bernoulli’s equation is a form of the conservation of energy principle for fluid flow, relating the mechanical energy per unit volume in terms of pressure, kinetic energy, and potential energy.
This fundamental principle in physics tells us that energy cannot be created or destroyed, only transformed from one form to another. In a closed system, the total energy remains constant. When we apply the Conservation of Energy to the flow of fluids, we consider the fluid’s kinetic energy (due to its motion), potential energy (due to its position or height), and the energy associated with pressure.
This equation is a mathematical representation of the Conservation of Energy for flowing fluids. It tells us that the sum of the fluid’s pressure energy, kinetic energy, and potential energy remains constant along a streamline.
\(\displaystyle\begin{equation}\label{eqn:5}\boxed{\boldsymbol{ p + \frac{1}{2} \rho v^2 + \rho gh = \text{constant}}} \end{equation}\)
- (p) is the pressure energy per unit volume,
- \(\displaystyle\frac{1}{2} \rho v^2\) is the kinetic energy per unit volume (with (\rho) being the fluid density and (v) the velocity),
- (ρ gh) is the potential energy per unit volume (with (g) being the acceleration due to gravity and (h) the height above a reference point).
The Insight
- Pressure Energy: If the fluid is under high pressure, it has more potential to do work.
- Kinetic Energy: If the fluid is moving fast, it has more kinetic energy.
- Potential Energy: If the fluid is at a higher elevation, it has more potential energy due to gravity.
As the fluid flows, it may exchange energy between these forms, but the total energy remains constant if we ignore friction and other losses. This is how Bernoulli’s Equation embodies the Conservation of Energy in fluid dynamics.
Conservation of Energy at Constant Depth
This principle tells us that in a closed system, energy can neither be created nor destroyed; it can only change forms. For fluids, this means the total energy (kinetic, potential, and pressure energy) remains constant along a streamline.
At a constant depth, the height of the fluid remains the same, so the potential energy due to gravity doesn’t change. Bernoulli’s Equation simplifies because the term involving height (ρ gh) remains constant and can be ignored for our purposes.
Without the height term, Bernoulli’s Equation at a constant depth looks like this:
\(\displaystyle\begin{equation}\label{eqn:6}\boxed{\boldsymbol{p + \frac{1}{2} \rho v^2 = \text{constant} }} \end{equation}\)
- (p) is the pressure energy per unit volume,
- \(\displaystyle\frac{1}{2} \rho v^2 \) is the kinetic energy per unit volume.
- At Constant Depth: Since the height doesn’t change, any change in the fluid’s speed will directly affect its pressure. If the fluid speeds up, its kinetic energy increases, and to conserve energy, its pressure must decrease.
- Energy Balance: The fluid’s total mechanical energy is still conserved, but now it’s shared between only the kinetic and pressure energies.
Think of a flat river where the depth doesn’t change much. If the river narrows and the water speeds up, the pressure against the riverbed and banks decreases. This is the river following the Conservation of Energy, as described by Bernoulli’s Equation at a constant depth.
Bernoulli’s Equation for Static Fluids
When we talk about static fluids, we mean fluids that are not moving. In this case, Bernoulli’s Equation simplifies because there is no fluid flow, and therefore, no kinetic energy related to movement.
Here’s the simplified equation for static fluids:
\(\displaystyle\begin{equation}\label{eqn:7}\boxed{\boldsymbol{ P = \rho g h}} \end{equation}\)
- (P) is the pressure at a certain depth in the fluid,
- (ρ) is the density of the fluid,
- (g) is the acceleration due to gravity,
- (h) is the height (or depth) of the fluid above the point where the pressure is being measured.
The equation tells us that the pressure at any point in a static fluid depends only on the depth of the fluid, its density, and gravity.
- Pressure Increases with Depth: In a body of static fluid, the pressure increases as you go deeper. This is because the weight of the fluid above adds to the pressure experienced at lower levels.
- No Movement, No Kinetic Energy: Since the fluid isn’t moving, we don’t have to consider its velocity, which means the kinetic energy term \(\displaystyle\frac{1}{2} \rho v^2\) is zero.
Think of a swimming pool: the pressure at the bottom of the pool is greater than at the top because there’s more water pushing down due to gravity. This is why your ears might feel more pressure when you dive deep into the water.
Also Read: Streamline And Turbulent Flow
Limitations of Bernoulli’s Principle
Bernoulli’s Principle assumes that the fluid is incompressible and there are no energy losses due to friction (viscous forces). It does not apply to flows with significant viscosity or compressibility.
- Incompressible Fluids: Bernoulli’s Principle is ideal for fluids that can’t be compressed. This means it works best for liquids like water but not as well for gases that can be squeezed into a smaller space.
- Streamline Flow: The principle applies to streamline or laminar flow, where the fluid moves in smooth paths or layers. It doesn’t hold up in turbulent flow, which is chaotic and involves eddies and swirls.
- No Viscosity: Bernoulli’s Principle assumes that the fluid has no viscosity, which is a measure of its thickness or stickiness. In real life, most fluids have some viscosity, and this can affect the flow and pressure.
- No Energy Loss: The principle assumes that there’s no loss of energy as the fluid moves. However, in reality, some energy is always lost due to friction and other factors.
- No External Forces: It assumes that no external forces, like pumps or fans, are adding energy to the fluid. It only considers the fluid’s own motion and gravity.
- Angular Momentum Ignored: Bernoulli’s Principle doesn’t take into account the angular momentum of the fluid, which can be significant in cases like cyclones or when the fluid is spinning.
- Steady Flow: The principle assumes that the flow is steady, meaning that the velocity of the fluid at any point doesn’t change over time. But in many real-world situations, flow can be unsteady.
Solved Examples
Example 1: Water flows through a garden hose with a diameter of ( 2 cm) at a speed of ( 1 ,m/s). If the hose is replaced with a nozzle of diameter (0.5 ,cm), what is the speed of water exiting the nozzle?
Solution: Using the equation of continuity \(\displaystyle A_1 v_1 = A_2 v_2 \), where (A1) and (A2) are the cross-sectional areas of the hose and nozzle respectively, and (v1) and (v2) are the velocities of water in the hose and nozzle respectively, we can solve for (v2):
\(\displaystyle\pi (0.01)^2 \cdot 1 = \pi (0.0025)^2 \cdot v_2\)
\(\displaystyle v_2 = \frac{(0.01)^2}{(0.0025)^2}\)
\(\displaystyle v_{2} = 16 \, \text{m/s}\)
Example 2: A Venturi tube is used to measure the speed of a fluid. If the difference in height of the mercury column in the U-tube manometer attached to the Venturi tube is (0.15 ,m), and the diameters at the two points are (0.1, m) and (0.05 , m) respectively, find the speed of the fluid at the wider section. Assume the density of mercury is (13,600 , kg/m3 ) and the density of the fluid is (1000 , kg/m3).
Solution: According to the Venturi effect:
\(\displaystyle P_{1} – P_{2} = \rho_{\text{fluid}} g h\)
\(\displaystyle P_{1} – P_{2} = \rho_{\text{mercury}} g \Delta h\)
Where (∆ h) is the height difference in the mercury column. Using Bernoulli’s equation and the continuity equation:
\(\displaystyle P_{1} + \frac{1}{2}\rho v_1^2 = P_2 + \frac{1}{2}\rho v_2^2\)
\(\displaystyle v_2 = \frac{A_1}{A_2} v_{1}\)
Substituting (P1 – P2) and (v2) into Bernoulli’s equation and solving for (v1):
\(\displaystyle\rho_{\text{fluid}} g h = \frac{1}{2}\rho_{\text{fluid}} \left(\frac{A_1}{A_2}\right)^2 v_1^2 – \frac{1}{2}\rho_{\text{fluid}} v_1^2\)
\(\displaystyle 1000 \cdot 9.81 \cdot 0.15 = \frac{1}{2} \cdot 1000 \left(\frac{0.1}{0.05}\right)^2 v_1^2 – \frac{1}{2} \cdot 1000 v_1^2\)
\(\displaystyle 1471.5 = 2000 v_1^2 – 500 v_1^2\)
\(\displaystyle v_1 = \sqrt{\frac{1471.5}{1500}}\)
\(\displaystyle v_1 = 0.99 \, \text{m/s}\)
Example 3: A water tank has an open top and is filled to a height of ( 5 ,m). Calculate the pressure at the bottom of the tank.
Solution: Using Bernoulli’s equation for static fluids:
\(\displaystyle P + \rho gh = P_{\text{atm}}\)
Where (Patm) is the atmospheric pressure at the open top of the tank and is (101,325 , Pa). Solving for (P) at the bottom:
\(\displaystyle P = P_{\text{atm}} + \rho gh\)
\(\displaystyle P = 101,325 + 1000 \cdot 9.81 \cdot 5\)
\(\displaystyle P = 101,325 + 49,05\)
\(\displaystyle P = 150,375 \, \text{Pa}\)
Example 4: A U-tube manometer contains mercury and is connected to a gas tank. If the difference in mercury levels in the two arms of the U-tube is (0.76, m), calculate the pressure of the gas in the tank. Assume atmospheric pressure is (101,325 ,Pa) and the density of mercury is (13,600 , kg/m3).
Solution: The pressure difference between the two arms is due to the height difference in mercury:
\(\displaystyle P_{\text{gas}} – P_{\text{atm}} = \rho_{\text{Hg}} g h\)
Solving for (Pgas):
\(\displaystyle P_{\text{gas}} = P_{\text{atm}} + \rho_{\text{Hg}} g h\)
\(\displaystyle P_{\text{gas}} = 101,325 + 13,600 \cdot 9.81 \cdot 0.76\)
\(\displaystyle P_{\text{gas}} = 101,325 + 101,366.16\)
\(\displaystyle P_{\text{gas}} = 202,691.16 \, \text{Pa}\)
FAQs
What is Bernoulli’s Principle, and how does it relate to fluid dynamics?
Bernoulli’s Principle states that in a flowing fluid, an increase in the speed of the fluid occurs simultaneously with a decrease in pressure or a decrease in the fluid’s potential energy. Conversely, a decrease in speed is accompanied by an increase in pressure or potential energy. This principle is based on the conservation of energy in fluid flow.
Can you explain the Principle of Continuity and its connection to fluid flow?
The Principle of Continuity states that the mass flow rate of an incompressible fluid remains constant along a streamline, provided there are no sources or sinks within the flow. This principle is based on the conservation of mass and is often used in conjunction with Bernoulli’s Principle to analyze fluid flow in pipes and channels.
How does the Venturi Tube demonstrate Bernoulli’s Principle in action?
The Venturi Tube is a device used to measure the flow velocity of a fluid. It consists of a converging section, a throat, and a diverging section. According to Bernoulli’s Principle, as the fluid flows through the converging section, its velocity increases, resulting in a decrease in pressure. Conversely, in the diverging section, where the velocity decreases, the pressure increases. This pressure difference can be measured and used to calculate the fluid velocity.
What role does the conservation of energy play in understanding fluid flow at constant depth?
At constant depth, the total energy of a fluid remains constant along a streamline, as long as no energy is added to or removed from the system. This principle is based on the conservation of mechanical energy, which includes kinetic energy (due to fluid velocity), potential energy (due to fluid elevation), and pressure energy (due to fluid pressure). Changes in one form of energy are compensated by corresponding changes in the other forms, maintaining total energy conservation.
What is Bernoulli’s equation for static fluids, and how is it derived?
Bernoulli’s equation for static fluids, also known as the steady-flow energy equation, states that the total energy per unit mass of a fluid remains constant along a streamline. It is derived by applying the principle of conservation of energy to a fluid element with no sources or sinks within the flow, resulting in an expression that relates the fluid’s velocity, pressure, and elevation along the streamline.
How does Bernoulli’s equation relate to the flow of fluids in pipes and channels?
In pipes and channels, Bernoulli’s equation can be used to analyze the behavior of fluids and predict changes in velocity, pressure, and elevation along the flow path. By considering the effects of pipe diameter, flow rate, and fluid properties, engineers can design systems that optimize energy efficiency, minimize pressure losses, and meet specific performance requirements.
Are there any limitations or assumptions associated with the application of Bernoulli’s equation in real-world fluid flow scenarios?
Yes, Bernoulli’s equation is based on several assumptions, including steady, incompressible flow with no friction or viscosity effects, and no sources or sinks within the flow. In real-world scenarios, these assumptions may not hold, leading to deviations from the predicted behavior. Additionally, Bernoulli’s equation does not account for changes in flow direction, turbulence, or boundary effects, which can affect its accuracy in certain applications.