Beta Decay

The discovery of beta decay traces back to the late 19th century. In 1899, Ernest Rutherford, a pioneering physicist in radioactivity, observed that some elements emitted radiation that could penetrate metal foils and fog photographic plates. This was different from alpha radiation, which he had already characterized.

Rutherford named this new radiation “beta rays,” after the second letter of the Greek alphabet because it was the second type of radiation he had discovered (alpha rays being the first). He found that beta rays were much more penetrating than alpha rays and were high-speed electrons ejected from the nucleus of an atom.

Further studies by other scientists, including James Chadwick and Niels Bohr, expanded on Rutherford’s findings. They explored the properties of beta radiation and its implications for atomic structure. It was eventually understood that beta decay was a process where an unstable atomic nucleus transforms into a more stable one by emitting a beta particle, an electron, or its antiparticle, a positron.

What is Beta Decay?

It’s a type of radioactive decay where a beta particle (an electron or a positron) is emitted from an atomic nucleus. This process changes the original nucleus into an atom with a different number of protons. Beta decay is a fascinating process that occurs at the atomic level. It’s one of the ways that an unstable atom can become more stable. In physics, stability often means having a balanced ratio of protons to neutrons in the nucleus, and beta decay is a process that helps achieve this balance.

Inside the nucleus of an atom, you have protons and neutrons. Protons are positively charged, while neutrons have no charge.
Sometimes, there are too many neutrons in the nucleus for it to be stable. To fix this imbalance, one of the neutrons can transform into a proton.

When this transformation happens, the neutron doesn’t just turn into a proton; it also releases a particle called a beta particle, which is essentially an electron. This electron is ejected from the nucleus at high speed, which is why we call it beta radiation.

Beta decay significantly affects the overall stability of an atom by altering the ratio of protons to neutrons in the nucleus. Here’s how it contributes to stability:

Atoms are most stable when they have the right balance of neutrons to protons. If there are too many or too few neutrons relative to protons, the atom is unstable and radioactive. Beta decay helps adjust this neutron-to-proton ratio. In beta-minus decay, a neutron turns into a proton, decreasing the number of neutrons and increasing the number of protons. Conversely, in beta-plus decay, a proton is converted into a neutron, increasing neutrons and reducing protons.

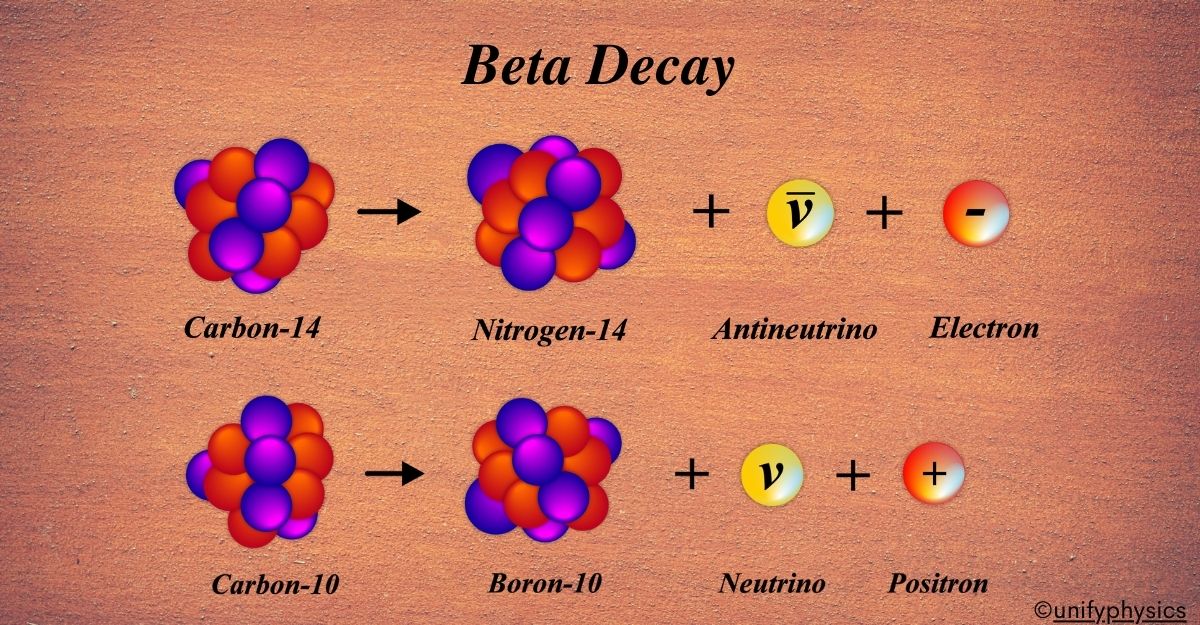
This transformation can change one element into another on the periodic table. For example, Carbon-14 (6 protons, 8 neutrons) decays into Nitrogen-14 (7 protons, 7 neutrons) through beta-minus decay. The process releases energy in the form of the kinetic energy of the emitted beta particle and an accompanying neutrino. This release of energy also contributes to the atom reaching a more stable state.

In simple terms, beta decay is like a self-correcting mechanism for an atom’s nucleus. By emitting a beta particle, the nucleus can adjust its composition from having too many neutrons to having a more stable balance of protons and neutrons.

Types of Beta Decay

Beta-Minus Decay (β⁻)

A neutron is transformed into a proton, and an electron (beta particle) and an antineutrino are emitted. Beta-minus decay (β⁻ decay) is one of the two main types of beta decay. It’s a process that occurs in certain unstable atoms where there are more neutrons than necessary for stability. Here’s what happens during β⁻ decay:

A neutron in the nucleus, which is neutral, transforms into a proton, which has a positive charge. This transformation isn’t just a simple switch; it also results in the creation of two very small particles:

• An electron is negatively charged and is what we call the beta particle in this type of decay.
• An antineutrino is a neutral particle with almost no mass and rarely interacts with matter.

The outcome of β⁻ decay is that the atomic number of the atom increases by one because there’s now one more proton in the nucleus. However, the mass number stays the same because a neutron has been lost, but a proton has been gained, and they have nearly the same mass.

For example, consider an atom of Carbon-14. It has 6 protons and 8 neutrons. When it undergoes β⁻ decay, one of its neutrons turns into a proton, resulting in an atom of Nitrogen-14, which has 7 protons and 7 neutrons. This process helps the atom move towards stability by correcting the imbalance between protons and neutrons. It’s a natural and spontaneous process that plays a key role in the radioactive decay series of many elements.

The basic reaction for β⁻ decay

\(\displaystyle n \rightarrow p^+ + e^- + \bar{\nu}_e \)

• (n) is a neutron
• (p⁺) is a proton
• (e^–) is the emitted beta particle (electron)
• (\(\displaystyle \bar{\nu}_e\)) is the antineutrino

In terms of atomic numbers and mass numbers, the decay can be represented as:

\(\displaystyle Z^AX_N \rightarrow {Z+1}^AX_{N-1} + e^- + \bar{\nu}_e \)

• (\(\displaystyle _Z^AX_N \)) is the parent nucleus with atomic number (Z ) and neutron number (N)
• (\(\displaystyle {Z+1}^AX{N-1} \)) is the daughter nucleus
• (A) is the mass number (protons + neutrons), which remains constant
• (Z) increases by 1 because a neutron has turned into a proton

This equation shows that in β⁻ decay, the parent nucleus emits an electron and an antineutrino, resulting in a daughter nucleus with one more proton and one less neutron, thus increasing the atomic number by one while keeping the mass number unchanged.

Beta-Minus Decay (β⁻) Example: Consider the isotope Carbon-14, which has an excess of neutrons. It undergoes β⁻ decay to become more stable:

\(\displaystyle _6^{14}\text{C} \rightarrow _7^{14}\text{N} + e^- + \bar{\nu}_e \)

A neutron in Carbon-14 is converted into a proton. An electron (e^–), also known as a beta particle, is emitted. An antineutrino (\(\displaystyle\bar{\nu}_e\)) is also emitted, carrying away some energy and momentum. After the decay, we get Nitrogen-14, which has 7 protons and 7 neutrons. The atomic number increases by one, but the mass number remains the same.

Beta-Plus Decay (β⁺)

A proton is converted into a neutron, releasing a positron (the electron’s antiparticle) and a neutrino. Beta-plus decay (β⁺ decay) is a type of beta decay where a proton in an atom’s nucleus is transformed into a neutron. This process is less common than beta-minus decay and occurs in proton-rich nuclei that are unstable and need to increase their neutron-to-proton ratio to become more stable. Here’s what happens during β⁺ decay:

A proton, which is positively charged, changes into a neutron, which has no charge. This transformation also produces two particles: A positron is the antimatter counterpart of an electron and has a positive charge. A neutrino is a very light particle that rarely interacts with matter.

The outcome of β⁺ decay is that the atomic number of the atom decreases by one because there’s now one less proton in the nucleus. However, the mass number remains the same because a proton has been lost, but a neutron has been gained, and they have nearly the same mass.

For example, consider an atom of Nitrogen-13. It has 7 protons and 6 neutrons. When it undergoes β⁺ decay, one of its protons turns into a neutron, resulting in an atom of Carbon-13, which has 6 protons and 7 neutrons. This process helps the atom move toward stability by correcting the imbalance between protons and neutrons.

In Beta-Plus Decay (β⁺), we can derive an expression to represent the process. Here’s a simplified version suitable for 12th-grade physics students:

Let’s start with the basic reaction for β⁺ decay:

\(\displaystyle p^+ \rightarrow n + e^+ + \nu_e \)

• (p⁺) is a proton
• (n) is a neutron
• (e⁺) is the emitted positron (the antimatter counterpart of an electron)
• (\(\displaystyle\nu_e\)) is the neutrino

In terms of atomic numbers and mass numbers, the decay can be represented as:

\(\displaystyle Z^AX_N \rightarrow {Z-1}^AX_{N+1} + e^+ + \nu_e \)

• (\(\displaystyle _Z^AX_N \)) is the parent nucleus with atomic number ( Z ) and neutron number ( N )
• (\(\displaystyle {Z-1}^AX{N+1}\)) is the daughter nucleus
• (A) is the mass number (protons + neutrons), which remains constant
• (Z) decreases by 1 because a proton has turned into a neutron

Beta-Plus Decay (β⁺) Example: Consider the isotope Nitrogen-13, which has an excess of protons. It undergoes β⁺ decay to become more stable:

\(\displaystyle _7^{13}\text{N} \rightarrow _6^{13}\text{C} + e^+ + \nu_e \)

A proton in Nitrogen-13 is converted into a neutron. A positron (e⁺) is emitted, which is the antiparticle of an electron. A neutrino (\(\displaystyle\nu_e\)) is also emitted, carrying away some energy and momentum. After the decay, we get Carbon-13, which has 6 protons and 7 neutrons. The atomic number decreases by one, but the mass number remains the same.

This equation shows that in β⁺ decay, the parent nucleus emits a positron and a neutrino, resulting in a daughter nucleus with one less proton and one more neutron, thus decreasing the atomic number by one while keeping the mass number unchanged.

If an atom undergoes multiple consecutive Beta-Plus Decays (β⁺), it will continue to transform by converting protons into neutrons, emitting positrons and neutrinos with each decay. With each β⁺ decay, the atomic number decreases by one because a proton is lost and a neutron is gained.

The mass number stays the same because the total number of nucleons (protons and neutrons) doesn’t change. Since the atomic number defines the element, each β⁺ decay changes the identity of the atom to a new element that is one place lower on the periodic table.

The atom undergoes β⁺ decay to achieve a more stable neutron-to-proton ratio. If multiple decays occur, it indicates that the atom is trying to reach a stable state through successive transformations. Each decay releases energy in the form of kinetic energy of the emitted positron and neutrino, as well as any gamma radiation if the daughter nucleus is in an excited state.

For example, if an isotope undergoes two consecutive β⁺ decays, it would look like this:

\(\displaystyle Z^AX_N \rightarrow {Z-1}^AX_{N+1} + e^+ + \nu_e \)

\(\displaystyle {Z-1}^AX{N+1} \rightarrow {Z-2}^AX{N+2} + e^+ + \nu_e \)

This shows that after two β⁺ decays, the atomic number has decreased by two, but the mass number remains unchanged. The number of Beta-Plus Decays (β⁺) an atom can undergo is limited by several factors:

An atom must be proton-rich to undergo β⁺ decay. Once it reaches a balanced neutron-to-proton ratio, it will no longer decay via this process. The decay process seeks to achieve a stable nucleus. Once stability is reached, further β⁺ decays are not necessary and do not occur.

Each β⁺ decay requires sufficient energy to occur. If the resulting nucleus does not have enough energy to allow another proton to convert into a neutron, further β⁺ decay will not happen. The binding energy of the nucleus also plays a role. If the binding energy per nucleon increases with each decay, it indicates a move toward stability, and the decay will continue until this energy is maximized.

An atom cannot decay via β⁺ beyond hydrogen-1 (protium), as it would result in a neutron, which is not bound within a nucleus and will decay via beta-minus decay if free. In practice, most atoms will undergo only a few β⁺ decays before reaching a stable state or before other decay modes become more favorable.

Electron Capture

An alternative to β⁺ decay is where an inner orbital electron is captured by the nucleus, transforming a proton into a neutron and emitting a neutrino. Electron Capture is a process where an unstable atom’s nucleus captures one of its electrons, usually from the closest shell to the nucleus (the K-shell). This process occurs when the nucleus contains too many protons to be stable.

An electron from the innermost orbital merges with a proton in the nucleus, transforming that proton into a neutron. As a result of this reaction, a neutrino is emitted from the nucleus.

The equation for electron capture can be written as:

\(\displaystyle p^+ + e^- \rightarrow n + \nu_e \)

In terms of atomic numbers and mass numbers, the decay can be represented as:

\(\displaystyle Z^AX_N + e^- \rightarrow {Z-1}^AX_{N+1} + \nu_e \)

After electron capture, the atomic number decreases by one because a proton has been converted into a neutron, but the mass number remains unchanged because the total number of nucleons stays the same. An example of electron capture is when Potassium-40 captures an electron and becomes Argon-40:

\(\displaystyle {19}^{40}\text{K} + e^- \rightarrow {18}^{40}\text{Ar} + \nu_e \)

This process helps the atom achieve a more stable state by reducing its proton count without changing its mass number.

How does electron capture differ from beta decay?

Electron capture and beta decay are both processes that unstable atoms can undergo to achieve a more stable state, but they differ in several key ways:

An inner orbital electron is captured by the nucleus, where it combines with a proton to form a neutron and emits a neutrino.
In beta-minus decay, a neutron is transformed into a proton, emitting an electron and an antineutrino. In beta-plus decay, a proton is transformed into a neutron, emitting a positron and a neutrino.

Only a neutrino is emitted. Beta particles (electrons or positrons) are emitted along with neutrinos or antineutrinos. Both processes decrease the atomic number by one, but in electron capture, this happens by the absorption of an electron, while in beta decay, it happens by the emission of a beta particle.

Generally involves less energy release compared to beta decay because no beta particle is emitted. Usually involves more energy release due to the emission of beta particles and neutrinos.

More likely to occur in proton-rich nuclei where there’s insufficient energy to allow for positron emission (beta-plus decay). Occurs in neutron-rich nuclei (beta-minus decay) or proton-rich nuclei with sufficient energy for positron emission (beta-plus decay).

Both processes lead to a decrease in the atomic number by one, electron capture involves the absorption of an electron and emission of only a neutrino, whereas beta decay involves the transformation of nucleons and emission of beta particles along with neutrinos.

What is Neutrino?

In beta decay, neutrinos are fundamental particles released alongside beta particles. They carry away energy and momentum but have no charge and very little mass. A neutrino is a fundamental particle in physics, similar to an electron but with some key differences.

Neutrinos are electrically neutral, meaning they have no charge. This is different from electrons, which have a negative charge.
Neutrinos have an incredibly small mass, so small that it was once thought they were massless. Their mass is much less than that of electrons.

Neutrinos interact very weakly with other matter. This means they can pass through almost anything without being stopped or detected, which is why they are often called “ghost particles.” There are three types (flavors) of neutrinos: electron neutrinos (\(\displaystyle\nu_e\)), muon neutrinos (\(\displaystyle\nu_\mu\)), and tau neutrinos (\(\displaystyle\nu_\tau\)). Each type is associated with a corresponding charged particle (electron, muon, and tau).

Neutrinos are produced in various nuclear reactions, such as during the fusion processes in the sun, radioactive decay (like beta decay), and when cosmic rays hit atoms in the Earth’s atmosphere. In beta decay and electron capture, neutrinos carry away excess energy and help conserve momentum and angular momentum in the reaction.

Fermi’s Theory of Beta Decay

Proposed by Enrico Fermi in 1934, it explains beta decay as a four-fermion interaction, which was later incorporated into the electroweak interaction theories. Fermi’s Theory of Beta Decay is a fundamental concept in nuclear physics that explains how and why beta decay occurs at the subatomic level.

Beta decay is a process where an unstable nucleus emits a beta particle (an electron or positron) to become more stable. Enrico Fermi, an Italian physicist, developed a theory in 1934 to describe this process. He proposed that beta decay could be explained by the weak force, one of the four fundamental forces in nature.

The weak force is responsible for the transformation of one type of subatomic particle into another. In beta decay, it converts neutrons into protons or vice versa. Fermi’s theory also introduced the concept of the neutrino, a neutral particle emitted alongside the beta particle to conserve energy, momentum, and angular momentum in the decay process.

The theory involves four fermions (particles that make up matter): a neutron or proton in the nucleus, an electron or positron emitted, and a neutrino or antineutrino. According to Fermi’s theory, during beta decay, a neutron turns into a proton through the weak force, emitting an electron and an antineutrino; or a proton turns into a neutron, emitting a positron and a neutrino.

Consider a neutron decaying into a proton, an electron, and an antineutrino. The total energy before decay must equal the total energy after decay. If we denote the initial energy of the neutron as (E_n), and the energies of the proton, electron, and antineutrino as (E_p), (E_e), and (E_ν) respectively, then:

\(\displaystyle E_n = E_p + E_e + E_{\nu} \)

Similarly, the total momentum must be conserved. If we denote the initial momentum of the neutron as (p_n), and the momenta of the proton, electron, and antineutrino as (p_p), (p_e), and (p_ν) respectively, then:

\(\displaystyle p_n = p_p + p_e + p_{\nu} \)

Fermi’s theory uses this rule to calculate the probability per unit time that a certain transition will occur, which is proportional to the square of the matrix element (M) and the density of final states ρ(E):

\(\displaystyle W = G_F^2 |M|^2 \rho(E) \)

• (W) is the transition rate,
• (G_F) is the Fermi coupling constant,
• (|M|²) is the square of the matrix element,
• ρ(E) is the density of final states.

The density of final states can be related to the energy distribution of emitted electrons, leading to a spectrum that can be measured experimentally. The matrix element involves complex calculations related to quantum mechanics and includes factors like spin states and overlap between initial and final wave functions.

Fermi’s Theory was groundbreaking because it provided a quantitative description of beta decay and predicted the existence of neutrinos before they were directly detected.

Application and Importance

Beta decay is a crucial process in nuclear physics with several important applications:

• Dating Techniques: Beta decay is used in radiocarbon dating, which is a method to determine the age of ancient artifacts. Carbon-14, a radioactive isotope, decays over time, and by measuring the remaining amount, scientists can estimate the age of an object.
• Medical Applications: Radioisotopes that undergo beta decay are used in medical diagnostics and treatments. For example, Strontium-90 is used in radiotherapy to treat eye diseases and bone cancer.
• Nuclear Batteries: Beta-emitting isotopes can be used in radioisotope thermoelectric generators (RTGs) to provide long-lasting power sources for spacecraft and remote devices.
• Understanding Fundamental Physics: Studying beta decay helps physicists understand the weak force, one of the four fundamental forces in nature, and the behavior of subatomic particles.
• Safety and Environment: Knowledge of beta decay is important for managing nuclear waste and understanding environmental radiation.

The study of beta decay is essential not only for its practical applications but also for enhancing our understanding of the universe at the most fundamental level.

Also Read: Alpha Decay

Solved Examples

Problem 1: Write the equation for the beta-minus decay of Carbon-14.

Solution: In beta-minus (\(\displaystyle\beta^- \)) decay, a neutron in the nucleus converts into a proton, emitting an electron (beta particle) and an antineutrino. The atomic number increases by 1, but the mass number remains the same.

For Carbon-14 (\(\displaystyle ^{14}_{6}\text{C} \)):

\(\displaystyle ^{14}_{6}\text{C} \rightarrow ^{14}_{7}\text{N} + e^- + \bar{\nu}_e \)

The beta-minus decay equation for Carbon-14 is:

\(\displaystyle ^{14}_{6}\text{C} \rightarrow ^{14}_{7}\text{N} + e^- + \bar{\nu}_e \)

Problem 2: Write the equation for the beta-plus decay of Sodium-22.

Solution: In beta-plus (\(\displaystyle \beta^+ \)) decay, a proton in the nucleus converts into a neutron, emitting a positron (positive beta particle) and a neutrino. The atomic number decreases by 1, but the mass number remains the same.

For Sodium-22 (\(\displaystyle ^{22}_{11}\text{Na} \)):

\(\displaystyle ^{22}_{11}\text{Na} \rightarrow ^{22}_{10}\text{Ne} + e^+ + \nu_e \)

The beta-plus decay equation for Sodium-22 is:

\(\displaystyle ^{22}_{11}\text{Na} \rightarrow ^{22}_{10}\text{Ne} + e^+ + \nu_e \)

Problem 3: Write the equation for the electron capture by Beryllium-7.

Solution: In electron capture, an inner orbital electron is captured by the nucleus and combines with a proton to form a neutron, emitting a neutrino. The atomic number decreases by 1, but the mass number remains the same.

For Beryllium-7 (\(\displaystyle ^{7}_{4}\text{Be} \)):

\(\displaystyle ^{7}_{4}\text{Be} + e^- \rightarrow ^{7}_{3}\text{Li} + \nu_e \)

The electron capture equation for Beryllium-7 is:

\(\displaystyle ^{7}_{4}\text{Be} + e^- \rightarrow ^{7}_{3}\text{Li} + \nu_e \)

Problem 4: In the beta-minus decay of Phosphorus-32, calculate the maximum kinetic energy of the emitted electron if the Q value of the decay is 1.71 MeV. Assume the neutrino carries away negligible energy.

Solution: In beta-minus decay, the Q value is shared between the electron and the neutrino. If the neutrino carries away negligible energy, the electron gets almost all the energy.

Given: \(\displaystyle Q = 1.71 \, \text{MeV} \)

Since the neutrino carries negligible energy:

\(\displaystyle K_e \approx Q = 1.71 \, \text{MeV} \)

The maximum kinetic energy of the emitted electron is approximately 1.71 MeV.

Problem 5: Using Fermi’s theory of beta decay, calculate the lifetime of a neutron given the following data: the phase space factor (f) is 1, and the matrix element (\(\displaystyle |M|^2 \)) is 1. Assume a simplified scenario where the decay constant (\(\displaystyle \lambda \)) is 1.

Solution: Fermi’s theory of beta decay relates the decay constant (\(\displaystyle \lambda \)) to the phase space factor (f) and the matrix element (\(\displaystyle |M|^2 \)) by:

\(\displaystyle \lambda = \frac{G^2 |M|^2 f}{2\pi^3 \hbar^7} \)

Given: f = 1 , \(\displaystyle |M|^2 = 1 \), \(\displaystyle \lambda = 1 \)

The lifetime ( \(\displaystyle\tau \)) is the inverse of the decay constant:

\(\displaystyle \tau = \frac{1}{\lambda} \)

Given the simplified scenario where the decay constant (\(\displaystyle \lambda \)) is 1, the lifetime ( \(\displaystyle\tau \)) of the neutron is:

\(\displaystyle \tau = 1 \, \text{s} \)

Problem 6: Calculate the threshold energy required for beta-plus decay of Fluorine-18 if the mass of Fluorine-18 is 18.000937 u and the mass of Oxygen-18 is 17.999160 u. The mass of an electron is 0.000548 u.

Solution: The threshold energy for beta-plus decay is the energy required to convert a proton into a neutron, positron, and neutrino. This energy must come from the mass difference between the parent and daughter nuclei.

Given:

• Mass of (\(\displaystyle ^{18}_{9}\text{F} \): \( 18.000937 \, \text{u} \))
• Mass of (\(\displaystyle ^{18}_{8}\text{O} \): \( 17.999160 \, \text{u} \))
• Mass of electron: ( 0.000548 u)

The threshold energy (Q) is:

\(\displaystyle Q = (m_{\text{F}} – m_{\text{O}} – 2m_e)c^2 \)

Convert the mass difference to energy (1 u = 931.5 MeV):

\(\displaystyle m_{\text{F}} = 18.000937 \, \text{u} \)

\(\displaystyle m_{\text{O}} = 17.999160 \, \text{u} \)

\(\displaystyle m_e = 0.000548 \, \text{u} \)

Calculate the mass difference:

\(\displaystyle \Delta m = 18.000937 – 17.999160 – 2 \times 0.000548 \)

\(\displaystyle\Delta m = 18.000937 – 17.999160 – 0.001096 \)

\(\displaystyle \Delta m = 0.000681 \, \text{u} \)

Convert the mass difference to energy:

\(\displaystyle Q = 0.000681 \, \text{u} \times 931.5 \, \text{MeV/u} \)

\(\displaystyle Q \approx 0.634 \, \text{MeV} \)

The threshold energy required for the beta-plus decay of Fluorine-18 is approximately 0.634 MeV.

FAQs