The story of gravity begins in ancient times. Greek philosopher Aristotle believed that objects fell towards the Earth due to their nature. However, his ideas were challenged and built upon over centuries.
Fast forward to the Middle Ages, when scholars like John Philoponus in Byzantium and Brahmagupta in India began to see gravity as an attracting force, a revolutionary idea for the time.
The Renaissance brought a flurry of scientific thought. Galileo Galilei made a groundbreaking discovery: objects, regardless of their mass, fall at the same rate in the absence of air resistance. This was a significant step towards understanding gravitational acceleration.
Then came Sir Isaac Newton in the 17th century, who introduced the Universal Law of Gravitation. He proposed that every mass exerts an attractive force on every other mass. The strength of this force is directly proportional to the product of the two masses and inversely proportional to the square of the distance between them.
In the late 18th century, Henry Cavendish performed meticulous experiments to measure the force of gravity between masses and determined the value of the gravitational constant G, which is crucial for calculating gravitational field intensity.
In the early 20th century, Albert Einstein changed the game with his theory of general relativity. He described gravity not as a force, but as a curvature of spacetime caused by mass and energy.
Today, scientists continue to explore the nature of gravity through advanced theories like quantum gravity and string theory, hoping to uncover a more fundamental understanding of the force that governs the cosmos.
What is a Gravitational Field?
A gravitational field is an invisible region around a mass where another mass experiences a force of attraction. It’s like a field of influence that extends around every object with mass.
Imagine you’re at a park, and there’s a large round trampoline with a heavy ball in the center. This ball creates a dip in the trampoline’s fabric. Now, if you roll a smaller ball onto the trampoline, it will naturally move towards the larger ball, following the curve of the dip. This is similar to how a gravitational field works.
In physics, a gravitational field is like that dip in the trampoline created by a mass (like a heavy ball). It’s an invisible force field that surrounds any object that has mass. The field represents the ability of the mass to attract other masses towards it. The strength of this field depends on the amount of mass and the distance from the mass creating the field.
- Every object with mass, from a tiny pebble to a giant planet, has a gravitational field around it.
- This field extends out into space in all directions, and its strength decreases as you move away from the object.
- If you place another object with mass in this field, it will feel a force pulling it towards the first object. This force is what we experience as gravity.
In simple terms, a gravitational field is a region around a mass where other masses feel an attractive force. The field is stronger closer to the mass and weaker further away. It’s this field that keeps our feet on the ground, the moon orbiting the Earth, and the planets orbiting the Sun.
So, a gravitational field is the way we describe how objects with mass influence the space around them, causing other objects to be attracted to them. It’s an essential concept that helps us understand the very nature of how things move and interact in our universe.
What is Gravitational Field Intensity?
Gravitational field intensity, often denoted by Eg, is the force experienced by a unit mass placed in a gravitational field. It’s a vector quantity, meaning it has both magnitude and direction.
Imagine you’re standing on a trampoline. The trampoline fabric stretches and creates a dip where you’re standing. Now, if a friend throws a ball onto the trampoline, it will roll towards you, right into the dip. This is similar to how a gravitational field works. The trampoline fabric represents the gravitational field around you, and the ball is attracted to the dip, just like objects are attracted to each other by gravity.
- Gravitational Field Intensity (Eg) is a measure of how strong the gravitational pull is at a particular point in space.
- It’s like the “strength” of the dip in the trampoline. The deeper the dip, the stronger the pull.
- Mathematically, we define (Eg) as the force of gravity acting on a unit mass at a point in the gravitational field. If you had 1 kilogram of mass, (Eg) tells you how much force would be pulling on that 1 kilogram.
- It’s a vector quantity, which means it has both magnitude (how strong) and direction (where it’s pulling towards).
To put it in formula terms, if you have a mass (M) creating a gravitational field, the intensity (Eg) at a distance (r) from the mass is given by:
\(\displaystyle E_g = -\frac{G \cdot M}{r^2} \)
So, Gravitational Field Intensity is essentially the “strength” of gravity at a point, and it’s what causes objects to move toward each other in space. It’s why planets orbit stars, moons orbit planets, and why we don’t float off into space from the Earth’s surface. It’s a fundamental force that’s all about attraction!
The negative sign in the equation indicates that the gravitational field intensity vector points towards the mass (M). It’s a way to show that the force of gravity is attractive, pulling objects in and not pushing them away. This is crucial in understanding the nature of gravity as an attractive force that acts to pull objects together.
Unit of Gravitational Field Intensity: The unit of Gravitational Field Intensity is Newton per kilogram (N/kg).
This unit tells us how many Newtons of force would act on each kilogram of mass in a gravitational field.
Dimensional Formula: The dimensional formula of Gravitational Field Intensity is [M0L1T-2].
Gravitational Field Intensity of a Point Mass
Imagine you’re standing on a hill with a ball. If you let go of the ball, it rolls down the hill towards the bottom. This happens because Earth’s gravity is pulling on the ball. Now, if we want to measure how strong this pull is at any point around the ball, we’re talking about the gravitational field intensity.
Suppose a particle of mass M is placed at point O and a second particle of mass m is placed at point A. Let OA = r. The mass M creates a field \(\displaystyle \overrightarrow{E} \) at the side of mass m and this field exerts a force

Gravitational field intensity tells us how much force is acting on a unit mass (like 1 kilogram) at a certain point in the gravitational field created by a mass (like the Earth or the ball).
- Gravitational Field Intensity (Eg): It’s a measure of the gravitational force per unit mass at a point in space due to a point mass.
- Point Mass: This is an object with mass that’s so small compared to the distances we’re considering that we can think of it as a single point in space.
The formula for (Eg) of a point mass (M) at a distance (r) is:
\(\displaystyle E_g = -\frac{G \cdot M}{r^2} \)
- (G) is the gravitational constant, a number that tells us how strong gravity is in the universe.
- (M) is the mass of the object creating the gravitational field.
- (r) is the distance from the center of the mass to the point where we’re measuring (Eg).
The negative sign in the formula is important. It tells us that the gravitational field intensity is directed towards the mass creating the field. This is because gravity is always an attractive force—it pulls things together, it doesn’t push them apart.
If you’re standing on that hill with a ball, the gravitational field intensity at the point where the ball is would be a vector pointing straight down towards the center of the Earth. It’s this gravitational field intensity that causes the ball to roll down the hill when you let it go.
Gravitational field intensity is a way to describe how strong gravity is at a particular point in space, and it’s a fundamental concept that helps us understand why objects move the way they do under the influence of gravity.
Newton’s law of universal gravitation states that the force of gravity (F) between two masses (M) and (m) is:
\(\displaystyle F = G \cdot \frac{M \cdot m}{r^2} \)
Here, (G) is the gravitational constant, (M) is the mass of the point mass, (m) is the mass of the object experiencing the force, and (r) is the distance between the centers of the two masses.
Gravitational Field Intensity is the force experienced by a unit mass placed in a gravitational field. So, if we divide the force (F) by the mass (m) that’s feeling the force, we get:
\(\displaystyle E_g = \frac{F}{m} \)
Replace (F) in the equation above with the expression from Newton’s Law of Universal Gravitation:
\(\displaystyle E_g = \frac{G \cdot \frac{M \cdot m}{r^2}}{m} \)
The mass (m) appears in both the numerator and the denominator, so it cancels out:
\(\displaystyle E_g = \frac{G \cdot M}{r^2} \)
Gravitational force is always attractive, pulling objects toward the mass creating the field. To represent this direction towards the mass, we include a negative sign:
\(\displaystyle E_g = -\frac{G \cdot M}{r^2} \)
And there we have it! The expression for the Gravitational Field Intensity (Eg) of a point mass (M) at a distance (r) is:
\(\displaystyle E_g = -\frac{G \cdot M}{r^2} \)
The negative sign indicates that the gravitational field intensity vector points towards the mass (M), showing the direction of the attractive force.
Gravitational Field Intensity Resulting from a Ring
Consider a ring of mass (M) and radius (R). We want to find the gravitational field intensity at a point on the axis of the ring, a distance (x) from its center. Take a small element of the ring with mass (dm). The gravitational field intensity due to this element at the point is (dEg), which is directed towards the element.
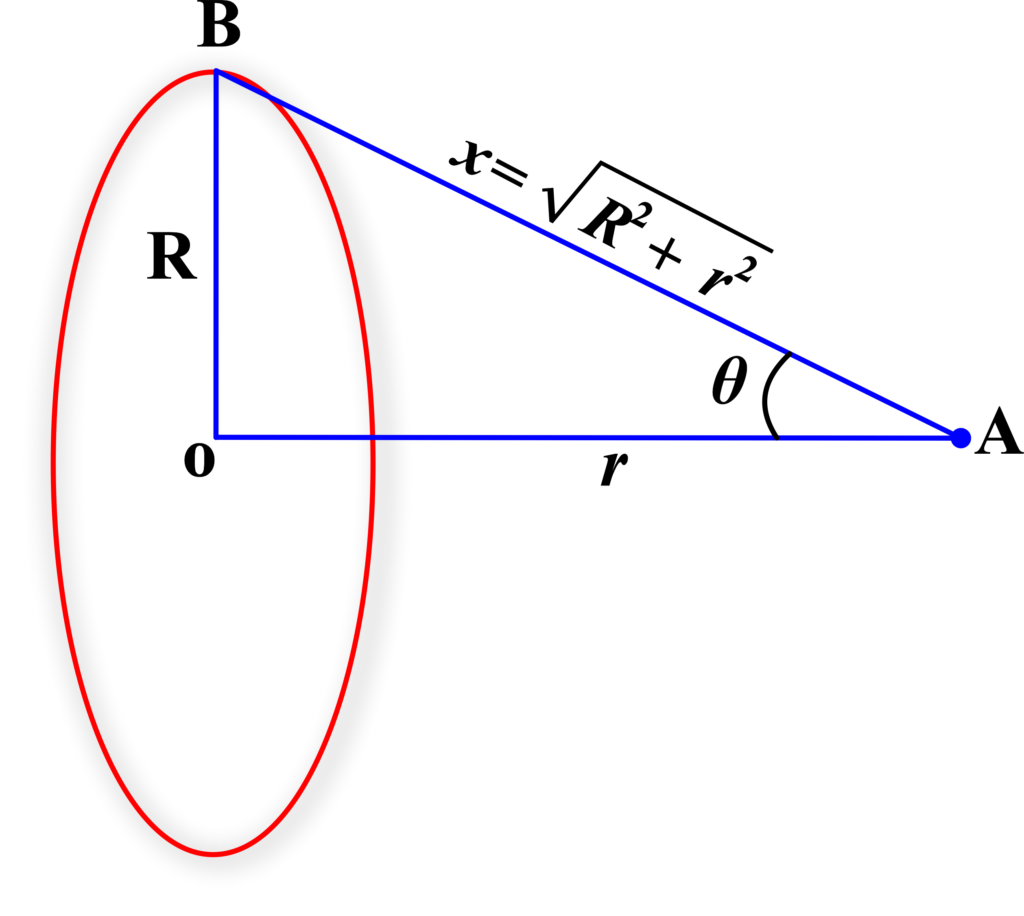
The distance from the point to the element is (r), which can be found using the Pythagorean theorem since (r) is the hypotenuse of a right triangle with sides (x) and (R). The gravitational field intensity due to the element (dm) is given by:
\(\displaystyle dE_g = \frac{G \cdot dm}{r^2} \)
The intensity (dEg) has two components: one along the axis of the ring and one perpendicular to it. By symmetry, the perpendicular components cancel out, leaving only the axial component. The axial component of (dEg) is
\(\displaystyle dE_{g_{axial}} = dE_g \cdot \cos(\theta) \)
where (θ) is the angle between (r) and the axis. Using the triangle mentioned earlier, ( \(\displaystyle\cos(\theta) = \frac{x}{r}\) ).
To find the total gravitational field intensity, integrate the axial component over the entire ring:
\(\displaystyle E_g = \int dE_{g_{axial}} = \int \frac{G \cdot dm}{r^2} \cdot \frac{x}{r} \)
Replace (r) with (\(\displaystyle \sqrt{R^2 + x^2} \)) in the integral. Since the mass distribution is uniform, integrate (dm) over the entire ring to get (M).
After integrating, the expression for the gravitational field intensity due to the ring is:
\(\displaystyle E_g = -\frac{G \cdot M \cdot x}{(R^2 + x^2)^{3/2}} \)
This derivation shows that the gravitational field intensity due to a ring decreases with distance from the ring and depends on both the mass of the ring and the distance from the point to the ring’s center.
Gravitational Field Resulting from a Uniform Spherical Shell
(i) Outside the Spherical Shell:
The field intensity is the same as if the entire mass of the shell were concentrated at its center. Imagine you have a thin, hollow ball, like a basketball shell, with a uniform mass distribution. We want to know the gravitational field intensity (Eg) at a point outside this shell.
Consider a spherical shell with mass (M) and radius (R). The shell is uniform, meaning the mass is spread out evenly over its surface. We’re interested in finding (Eg) at a point that’s a distance (r) from the center of the shell, where (r > R).
A key concept here is the shell theorem. It tells us that the gravitational field outside a uniform spherical shell is the same as if all the shell’s mass were concentrated at its center. The gravitational field intensity at our point of interest is given by the formula:
\(\displaystyle E_g = -\frac{G \cdot M}{r^2} \)
The negative sign in the formula indicates that (Eg) is directed towards the center of the spherical shell. This aligns with the fact that gravity is an attractive force.
So, for a student standing outside a spherical shell, the gravitational pull they’d feel would be as if the entire mass of the shell were at a single point at its center. This makes calculations much simpler because you don’t have to worry about the shell’s thickness or what part of the shell is pulling more—every part pulls together as if it were all at the center.
(ii) On the Surface of the Spherical Shell:
Consider a spherical shell with a uniform mass distribution, having a total mass (M) and radius (R). We want to calculate the gravitational field intensity (Eg) at a point that lies on the surface of the shell.
According to the shell theorem, the gravitational field intensity at a point on the surface of a uniform spherical shell is the same as if the entire mass of the shell were concentrated at its center.
Based on Newton’s law of gravitation, the gravitational field intensity at a distance ( R ) (the radius of the shell) from a point mass (M) is given by:
\(\displaystyle E_g = -\frac{G \cdot M}{R^2} \)
Here, (G) is the gravitational constant, and the negative sign indicates that the gravitational field intensity is directed towards the center of the mass creating the field.
Since we are considering a point on the surface, the distance (r) is equal to the radius (R) of the spherical shell. Therefore, the gravitational field intensity (Eg) at a point on the surface of a uniform spherical shell is:
\(\displaystyle E_g = -\frac{G \cdot M}{R^2} \)
This expression tells us that the gravitational field intensity on the surface of a spherical shell is directed towards the center of the shell and is a constant value for all points on the surface. The derivation is straightforward because of the shell theorem, which simplifies the complex reality of distributed mass into a point mass at the center for points on the surface.
(iii) Inside the Spherical Shell:
We’re interested in finding the gravitational field intensity (Eg) at a point inside this shell, which means any point that is at a distance (r < R) from the center.
Gauss’s law for gravity states that the gravitational flux through a closed surface is proportional to the enclosed mass. Since there’s no mass inside a hollow shell, the net flux is zero.
If the net flux is zero, this implies that the gravitational field intensity (Eg) must also be zero everywhere inside the shell. Since (Eg) is zero, there’s no direction to assign, and thus no negative sign is needed.
Therefore, the gravitational field intensity (Eg) at any point inside a uniform spherical shell is:
\(\displaystyle E_g = 0 \)
This means that if you were inside a hollow planet with a uniform mass distribution, you wouldn’t feel any gravitational pull from the shell itself, no matter where you are inside it. This is a surprising result that comes from the symmetry of the shell and is a beautiful example of how elegant physics can be. This concept is not only fascinating but also counterintuitive, as it tells us that inside a spherical shell, gravity doesn’t pull you in any direction at all.
Gravitational Field Resulting from a Uniform Solid Sphere
(i) Outside the Solid Sphere:
The field intensity is the same as if the entire mass of the sphere were concentrated at its center.
Consider a solid sphere with mass (M) and radius (R). The sphere is uniform, meaning its mass is evenly distributed throughout its volume. We want to calculate the gravitational field intensity (Eg) at a point that is at a distance (r) from the center of the sphere, where (r > R).
By applying the shell theorem, we can consider the mass of the sphere as if it were concentrated at its center for points outside the sphere. Based on Newton’s law of gravitation, the gravitational field intensity at a distance (r) from a point mass (M) is given by:
\(\displaystyle E_g = -\frac{G \cdot M}{r^2} \)
Since we are considering a point outside the sphere, the expression for (Eg) remains the same as for a point mass at the center of the sphere. Therefore, the gravitational field intensity (Eg) at a point outside a uniform solid sphere is:
\(\displaystyle E_g = -\frac{G \cdot M}{r^2} \)
This expression tells us that the gravitational field intensity outside a solid sphere decreases with the square of the distance from the center and is directed towards the center of the sphere. The derivation is straightforward because of the shell theorem, which allows us to treat the distributed mass of the sphere as if it were all located at the center of external points.
(ii) On the Surface of the Solid Sphere:
The intensity is given by the same formula as on the surface of the spherical shell.
We want to calculate the gravitational field intensity (Eg) at a point that lies on the surface of the sphere.
Based on Newton’s law of gravitation, the gravitational field intensity at a distance (r) from a point mass (M) is given by:
\(\displaystyle E_g = -\frac{G \cdot M}{r^2} \)
Since we are considering a point on the surface, the distance (r) is equal to the radius (R) of the sphere. Therefore, the gravitational field intensity (Eg) at a point on the surface of a uniform solid sphere is:
\(\displaystyle E_g = -\frac{G \cdot M}{R^2} \)
This expression tells us that the gravitational field intensity on the surface of a solid sphere is directed towards the center of the sphere and is a constant value for all points on the surface. The derivation is straightforward because the distance from any point on the surface to the center is simply the radius of the sphere.
(iii) Inside the Solid Sphere:
We’re interested in finding the gravitational field intensity (Eg) at a point inside this sphere, which means any point that is at a distance (r) from the center, where (r < R).
Gauss’s Law for Gravity states that the gravitational flux through a closed surface is proportional to the enclosed mass. For a point inside the sphere, only the mass enclosed within the radius (r) contributes to the gravitational field at that point.
If the sphere has a uniform density (ρ), the mass enclosed within radius (r) is given by the volume of that inner sphere times the density, which is (\(\displaystyle \frac{4}{3}\pi r^3 \rho \)).
The density (ρ) can be found by dividing the total mass (M) by the volume of the sphere, which is
( \(\displaystyle\frac{4}{3}\pi R^3 \)).
So,
( \(\displaystyle\rho = \frac{M}{\frac{4}{3}\pi R^3} \)).
Replace (ρ) in the expression for the enclosed mass to get
(\(\displaystyle m_{\text{enclosed}} = \frac{M}{\frac{4}{3}\pi R^3} \cdot \frac{4}{3}\pi r^3\) ).
The expression simplifies to
\(\displaystyle m_{\text{enclosed}} = \frac{M}{R^3} \cdot r^3 \) …(1)
Now, apply Newton’s law of gravitation for the enclosed mass to find (Eg):
\(\displaystyle E_g = -\frac{G \cdot m_{\text{enclosed}}}{r^2} \)
Replace (\(\displaystyle m_{\text{enclosed}} \)) with the expression from above eq (1):
\(\displaystyle E_g = -\frac{G \cdot \left(\frac{M}{R^3} \cdot r^3\right)}{r^2} \)
Simplify the expression to get the final result:
\(\displaystyle E_g = -\frac{G \cdot M \cdot r}{R^3} \)
The negative sign indicates that the gravitational field intensity is directed towards the center of the sphere. This expression shows that inside a uniform solid sphere, the gravitational field intensity increases linearly with distance from the center.
Gravitational Field due to a Uniform Disc at a Point on its Axis
Consider a disc with mass (M) and radius (R), where (O) is the center of the disc and (A) is a point on its axis located at a distance (r) from the center. The objective is to determine the gravitational field at point (A) the disc induces.
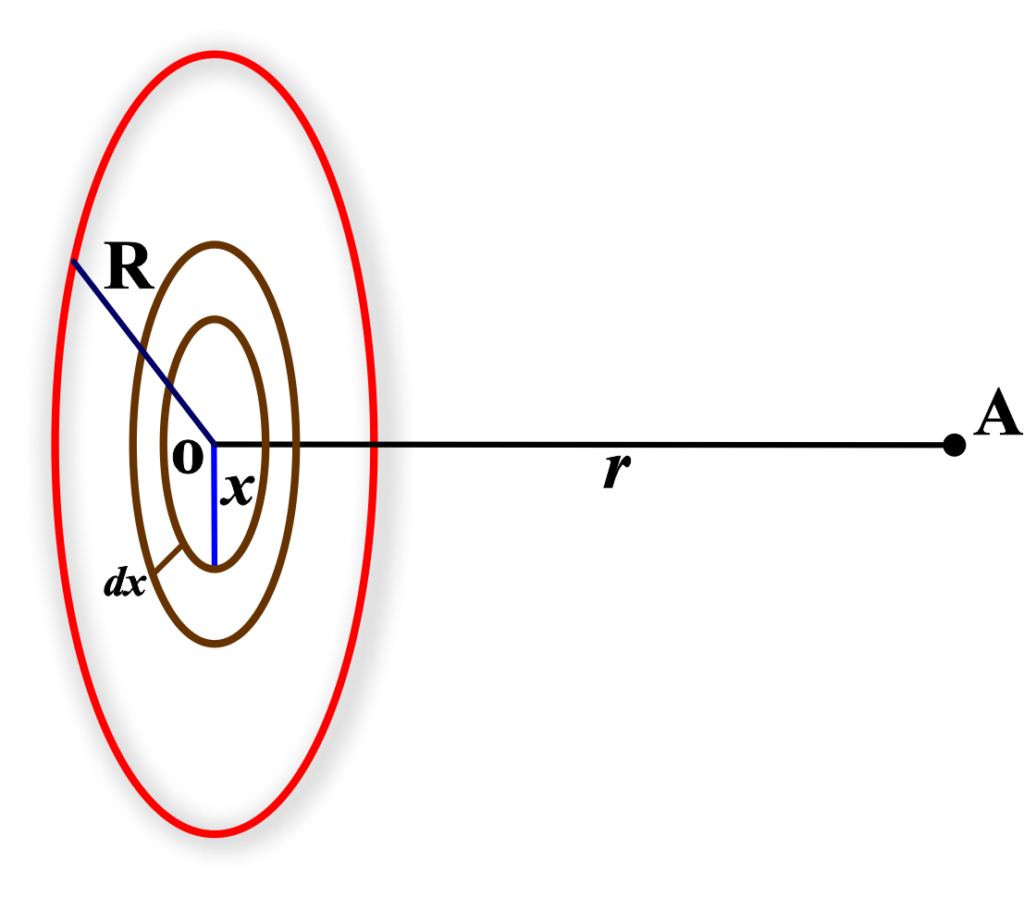
Consider a uniform disc disc with mass (M), radius (R), and uniform mass distribution. We want to find the gravitational field intensity (Eg) at a point (P) located at a distance (x) from the center of the disc along its axis.
Take a small ring element of thickness (dr) at a distance (r) from the center of the disc. The mass of this element, (dm), is given by the mass per unit area times the area of the ring:
\(\displaystyle dm = \sigma \cdot 2\pi r \cdot dr \)
where (σ ) is the mass per unit area of the disc.
The gravitational field intensity due to this ring element at point (P) is:
\(\displaystyle dE_g = \frac{G \cdot dm}{(r^2 + x^2)} \)
Here, (G) is the gravitational constant, and (\(\displaystyle (r^2 + x^2) \)) is the square of the distance from the element to point (P). The intensity (dEg) has a component along the axis of the disc, which is what we’re interested in. By symmetry, the components perpendicular to the axis cancel out.
The axial component of (dEg) is
\(\displaystyle dE_{g_{axial}} = dE_g \cdot \cos(\theta) \)
where (θ) is the angle between the line connecting the element to point (P) and the axis. Using the geometry,
\(\displaystyle\cos(\theta) = \frac{x}{\sqrt{r^2 + x^2}} \)
To find the total gravitational field intensity, integrate the axial component over the entire disc:
\(\displaystyle E_g = \int dE_{g_{axial}} = \int_0^R \frac{G \cdot dm \cdot x}{(r^2 + x^2)^{3/2}} \)
Replace (dm) with the expression from step 3 and integrate with respect to ( r ). After integrating, the expression for the gravitational field intensity due to the uniform disc at point (P) is:
\(\displaystyle E_g = \frac{2G \cdot M}{R^2} \left[ \frac{x}{\sqrt{R^2 + x^2}} – 1 \right] \)
The negative sign is omitted because we’re considering the magnitude of the field intensity, and by convention, we take the direction toward the disc as positive. This derivation shows that the gravitational field intensity due to a disc is not uniform and depends on the distance from the disc’s center along its axis.
Also Read: Gravitational Potential
Solved Examples
Problem 1: Calculate the gravitational field intensity at a point 10 meters away from a point mass of 5 kg.
Solution: The gravitational field intensity ( \(\displaystyle\vec{E} \)) due to a point mass (M) at a distance (r) is given by:
\(\displaystyle \vec{E} = -\frac{GM}{r^2} \hat{r} \)
Calculate (E):
\(\displaystyle E = -\frac{6.674 \times 10^{-11} \times 5}{10^2}\)
\(\displaystyle E = -\frac{3.337 \times 10^{-10}}{100} \)
\(\displaystyle E = -3.337 \times 10^{-12} \, \text{N/kg}\)
Therefore, the gravitational field intensity at 10 meters away from a 5 kg point mass is (\(\displaystyle -3.337 \times 10^{-12} \, \text{N/kg} \)).
Problem 2: Calculate the gravitational field intensity at a point on the axis of a ring of mass (2 kg) and radius (1 m) at a distance (1 m) from the center of the ring.
Solution: The gravitational field intensity (E) at a point on the axis of a ring of mass (M), radius (R), and distance (x) from the center of the ring is given by:
\(\displaystyle E = -\frac{GMx}{(R^2 + x^2)^{3/2}} \)
Calculate (E):
\(\displaystyle E = -\frac{6.674 \times 10^{-11} \times 2 \times 1}{(1^2 + 1^2)^{3/2}} \)
\(\displaystyle E = -\frac{1.3348 \times 10^{-10}}{(2)^{3/2}} \)
\(\displaystyle E = -\frac{1.3348 \times 10^{-10}}{2.828} \)
\(\displaystyle E = -4.721 \times 10^{-11} \, \text{N/kg} \)
Therefore, the gravitational field intensity at a point on the axis of the ring is (\(\displaystyle -4.721 \times 10^{-11} \, \text{N/kg} \)).
Problem 3: Calculate the gravitational field intensity at a point 3 meters away from the center of a uniform spherical shell of mass (10 kg) and radius (2 m).
Solution: For a point outside a uniform spherical shell, the gravitational field intensity (E) is the same as if all the mass (M) were concentrated at the center:
\(\displaystyle E = -\frac{GM}{r^2} \)
Calculate (E):
\(\displaystyle E = -\frac{6.674 \times 10^{-11} \times 10}{3^2} \)
\(\displaystyle E = -\frac{6.674 \times 10^{-10}}{9} \)
\(\displaystyle E = -7.416 \times 10^{-11} \, \text{N/kg} \)
Therefore, the gravitational field intensity at a point 3 meters away from the center of the spherical shell is (\(\displaystyle -7.416 \times 10^{-11} \, \text{N/kg} \)).
Problem 4: Calculate the gravitational field intensity at a point 4 meters away from the center of a uniform solid sphere of mass (15 kg) and radius (2 m).
Solution: For a point outside a uniform solid sphere, the gravitational field intensity ( E ) is the same as if all the mass ( M ) were concentrated at the center:
\(\displaystyle E = -\frac{GM}{r^2} \)
Calculate (E):
\(\displaystyle E = -\frac{6.674 \times 10^{-11} \times 15}{4^2} \)
\(\displaystyle E = -\frac{1.0011 \times 10^{-9}}{16} \)
\(\displaystyle E = -6.257 \times 10^{-11} \, \text{N/kg} \)
Therefore, the gravitational field intensity at a point 4 meters away from the center of the solid sphere is (\(\displaystyle -6.257 \times 10^{-11} \, \text{N/kg} \)).
Problem 5: Calculate the gravitational field intensity at a point 1 meter away from the center of a uniform solid sphere of mass ( 20 kg) and radius (3 m).
Solution: For a point inside a uniform solid sphere, the gravitational field intensity ( E ) is given by:
\(\displaystyle E = -\frac{GMr}{R^3} \)
Calculate ( E ):
\(\displaystyle E = -\frac{6.674 \times 10^{-11} \times 20 \times 1}{3^3} \)
\(\displaystyle E = -\frac{1.3348 \times 10^{-9}}{27} \)
\(\displaystyle E = -4.944 \times 10^{-11} \, \text{N/kg} \)
Therefore, the gravitational field intensity at a point 1 meter away from the center of the solid sphere is (\(\displaystyle -4.944 \times 10^{-11} \, \text{N/kg} \)).
FAQs
What is a gravitational field?
A gravitational field is a region of space surrounding a mass where another mass experiences a force of gravitational attraction. It represents the influence that a mass exerts on other masses in its vicinity, causing them to accelerate towards it.
How is gravitational field intensity defined?
Gravitational field intensity, or gravitational field strength, is defined as the gravitational force experienced by a unit mass placed at a point in the field. It indicates the strength and direction of the gravitational field at that point.
What factors affect the gravitational field intensity at a point?
Gravitational field intensity at a point is affected by the mass of the object creating the field and the distance from the object to the point in question. The intensity decreases with the square of the distance from the mass and increases with the mass itself.
How does the gravitational field intensity vary with distance from a mass?
Gravitational field intensity decreases with the square of the distance from the mass. This means that if the distance from the mass is doubled, the gravitational field intensity becomes one-fourth of its original value.
What is the significance of a gravitational field in celestial mechanics?
In celestial mechanics, the gravitational field is crucial for understanding the motions of planets, moons, and other celestial bodies. It determines the orbits of planets around stars, moons around planets, and the trajectories of comets and asteroids.
Can the gravitational field intensity be zero? If so, under what conditions?
Yes, gravitational field intensity can be zero at points called null points or equilibrium points. This can occur at a point between two masses where the gravitational forces due to each mass cancel each other out, resulting in zero net gravitational field intensity.
How is gravitational field intensity related to gravitational potential energy?
Gravitational field intensity is related to the gradient of gravitational potential energy. It points in the direction of the steepest decrease of potential energy and is equal to the negative gradient of the gravitational potential. This relationship helps in understanding the motion of objects within a gravitational field.
