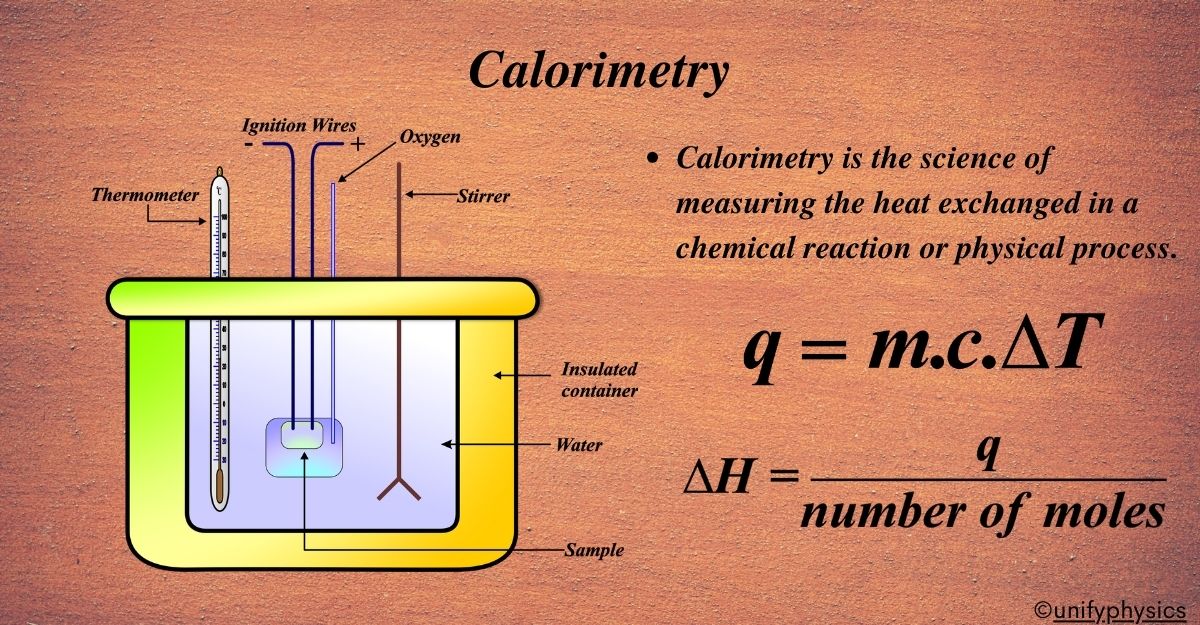
Calorimetry

Calorimetry is like the science of measuring the heat version of a story. It tells us how much energy is involved in chemical reactions or physical changes, and it has a story that goes back centuries.

The concept of measuring heat goes back to the ancient Greeks, who were curious about heat and temperature. However, the real story of calorimetry begins in the late 18th century.

Around 1780, the famous French chemist Antoine Lavoisier and the mathematician Pierre-Simon Laplace worked together to develop the ice calorimeter. This device measured the heat released or absorbed by a chemical reaction through the melting of ice.

In the mid-19th century, James Prescott Joule conducted experiments that showed heat is a form of energy. He used calorimetry to demonstrate the mechanical equivalent of heat, laying the groundwork for the law of conservation of energy.

Today, calorimetry has evolved with sophisticated instruments like bomb calorimeters and differential scanning calorimeters. These tools allow scientists to measure heat with great precision and apply this knowledge in fields like chemistry, biology, and materials science.

What Is a Calorimeter?

A calorimeter is a device that measures the amount of heat absorbed or released during a chemical reaction, physical change, or some processes. It’s essentially a thermal container that can be as simple as a coffee cup or as sophisticated as a bomb calorimeter, depending on the experiment’s requirements.

Imagine you have two substances that react together and produce heat. If you place them in a calorimeter, it will capture all the heat from the reaction. By measuring the temperature change of the water or another fluid surrounding the reaction chamber, you can figure out exactly how much heat was produced or consumed.

Typically, a calorimeter consists of a reaction vessel where the chemical reaction or physical change takes place. This vessel is surrounded by an insulating layer to prevent heat loss to the environment, ensuring that all the heat exchange is measured accurately. A thermometer is inserted through the top of the calorimeter to monitor the temperature change. This change tells us how much heat energy was involved in the process happening inside.

Process Inside a Calorimeter

Inside the calorimeter, when substances react or change state, their molecules absorb or release energy in the form of heat. This is like the molecules doing a dance where they either get excited and move around more (absorb energy) or slow down and relax (release energy).

The calorimeter is designed to measure this ‘dance’ by tracking the temperature change. If the reaction releases heat (exothermic), the temperature inside the calorimeter goes up. If the reaction absorbs heat (endothermic), the temperature goes down.

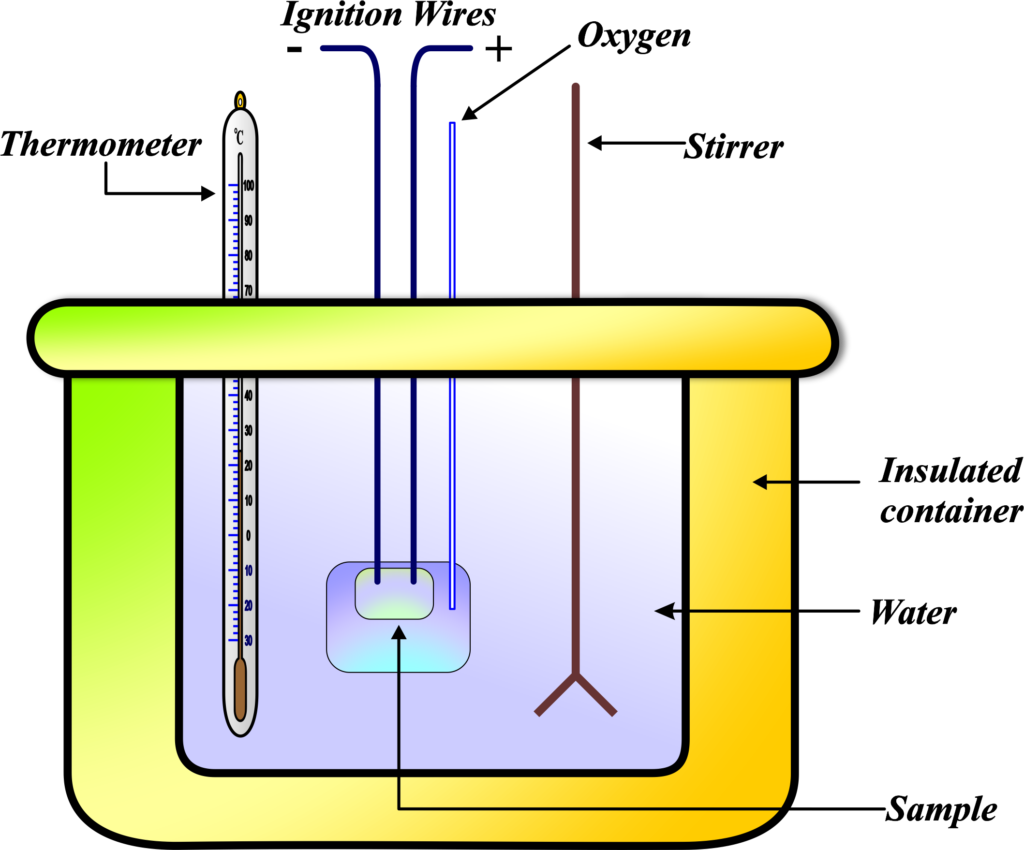
Often, the substance inside the calorimeter is surrounded by water because water is great at absorbing or releasing heat. The temperature change of this water tells us exactly how much heat was involved in the process inside. The calorimeter is insulated to prevent heat from escaping to the surroundings. This way, all the heat transfer is contained within the calorimeter, ensuring accurate measurements.

By measuring the initial and final temperatures and knowing the specific heat capacity of the substances involved, we can calculate the heat change. This gives us a clear picture of the energy involved in the reaction or physical change happening inside the calorimeter. A calorimeter is like a thermal camera that captures the ‘heat picture’ of a process, allowing us to quantify the energy changes without seeing the actual molecular action.

Also Read: Heat Capacity

Calorimeter Principle

The principle behind a calorimeter is based on the law of conservation of energy, which states that energy cannot be created or destroyed, only transformed. In calorimetry, the heat lost by a hot object is equal to the heat gained by a cooler one until thermal equilibrium is reached. This principle allows us to measure the heat transfer associated with chemical reactions or physical changes.

Imagine you have a hot cup of coffee and cold milk. If you pour the cold milk into the hot coffee, the milk will warm up, and the coffee will cool down. They exchange heat until they reach the same temperature. This is similar to what happens in a calorimeter.

A calorimeter works on the principle that when two substances at different temperatures come into contact with it, heat will flow from the hotter substance to the cooler one until they reach the same temperature. This is known as reaching thermal equilibrium. The principle of calorimetry is based on the law of conservation of energy, which states that energy cannot be created or destroyed, only transferred. In the context of calorimetry, this means the heat lost by the hot substance is exactly equal to the heat gained by the cold substance.

The heat transfer is calculated using the formula:

\(\displaystyle q = mc\Delta T \)

• (q) is the heat transferred,
• (m) is the mass of the substance,
• (c) is the specific heat capacity of the substance,
• (∆T ) is the change in temperature.

Types of Calorimeter

There are several types of calorimeters, each designed for specific types of measurements:

1) Adiabatic Calorimeters

• Think of an adiabatic calorimeter as a super-insulated flask that doesn’t allow any heat to escape or enter. When a reaction happens inside this calorimeter, all the heat has to stay within the system, causing the temperature to change. This type of calorimeter is used to study reactions that might release a lot of heat quickly, like combustion.

2) Reaction Calorimeters

• A reaction calorimeter is like a mini-lab where chemical reactions take place in a controlled environment. It measures the heat of the reaction while maintaining a constant temperature. It’s like cooking on a stove with a very sensitive thermometer—you can track how much heat your cooking reaction is giving off or absorbing.

3) Bomb Calorimeters

• Imagine a strong, sealed container that can withstand high pressure—this is a bomb calorimeter. It’s used to measure the heat of combustion of a substance. You can think of it as measuring how much “firepower” a substance has by burning it in an oxygen-rich chamber and measuring the heat produced.
• By supplying excess oxygen, bomb calorimetry prevents any incomplete combustion, which could result in inaccurate heat measurements. Incomplete combustion may lead to the formation of carbon monoxide or other incomplete combustion products, which could interfere with the calorimetric analysis.
• Oxygen in calorimetry, particularly in bomb calorimetry, facilitates complete combustion of the sample, ensures efficient heat transfer to the calorimeter, and helps eliminate interference from incomplete combustion products, thereby enabling accurate measurement of the heat of combustion.

4) Constant Pressure Calorimeters

• These are the everyday calorimeters you might use in a school lab. They operate at the same pressure as the surrounding air. If you’ve ever mixed vinegar and baking soda in a flask and measured the temperature change, you’ve used a constant pressure calorimeter.

5) Differential Scanning Calorimeters

• Differential scanning calorimeters are like thermal race tracks, comparing how a sample and a reference material respond to heat. They tell us how much more or less heat a substance absorbs or releases compared to a known standard as they’re heated or cooled.

Uses of Calorimetry

Calorimetry has a wide range of applications, including:

• Calorimetry helps us find out how much heat is produced or absorbed during a chemical reaction. It’s like measuring how much energy is released when you pop a bag of popcorn in the microwave.
• Food scientists use calorimetry to determine the calorie content of foods. It’s similar to figuring out how much fuel (calories) you’re getting from different snacks to keep you going throughout the day.
• Calorimetry can measure the heat involved when a substance changes from solid to liquid (melting) or liquid to gas (evaporation). It’s like tracking how much ice you need to cool a drink or how long it takes for water to boil away.
• This technique helps us calculate the heat capacity of different materials, which tells us how much heat a substance can store. It’s like understanding why a metal spoon gets hot quickly in soup, while a wooden spoon does not.
• Calorimetry is used to study enthalpy changes in substances, which is the heat content at constant pressure. It’s important to understand how much energy is involved in making or breaking chemical bonds.
• Scientists use calorimetry to measure the heat produced by organisms, which helps in understanding energy flow in ecosystems. It’s like figuring out how much heat a group of animals generates and how it affects their environment.

Calculating Enthalpy Change using Calorimetry

Imagine you’re experimenting with mixing two chemicals in a calorimeter and measuring the temperature change. This change tells us how much heat was involved in the reaction. To find the enthalpy change (∆ H), which is the heat change at constant pressure, we use the following steps:

Record the temperature of the reactants before and after the reaction. The difference between these two temperatures (∆T) is crucial for our calculation. Use the formula:

\(\displaystyle\begin{equation}\label{eqn:1}\boxed{\boldsymbol{q = m \cdot c \cdot \Delta T }} \end{equation}\)

• (q) is the heat exchanged,
• (m) is the mass of the substance (usually the solvent like water),
• (c) is the specific heat capacity (for water, it’s approximate \(\displaystyle 4.18 \, \text{J/g}^\circ\text{C} )\),
• (∆T) is the temperature change.

To get the enthalpy change per mole, divide the heat exchanged by the number of moles of the reactant:

\(\displaystyle\begin{equation}\label{eqn:2}\boxed{\boldsymbol{ \Delta H = \frac{q}{\text{number of moles}}}} \end{equation}\)

If the reaction is exothermic (releases heat), (∆H) will be negative. If it’s endothermic (absorbs heat), (∆H ) will be positive.

Example: You mix a chemical with water, and the temperature rises from 20°C to 25°C. you have 100 grams of water, and the reaction involved 0.5 moles of the chemical. Here’s how you’d calculate (∆H):

\(\displaystyle \Delta T = 25^\circ\text{C} – 20^\circ\text{C} = 5^\circ\text{C} \)

\(\displaystyle q = 100 \, \text{g} × 4.18 \, \text{J/g}^\circ\text{C} × 5^\circ\text{C} = 2090 \, \text{J} \)

\(\displaystyle \Delta H = \frac{2090 \, \text{J}}{0.5 \, \text{moles}} = 4180 \, \text{J/mole} \)

Since the temperature increased, the reaction is exothermic, so (∆H) would be \(\displaystyle -4180 \, \text{J/mole} \).

Solved Examples

Problem 1: A 100 g sample of water at 80°C is mixed with 200 g of water at 30°C in an insulated container. What is the final temperature of the mixture?

Solution:

• Mass of hot water (m₁) = 100 g
• Initial temperature of hot water (T₁) = 80°C
• Mass of cold water (m₂) = 200 g
• Initial temperature of cold water (T₂) = 30°C
• Specific heat capacity of water (c) = 4.18 J/g°C

Let the final temperature of the mixture be (T_f).

Using the principle of conservation of energy, the heat lost by hot water is equal to the heat gained by cold water:

\(\displaystyle m_1 c (T_1 – T_f) = m_2 c (T_f – T_2) \)

\(\displaystyle 100 \times 4.18 \times (80 – T_f) = 200 \times 4.18 \times (T_f – 30) \)

Solving for (T_f):

\(\displaystyle 100 \times (80 – T_f) = 200 \times (T_f – 30) \)

\(\displaystyle 8000 – 100T_f = 200T_f – 6000 \)

\(\displaystyle 8000 + 6000 = 300T_f \)

\(\displaystyle 14000 = 300T_f \)

\(\displaystyle T_f = \frac{14000}{300} \)

T_f = 46.67°C

The final temperature of the mixture is 46.67°C.

Problem 2: A 50 g piece of metal at 200°C is placed in 100 g of water at 20°C. If the final temperature of the system is 25°C, what is the specific heat capacity of the metal? Assume no heat is lost to the surroundings.

Solution:

• Mass of metal (m₁) = 50 g
• Initial temperature of metal (T₁) = 200°C
• Mass of water (m₂) = 100 g
• Initial temperature of water (T₂) = 20°C
• Final temperature (T_f) = 25°C
• Specific heat capacity of water (c₂) = 4.18 J/g°C
• Specific heat capacity of metal (c₁) = ?

Using the principle of conservation of energy, the heat lost by metal is equal to the heat gained by water:

\(\displaystyle m_1 c_1 (T_1 – T_f) = m_2 c_2 (T_f – T_2) \)

\(\displaystyle 50 \times c_1 \times (200 – 25) = 100 \times 4.18 \times (25 – 20) \)

\(\displaystyle 50 \times c_1 \times 175 = 100 \times 4.18 \times 5 \)

\(\displaystyle 50 \times c_1 \times 175 = 2090 \)

\(\displaystyle 8750c_1 = 2090 \)

\(\displaystyle c_1 = \frac{2090}{8750} \)

\(\displaystyle c_1 = 0.239 J/g°C \)

The specific heat capacity of the metal is 0.239 J/g°C.

Problem 3: A 150 g piece of ice at 0°C is added to 500 g of water at 40°C. Calculate the final temperature of the mixture. (Latent heat of fusion of ice = 334 J/g)

Solution:

• Mass of ice (m₁) = 150 g
• Initial temperature of ice (T₁) = 0°C
• Mass of water (m₂) = 500 g
• Initial temperature of water (T₂) = 40°C
• Specific heat capacity of water (c) = 4.18 J/g°C
• Latent heat of fusion of ice (L_f) = 334 J/g

First, calculate the heat required to melt the ice:

\(\displaystyle Q_1 = m_1 L_f \)

\(\displaystyle Q_1 = 150 \times 334 \)

Q₁ = 50100 J

Next, calculate the heat available from the cooling water:

\(\displaystyle Q_2 = m_2 c (T_2 – 0) \)

\(\displaystyle Q_2 = 500 \times 4.18 \times 40 \)

Q₂ = 83600 J

Since (Q₂) is greater than (Q₁), all the ice will melt. The remaining heat will be used to raise the temperature of the water:

\(\displaystyle Q_{remaining} = Q_2 – Q_1 \)

\(\displaystyle Q_{remaining} = 83600 – 50100 \)

\(\displaystyle Q_{remaining} = 33500 \, J \)

Now, use the remaining heat to find the final temperature:

\(\displaystyle Q_{remaining} = (m_1 + m_2) c \Delta T \)

\(\displaystyle 33500 = (150 + 500) \times 4.18 \times \Delta T \)

\(\displaystyle 33500 = 650 \times 4.18 \times \Delta T \)

\(\displaystyle 33500 = 2717 \Delta T\)

\(\displaystyle\Delta T = \frac{33500}{2717}\)

\(\displaystyle \Delta T = 12.33°C \)

Since the final temperature will be above 0°C, add this change to 0°C:

\(\displaystyle T_f = 0 + 12.33 \)

The final temperature of the mixture is 12.33°C.

Problem 4: A 300 g piece of aluminum at 100°C is mixed with 200 g of copper at 50°C in an insulated container. Find the final temperature of the mixture. The specific heat capacities are 0.897 J/g°C for aluminum and 0.385 J/g°C for copper.

Solution:

• Mass of aluminum (m_Al) = 300 g
• Initial temperature of aluminum (T_Al) = 100°C
• Mass of copper (m_Cu) = 200 g
• Initial temperature of copper (T_Cu) = 50°C
• Specific heat capacity of aluminum (c_Al) = 0.897 J/g°C
• Specific heat capacity of copper (c_Cu) = 0.385 J/g°C

Let the final temperature of the mixture be (T_f).

Using the principle of conservation of energy:

\(\displaystyle m_{Al} c_{Al} (T_{Al} – T_f) = m_{Cu} c_{Cu} (T_f – T_{Cu}) \)

\(\displaystyle 300 \times 0.897 \times (100 – T_f) = 200 \times 0.385 \times (T_f – 50) \)

\(\displaystyle 269.1 \times (100 – T_f) = 77 \times (T_f – 50) \)

\(\displaystyle 26910 – 269.1 T_f = 77 T_f – 3850 \)

\(\displaystyle 26910 + 3850 = 269.1 T_f + 77 T_f \)

\(\displaystyle 30760 = 346.1 T_f \)

\(\displaystyle T_f = \frac{30760}{346.1} \)

\(\displaystyle T_f \approx 88.87°C \)

The final temperature of the mixture is approximately 88.87°C.

Problem 5: A 200 g piece of ice at -10°C is placed in 300 g of water at 50°C. Calculate the final temperature of the mixture. (Specific heat capacity of ice = 2.1 J/g°C, specific heat capacity of water = 4.18 J/g°C, latent heat of fusion of ice = 334 J/g)

Solution:

• Mass of ice (m_ice) = 200 g
• Initial temperature of ice (T_ice) = -10°C
• Mass of water (m_water) = 300 g
• Initial temperature of water (T_water) = 50°C
• Specific heat capacity of ice (c_ice) = 2.1 J/g°C
• Specific heat capacity of water (c_water) = 4.18 J/g°C
• Latent heat of fusion of ice (L_f) = 334 J/g

First, calculate the heat required to warm the ice from -10°C to 0°C:

\(\displaystyle Q_1 = m_{ice} c_{ice} \Delta T \)

\(\displaystyle Q_1 = 200 \times 2.1 \times 10 \)

\(\displaystyle Q_1 = 4200 \, J \)

Next, calculate the heat required to melt the ice:

\(\displaystyle Q_2 = m_{ice} L_f \)

\(\displaystyle Q_2 = 200 \times 334 \)

\(\displaystyle Q_2 = 66800 \, J \)

Total heat required to bring ice to water at 0°C:

\(\displaystyle Q_{total} = Q_1 + Q_2 \)

\(\displaystyle Q_{total} = 4200 + 66800 \)

\(\displaystyle Q_{total} = 71000 \, J \)

Now, calculate the heat available from cooling the water:

\(\displaystyle Q_{water} = m_{water} c_{water} \Delta T \)

\(\displaystyle Q_{water} = 300 \times 4.18 \times (50 – 0) \)

\(\displaystyle Q_{water} = 62700 \, J \)

Since (\(\displaystyle Q_{water} < Q_{total} \)), not all ice will melt, and the final temperature will be 0°C. The final temperature of the mixture is 0°C, and not all ice will melt.

Problem 6: A 150 g piece of lead at 100°C is placed in 250 g of water at 20°C in a calorimeter. The specific heat capacities are 0.128 J/g°C for lead and 4.18 J/g°C for water. If the final temperature of the mixture is 21°C, calculate the heat lost by lead and the heat gained by water.

Solution:

• Mass of lead (m_Pb) = 150 g
• Initial temperature of lead (T_Pb) = 100°C
• Mass of water (m_water) = 250 g
• Initial temperature of water (T_water) = 20°C
• Final temperature (T_f) = 21°C
• Specific heat capacity of lead (c_Pb) = 0.128 J/g°C
• Specific heat capacity of water (c_water) = 4.18 J/g°C

Heat lost by lead:

\(\displaystyle Q_{Pb} = m_{Pb} c_{Pb} (T_{Pb} – T_f) \)

\(\displaystyle Q_{Pb} = 150 \times 0.128 \times (100 – 21) \)

\(\displaystyle Q_{Pb} = 150 \times 0.128 \times 79 \)

\(\displaystyle Q_{Pb} = 1516.8 \, J \)

Heat gained by water:

\(\displaystyle Q_{water} = m_{water} c_{water} (T_f – T_{water}) \)

\(\displaystyle Q_{water} = 250 \times 4.18 \times (21 – 20) \)

\(\displaystyle Q_{water} = 250 \times 4.18 \times 1\)

\(\displaystyle Q_{water} = 1045 \, J \)

The heat lost by lead is 1516.8 J, and the heat gained by water is 1045 J.

FAQs