The story of the capacitor begins in the 18th century. It was a time of great scientific discovery, and among the many inventions of the era, the capacitor holds a special place.
The earliest forms of capacitors were known as Leyden jars. These were simple devices consisting of water-filled glass jars. In the 1740s, European experimenters like Ewald Georg von Kleist and Pieter van Musschenbroek independently discovered that electric charge could be stored in these jars.
A Leyden jar is made by placing a metal rod into the jar, which is partially filled with water. The rod collects electric charge, which is then stored in the water. The glass of the jar acts as the dielectric—a material that doesn’t conduct electricity but can support an electric field.
Over time, capacitors have evolved from these simple jars to the complex and varied components we use today. They’ve become essential in electronic circuits, used for tasks like blocking direct current while allowing alternating current to pass, smoothing the output of power supplies, tuning radios to specific frequencies, and stabilizing voltage and power flow.
Today, capacitors come in all shapes and sizes, with a range of materials used as dielectrics, including ceramic, plastic film, paper, mica, and even air. The basic principle, however, remains the same: capacitors store and release electrical energy.
What Is a Capacitor?
A capacitor is a fundamental electronic component that stores electrical energy in an electric field. It consists of two conductive plates separated by an insulating material called a dielectric. The plates can be made of various materials, such as metal, and the dielectric can be air, paper, plastic, or ceramic.
Imagine you have a little box that can hold and store some amount of invisible energy. Now, in the world of electronics, this ‘little box’ is what we call a capacitor. It’s not a box in the literal sense, but it serves a similar purpose: it stores electrical energy, just like a box stores physical items.
A capacitor is made up of two metal plates that are very close to each other but do not touch. Between these plates, there’s a non-conductive material called a dielectric. This dielectric can be made of various materials like glass, ceramic, plastic film, or even air.
When you connect a battery or a power source to a capacitor, one plate becomes positively charged, and the other becomes negatively charged. The positive charge doesn’t jump over to the negative side because the dielectric stops it. This separation of charges creates an electric field and stores energy.
You can think of the electric field as a sort of invisible force field between the plates. It’s this field that holds onto the energy until the capacitor is connected to something that can use that energy, like a light bulb or a motor.
When the capacitor is connected to a circuit, it releases the stored energy to power electronic devices. It can release this energy much faster than a battery, which is why capacitors are used when a quick burst of energy is needed.
To help you visualize, imagine a water tank with a pipe at the bottom. When you fill the tank with water, the water doesn’t immediately flow out because of a valve (like the dielectric in a capacitor). When you open the valve (connect the capacitor to a circuit), the water (energy) rushes out quickly.
How Does a Capacitor Work?
When a voltage is applied across the terminals, an electric field is created in the capacitor, which stores energy. Think of a capacitor as a tiny energy warehouse. It doesn’t create energy; it stores it for later use. Here’s how it works:
When you connect a capacitor to a power source, like a battery, something interesting happens. One plate of the capacitor starts collecting negative charges, and electrons, from the battery. The other plate gives up its electrons to the battery, becoming positively charged. This process is called charging the capacitor.
Between the two plates of the capacitor, there’s a non-conductive material called a dielectric. This could be air, ceramic, plastic, or any other materials. The dielectric’s job is to keep the charges on each plate from reaching each other and canceling out.
As the plates charge up, an electric field forms between them. This field is where the energy is stored. The strength of this field, and therefore the amount of energy the capacitor can store, depends on a few things: the size of the plates, the distance between them, and the type of dielectric.
When the power source is removed, the capacitor doesn’t just lose all its charge immediately. Instead, it holds onto the energy. If you then connect the capacitor to something that uses electricity, like a motor, the capacitor releases its stored energy to power the device. This release is called discharging.
It’s important to note that while it seems like electricity is flowing through the capacitor, it’s not really. The dielectric stops that. What’s happening is the capacitor is releasing the charge it stored earlier, which then flows through the circuit.
Capacitors can release their energy much faster than batteries, which is why they’re used when a device needs a quick burst of power. A good example of a capacitor at work is in a camera flash. The capacitor charges up slowly from the battery, and then when you take a picture, it releases all that energy in an instant to create a flash of light.
Capacitance
Capacitance is essentially a measure of how good a capacitor is at holding charge. A capacitor with a high capacitance can hold more charge at a lower voltage, while a capacitor with a low capacitance can’t hold as much charge before the voltage gets too high.
Imagine you’re at a party and you have a balloon. You start filling it with air. The more air you put in, the bigger it gets, right? Now, let’s swap the air for an electric charge and the balloon for a capacitor. Capacitance is like the ‘stretchiness’ of the balloon—it tells you how much electric charge you can stuff into your capacitor before it’s full.
The basic formula for capacitance is pretty straightforward:
\(\displaystyle C = \frac{Q}{V} \)
- (C) is the capacitance,
- (Q) is the total charge stored, and
- (V) is the voltage across the capacitor.
The unit of capacitance is the farad (F), named after Michael Faraday. One farad is pretty huge, so you’ll often see capacitors rated in microfarads (µF), nanofarads (nF), or picofarads (pF).
A few things affect how much charge a capacitor can hold:
- The size of the plates: Bigger plates can hold more charge.
- The distance between the plates: Closer plates can hold more charge.
- The type of dielectric: Different materials let you store different amounts of charge.
Think of capacitance like a bucket for rainwater. The size of the bucket is like the size of the plates (more area, more water). The height of the bucket is like the voltage (higher voltage, taller bucket). And the quality of the bucket material is like the dielectric (better material, less leakage).
Capacitance is crucial because it determines how much energy you can store and release in circuits. It’s like having a reservoir of energy that you can tap into whenever you need a quick burst of power.
How does capacitance affect the time it takes to charge or discharge a capacitor?
The capacitance of a capacitor plays a significant role in determining how quickly it can charge or discharge. Capacitance, measured in farads, indicates how much charge a capacitor can store. A higher capacitance means the capacitor can store more charge.
The time it takes for a capacitor to charge or discharge is often described by the time constant (τ), which is the product of the resistance (R) in the circuit and the capacitance (C) of the capacitor:
\(\displaystyle \tau = RC \)
This time constant tells us how long it will take for the capacitor to charge up to about 63% of the supply voltage or discharge to about 37% of its initial charge. A larger capacitance will result in a larger time constant if the resistance is constant. This means the capacitor will take longer to charge up to its full capacity because it can hold more charge.
Similarly, when discharging, a capacitor with a larger capacitance will take longer to release all its stored charge compared to one with a smaller capacitance.
In practical terms, if you have a circuit that needs to respond quickly, you might want a capacitor with a smaller capacitance so it can charge and discharge rapidly. Conversely, if you need to maintain power for a longer duration, a larger capacitance would be beneficial as it would discharge more slowly.
The larger the capacitance, the more charge the capacitor can hold, and thus, the longer it takes to change its state of charge. This affects both the charging and discharging processes, influencing how capacitors are used in various electronic applications.
Standard Units of Capacitance:
When we talk about the standard unit of capacitance, we’re referring to the farad (F). It’s named after the famous scientist Michael Faraday. But what does this unit represent? A farad is quite a large unit. It’s defined as the amount of capacitance that can store one coulomb (C) of electric charge per one volt (V) of potential difference across the capacitor.
In mathematical terms, it’s expressed as:
\(\displaystyle 1 \text{F} = 1 \text{C}/1 \text{V} \)
Smaller Units:
| Prefix Name | Abbreviation | Weight (Power of Ten) | Equivalent Farads |
|---|---|---|---|
| Kilo farad | kF | 103 | 1000 F |
| Millifarad | mF | 10-3 | 0.001 F |
| Microfarad | µF | 10-6 | 0.000001 F |
| Nanofarad | nF | 10-9 | 0.000000001 F |
| Picofarad | pF | 10-12 | 0.000000000001 F |
This table helps students understand how capacitance is measured and how these units relate to the standard farad. It’s important to note that in practical applications, capacitors are often labeled with these smaller units due to the large size of a single farad.
To put it into perspective, imagine a small capacitor used in a radio. It might have a capacitance of just a few nanofarads. On the other hand, a capacitor used for a camera flash might be rated in microfarads because it needs to store more energy.
The unit of capacitance is crucial because it helps us understand how much charge a capacitor can hold and how it will behave in a circuit. It’s like knowing the size of a water tank; it tells you how much water you can store.
Factors Affecting Capacitance
When we talk about capacitance, we’re referring to a capacitor’s ability to store charge. Just like certain factors can affect how much water a sponge can hold, there are specific factors that determine how much charge a capacitor can store.
Size of the Plates: More surface area means more space for charge to accumulate, increasing capacitance and less surface area means less space for charge, decreasing capacitance.
Distance Between the Plates: When the plates are closer together, the electric field between them is stronger, which increases capacitance. If the plates are further apart, the electric field is weaker, and the capacitance decreases. The size of the Plates is like the width and length of the tank—the bigger it is, the more water it can hold.
Dielectric Material: The material placed between the plates, known as the dielectric, affects how well the electric field can form. Some materials create stronger fields than others. This is a measure of how well a material can support an electric field. Materials with higher permittivity increase the capacitance because they allow more charge to be stored for the same voltage. Distance Between the Plates is like the height of the tank walls—shorter walls make it easier to fill the tank to the brim.
Shape of the Plates: The shape of the plates can also influence capacitance. Different shapes can affect the distribution of charge and the electric field, thus affecting the capacitance. Dielectric Material is like the material of the tank—some materials might hold water better without leaking.
Energy Stored in a Capacitor
A capacitor storing energy is like a stretched rubber band holding potential energy. When you stretch a rubber band, you do work, and it holds that energy until you let go. Similarly, when you charge a capacitor, you work against the electric field between the plates, and this work is stored as electrical potential energy.
The energy (U) stored in a capacitor can be calculated using the formula:
\(\displaystyle U = \frac{1}{2}CV^2 \)
Understanding the Formula:
- (C): The capacitance tells us how much charge the capacitor can hold. More capacitance means more energy storage capacity.
- (V2): The voltage squared shows that the energy increases rapidly with the voltage. It’s like lifting that bucket of water higher and higher—the potential energy increases with height.
Example: Consider a camera flash. The capacitor in the flash circuit stores energy when you charge it by pressing the button. When you take a picture, the capacitor releases all its stored energy in a quick burst to produce a flash of light.
Imagine a water tower with a tank at the top. The amount of water it can hold represents the capacitance, and the height of the tower represents the voltage. The potential energy of the water (due to gravity) is analogous to the energy stored in the capacitor (due to the electric field).
The energy stored in capacitors is crucial for devices that need a quick release of power. It’s used in defibrillators to deliver a life-saving shock, in computers to maintain power supply stability, and in audio systems to manage power demands.
Derivation of Energy Stored in a Capacitor:
When a capacitor is connected to a battery, the battery does work to move charge from one plate of the capacitor to the other. This work is stored as electrical potential energy in the capacitor.
Assume the capacitor starts with no charge and reaches a charge (Q) when fully charged. To move a small amount of charge (dQ) from one plate to another against a potential difference (V), the work done (dW) is:
\(\displaystyle dW = V \cdot dQ \)
The voltage (V) across the capacitor at any instant is related to the charge (Q) on it by the capacitance (C):
\(\displaystyle V = \frac{Q}{C} \)
Replace (V) in the work done equation with (Q/C):
\(\displaystyle dW = \frac{Q}{C} \cdot dQ \)
To find the total work done (W) to charge the capacitor from (0) to (Q), integrate (dW):
\(\displaystyle W = \int_{0}^{Q} \frac{Q}{C} \cdot dQ \)
The result of the integration gives us the total work done, which is the energy (U) stored in the capacitor:
\(\displaystyle U = \frac{1}{2} \frac{Q^2}{C} \)
Since (Q = CV), we can substitute (Q) back into the energy equation to get it in terms of voltage:
\(\displaystyle U = \frac{1}{2} C V^2 \)
This formula tells us that the energy stored in a capacitor is directly proportional to the capacitance and the square of the voltage. It means that if you double the voltage, the energy goes up by four times, showing a strong voltage dependence.
Characteristics of Capacitors
Capacitors can store and release energy quickly. They also block direct current while allowing alternating current to pass.
Charge Storage: A capacitor is essentially a charge storage device. It consists of two plates separated by a dielectric material. When voltage is applied, one plate accumulates a positive charge while the other accumulates an equal amount of negative charge.
Dielectric Material: The dielectric material between the plates allows them to be at a high voltage without the charges arcing between them. This material also affects the capacitance by allowing more charge to be stored for a given voltage.
Capacitance: Capacitance is the measure of a capacitor’s ability to hold charge. It depends only on the geometry of the capacitor, such as the area of the plates and the distance between them.
Electric Field: The stored charge creates an electric field in the dielectric. This field is responsible for storing energy in the capacitor.
Charge and Voltage Relationship: The relationship between charge (Q) and voltage (V) in a capacitor is linear, described by the equation (Q = CV), where C is the capacitance.
Current Flow: While current can flow into and out of a capacitor, it does not flow across the dielectric from one plate to another. The plates do not touch, and the dielectric is an insulator.
Charge Distribution: The charges on the plates are distributed evenly due to their repulsion, and the thin, close plates allow for a strong electric field to be established, which helps in storing more charge.
Dielectric Constants: Different materials have different dielectric constants, which determine how much they can reduce the electric field for a given amount of charge. For example, glass has a dielectric constant of approximately 5.6, while water has a much higher constant of around 80.
Circuit Symbol: The electrical circuit symbol for a capacitor is two flat plates, representing the geometry of a typical capacitor, which often consists of two flat plates rolled into a cylindrical shape.
Energy Storage and Release: Capacitors can store and release energy quickly, making them useful in applications that require rapid changes in energy, like camera flashes or power stabilization in electronic devices.
What are Common Capacitors?
Common capacitors include ceramic, electrolytic, and tantalum capacitors. Here’s a table that categorizes common capacitors into fixed, variable, polarized, and non-polarized types.
| Type of Capacitor | Parent Category | Description | Common Uses | Key Characteristics |
|---|---|---|---|---|
| Ceramic Capacitors | Non-Polarized, Fixed | Made of ceramic dielectric; stable and versatile | RF circuits, audio systems | Small, wide capacitance range, non-polarized |
| Film Capacitors | Non-Polarized, Fixed | Use plastic film as the dielectric | Power supply filters, audio circuits | Stable, precise, low inductance |
| Electrolytic Capacitors | Polarized, Fixed | High capacitance, use an electrolyte | Power supplies, audio signal coupling | High capacitance-to-volume ratio, polarized |
| Tantalum Capacitors | Polarized, Fixed | A type of electrolytic with tantalum metal | Medical devices, military applications | Stable, reliable, long lifespan |
| Mica Capacitors | Non-Polarized, Fixed | Use mica as the dielectric | RF and microwave applications | High precision, reliable, excellent high-frequency characteristics |
| Paper Capacitors | Non-Polarized, Fixed | Made with paper as the dielectric | Historical electrical equipment, some power applications | Can handle high voltages, historical significance |
| Super Capacitors | Non-Polarized, Fixed | Also known as ultracapacitors, very high capacitance | Quick charging and discharging applications | Store a lot of energy, quick charge/discharge |
| Variable Capacitors | Variable | Capacitance can be adjusted | Radio tuning circuits | Used for tuning and calibration, adjustable capacitance |
Type of Capacitor
There are many types, such as fixed, variable, polarized, and non-polarized capacitors.
Fixed Capacitors
Fixed capacitors are components with a specific capacitance value that is determined during manufacturing and cannot be altered after production. They are designed to hold a set amount of electrical charge and are used in a wide range of electronic devices for various purposes.
The ability to store electrical charge, measured in farads (F), is fixed and does not change with the applied voltage. Consists of two metal plates (electrodes) separated by a dielectric material.
Includes polarized (like electrolytic capacitors) and non-polarized (such as ceramic, film, and mica capacitors). Used in filtering, timing circuits, power conditioning, and more.
Fixed capacitors are essential in circuits where a stable capacitance value is necessary for the device’s functionality. They come in various forms, each suited for specific applications based on their electrical characteristics.
Variable Capacitors
Variable capacitors are a type of capacitor whose capacitance can be intentionally and repeatedly changed. The capacitance of variable capacitors can be adjusted mechanically or electronically. They consist of two sets of plates: one fixed (stator) and the other movable (rotor).
By changing the effective area of overlap or the distance between the plates, you can alter the capacitance. Commonly used in L/C circuits to set the resonance frequency, like tuning a radio (hence sometimes called a tuning capacitor).
The most common form where a group of semicircular metal plates on a rotary axis are positioned in gaps between stationary plates. These materials are used as the dielectric between the plates. Achieved by “meshing” or “unmeshing” the plates, respectively.
Uses a set of concentric cylinder plates that can slide in or out, sealed in a vacuum to increase voltage handling capacity. The application of variable capacitors is to adjust the frequency to tune into different stations. And in antenna tuners to match the impedance of the antenna to the circuit. Variable capacitors are essential for fine-tuning electronic circuits, especially in applications where precise control of capacitance is necessary.
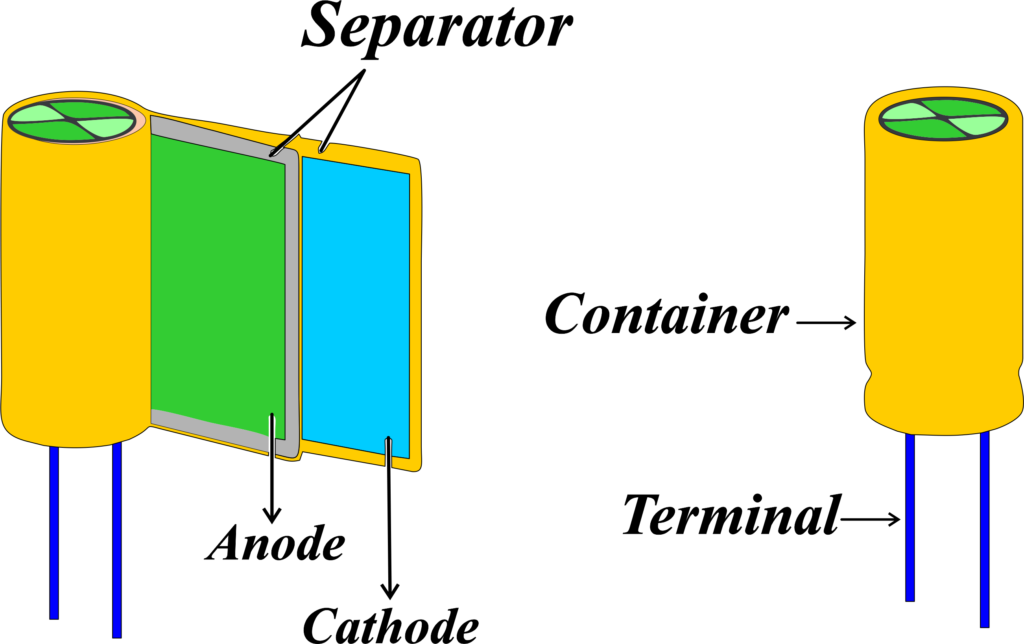
Polarized Capacitors
Polarized capacitors are a type of capacitor that have a designated positive and negative side, meaning they must be connected in a circuit with the correct orientation to work properly.
Polarized capacitors have a positive terminal (anode) and a negative terminal (cathode). The anode is typically made from a metal that forms an insulating oxide layer, which acts as the dielectric. The cathode is often a conductive material that serves as the electrolyte.
These capacitors can store a large amount of electrical energy relative to their size. These capacitors commonly used in power supply circuits for filtering and energy storage, and in audio equipment for signal coupling.
Examples:
- Electrolytic Capacitors: These include aluminum and tantalum capacitors, which are widely used due to their large capacitance values.
- Tantalum Capacitors: Known for their stability and reliability, often used in spaces where performance is critical.
Polarized capacitors are essential in many electronic devices, but they require careful handling and correct installation due to their polarity sensitivity.
Non-Polarized Capacitors
Non-polarized capacitors are a type of capacitor that do not have a designated positive or negative side, which means they can be connected in either direction in a circuit. They don’t have a specific positive or negative terminal, so there’s no need to worry about connecting them the wrong way.
Made with two conductive plates separated by a dielectric material like ceramic, paper, plastic film, air, or vacuum. Because they can be connected in any orientation, they’re used in a variety of circuits. Commonly found in circuits for coupling, decoupling, feedback, compensation, and oscillation.
Examples:
- Ceramic Capacitors: Often used for high-frequency applications like RF circuits and audio systems.
- Film Capacitors: Ideal for power supply filters and audio circuits due to their stability and low inductance.
Non-polarized capacitors are essential in electronics for applications that require flexibility in connection and where the polarity of the voltage may change or be undefined.
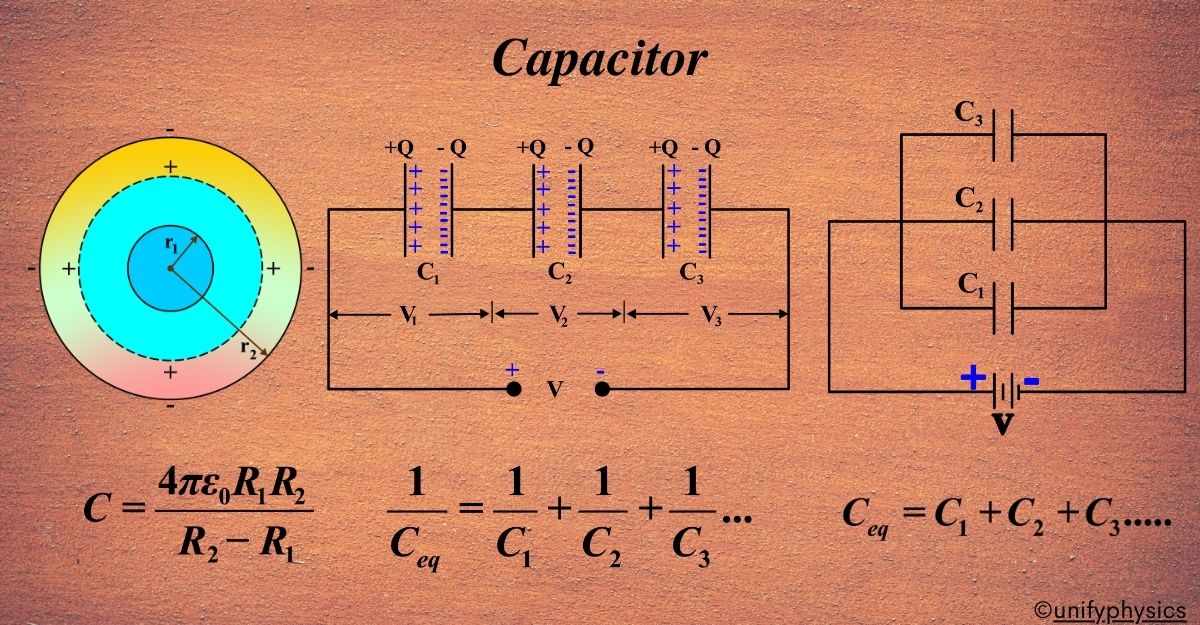
Parallel Combination of Capacitors
When capacitors are connected side by side, this is called a parallel combination. Here’s what’s unique about this setup: Each capacitor experiences the same voltage across its terminals. The total charge stored is the sum of the charges stored on each individual capacitor.

In a parallel circuit, the total capacitance (Ctotal) is simply the sum of the capacitances of each capacitor:
\(\displaystyle C_{total} = C_1 + C_2 + C_3 + … \)
where (C1, C2, C3, … ) are the capacitances of individual capacitors.
Adding capacitors in parallel gives you a higher total capacitance than any single capacitor alone. You can combine different capacitances to get a specific total value. If one capacitor fails, the others continue to work, which can be important in power supplies and other critical applications.
Think of a parallel combination of capacitors like multiple water tanks connected at the bottom. Each tank can be filled to the same level (voltage), and the total amount of water (charge) is the sum of the water in all tanks.
In a camera flash circuit, capacitors in parallel might be used to store a large amount of energy that can be released quickly to generate the flash of light.
Derivation of Parallel Combination of Capacitors:
Imagine you have several capacitors, and you connect them side by side, like books on a shelf. This is a parallel connection. In a parallel circuit, each capacitor is connected directly across the voltage source, so they all have the same voltage (V) across them.
Each capacitor will store its own charge based on its capacitance. Let’s say we have two capacitors, (C1) and (C2), the charge stored on each will be (Q1 = C1V) and (Q2 = C2V ) respectively.
The total charge (Qtotal) stored by the parallel combination is the sum of the individual charges:
\(\displaystyle Q_{total} = Q_1 + Q_2 \)
Substituting the charges, we get:
\(\displaystyle Q_{total} = C_1V + C_2V \)
The equivalent capacitance (Ceq) of the parallel combination is defined as the total charge divided by the voltage:
\(\displaystyle C_{eq} = \frac{Q_{total}}{V} \)
Substituting (Qtotal) from step 3, we get:
\(\displaystyle C_{eq} = \frac{C_1V + C_2V}{V} \)
Since (V) is common, it cancels out, leaving us with:
\(\displaystyle C_{eq} = C_1 + C_2 \)
For any number of capacitors connected in parallel, the total or equivalent capacitance (Ctotal) is just the sum of all the individual capacitances:
\(\displaystyle C_{total} = C_1 + C_2 + C_3 + … + C_n \)
where (C1, C2, C3, …, Cn) are the capacitances of each capacitor in the parallel circuit.
So, in a parallel circuit, it’s like adding more shelves to your bookshelf; you can store more books (charge). The more capacitors you add in parallel, the more charge you can store at the same voltage.
Series Combination of Capacitors
When capacitors are connected end-to-end, this is called a series combination. It’s like connecting batteries in a flashlight one after another. Each capacitor in a series holds the same amount of charge (Q). This is because the charge that accumulates on the plates of one capacitor must come from the plates of the adjacent one.
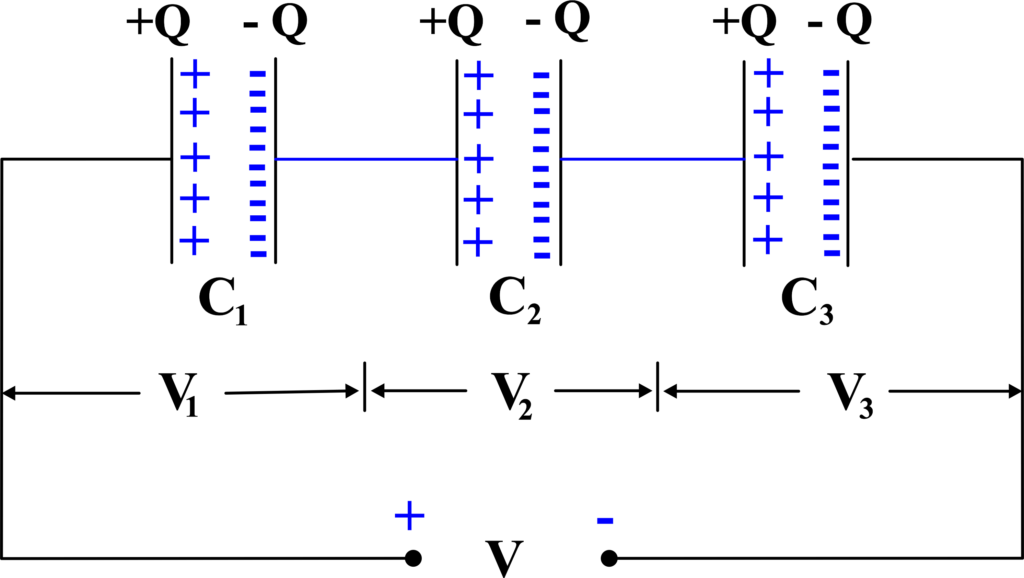
The total voltage (V) across the series combination is divided among the capacitors. If you have two capacitors, (C1) and (C2), with voltages (V1) and (V2) across them, the total voltage is the sum of these individual voltages:
\(\displaystyle V = V_1 + V_2 \)
For the series combination, the reciprocal of the total capacitance (\(\displaystyle\frac{1}{C_{total}} \)) is the sum of the reciprocals of the individual capacitances:
\(\displaystyle \frac{1}{C_{total}} = \frac{1}{C_1} + \frac{1}{C_2} + … + \frac{1}{C_n} \)
where (C1, C2, …, Cn ) are the capacitances of each capacitor in the series.
The total capacitance of a series combination is less than any individual capacitor’s capacitance in the series. Series combinations can handle higher voltages, as the voltage stress is divided among the capacitors.
Imagine a series of water pipes connected end-to-end with balloons inside them. When water flows, it fills the balloons equally. If one balloon represents a capacitor, all balloons (capacitors) have the same amount of water (charge), but the pressure (voltage) can be different across each one.
Example: In high-voltage applications, capacitors in series can be used to prevent any single capacitor from having too high a voltage across it, which could cause it to fail.
Derivation of Series Combination of Capacitors:
Imagine you have several capacitors, and you connect them one after another, like a train. This is a series connection. In a series circuit, each capacitor holds the same charge (Q). This is because the charge that leaves one plate of a capacitor must go onto the next.
The total voltage (V) across the series combination is the sum of the voltages across each individual capacitor. If we have two capacitors, (C1) and (C2), with voltages (V1) and (V2) across them, the total voltage is:
\(\displaystyle V = V_1 + V_2 \)
The voltage across each capacitor is related to the charge (Q) and its capacitance (C):
\(\displaystyle V_1 = \frac{Q}{C_1} \)
\(\displaystyle V_2 = \frac{Q}{C_2} \)
Substituting the voltages, we get:
$$ V = \frac{Q}{C_1} + \frac{Q}{C_2} $$
The equivalent capacitance (Ceq) of the series combination is defined as the total charge divided by the total voltage:
\(\displaystyle C_{eq} = \frac{Q}{V} \)
Substituting (V) from step 4 into the equation for (C_{eq} ), we get:
\(\displaystyle \frac{1}{C_{eq}} = \frac{1}{C_1} + \frac{1}{C_2} \)
General Formula
For any number of capacitors connected in series, the reciprocal of the total or equivalent capacitance ( \(\displaystyle\frac{1}{C_{total}}\) ) is the sum of the reciprocals of the individual capacitances:
\(\displaystyle \frac{1}{C_{total}} = \frac{1}{C_1} + \frac{1}{C_2} + … + \frac{1}{C_n} \)
where (C1, C2, …, Cn ) are the capacitances of each capacitor in the series circuit.
So, in a series circuit, it’s like having a single capacitor whose capacitance is less than any of the individual capacitors in the series. This is because the charge has to ‘squeeze’ through each capacitor, which effectively reduces the total capacitance.
Capacitance of a Spherical Capacitor
Imagine two hollow, metallic balls, one inside the other, with a bit of space between them. This is a spherical capacitor. The inner ball is one plate, and the outer ball is the other plate.
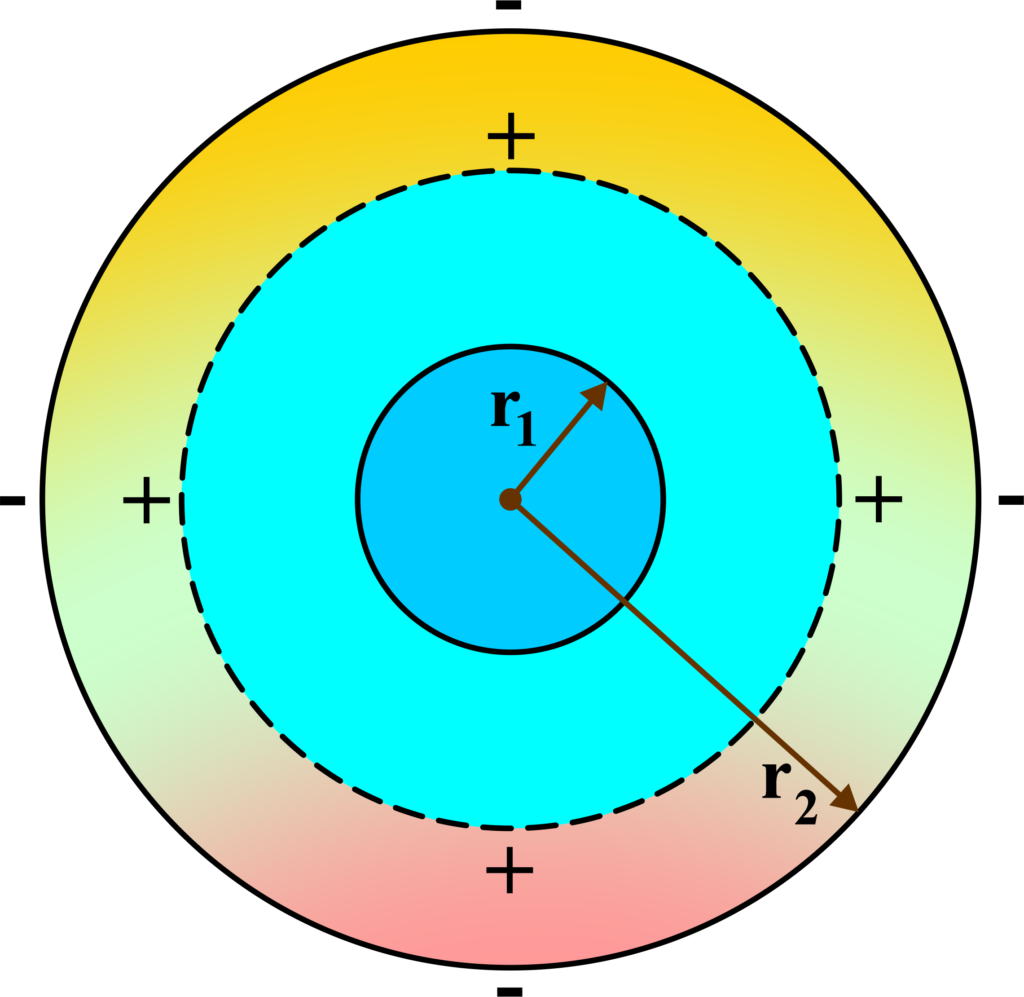
When you charge a spherical capacitor, the inner sphere gets one type of charge (say, positive), and the outer sphere gets the opposite charge (negative). This setup creates an electric field in the space between the spheres, which stores energy.
The capacitance (C) of a spherical capacitor depends on the radii of the inner (r1) and outer (r2) spheres and the permittivity of free space (\(\displaystyle\epsilon_0 \)):
\(\displaystyle C = \frac{4\pi\epsilon_0 r_1 r_2}{r_2 – r_1} \)
This formula tells us how much charge the capacitor can store for a given voltage. If the spheres are larger, the capacitance increases because there’s more ‘room’ to store charge. If the spheres are closer together (small ( r2 – r1 )), the capacitance increases because the electric field is stronger.
Think of the spherical capacitor like a snow globe. The inner sphere is like the figure in the middle, and the outer sphere is the globe itself. The space between them is where the ‘magic’ (electric field) happens when you shake it (apply voltage).
Derivation of Capacitance of a Spherical Capacitor:
A spherical capacitor consists of two concentric spherical conductors: an inner sphere with radius (r1) and an outer sphere with radius (r2). The space between the two spheres is filled with a dielectric material.
Let’s give the inner sphere a charge (+Q) and the outer sphere a charge (-Q). Using Gauss’s Law, the electric field ( E ) at a distance ( r ) from the center (where (r1 < r < r2) is given by:
\(\displaystyle E = \frac{Q}{4\pi\epsilon_0 r^2} \) …….(1)
Here, ( \(\displaystyle\epsilon_0 \)) is the permittivity of free space.
The potential difference (V) between the two spheres is the integral of the electric field over the distance from (r1) to (r2):
\(\displaystyle V = \int_{r_1}^{r_2} E \, dr \)
Substituting (E) from eq. 1, we get:
\(\displaystyle V = \int_{r_1}^{r_2} \frac{Q}{4\pi\epsilon_0 r^2} \, dr \)
Solving this integral, we find:
\(\displaystyle V = \frac{Q}{4\pi\epsilon_0} \left( \frac{1}{r_1} – \frac{1}{r_2} \right) \)
Capacitance is defined as the charge stored per unit potential difference, so:
\(\displaystyle C = \frac{Q}{V} \) ………(2)
Substituting (V) from eq. 2, we get:
\(\displaystyle C = \frac{Q}{\frac{Q}{4\pi\epsilon_0} \left( \frac{1}{r_1} – \frac{1}{r_2} \right)} \)
Simplifying this, we find the expression for the capacitance of a spherical capacitor:
\(\displaystyle C = 4\pi\epsilon_0 \frac{r_1 r_2}{r_2 – r_1} \)
The capacitance of a spherical capacitor depends on the radii of the inner and outer spheres and the permittivity of the material between them. It tells us how much charge the capacitor can store for a given potential difference.
What happens if the radii of the spheres change?
When the radii of the spheres in a spherical capacitor change, it affects the capacitance of the capacitor.
Increasing the Inner Radius (r1): If you increase the inner radius while keeping the outer radius (r2) constant, the capacitance decreases. This is because the area available for charge storage on the inner sphere increases, but the distance between the two spheres also increases, which reduces the capacitance.
Increasing the Outer Radius (r2): If you increase the outer radius, the capacitance decreases as well. This happens because the distance between the two spheres increases, which weakens the electric field and reduces the capacitance.
Decreasing the Distance Between the Spheres: If the difference between the radii (r2 – r1) is decreased (meaning the spheres are closer together), the capacitance increases. A smaller distance between the spheres strengthens the electric field between them, allowing more charge to be stored for the same voltage, thus increasing the capacitance.
The capacitance of a spherical capacitor is sensitive to changes in the radii of the spheres. It’s all about the balance between the area available for charge storage and the distance over which the electric field is established.
Applications of Capacitors
Capacitors are like the Swiss Army knives of the electronic world because they have so many different uses.
Energy Storage: Capacitors store electrical energy when connected to a power source. In a camera flash, the capacitor stores energy and then releases it quickly to produce the flash.
Power Conditioning: They help maintain a steady voltage level in power supplies. In computers, capacitors smooth out the output of power supplies to prevent damage to sensitive components.
Signal Filtering: Capacitors can filter out certain frequencies from an electrical signal. In audio equipment, they’re used to filter out noise, ensuring clear sound quality.
Timing Circuits: When combined with resistors, capacitors can create specific time delays. They’re used in blinking LED circuits, where the capacitor charges and discharges at regular intervals to turn the LED on and off.
Touch Screens: Capacitors can detect changes in capacitance when a finger is near the screen. Smartphones and tablets use capacitors to detect touch inputs.
Motor Starters: Capacitors provide an initial surge of energy to start electric motors. In air conditioners, capacitors help start the compressor motor.
Energy Storage in Defibrillators: They store the charge needed to deliver a life-saving electric shock. Heart defibrillators use capacitors to store energy that is then released to correct heart arrhythmias.
Also Read: Parallel Plate Capacitor
Solved Examples
Problem 1: A capacitor of capacitance (10 µF) is connected to a (12V) battery. Calculate the energy stored in the capacitor.
Solution: The energy (U) stored in a capacitor is given by:
\(\displaystyle U = \frac{1}{2} C V^2 \)
Given: \(\displaystyle C = 10 \, \mu\text{F} = 10 \times 10^{-6} \, \text{F} \); V = 12 V
Calculate (U):
\(\displaystyle U = \frac{1}{2} \times 10 \times 10^{-6} \times (12)^2 \)
\(\displaystyle U = \frac{1}{2} \times 10 \times 10^{-6} \times 144 \)
\(\displaystyle U = 5 \times 10^{-6} \times 144 \)
\(\displaystyle U = 720 \times 10^{-6} \)
\(\displaystyle U = 7.2 \times 10^{-4} \, \text{J} \)
Therefore, the energy stored in the capacitor is (\(\displaystyle 7.2 \times 10^{-4} \, \text{J} \)).
Problem 2: Two capacitors, (C1 = 4 µF) and (C2 = 6 µF), are connected in parallel. Calculate the equivalent capacitance.
Solution: For capacitors in parallel, the equivalent capacitance (Ceq) is the sum of the individual capacitances:
\(\displaystyle C_{\text{eq}} = C_1 + C_2 \)
Given: C1 = 4 µF ; C2 = 6 µF
Calculate (Ceq):
\(\displaystyle C_{\text{eq}} = 4 + 6\)
\(\displaystyle C_{\text{eq}} = 10 \, \mu\text{F} \)
Therefore, the equivalent capacitance is 10 µF.
Problem 3: Two capacitors, (C1 = 3 µF) and (C2 = 6 µF), are connected in series. Calculate the equivalent capacitance.
Solution: For capacitors in series, the reciprocal of the equivalent capacitance (\(\displaystyle \frac{1}{C_{\text{eq}}} \)) is the sum of the reciprocals of the individual capacitances:
\(\displaystyle \frac{1}{C_{\text{eq}}} = \frac{1}{C_1} + \frac{1}{C_2} \)
Calculate ( \(\displaystyle\frac{1}{C_{\text{eq}}} \)):
\(\displaystyle \frac{1}{C_{\text{eq}}} = \frac{1}{3} + \frac{1}{6} \)
\(\displaystyle \frac{1}{C_{\text{eq}}} = \frac{2}{6} + \frac{1}{6} \)
\(\displaystyle \frac{1}{C_{\text{eq}}} = \frac{3}{6} \)
\(\displaystyle\frac{1}{C_{\text{eq}}} = \frac{1}{2} \)
Therefore, the equivalent capacitance is:
\(\displaystyle C_{\text{eq}} = 2 \, \mu\text{F} \)
Problem 4: Calculate the capacitance of a spherical capacitor consisting of two concentric spherical shells with radii (R1 = 10 cm) and (R2 = 20 cm). The space between the shells is vacuum.
Solution: The capacitance (C) of a spherical capacitor is given by:
\(\displaystyle C = 4 \pi \epsilon_0 \frac{R_1 R_2}{R_2 – R_1} \)
Given: \(\displaystyle \epsilon_0 = 8.854 \times 10^{-12} \, \text{F/m} \)
Calculate (C):
\(\displaystyle C = 4 \pi \times 8.854 \times 10^{-12} \frac{0.1 \times 0.2}{0.2 – 0.1} \)
\(\displaystyle C = 4 \pi \times 8.854 \times 10^{-12} \frac{0.02}{0.1} \)
\(\displaystyle C = 4 \pi \times 8.854 \times 10^{-12} \times 0.2 \)
\(\displaystyle C = 8.854 \times 10^{-12} \times 0.8 \pi \)
\(\displaystyle C \approx 2.22 \times 10^{-11} \, \text{F}\)
Therefore, the capacitance of the spherical capacitor is approximately ( 22.2 pF).
Problem 5: Two capacitors, (C1 = 5 µF) and (C2 = 10 µF), are connected in parallel and charged to a potential difference of (20 V). Calculate the total energy stored in the combination.
Solution: The total energy stored (U) in a parallel combination of capacitors is the sum of the energies stored in each capacitor:
\(\displaystyle U = \frac{1}{2} C_1 V^2 + \frac{1}{2} C_2 V^2 \)
Calculate (U):
\(\displaystyle U = \frac{1}{2} \times 5 \times 10^{-6} \times (20)^2 + \frac{1}{2} \times 10 \times 10^{-6} \times (20)^2 \)
\(\displaystyle U = \frac{1}{2} \times 5 \times 10^{-6} \times 400 + \frac{1}{2} \times 10 \times 10^{-6} \times 400 \)
\(\displaystyle U = 1 \times 10^{-3} + 2 \times 10^{-3} \)
\(\displaystyle U = 3 \times 10^{-3} \, \text{J} \)
Therefore, the total energy stored in the parallel combination of capacitors is (\(\displaystyle 3 \times 10^{-3} \, \text{J} \)).
Problem 6: Two capacitors, (C1 = 2 µF) and (C2 = 4 µF), are connected in series and charged to a potential difference of (30 V). Calculate the total energy stored in the combination.
Solution: First, calculate the equivalent capacitance (Ceq) for the series combination:
\(\displaystyle \frac{1}{C_{\text{eq}}} = \frac{1}{C_1} + \frac{1}{C_2} \)
\(\displaystyle \frac{1}{C_{\text{eq}}} = \frac{1}{2} + \frac{1}{4} \)
\(\displaystyle \frac{1}{C_{\text{eq}}} = \frac{2}{4} + \frac{1}{4} \)
\(\displaystyle \frac{1}{C_{\text{eq}}} = \frac{3}{4} \)
\(\displaystyle C_{\text{eq}} = \frac{4}{3} \, \mu\text{F} = 1.333 \times 10^{-6} \, \text{F} \)
The energy (U) stored in the equivalent capacitor is:
\(\displaystyle U = \frac{1}{2} C_{\text{eq}} V^2 \)
Given: \(\displaystyle C_{\text{eq}} = 1.333 \times 10^{-6} \, \text{F} \) ; V = 30 V
Calculate (U):
\(\displaystyle U = \frac{1}{2} \times 1.333 \times 10^{-6} \times (30)^2 \)
\(\displaystyle U = \frac{1}{2} \times 1.333 \times 10^{-6} \times 900 \)
\(\displaystyle U = 0.6665 \times 10^{-3} \times 900 \)
\(\displaystyle U = 0.59985 \times 10^{-3} \, \text{J} \)
\(\displaystyle U \approx 0.6 \times 10^{-3} \, \text{J} \)
Therefore, the total energy stored in the series combination of capacitors is (\(\displaystyle 0.6 \times 10^{-3} \, \text{J} \)).
FAQs
What is a capacitor and how does it work?
A capacitor is an electrical component that stores energy in the form of an electric field between two conductive plates separated by an insulating material (dielectric). When a voltage is applied across the plates, an electric charge accumulates on the plates, creating a potential difference and storing energy.
How is energy stored in a capacitor?
Energy is stored in a capacitor by accumulating electric charges on its plates when a voltage is applied. This stored energy can be released when needed, making capacitors useful in various applications like power supplies, signal processing, and electronic circuits.
What happens when capacitors are connected in parallel?
When capacitors are connected in parallel, the total capacitance increases. Each capacitor stores charge independently, and the total charge stored is the sum of the charges on each capacitor. This configuration is useful for increasing the overall capacitance in a circuit.
How does the series combination of capacitors affect the total capacitance?
In a series combination of capacitors, the total capacitance decreases. The reciprocal of the total capacitance is the sum of the reciprocals of the individual capacitances. This configuration is used when a lower total capacitance or a higher voltage rating is needed.
What is the significance of the capacitance of a spherical capacitor?
The capacitance of a spherical capacitor, which consists of two concentric spherical conducting shells, is significant in understanding how capacitors store energy in a spherical geometry. This type of capacitor is useful in various scientific and engineering applications, including spherical storage devices and certain types of sensors.
How does the dielectric material affect the capacitance of a capacitor?
The dielectric material between the plates of a capacitor affects its capacitance by increasing the capacitor’s ability to store charge. A dielectric material increases the capacitance by reducing the electric field strength for the same amount of charge, thus allowing more charge to be stored for a given voltage.
Why are capacitors important in electronic circuits?
Capacitors are important in electronic circuits for several reasons: they store and release energy, filter signals, smooth out voltage fluctuations, and provide timing elements in oscillators and timers. Their ability to quickly charge and discharge makes them essential components in power supplies, signal processing, and many other electronic applications.