Capillary Rise

The concept of capillary action dates back to the Renaissance period. The first recorded observation of this phenomenon was by none other than the polymath Leonardo da Vinci. His curiosity and keen observation skills led him to notice how water could defy gravity and climb up narrow spaces.

Fast forward to the 17th century, and we find the Irish chemist Robert Boyle—famous for Boyle’s law—puzzled by the ascent of water in capillary tubes. He reported that “some inquisitive French Men” had observed water rising to a certain height in a tube, which was not influenced by a vacuum, suggesting that this was a different phenomenon from what governed mercury barometers.

Several scientists, including Francis Hauksbee, Jacob Bernoulli, and Giovanni Alfonso Borelli, contributed to the understanding of capillary action. They had different theories, from air pressure differences to the attraction between liquid particles and the walls of the capillary.

An English physician named James Jurin is credited with establishing the mathematical relationship between the height of the liquid and the radius of the capillary, known as Jurin’s Law. This was a significant step forward in quantifying the observations made by his predecessors.

Today, we understand capillary action as a balance of cohesive and adhesive forces, along with surface tension. These forces allow liquids to move through narrow spaces without the assistance of, and sometimes in opposition to, external forces like gravity.

What Is Capillary Rise?

Capillary rise is a phenomenon that occurs when a liquid climbs up a narrow tube or space without the assistance of, and in opposition to, external forces like gravity. In simpler terms, it’s how a liquid can climb up a narrow tube on its own. This happens due to the interplay between two main types of forces: cohesive forces (the attraction between like molecules within the liquid) and adhesive forces (the attraction between the liquid molecules and the molecules of the tube’s surface).

• Adhesion and Cohesion: When you place a narrow glass tube (a capillary) into a container of water, the water molecules are attracted to the glass (adhesive force) more than they are attracted to each other (cohesive force). This causes the water to climb up the walls of the tube.
• Surface Tension: Surface tension, a result of cohesive forces among the liquid molecules, acts to minimize the surface area of the liquid. In the capillary, this helps pull the liquid column upwards.
• Balancing Forces: The liquid continues to rise until the upward adhesive force is balanced by the weight of the liquid column being pulled up by gravity.

The height (h) to which a liquid will rise or fall in a capillary tube can be calculated using the formula:

\(\displaystyle\begin{equation}\label{eqn:1}\boxed{\boldsymbol{ h = \frac{2 \sigma \cos \theta}{\rho g r}}} \end{equation}\)

• (σ) is the surface tension of the liquid.
• (θ) is the contact angle.
• (ρ) is the density of the liquid.
• (g) is the acceleration due to gravity.
• (r) is the radius of the capillary tube.

Example: Imagine you’re using a thin straw to sip a drink. Have you noticed how the liquid seems to climb up the straw a bit, even before you start sipping? That’s capillary action at work!

Capillary Rise is a fascinating natural phenomenon where a liquid spontaneously rises in a narrow tube or capillary. Here’s how it happens:

• Tiny Tubes: First, think of capillaries as really tiny straws. The smaller the diameter, the more noticeable the effect.
• Climbing Liquid: When part of the capillary is dipped in a liquid, the liquid starts to climb up the walls of the tube. This happens because the molecules of the liquid are attracted to the tube’s material—a force we call adhesion.
• Sticking Together: The liquid molecules also like to stick to each other, thanks to a force called cohesion. But in the case of capillary rise, adhesion is stronger than cohesion, which pulls the liquid up along the tube wall.
• Surface Tension: As the liquid rises, the surface of the liquid inside the tube forms a curve. This curve is held together by surface tension, which tries to minimize the surface area of the liquid.
• Balancing Act: The liquid keeps rising until the weight of the liquid column is balanced by the upward force caused by surface tension and adhesion.

Factors Affecting Capillary Rise:

Diameter of the Tube: The narrower the tube, the higher the liquid will rise. This is because the adhesive force acting on a smaller cross-sectional area can lift the liquid higher.

Surface Tension: Liquids with higher surface tension will rise more in a capillary tube. For instance, water, which has relatively high surface tension, exhibits a noticeable capillary rise.

Contact Angle: This is the angle between the tangent to the liquid surface and the solid surface at the point of contact. A smaller contact angle (which happens when the liquid wets the surface well) results in a higher capillary rise.

Density of the Liquid: Denser liquids will rise less in the capillary tube because their weight counteracts the adhesive force more effectively.

In simple terms, Capillary Rise is like a tug-of-war between the forces of adhesion, cohesion, and gravity. The liquid climbs up the tube as if it’s trying to escape, but only goes as high as the balance of forces allows. This is why plants can transport water from their roots to their leaves, and why a paper towel can soak up a spill. It’s all about the incredible balancing act of forces in nature!

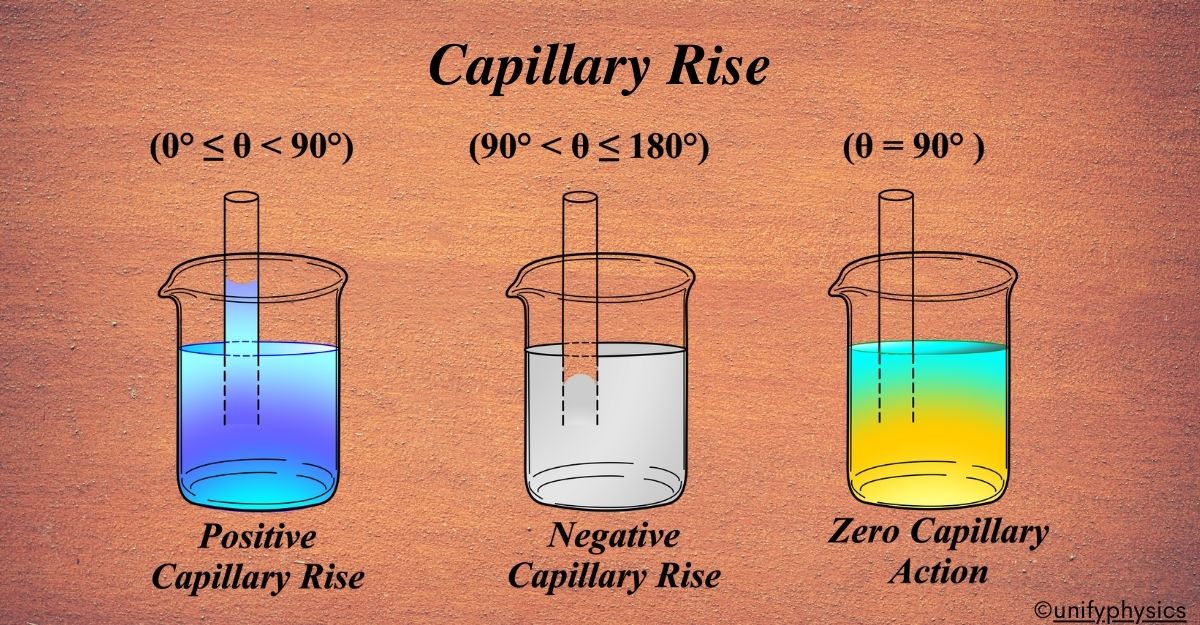
Capillary Rise

The phenomenon of capillary rise or fall is heavily influenced by the angle of contact between the liquid and the tube. This angle determines whether the liquid will rise, fall, or remain flat within the capillary tube. Let’s explore how this works for different scenarios.

The contact angle (θ) is the angle formed between the tangent to the liquid surface at the point of contact with the solid surface (capillary tube) and the solid surface itself.

Positive Capillary Rise \(\displaystyle( 0^\circ \leq \theta < 90^\circ \)):

When the contact angle is less than 90 degrees, the liquid wets the surface of the tube, and the adhesive forces between the liquid and the tube are stronger than the cohesive forces within the liquid. Example: Water in a glass tube.

• The liquid rises up the tube, forming a concave meniscus. The height (h) is positive.
• The upward adhesive force is stronger, pulling the liquid up until balanced by gravity.

Negative Capillary Fall \(\displaystyle ( 90^\circ < \theta \leq 180^\circ \)):

When the contact angle is greater than 90 degrees, the liquid does not wet the surface of the tube, and the cohesive forces within the liquid are stronger than the adhesive forces between the liquid and the tube. Example: Mercury in a glass tube.

• The liquid falls within the tube, forming a convex meniscus. The height (h) is negative.
• The downward cohesive force is stronger, causing the liquid to be depressed until balanced by the atmospheric pressure.

Zero Capillary Action (\(\displaystyle\theta = 90^\circ \)):

When the contact angle is exactly 90 degrees, the adhesive and cohesive forces are balanced in such a way that there is no net capillary action. Example: Hypothetical situation with perfectly balanced forces.

• The liquid level inside the capillary tube remains the same as the liquid level outside. The meniscus is flat, and the height (h) is zero.
• The forces are perfectly balanced, resulting in no rise or fall of the liquid.

Forces in Capillary Rise

Adhesive force: The attraction between the liquid molecules and the tube’s surface. Imagine you have a piece of tape. When you stick it to a wall, it stays put because of the attraction between the tape and the wall. This attraction is what we call an adhesive force. It’s the same kind of force that makes a post-it note stick to your notebook.

Now, let’s apply this to capillary rise. When you dip a narrow tube into the water, the water doesn’t just sit at the bottom; it starts to climb up the walls of the tube. This happens because the water molecules are attracted to the glass molecules of the tube more than they are to each other. This attraction between the water and the glass is, again, the adhesive force at work.

The adhesive force is crucial because it’s the initial “pull” that starts the capillary action. Without this force, the liquid wouldn’t rise at all. It’s like the first step in a staircase that leads to the rest of the capillary journey.

To help visualize it, think of the water molecules as tiny climbers and the glass tube as a cliff face. The climbers (water molecules) use their hands (adhesive force) to grab onto the cliff (tube) and pull themselves up.

In capillary rise, the adhesive force is responsible for:

• Pulling the liquid against gravity.
• Forming the meniscus (the curve you see at the top of the liquid in the tube).
• Determining the height to which the liquid will rise (along with other factors like tube diameter and liquid properties).

So, in summary, the adhesive force is like the unsung hero of capillary action. It’s the force that starts the whole process, allowing liquids to move in ways that are essential for nature and technology, like how trees get water from their roots to their leaves.

Cohesive force: The attraction between the liquid molecules themselves. Think of cohesive force like a team sport, where all players are holding hands to stay together. In the world of molecules, cohesive force is the “hand-holding” between similar molecules. It’s the force that makes water droplets form and allows liquids to flow smoothly.

When you pour water into a glass, it doesn’t just splatter into a messy puddle; it stays together as a liquid. That’s a cohesive force in action—water molecules are attracted to each other, keeping the liquid intact.

Now, when it comes to capillary rise, cohesive force plays a balancing role. While adhesive force pulls the liquid up the tube, cohesive force tries to keep the liquid together, preventing it from breaking apart as it rises.

In capillary action, there’s a delicate balance between the adhesive force (pulling the liquid up the tube) and the cohesive force (keeping the liquid together). If the cohesive force is too strong, the liquid won’t rise much. If it’s just right, the liquid can climb up the tube like a skilled acrobat.

To help students visualize, you can compare cohesive force to a group of friends in a tug-of-war game. They need to hold on to each other tightly to move as one unit. Similarly, molecules need cohesive force to move together through a capillary tube.

In capillary rise, cohesive force is responsible for:

• Maintaining the integrity of the liquid column as it rises.
• Influencing the shape of the meniscus (the curve at the top of the liquid).
• Determining the maximum height the liquid can reach before the weight of the liquid column overcomes the cohesive force.

So, cohesive force is like the glue that holds the liquid together, allowing it to perform the amazing feat of capillary rise. Without cohesive force, liquids wouldn’t be liquids, and many natural processes, like rain formation and blood circulation, would be impossible.

Surface Tension: The elastic tendency of a fluid surface which makes it acquire the least surface area possible. Imagine you’re gently placing a paper clip on the surface of water. It floats, right? That’s because of surface tension. It’s like the water has an invisible skin on top that’s holding the paper clip up.

In capillary rise, surface tension is the hero that pulls the liquid up against gravity. It’s the force that acts along the surface of the liquid and tries to minimize the surface area.

When a capillary tube is dipped into a liquid, the liquid rises or falls inside the tube. This happens because the molecules at the surface of the liquid are pulling on each other with a force we call surface tension.

Surface tension is responsible for:

• Creating the meniscus (the curved surface of the liquid in the tube).
• Pulling the liquid up the tube in capillary action.
• Balancing the forces of gravity determines how high the liquid will rise.

The surface tension acts along the circumference of the tube, pulling the liquid up. It’s like a team of ants pulling on a leaf to lift it off the ground. Each ant (molecule) is pulling with a tiny force, but together, they can do something amazing—like lifting a leaf or, in our case, making water climb a tube!

The height to which the liquid rises is given by the formula:

\(\displaystyle h = \frac{2 \sigma}{\rho r g} \)

where (h) is the height, (σ) is the surface tension, (ρ) is the density of the liquid, (r) is the radius of the tube, and (g) is the acceleration due to gravity.

Surface tension is a powerful force that’s not just about floating paper clips. It’s a fundamental force in nature that allows liquids to perform incredible feats, like climbing up tiny tubes in capillary action.

Remember, surface tension is the force that’s working hard to keep the surface of liquids as small as possible, and it’s this force that enables the amazing phenomenon of capillary rise.

Also Read: Angle Of Contact

Equation Of Capillary Rise

Capillary rise occurs when a liquid moves up a narrow tube against gravity. This happens because of surface tension and the forces between the liquid and the tube’s surface.

The height (h) to which the liquid rises is given by the formula:

\(\displaystyle h = \frac{2\sigma \cos \theta}{\rho gr} \)

Surface tension (σ) acts along the circumference of the tube, trying to minimize the surface area. The force due to surface tension is

\(\displaystyle F_{\text{surface tension}} = \sigma \times (2\pi r) \hspace{1cm} (1)\)

The weight of the liquid column that rises in the tube is

\(\displaystyle W = \rho \times V \times g \hspace{1cm} (2)\)

where (V) is the volume of the liquid column. The volume (V) is the area of the cross-section of the tube times the height (h) the liquid rises, so

\(\displaystyle V = \pi r^2 \times h \hspace{1cm} (3)\).

For the liquid to be in equilibrium, the upward force due to surface tension must balance the downward force due to weight. So,

\(\displaystyle F_{\text{surface tension}} = W \).

Substituting the values from steps 1 and 3 into the equation from step 4, we get:

\(\displaystyle\sigma \times (2\pi r) = \rho \times (\pi r^2 \times h) \times g\)

Simplifying the equation, we cancel out \(\displaystyle \pi \) and one (r), and we get:

\(\displaystyle h = \frac{2\sigma}{\rho gr}h\)

The actual height also depends on the angle of contact (θ). When the angle is taken into account, the effective radius becomes (rcosθ), leading to the final formula:

\(\displaystyle h = \frac{2\sigma \cos \theta}{\rho gr}h\)

The capillary rise formula shows how the height to which a liquid rises in a tube depends on the surface tension, the angle of contact, the density of the liquid, the acceleration due to gravity, and the radius of the tube.

Dependency of Capillary Rise

Capillary Rise is like a magic trick where water climbs up a narrow tube all by itself. But this “magic” depends on several factors:

• Tube Radius: The narrower the tube, the higher the water climbs. It’s like climbing a ladder—the narrower the ladder, the closer you can get to the walls, and the higher you can go.
• Surface Tension: This is the “strength” of the water’s surface. The stronger the surface tension, the more the water can pull itself up the tube.
• Density of the Liquid: Heavier liquids have a harder time climbing. It’s like carrying a heavy backpack—the heavier it is, the harder it is to climb.
• The angle of Contact: This is how the water “touches” the tube. If the water spreads out nicely, it can climb higher. It’s like having good grip shoes—the better the grip, the higher you can climb.

The height to which the liquid rises (h) in a capillary tube can be calculated using the formula:

\(\displaystyle h = \frac{2 \sigma \cos(\theta)}{\rho r g} \)

If you want to see a higher capillary rise, use a super narrow tube, with a liquid that has strong surface tension, is not too dense, and wets the tube well (small angle of contact). It’s like having the perfect conditions for climbing a wall without any tools—just the right shoes, strength, and a good grip!

Liquid Meniscus in Capillarity

The meniscus is the curve at the top of a liquid in response to its container. In capillarity, the meniscus can be either concave or convex, depending on the liquid and the surface. When you fill a glass with water, have you noticed that the water’s surface isn’t flat? It curves near the edges, forming what we call a meniscus. This curve is more pronounced in a narrow tube, like a capillary tube, and it’s a key part of capillarity.

The meniscus forms because of the tug-of-war between two forces: Adhesion: The attraction between the liquid molecules and the tube’s material. Cohesion: The attraction between the liquid molecules themselves.

Types of Meniscus: Depending on the liquid and the material of the tube, the meniscus can be:

Concave Meniscus

It is curving upward, like water in a glass tube. This happens when adhesion is stronger than cohesion. When you fill a capillary tube with water, you’ll notice that the water doesn’t just form a flat surface. Instead, it curves upwards, creating what we call a concave meniscus. This is the most common type of meniscus that students will encounter, especially with water.

The concave meniscus occurs because the water molecules are more attracted to the glass walls of the tube than they are to each other. This attraction to the glass is due to the adhesive forces at play. Because of these forces, the water “climbs” up the sides of the tube, creating that curved shape.

To help students visualize, think of the water molecules as little climbers with tiny hands. These climbers are reaching out and grabbing onto the walls of the tube. The stronger their grip (adhesion), the higher they pull themselves up, and the more pronounced the concave shape becomes.

Surface tension also plays a role here. It acts like an elastic band stretched across the opening of the tube, pulling the surface of the water into the lowest possible area. This tension, combined with the adhesive forces, results in the concave meniscus.

In the lab, when measuring liquids in a graduated cylinder or pipette, it’s important to read the volume at the lowest point of the concave meniscus. This ensures accuracy in measurements, as the concave shape can affect the perceived level of the liquid.

The concave meniscus is a perfect example of how different forces interact with each other. It’s not just a curve in the water; it’s a demonstration of adhesive forces overcoming cohesive forces, with surface tension pulling it all together into a shape that minimizes energy.

Convex Meniscus

It is curving downward, like mercury in a glass tube. This occurs when cohesion is stronger than adhesion. A convex meniscus is what you see when certain liquids, like mercury, are placed in a glass tube. Instead of curving up as water does, mercury curves downward, making a dome-like shape that’s higher in the middle than at the edges.

The reason behind this downward curve is all about the forces between the molecules: Cohesive force: This is the force between mercury molecules. It’s very strong, meaning mercury molecules really like to stick together. Adhesive force: This is the force between mercury molecules and the glass tube. It’s weaker than the cohesive force in this case. Because the cohesive force is stronger, the mercury molecules don’t spread out and climb up the walls of the tube. Instead, they stick together, forming a convex shape.

Imagine a group of people (mercury molecules) huddled together in the center of a room (the tube). They prefer to stay close to each other rather than spread out and touch the walls. This is similar to how mercury forms a convex meniscus.

Surface tension still plays a role here. It pulls the mercury into the shape that has the least surface area for its volume—a dome or convex shape. It’s like a stretched balloon; it naturally forms a rounded shape because that’s the shape with the least amount of surface.

The convex meniscus is a great example of how different forces can shape the behavior of liquids. In the case of mercury, the strong attraction between its own molecules creates a dome-like meniscus, showing us that not all liquids behave the same way when they come into contact with solid surfaces.

Plane Meniscus

A plane meniscus is what you get when the forces of cohesion (which pull the liquid molecules together) and adhesion (which attract the liquid to the container walls) are perfectly balanced. Unlike the curved surfaces of concave or convex menisci, a plane meniscus is flat and level.

A plane meniscus occurs when the liquid neither climbs up the walls of the container (like water in a glass tube) nor dips down (like mercury in a glass tube). This happens when the angle of contact between the liquid and the container is exactly 90 degrees.

Think of a plane meniscus like a calm lake. The surface of the lake is flat because the forces acting on it are in equilibrium. There’s no wind (adhesive force) pushing the water to form waves (concave or convex meniscus), and the water’s own weight (cohesive force) is evenly distributed.

In capillarity, a plane meniscus is a special case. It indicates that the liquid is not wetting the tube (no capillary rise) nor is it being repelled (no capillary depression). It’s a neutral situation where the liquid’s surface tension is in perfect harmony with the forces exerted by the container’s walls.

The plane meniscus is a great example of balance in nature. It shows us that when forces are perfectly matched, the result is a stable, level surface. Understanding this helps students appreciate the delicate interplay of forces that govern the behavior of liquids in different situations.

Relationship between Excess Pressure and Surface Tension

Let’s imagine a liquid drop. It’s like a tiny, round balloon filled with water. The surface of this drop is under tension, just like the stretched rubber of a balloon. This tension on the surface is what we call surface tension.

Now, because the surface is stretched, there’s a pressure inside the drop that’s trying to push out. This pressure is higher than the pressure outside the drop. We call this extra pressure the excess pressure.

The force due to surface tension acts all around the circumference of the drop. If we denote surface tension by (σ), and the circumference by (C), then the total force due to surface tension is

\(\displaystyle F_{\text{surface tension}} = \sigma \times C \).

For a spherical drop, the circumference is the same as the equator’s length, which is

\(\displaystyle C = 2\pi r \),

where (r) is the radius of the drop. Substituting the circumference into the first equation, we get

\(\displaystyle F_{\text{surface tension}} = \sigma \times 2\pi r \).

The excess pressure inside the drop exerts a force over the cross-sectional area of the drop. If (P) is the excess pressure, then the force is

\(\displaystyle F_{\text{excess pressure}} = P \times A \),

where (A) is the area, \(\displaystyle A = \pi r^2 \). For the drop to be stable, the force due to surface tension must balance the force due to excess pressure. So, we set them equal to each other:

\(\displaystyle \sigma \times 2\pi r = P \times \pi r^2 \)

To find the excess pressure, we divide both sides by \(\displaystyle \pi r^2 \):

\(\displaystyle P = \frac{\sigma \times 2\pi r}{\pi r^2} \)

Simplifying the equation, we cancel out \(\displaystyle\pi\) and one (r), and we are left with:

\(\displaystyle P = \frac{2\sigma}{r} \)

The excess pressure (P) inside a spherical liquid drop is directly proportional to the surface tension (σ) and inversely proportional to the radius (r) of the drop. This means that smaller drops have higher excess pressure due to the tighter curvature of their surface.

Excess Pressure-flow Direction

Concave Meniscus: Excess pressure is directed inward, causing the liquid to rise. When we talk about a concave meniscus, we’re referring to the curved surface of a liquid that is higher at the edges and lower in the middle, like water in a glass tube.

Excess pressure is the additional pressure inside the liquid compared to the pressure outside. In a concave meniscus, this excess pressure is directed inward, towards the center of the curvature. To derive the expression for excess pressure, we’ll use the concept of surface tension and the geometry of the meniscus:

The force due to surface tension acts along the perimeter of the meniscus. If (σ) is the surface tension and (C) is the circumference, then the force is

\(\displaystyle F_{\text{surface tension}} = \sigma \times C \).

For a circular meniscus, \(\displaystyle C = 2\pi r \), where (r) is the radius of curvature of the meniscus. Substituting the circumference, we get

\(\displaystyle F_{\text{surface tension}} = \sigma \times 2\pi r \).

This force is applied over the cross-sectional area of the meniscus, which is a circle with radius (r). So, the area \(\displaystyle A = \pi r^2 \), and the force due to excess pressure is

\(\displaystyle F_{\text{excess pressure}} = P \times A \),

where (P) is the excess pressure. For equilibrium, the inward force due to surface tension must balance the outward force due to excess pressure:

\(\displaystyle \sigma \times 2\pi r = P \times \pi r^2 \)

Dividing both sides by \(\displaystyle \pi r^2 \), we find:

\(\displaystyle P = \frac{\sigma \times 2\pi r}{\pi r^2} \)

Simplifying, we cancel out \(\displaystyle \pi \) and one (r), giving us:

\(\displaystyle\begin{equation}\label{eqn:2}\boxed{\boldsymbol{ P = \frac{2\sigma}{r}}} \end{equation}\)

The excess pressure in a concave meniscus is directed inward because the surface tension pulls the liquid surface inwards, creating a pressure difference. This inward pressure is what causes the liquid to rise in the capillary tube.

Convex Meniscus: The excess pressure in a convex meniscus is the force that pushes the liquid down, and it’s determined by the surface tension and the size of the curvature. In a convex meniscus, the liquid surface curves downward, like a dome. This shape occurs when the cohesive forces between the liquid molecules are stronger than the adhesive forces between the liquid and the container.

Excess pressure is the additional pressure inside the liquid compared to the pressure outside. Excess pressure is directed outward, causing the liquid to be depressed. In a convex meniscus, this excess pressure is directed outward, away from the center of the curvature.

Since the meniscus is convex, the pressure inside the liquid is less than the atmospheric pressure, so we take the excess pressure as negative:

\(\displaystyle\begin{equation}\label{eqn:3}\boxed{\boldsymbol{P = -\frac{2\sigma}{r} }} \end{equation}\)

This result tells us that the excess pressure in a convex meniscus is inversely proportional to the radius of curvature (r) of the meniscus and directly proportional to the surface tension (σ), with a negative sign indicating the direction of the pressure.

Plane Meniscus: For a plane meniscus, there is no excess pressure due to surface tension because the surface is flat, and the forces are balanced. This means that the pressure within the liquid at the level of the meniscus is the same as the atmospheric pressure.

A plane meniscus occurs when the liquid surface is flat. This happens when the adhesive forces (attraction between the liquid and the container) and cohesive forces (attraction between the liquid molecules themselves) are equal. As a result, there is no net curvature and, therefore, no excess pressure due to surface tension.

In a plane meniscus, since there is no curvature, the concept of excess pressure due to surface tension doesn’t apply. The pressure throughout the liquid is uniform and equal to the atmospheric pressure (assuming the liquid is open to the atmosphere).

For a curved surface, the excess pressure (P) is given by the formula:

\(\displaystyle P = \frac{2\sigma}{r} \)

where (σ) is the surface tension and (r) is the radius of curvature.

However, in a plane meniscus, the radius of curvature (r) is infinite because the surface is flat. Plugging an infinite radius into the formula gives us:

\(\displaystyle\begin{equation}\label{eqn:4}\boxed{\boldsymbol{ P = \frac{2\sigma}{\infty} = 0}} \end{equation}\)

So, the excess pressure (P) in a plane meniscus is zero. This concept is important when considering the behavior of liquids in containers where the liquid does not wet the container walls, resulting in a flat surface. It’s a special case in the study of capillarity and fluid mechanics that illustrates the balance of forces in a fluid at rest.

Difference between Concave, Convex, and Plane Meniscus

Property	Concave Meniscus	Convex Meniscus	Weaker than the adhesive force
Shape	Curves upward, like a bowl	Curves downward, like a dome	Flat and level
Adhesive Force	Stronger than cohesive force	Weaker than cohesive force	Balanced with cohesive force
Cohesive Force	Weaker than adhesive force	Stronger than adhesive force	Balanced with adhesive force
Angle of Contact	Less than 90°	More than 90°	Exactly 90°
Surface Tension	Pulls liquid up the container walls	Pulls liquid towards the center	Evenly distributed across the surface
Liquid Behavior	Climbs up the container walls	Depressed in the center	Neither climbs nor depresses
Examples	Water in a glass tube	Mercury in a glass tube	Liquid in a tube with non-wetting liquid

This table summarizes the key differences in the behavior of liquids when they come into contact with solid surfaces, leading to different types of menisci.

Applications of Capillarity

Capillarity is a fascinating physical phenomenon that we can observe in many everyday situations. Here are some applications of capillarity.

• Plants and Trees: Capillarity helps transport water from the roots to the leaves in plants and trees. The narrow tubes inside the plants, called xylem vessels, use capillary action to draw water upwards against gravity.
• Paper Towels: When you spill water on the table and touch it with a corner of a paper towel, the liquid starts to spread through the towel. This is due to capillary action pulling the water into the tiny spaces between the fibers of the paper towel.
• Ink Pens: The ink in fountain pens and markers rises from the reservoir to the tip through narrow channels by capillary action, allowing you to write smoothly.
• Soil and Groundwater: Capillarity explains how groundwater moves through the soil’s pores, which is essential for agriculture. It also helps in designing efficient irrigation systems for crops.
• Medical Devices: In lab-on-a-chip devices, capillarity is used to move small amounts of fluids through microchannels for medical diagnostics and research.
• Paint Technology: Capillary action is crucial in paint technology, where it helps paint spread and adhere evenly over surfaces.
• Oil Lamps and Candles: The wick in an oil lamp or candle draws fuel upwards from the reservoir to the flame by capillary action, keeping the flame burning steadily.
• Blotting Paper: Blotting paper absorbs excess ink or oil due to the capillary action of the liquid being drawn into the spaces between the fibers of the paper.

These examples show how capillarity is not just a concept in textbooks but a vital part of many natural and human-made processes.

Solved Examples

Example 1: A capillary tube with an internal radius of 0.5 mm is dipped vertically in water. Calculate the height to which water will rise in the tube. Assume the surface tension of water is (0.072 N/m), the contact angle is (0^∘), and the density of water is (1000 kg/m³).

Solution: The height (h) of the capillary rise is given by:

\(\displaystyle h = \frac{2\sigma \cos \theta}{\rho g r} \)

• Surface tension, (σ = 0.072 N/m)
• Contact angle, (θ = 0^∘) (cos θ = 1))
• Density of water, (ρ = 1000 kg/m³)
• Radius of the capillary, (r = 0.5 mm = 0.0005 m)
• Acceleration due to gravity, (g = 9.8 m/s²)

Substituting the values:

\(\displaystyle h = \frac{2 \times 0.072 \times 1}{1000 \times 9.8 \times 0.0005} \)

\(\displaystyle h = \frac{0.144}{4.9} \)

\(\displaystyle h \approx 0.0294 \, \text{m} \)

So, the height to which water will rise in the capillary tube is approximately (0.0294 m) or (2.94 cm).

Example 2: A capillary tube with an internal radius of 0.2 mm is dipped in mercury. Calculate the height to which mercury will be depressed in the tube. Assume the surface tension of mercury is (0.465 N/m), the contact angle is (140^∘), and the density of mercury is (13500 kg/m³).

Solution: The height (h) of the capillary depression is given by:

\(\displaystyle h = \frac{2\sigma \cos \theta}{\rho g r} \)

• Surface tension, (σ = 0.465 N/m)
• Contact angle, (θ = 140^∘) (cos 140^∘ = -cos 40^∘ = -0.766)
• Density of mercury, (ρ = 13500 kg/m³)
• Radius of the capillary, (r = 0.2 mm= 0.0002 m)
• Acceleration due to gravity, (g = 9.8 m/s²)

Substituting the values:

\(\displaystyle h = \frac{2 \times 0.465 \times (-0.766)}{13500 \times 9.8 \times 0.0002} \)

\(\displaystyle h = \frac{-0.71214}{2.646} \)

\(\displaystyle h \approx -0.269 \, \text{m} \)

The negative sign indicates depression. So, the height to which mercury will be depressed in the capillary tube is approximately (0.269 m) or (26.9 cm).

Example 3: Compare the height of capillary rise for water and ethanol in the same capillary tube with a radius of 0.25 mm. The surface tension of water is (0.072 N/m) and for ethanol is (0.022 N/m). The densities are (1000 kg/m³) for water and (789 kg/m³) for ethanol. Assume the contact angle for both liquids is (0^∘).

Solution: The height (h) of the capillary rise is given by:

\(\displaystyle h = \frac{2\sigma \cos \theta}{\rho g r} \)

For water:

• (σ = 0.072 N/m)
• (ρ = 1000 kg/m³)
• (r = 0.25 mm = 0.00025 m)
• (cos θ = 1)

\(\displaystyle h_{\text{water}} = \frac{2 \times 0.072 \times 1}{1000 \times 9.8 \times 0.00025} \)

\(\displaystyle h_{\text{water}} = \frac{0.144}{2.45} \)

\(\displaystyle h_{\text{water}} \approx 0.0588 \, \text{m} \)

For Ethanol:

• (σ = 0.022 N/m)
• (ρ = 789 kg/m³)
• (r = 0.25 mm = 0.00025 m)
• (cos θ = 1)

\(\displaystyle h_{\text{ethanol}} = \frac{2 \times 0.022 \times 1}{789 \times 9.8 \times 0.00025} \)

\(\displaystyle h_{\text{ethanol}} = \frac{0.044}{1.936} \)

\(\displaystyle h_{\text{ethanol}} \approx 0.0227 \, \text{m}\)

So, the height of capillary rise for water is approximately (5.88 cm), and for ethanol, it is approximately (2.27 cm).

Example 4: If the radius of a capillary tube is halved, how does the height of the capillary rise change for water? Assume all other conditions remain the same.

Solution: The height (h) of capillary rise is inversely proportional to the radius (r) of the capillary tube:

\(\displaystyle h \propto \frac{1}{r} \)

If the radius is halved (\(\displaystyle r’ = \frac{r}{2} \)), the new height (h’) can be found by:

\(\displaystyle h’ = \frac{h}{\frac{r}{r’}} = \frac{h}{\frac{r}{r/2}} = 2h \)

Therefore, if the radius of the capillary tube is halved, the height of the capillary rise will double.

Example 5: A glass capillary tube and a plastic capillary tube, both with the same internal radius, are dipped in the same liquid. The contact angle for the liquid with glass is (30^∘) and with plastic is (90^∘). Compare the heights of capillary rise in both tubes.

Solution: The height (h) of the capillary rise is given by:

\(\displaystyle h = \frac{2\sigma \cos \theta}{\rho g r} \)

Given that the surface tension (σ), density (ρ), gravity (g), and radius (r) are the same for both tubes, the height of capillary rise depends on (cos θ).

For the glass tube (θ= 30^∘):

\(\displaystyle h_{\text{glass}} \propto \cos 30^\circ = \frac{\sqrt{3}}{2} \)

For the plastic tube (θ = 90^∘):

\(\displaystyle h_{\text{plastic}} \propto \cos 90^\circ = 0 \)

Therefore, the liquid will rise in the glass tube due to the non-zero cosine of the contact angle, while there will be no capillary rise in the plastic tube since (cos 90^∘ = 0).

FAQs