The story begins with the early astronomers who noticed the circular paths of stars and planets in the sky. They believed that celestial bodies moved in perfect circles, which was the accepted truth for many centuries.
The Greek philosopher Aristotle proposed that the Earth was stationary and everything in the heavens revolved around it in perfect circles. This geocentric model was widely accepted in the ancient world.
In the 16th century, Nicolaus Copernicus challenged the geocentric model, suggesting that the Earth and other planets orbit the Sun. His heliocentric model implied that circular motion was earthly and cosmic.
Johannes Kepler, using the meticulous observations of Tycho Brahe, discovered that planets move not in perfect circles but in ellipses. This was a significant shift from the idea of circular motion but still relied on the principles of rotation and revolution.
Sir Isaac Newton’s laws of motion and universal gravitation provided a mathematical framework for understanding circular motion. He showed that an object in motion would continue in a straight line unless acted upon by a force – in the case of circular motion, this force is centripetal, pulling the object towards the center of its path.
Today, circular motion principles are applied in various technologies and scientific endeavors, from satellites orbiting Earth to particles accelerated in colliders.
What Is Circular Motion
Circular motion is a type of motion in which an object moves along a circular path. In circular motion, the object’s velocity is constantly changing, not because its speed is changing, but because the direction of its velocity is changing.
One essential aspect of circular motion is centripetal acceleration, which is the acceleration directed toward the center of the circle along which the object is moving. This acceleration keeps the object moving in a circular path and is always perpendicular to the object’s velocity at any point along the path.
Centripetal force is the force that causes this acceleration. It acts towards the center of the circle and is responsible for keeping the object in its circular path. Centripetal force is necessary to counteract any tendency of the object to move in a straight line due to its inertia.
Angular Variables
Angular Displacement
Imagine you’re at the center of a merry-go-round, watching your friend on the edge. As the merry-go-round spins, your friend moves along a circular path. The angle between where your friend started and where they ended up after one full turn is what we call Angular Displacement.
In physics, when we talk about motion along a curved path, like a circle, we use angular displacement to describe the change in position. It’s similar to how we use regular displacement to talk about straight-line motion, but instead of meters, we measure angular displacement in degrees or radians.
Here’s a simple way to think about it:
- Angular Displacement (θ): It’s the angle formed by a line from the center of the circle to a point on its edge as it moves around. If your friend on the merry-go-round makes one full rotation, their angular displacement is 360 degrees or \(\displaystyle2\pi\) radians.
To calculate angular displacement, we use the formula:
\(\displaystyle\theta = \frac{s}{r}\)
- (θ) is the angular displacement in radians,
- (s) is the arc length, which is the distance your friend travels along the edge of the merry-go-round,
- (r) is the radius of the merry-go-round.
So, if your friend travels a distance equal to the circumference of the merry-go-round, their angular displacement is \(\displaystyle2\pi\) radians, because the circumference \(\displaystyle C = 2\pi r \), and plugging that into our formula gives us \(\displaystyle \theta = \frac{2\pi r}{r} = 2\pi \).
Angular displacement is a vector quantity, which means it has both magnitude (how much) and direction (which way). So if your friend goes clockwise, we consider it a positive displacement, and if they go counterclockwise, it’s negative.
Angular Velocity
Imagine a figure skater spinning on ice. The rate at which the skater turns around their axis is what we call angular velocity. It’s not about how far they move across the ice, but how fast they’re spinning in place.
Angular velocity is measured in terms of the angle covered per unit time. The standard unit is radians per second (rad/s). One radian is the angle made at the center of a circle by an arc whose length is equal to the radius of the circle.
The formula for angular velocity (ω) is:
\(\displaystyle\omega = \frac{\Delta \theta}{\Delta t}\)
where (∆θ) is the change in angular position (in radians), and (∆t ) is the change in time.
If our figure skater makes one full turn (360 degrees or \(\displaystyle 2\pi\) radians) in 2 seconds, their angular velocity would be:
\(\displaystyle\omega = \frac{2\pi \text{ radians}}{2 \text{ seconds}} = \pi \text{ radians/second}\)
The direction of angular velocity is given by the right-hand rule. If you curl the fingers of your right hand in the direction of rotation, your thumb points in the direction of the angular velocity vector.
Relation between Linear and Angular Speed
The linear speed (V) of a point on the edge of a rotating object is directly proportional to its distance from the center (r) and its angular speed (ω).
This is how fast an object rotates around a point. It’s like the speedometer of a car but for rotation, measuring how quickly the angle changes, typically in radians per second.
This is the speed at which a point on the rotating object moves through space. It’s the distance traveled per unit of time, like the speed of a runner on a track, measured in meters per second.
The link between linear and angular speed is beautifully simple. If you’re on a merry-go-round, your linear speed depends on how fast it’s spinning (angular speed) and how far you are from the center (radius). The formula that ties them together is:
\(\displaystyle V = r \times \omega \)
where (V) is linear speed, (r) is the radius of the circle, and (ω) is angular speed.
Imagine a record player. The angular speed is constant, but the linear speed of a point on the record changes depending on its distance from the center. Closer to the center, the linear speed is lower; near the edge, it’s higher, even though the angular speed is the same.
This relationship is crucial in designing gears, wheels, and engines. It helps us understand how the rotation of a motor translates into the forward motion of a car or the lift of a helicopter’s blades.
Angular Acceleration
Angular acceleration is the rate at which an object’s angular velocity changes. It’s like the accelerator pedal for rotation: press down, and you spin faster; let up, and you slow down.
Think of a spinning top. When you first twist it, it starts spinning slowly and then speeds up. That increase in spinning speed is due to angular acceleration.
We measure angular acceleration in radians per second squared (rad/s²). It tells us how quickly the angular velocity is changing every second. The formula is:
\(\displaystyle\alpha = \frac{\Delta \omega}{\Delta t}\)
where (α) is angular acceleration, (∆ω) is the change in angular velocity, and (∆t ) is the change in time.
If a fan takes 5 seconds to go from rest to spinning at 10 radians per second, its angular acceleration is:
\(\displaystyle\alpha = \frac{10 \text{ rad/s} – 0 \text{ rad/s}}{5 \text{ s}} = 2 \text{ rad/s}^2\)
The direction of angular acceleration depends on whether the object is speeding up or slowing down. If it’s speeding up in the counterclockwise direction, the angular acceleration is positive. If it’s slowing down or speeding up clockwise, it’s negative.
Equation of Circular Motion
The equation of circular motion describes the relationship between the various parameters involved in an object’s motion along a circular path. It typically includes quantities such as the object’s speed (v), the radius of the circular path (r), angular velocity (ω), and centripetal acceleration (ac).
One fundamental equation of circular motion is \(\displaystyle v = r \cdot \omega\), which relates the linear velocity (v) of the object to its angular velocity (ω) and the radius (r) of the circular path. Another important equation is \(\displaystyle a_c = \frac{v^2}{r}\), which represents the centripetal acceleration (ac) experienced by the object and is determined by its speed (v) and the radius (r) of the circular path.
Centripetal Force (Fc)
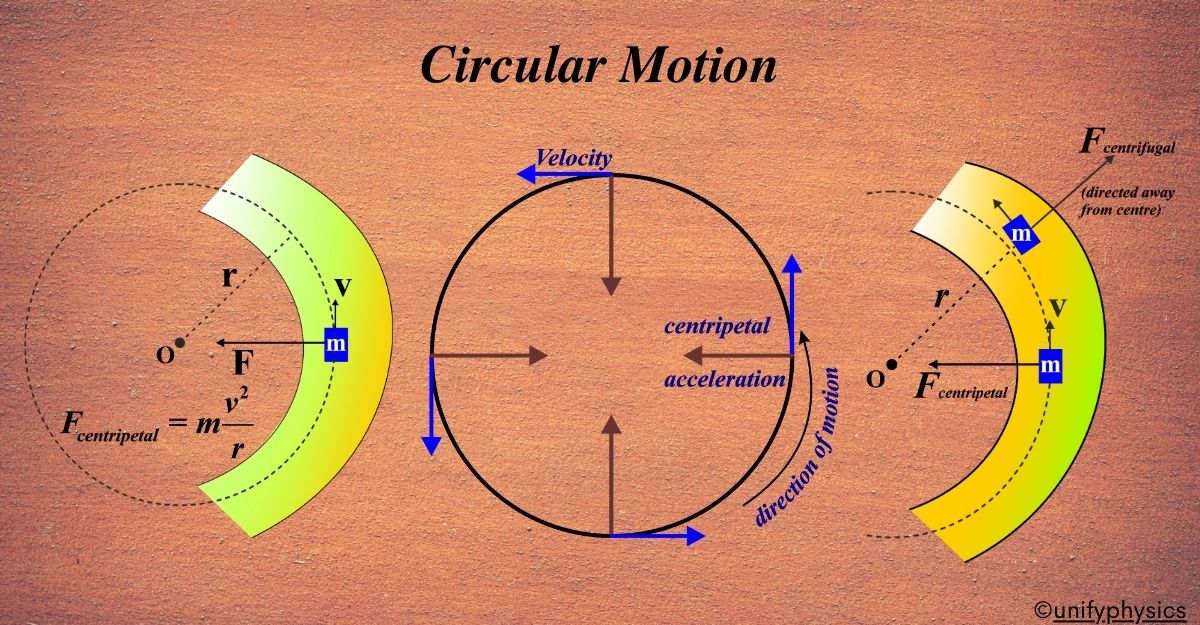
This is the force that keeps an object moving in a circle. It acts towards the center of the circle. Imagine an object circling a point. There’s no physical string attached, but it stays on its path as if pulled by an unseen force. This is the centripetal force at work.
The term ‘centripetal’ comes from Latin words meaning ‘center seeking’. True to its name, this force always points towards the center of the circle, pulling the object inward. Without this force, objects would move in a straight line due to inertia. Centripetal force is the reason they curve instead, constantly changing the direction of the object’s velocity.
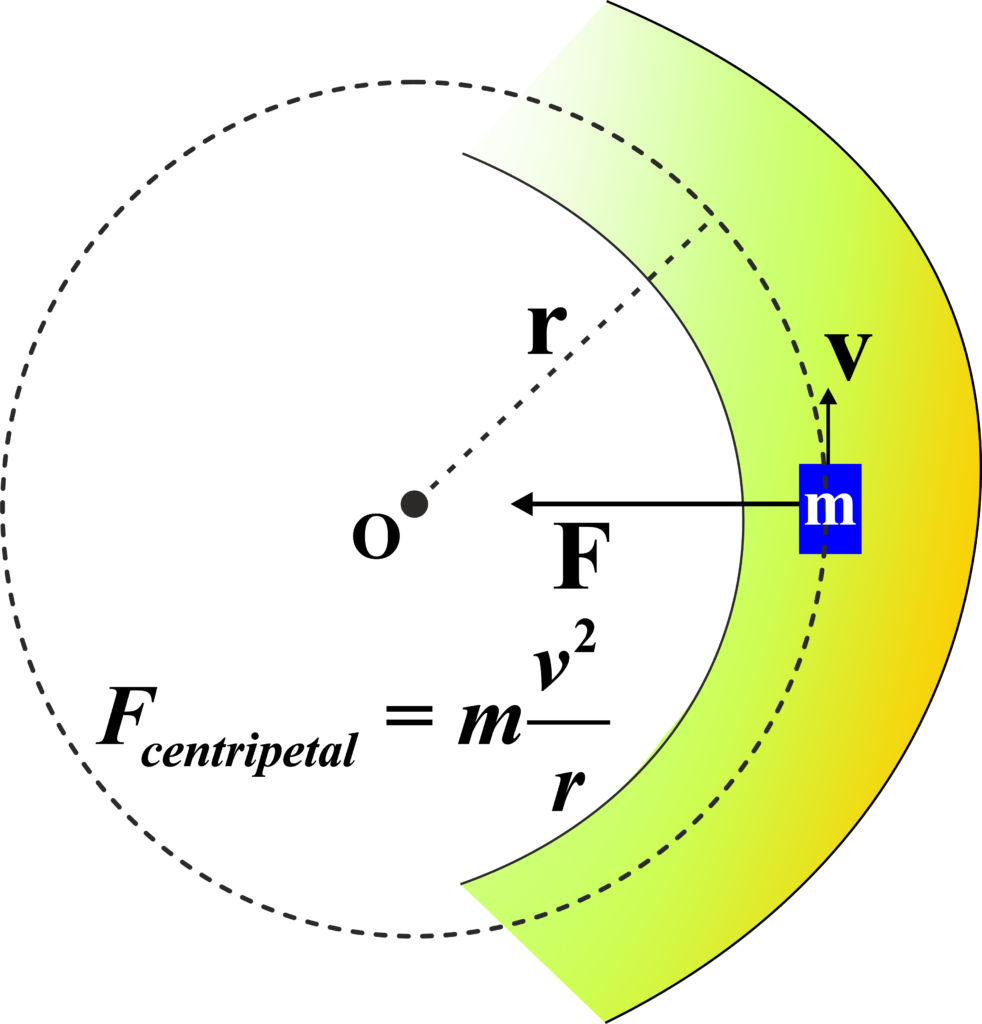
For an object to maintain a circular path, centripetal force must be constant, always acting perpendicular to the motion and towards the center of rotation. It’s important to note that centripetal force isn’t a new or special kind of force. It’s simply the name we give to the force that fulfills the role of keeping an object in circular motion, whether it’s tension, gravity, friction, or another force.
Centripetal force (Fc) is what keeps an object moving in a circle. It’s always directed towards the center of the circle. The formula for centripetal force is:
\(\displaystyle F_c = \frac{mV^2}{r} \)
Consider an object moving in a circle with a constant speed (V). The object’s velocity vector changes direction as it moves, which means there’s an acceleration. This acceleration, called centripetal acceleration (ac), is always pointed towards the center of the circle. By Newton’s second law, the force causing this acceleration is the centripetal force (Fc).
The centripetal acceleration is given by:
\(\displaystyle a_{c} = \frac{V^2}{r} \)
Applying Newton’s second law (F = ma), we get:
\(\displaystyle F_{c} = m \times a_{c} \)
Substituting the expression for (ac), we have:
\(\displaystyle F_{c} = m \times \frac{V^2}{r} \)
And there we have our formula for centripetal force. This is how fast the object rotates. It’s related to the linear speed (V) by the radius (r):
\(\displaystyle \omega = \frac{V}{r} \)
If we rearrange this equation to solve for (V), we get:
\(\displaystyle V = \omega \times r \)
Now, if we take the expression for (V) from the angular velocity and substitute it into the centripetal force equation, we get:
\(\displaystyle F_{c} = m \times \frac{(\omega \times r)^2}{r}\)
Simplifying, we find:
\(\displaystyle F_{c} = m \times \omega^2 \times r \)
Centrifugal Force (Fcf)
Centrifugal force is not a real force, it’s the apparent force that seems to push an object outward when it’s in a rotating frame of reference. It’s equal in magnitude but opposite in direction to the centripetal force.
Centrifugal force is often described as the “center-fleeing” force. It’s the sensation you feel when you’re taking a sharp turn in a car and you’re pushed against the door. Conceptually, it feels like a force is pulling you outward, away from the center of the circle.
The key to understanding centrifugal force is realizing that it’s a pseudo-force. It’s not a real force acting on you, but rather a result of your inertia — the tendency of an object to resist changes to its state of motion.
When you’re moving in a circle, your body wants to keep moving in a straight line (thanks to inertia).
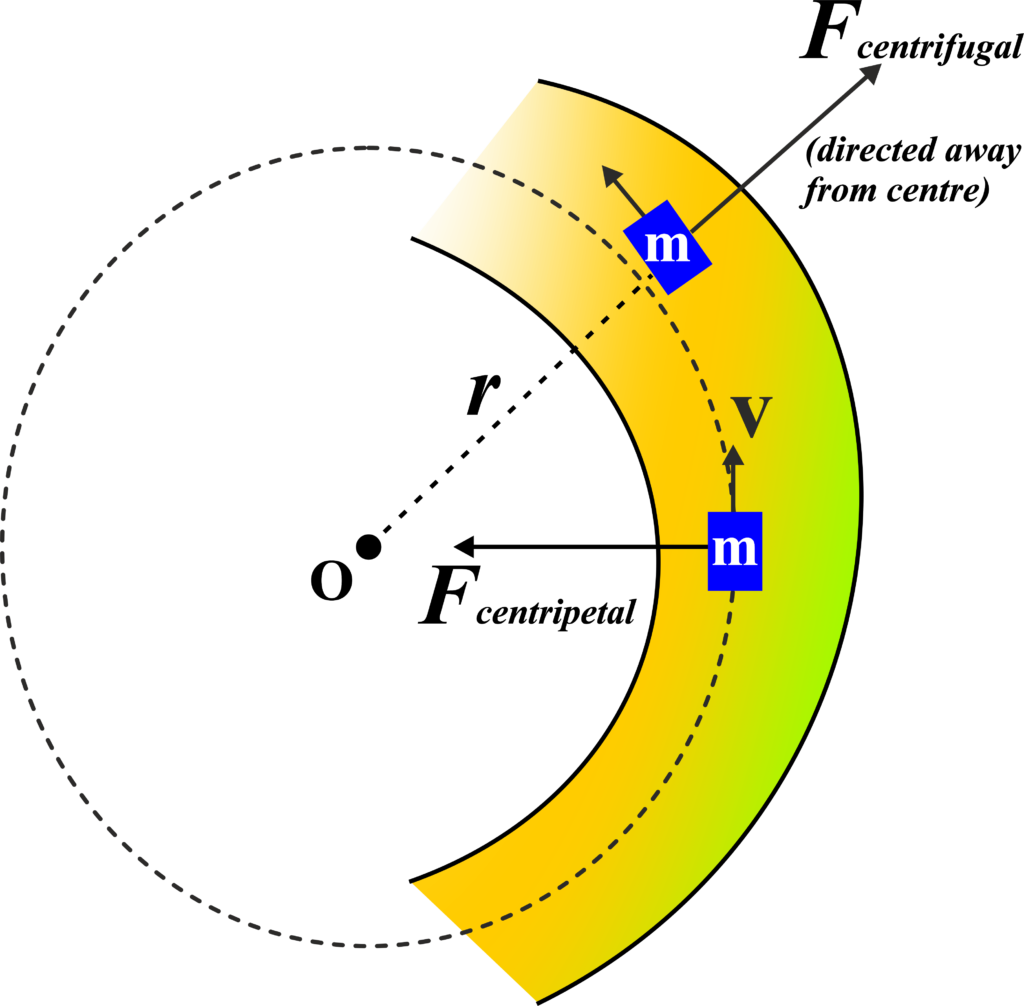
But the centripetal force keeps pulling you towards the center, changing your direction. Centrifugal force is what you ‘feel’ as your body resists this inward pull.
Centrifugal force only appears when you’re in a rotating reference frame. If you were to look at the situation from the outside, standing still, you wouldn’t see any outward force acting on the object. It’s purely a result of the rotating perspective.
In the equations of motion, you won’t find a term for centrifugal force. That’s because it’s not exerting a real influence on the object’s motion. It’s an artifact of the rotating frame, a phantom force that vanishes when viewed from a stationary point.
Angular Velocity (ω): This describes how fast an object rotates and is given by;
\(\displaystyle \omega = \frac{\Delta \theta}{\Delta t} \)
where (∆θ) is the change in angular position, and (∆t) is the change in time.
Tangential Velocity (Vt): This is the linear speed of an object moving along the circumference of the circle, related to angular velocity.
When we talk about objects moving in circles, there’s a special kind of speed called Tangential Velocity. It’s the linear speed, but for something that’s not going straight—it’s going around a curve.
It’s the speed at which a point on a rotating object is moving along its circular path. Imagine a point on the edge of a spinning wheel. As the wheel spins, this point moves around the circle. The speed at which it moves, measured along the edge of the circle, is its tangential velocity.
The word ‘tangential’ comes from ‘tangent’, which is a straight line that just touches a curve at one point without crossing it. So, tangential velocity is the speed of something moving along a path that’s always ‘touching’ the circle at just one point.
Angular velocity is all about how fast the angle is changing as something spins. Tangential velocity is different—it’s about how fast the object would be moving if you straightened out the circle into a line and let it go.
There’s a neat relationship between tangential velocity (Vt), angular velocity (ω), and the radius of the circle (r). It’s given by:
\(\displaystyle V_{t} = r \times \omega \)
This means the faster something spins (bigger (ω) or the further out you are from the center (bigger (r)), the greater your tangential velocity.
Tangential velocity helps us design everything from car tires to merry-go-rounds. It tells us how different parts of a rotating system are moving relative to each other, which is super important for making sure things don’t break apart or wear out too quickly. Tangential velocity is like the sprinter’s speed on the circular track of rotation, giving us a linear perspective on circular motion.
Angular Acceleration (α): When an object’s angular velocity changes, it experiences angular acceleration, calculated as:
\(\displaystyle \alpha = \frac{\Delta \omega}{\Delta t} \)
Kinematic Equations for Circular Motion: In linear motion, we have three kinematic equations that relate displacement (s), initial velocity (u), final velocity (v), acceleration (a), and time (t):
- First Equation: \(\displaystyle v = u + at\)
- Second Equation: \(\displaystyle s = ut + \frac{1}{2}at^2\)
- Third Equation: \(\displaystyle v^2 = u^2 + 2as\)
For circular motion, we replace linear displacement with angular displacement (θ), linear velocity with angular velocity (ω), and linear acceleration with angular acceleration (α).
Let’s start with the first equation for linear motion and adapt it for circular motion:
- Linear: \(\displaystyle v = u + at\)
- Circular: \(\displaystyle\omega = \omega_0 + \alpha t\)
where (ω0) is the initial angular velocity, (ω) is the final angular velocity, and (α) is the angular acceleration.
Now, let’s look at the second equation:
- Linear: \(\displaystyle s = ut + \frac{1}{2}at^2\)
- Circular: \(\displaystyle\theta = \omega_0 t + \frac{1}{2}\alpha t^2\)
where (θ) is the angular displacement.
Finally, the third equation:
- Linear: \(\displaystyle v^2 = u^2 + 2as\)
- Circular: \(\displaystyle\omega^2 = \omega_0^2 + 2\alpha \theta\)
Imagine a carousel starting from rest (ω0 = 0) and speeding up with a constant angular acceleration (α). After a time (t), we can use the first circular kinematic equation to find its angular velocity.
If we want to know how far a horse on the carousel has traveled in terms of angle, we use the second equation. To find the relationship between the angular velocities and the angular displacement without involving time, we use the third equation.
Also Read: Uniform Circular Motion
Type of Circular Motion
Circular motion can be uniform, with constant angular velocity, or non-uniform, where the speed changes due to angular acceleration. When studying motion, we come across different types of circular motion.
Uniform Circular Motion:
- This is the simplest of the two types. Here, an object moves along a circular path at a constant speed. Think of a car going around a racetrack at a steady pace, not speeding up or slowing down.
- Despite the speed being constant, the velocity is not. Since velocity is a vector quantity (meaning it has both magnitude and direction), and the direction is continually changing as the object moves around the circle, the object is accelerating. This acceleration is called centripetal acceleration and is always directed towards the center of the circle.
Non-Uniform Circular Motion:
- In this type, the object’s speed changes as it moves along the circular path. This could be a car on a racetrack that speeds up on the straights and slows down on the curves.
- The changing speed means there’s an additional component of acceleration at play here, called tangential acceleration, which is along the direction of motion. This is in addition to the centripetal acceleration that changes the direction of the velocity.
Both planetary and rotational motion are types of circular motion, but they occur on different scales and involve different forces. Planetary motion is the grand scale of celestial bodies orbiting due to gravity, while rotational motion is the more localized spin of an object around its axis.
Planetary Motion:
- Kepler’s Laws: The motion of planets around the sun is governed by Kepler’s laws. These laws describe the elliptical orbits of planets, with the sun at one focus, and explain how planets sweep out equal areas in equal times during their orbit, indicating that they move faster when closer to the sun⁵⁶.
- Gravitation: Planetary motion is a delicate dance guided by gravity. The gravitational pull between the sun and a planet dictates the shape and speed of the planet’s orbit, creating a cosmic rhythm that has persisted for eons.
Rotational Motion:
- Rigid Body Rotation: Rotational motion involves an object spinning around a fixed axis. It’s like a top spinning on a table; every part of the top moves in a circle around the axis of rotation. This type of motion is characteristic of rigid bodies — objects that don’t deform as they spin.
- Dynamics of Rotation: The dynamics of rotational motion are analogous to linear motion but with a twist. Instead of forces, we talk about torques; instead of mass, we discuss the moment of inertia. These concepts help us understand how objects resist changes in their rotational state and how they’re influenced by applied forces.
Application
Applications of Centripetal Force: This force is at play in amusement park rides, the orbits of planets, and the turns of a racecar.
- In the vast expanse of space, centripetal force is the glue that holds our solar system together. The planets orbit the sun because of the gravitational pull acting as a centripetal force, keeping them in their elliptical paths.
- When engineers design roads and vehicles, they account for centripetal force. Curved roads are banked to provide the necessary centripetal force to prevent vehicles from skidding out of their lanes.
- Ever wondered why you don’t fly out of your seat on a roller coaster loop? It’s the centripetal force! The tracks are designed to exert this force, keeping the cars and their thrilled passengers safely in motion.
- In sports like hammer throw and discus, athletes rely on centripetal force to keep the object in a circular path before releasing it to achieve maximum distance.
- Satellites orbiting Earth must maintain a circular path, and it’s the centripetal force due to Earth’s gravity that keeps them from shooting off into space. This stable orbit is crucial for global communication networks.
Experiences of Centrifugal Force: Centrifugal Force is often misunderstood because it’s not a force in the traditional sense. It’s a pseudo force that appears to act on objects when they are in a rotating reference frame. Let’s explore its applications
- Scientists use centrifuges to separate substances of different densities. The rapid spinning creates a strong ‘centrifugal force’ that causes denser particles to move outward, separating them from lighter ones.
- Rides like the “Rotor” and “Gravitron” use the concept of ‘centrifugal force’ to pin riders against the wall as the ride spins. Riders feel as if an outward force is holding them in place, but it’s their inertia.
- When a vehicle takes a sharp turn, passengers feel pushed to the side opposite the turn. This sensation, attributed to ‘centrifugal force’, is their inertia resisting the change in direction. Understanding this helps improve vehicle stability in turn.
- Satellites in geosynchronous orbit appear to experience ‘centrifugal force’ that counteracts the pull of gravity, keeping them in a stable orbit. This balance allows satellites to remain over a fixed point on Earth’s surface.
Solved Examples
Example 1: A car is moving along a circular track of a radius of 100 meters with a constant speed of 20 m/s. Calculate the magnitude and direction of the acceleration of the car.
Solution: Given: The radius of the track, (r = 100) m ; Speed of the car, (v = 20) m/s
The magnitude of acceleration in uniform circular motion is given by:
\(\displaystyle a = \frac{v^2}{r} \)
Substituting the given values:
\(\displaystyle a = \frac{(20 \, \text{m/s})^2}{100 \, \text{m}} = 4 \, \text{m/s}^2 \)
The direction of acceleration in uniform circular motion is towards the center of the circle, which is radial inward.
Example 2: A small mass of 0.1 kg is tied to a string and whirled in a horizontal circle of radius 2 meters at a constant speed of 5 m/s. Calculate the tension in the string.
Solution: Given: Mass of the object, (m = 0.1) kg; The radius of the circle, (r = 2) m; Speed of the object, (v = 5) m/s
The tension in the string provides the necessary centripetal force, given by:
\(\displaystyle T = \frac{mv^2}{r} \)
Substituting the given values:
\(\displaystyle T = \frac{(0.1 \, \text{kg}) \times (5 \, \text{m/s})^2}{2 \, \text{m}} = 12.5 \, \text{N} \)
Example 3: A cyclist is riding along a circular track of a radius of 50 meters at a constant speed of 10 m/s. Calculate the period and frequency of the motion.
Solution: Given: The radius of the track, (r = 50) m: Speed of the cyclist, (v = 10) m/s
The period of motion in uniform circular motion is given by:
\(\displaystyle T = \frac{2\pi r}{v} \)
Substituting the given values:
\(\displaystyle T = \frac{2 \times \pi \times 50 \, \text{m}}{10 \, \text{m/s}} = 10 \pi \, \text{s} \)
The frequency is the reciprocal of the period:
\(\displaystyle f = \frac{1}{T} = \frac{1}{10\pi} \approx 0.0318 \, \text{Hz} \)
Example 4: A satellite is orbiting Earth in a circular orbit with a radius of (6.4× 106) meters. Calculate its orbital speed given that the acceleration due to gravity is ( 9.8 ) m/s².
Solution: Given: Radius of the orbit, \(\displaystyle r = 6.4 \times 10^6\) m: Acceleration due to gravity, (g = 9.8) m/s²
The orbital speed of the satellite is given by:
\(\displaystyle v = \sqrt{\frac{G M}{r}} \)
Where (G) is the gravitational constant and (M) is the mass of Earth.
\(\displaystyle v = \sqrt{\frac{(6.67 \times 10^{-11} \, \text{Nm}^2/\text{kg}^2) \times (5.97 \times 10^{24} \, \text{kg})}{6.4 \times 10^6 \, \text{m}}} \approx 7691 \, \text{m/s} \)
Example 5: A car enters a curve with a radius of 50 meters at a speed of 20 m/s. If the coefficient of static friction between the tires and the road is 0.6, will the car be able to navigate the curve without skidding?
Solution: Given: The radius of the curve, (r = 50) m; Speed of the car, (v = 20) m/s; Coefficient of static friction, (μ= 0.6 )
The maximum speed of the car without skidding is given by:
\(\displaystyle v_{\text{max}} = \sqrt{\mu g r} \)
Substituting the given values:
\(\displaystyle v_{\text{max}} = \sqrt{(0.6)(9.8 \, \text{m/s}^2)(50 \, \text{m})} \approx 17.32 \, \text{m/s} \)
Since (\(\displaystyle v < v_{\text{max}} \)), the car can navigate the curve without skidding.
FAQs
What is the difference between linear and circular motion?
Linear motion occurs when an object moves in a straight line, while circular motion occurs when an object moves along a circular path. In linear motion, velocity and acceleration may change in magnitude or direction, while in circular motion, the velocity changes direction continuously, resulting in centripetal acceleration.
How does centripetal force keep an object in circular motion?
Centripetal force is the force directed toward the center of a circular path that keeps an object in circular motion. It is necessary to counteract the tendency of an object to move in a straight line due to inertia. Without centripetal force, the object would continue in a straight line tangent to the circle.
Can you explain the concept of centripetal acceleration in circular motion?
Centripetal acceleration is the acceleration directed towards the center of a circular path. It results from a change in the direction of the velocity vector, even if the magnitude of the velocity remains constant. Centripetal acceleration allows an object to continuously change direction while moving in a circle.
How does angular velocity differ from linear velocity in circular motion?
Angular velocity measures the rate of rotation or angular displacement of an object around a central point, typically in radians per unit of time. Linear velocity, on the other hand, measures the rate of change of position of an object along its path in a straight line. While angular velocity relates to rotational motion, linear velocity relates to straight-line motion.
What role does friction play in circular motion?
Friction can provide the centripetal force required for circular motion when an object moves in a horizontal circle on a surface. For example, when a car makes a turn, the friction between the tires and the road provides the centripetal force necessary to keep the car moving along the curved path.
Can an object experience uniform circular motion without a net force acting on it?
No, an object cannot experience uniform circular motion without a net force acting on it. According to Newton’s first law of motion, an object in motion will continue moving in a straight line at a constant velocity unless acted upon by a net force. In circular motion, the continuously changing direction of the velocity vector requires a net force, known as centripetal force.
How does the concept of centrifugal force relate to circular motion?
Centrifugal force is often mistakenly thought of as a real force acting outward on an object in circular motion. However, centrifugal force is a fictitious or pseudo-force experienced by an observer in a rotating reference frame, and it appears to push objects away from the center of rotation. In reality, it is the inertia of the object trying to move in a straight line tangent to the circle.