Coherent And Incoherent Addition of Waves

The journey into understanding coherent and incoherent waves begins with the fundamental nature of light and its wave-like behavior. Historically, the debate over whether light was composed of particles or waves was a significant one, with notable figures like Isaac Newton advocating for the particle theory. However, it was the wave theory of light that eventually paved the way for the concepts of coherence and incoherence.

The wave theory gained traction through the work of Christiaan Huygens in the 17th century, who proposed that light was a wave phenomenon. This theory was further supported by Thomas Young’s double-slit experiment in the early 19th century, which demonstrated the interference of light waves and suggested that light could exhibit wave-like properties.

The term “coherence” was introduced to describe the ability of waves to display well-defined phase relationships. Coherent waves, as we understand them today, are those that maintain a constant phase difference, allowing for predictable interference patterns. The development of lasers in the 20th century provided a practical and powerful source of coherent light, which has been instrumental in advancing our understanding of wave optics.

In contrast, incoherent waves were recognized as those with random phase relationships. This was observed in natural light sources, such as the sun, where the multitude of atomic and molecular processes resulted in light waves with varying phases and frequencies. The study of incoherent light has been crucial in fields like thermal radiation and blackbody radiation.

The 20th century also saw the rise of quantum mechanics, which brought a new perspective to the nature of waves and their coherence. Quantum theory describes particles as having wave-like properties, and this duality has been essential in explaining the behavior of both coherent and incoherent waves at the microscopic level.

What are Coherent Sources?

Coherent sources are two or more waves that emit waves with a constant phase difference and the same frequency. Examples include lasers and certain radio wave transmitters.

Imagine you’re at a concert where two guitars are playing the same note perfectly in sync. The sound waves from these guitars are like coherent sources in physics. In the world of waves, especially light waves, coherent sources are akin to these guitars, but instead of music, they emit light waves in harmony.

A coherent source produces waves consistently marching in step with each other. These waves have:

• The same frequency: Like two singers hitting the same note, coherent waves vibrate at the same rate.
• A constant phase relationship: This means the peaks and valleys of the waves from coherent sources align in a regular, repeating pattern, much like soldiers marching in a parade.

Coherent sources are special because they allow us to observe fascinating phenomena like interference patterns, where waves can add up to make brighter lights or cancel each other out to create darkness. They’re the secret behind the magic of holograms and the precision of scientific instruments.

Characteristics of Coherent Sources:

When we talk about coherent sources in physics, we’re referring to sources that produce waves that are in lockstep. Here are the key features that define coherent sources:

• Constant Phase Difference: Imagine two friends on swings who are swinging in perfect unison. This synchronization is similar to coherent waves, which maintain the same phase relationship over time, meaning their peaks and troughs match up consistently.
• Single Frequency: Coherent sources are like singers hitting the same note continuously. They emit waves that oscillate at the same rate, which means they have the same frequency.
• Same Amplitude: The waves from coherent sources have the same strength or loudness, known as amplitude. This uniformity is crucial for creating stable and predictable interference patterns.

These characteristics allow coherent sources to produce a stable interference pattern, where the positions of the bright and dark bands (maxima and minima) don’t shift around. This stability makes coherent sources so useful in experiments and applications like holography and fiber optics communication.

What are Incoherent Sources?

Incoherent sources emit waves that have random phase differences and may have different frequencies. Common examples are light bulbs and the sun. To understand incoherent sources, let’s think of a bustling city street. Just as the sounds from cars, people, and the environment blend into a cacophony without any rhythm or pattern, incoherent sources emit mixed waves, with no regular synchronization. Incoherent sources are like the sun or a light bulb in your room. They send out waves that:

The waves from these sources are like conversations in a crowded room, where each word from different people starts and stops at random times. Each wave can have a different pitch, like musical instruments playing tunes. Light is produced when atoms release energy spontaneously, without any set order or timing. The most common incoherent sources are tungsten filament lamps and fluorescent tubes.

Characteristics of Incoherent Sources:

When we talk about incoherent sources in the context of physics, we’re referring to sources that emit waves with no fixed relationship between them. Here’s a simple breakdown of their characteristics:

• Random Phase Relationship: Unlike coherent sources, incoherent sources produce waves where the peaks and troughs don’t align in a consistent pattern. It’s like a group of dancers all moving to different beats.
• Varying Frequencies: Incoherent sources emit waves that can have a variety of frequencies. Imagine a choir where each member is singing a different note; that’s how incoherent sources operate, with each wave at its unique frequency.
• Independent Emission: The waves from incoherent sources are emitted independently of one another. Each atom or molecule releases energy randomly, without any synchronization with others.

These characteristics mean that incoherent sources don’t produce a stable interference pattern. Instead, the waves mix in a complex way, much like the overlapping conversations in a busy marketplace.

Superposition Principle

The superposition principle states that when two or more waves overlap, the resulting wave displacement is the sum of the individual wave displacements at each point. Imagine you’re at the beach, watching waves come ashore. If two waves meet, they don’t just crash into each other and stop; they combine. The height of the water where they meet is the sum of the heights of the individual waves. If both waves are 1 meter high, the combined wave is 2 meters high at the point where they meet. This is the essence of the superposition principle.

In physics, when two or more waves overlap, the resulting wave at any point is the sum of the displacements of the individual waves at that point. If one wave has a displacement of (A) and another has a displacement of (B), the resulting wave’s displacement at the point where they meet is ( A + B ).

The superposition principle can lead to two types of interference:

• Constructive Interference: When the wave crests (high points) and troughs (low points) align, they add up to make a bigger wave.
• Destructive Interference: When the crest of one wave meets the trough of another, they cancel each other out, leading to a smaller wave or no wave at all.

Mathematically, if two waves are described by functions f(x) and g(x), the superposition principle tells us that the resulting wave is described by the function f(x) + g(x).

Constructive Interference:

When waves from coherent sources meet in phase, their amplitudes add up, resulting in a wave with greater amplitude. This is known as constructive interference. Constructive interference occurs when two waves meet and combine to form a wave with a larger amplitude. It’s like when two ripples in a pond collide and create a bigger wave.

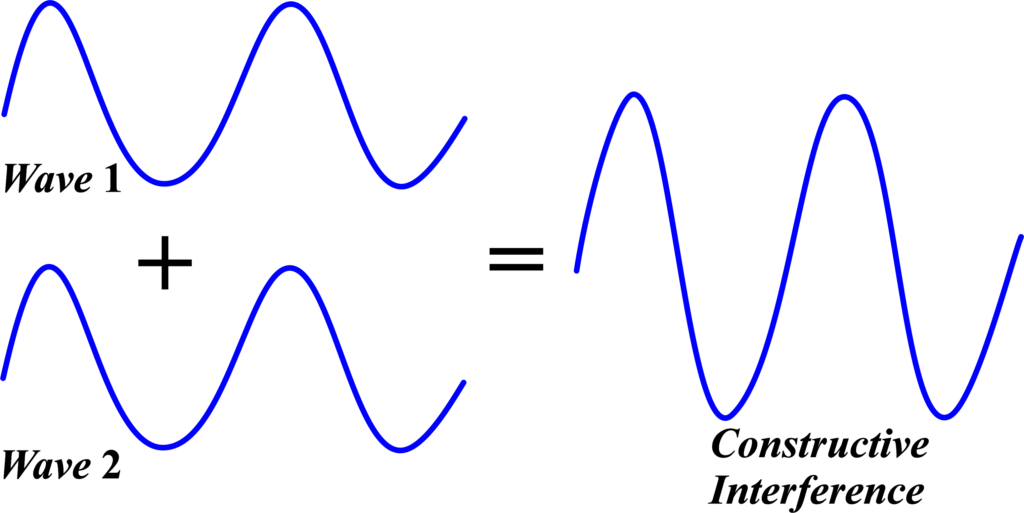
This phenomenon happens when the crests (the highest points) of two waves align with each other. The waves “add up” to make a new wave that’s bigger than either of the original waves. It’s similar to two people pushing a swing in the same direction at the same time; the swing goes higher.

Mathematically, if we have two waves with amplitudes (A₁) and (A₂), and they are in phase (meaning their peaks and troughs line up), the amplitude of the resulting wave (A) is the sum of the two:

\(\displaystyle A = A_1 + A_2 \)

If you could see constructive interference in action, you’d notice that at the points where the waves meet, the medium (like water or air) moves higher (if the waves are upward) or lower (if the waves are downward) than the individual waves. The result of constructive interference is a wave that is stronger and carries more energy than the individual waves. This is why, in some situations, sounds can suddenly seem louder or lights can appear brighter.

Destructive Interference:

Destructive interference occurs when waves from coherent sources meet out of phase, causing their amplitudes to subtract from each other, potentially resulting in complete cancellation. Imagine two identical waves traveling towards each other. Destructive interference happens when the crest of one wave meets the trough of another, and they cancel each other out. It’s like two equal but opposite forces pulling on an object, resulting in no movement.

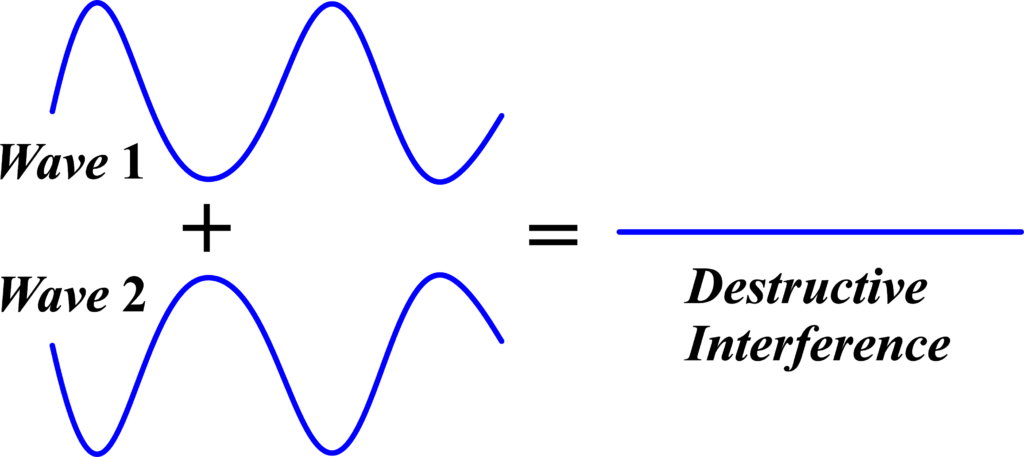
When destructive interference occurs, the amplitude of the resulting wave is less than the original waves. In some cases, they can cancel each other out completely, resulting in no wave at all.

For destructive interference to happen, two conditions must be met:

• The waves must have the same amplitude but in opposite directions.
• The phase difference between the waves should be an odd multiple of π, which means they are half a wavelength out of sync.

If two waves with amplitudes (A) are out of phase by (\(\displaystyle \pi \)) (180 degrees), the resulting amplitude (R) is:

\(\displaystyle R = A – A = 0 \)

If you could see destructive interference in action, you’d notice that at the points where the waves meet, the medium (like water or air) doesn’t move up or down—it stays flat because the waves have canceled each other out.

Locus of Point:

The locus of a point refers to the set of points where waves from coherent sources consistently interfere constructively or destructively. The word “locus” is Latin for “place” or “location”. In physics and mathematics, it refers to the set of points that satisfy a particular condition or rule.

In the realm of waves, the locus of a point is the path that a point follows as it moves according to a specific rule. For instance, if we’re talking about light waves emanating from a source, the locus would be the path or area where the light reaches.

Think of a flashlight shining on a wall. The spot of light on the wall is a point on the locus of the light beam. As you move the flashlight, the spot moves, tracing a path on the wall. This path is the locus of points where the light can reach.

Understanding the locus of a point helps us predict where waves will go and how they will behave. It’s a concept crucial for designing optical instruments and understanding the behavior of light in different mediums.

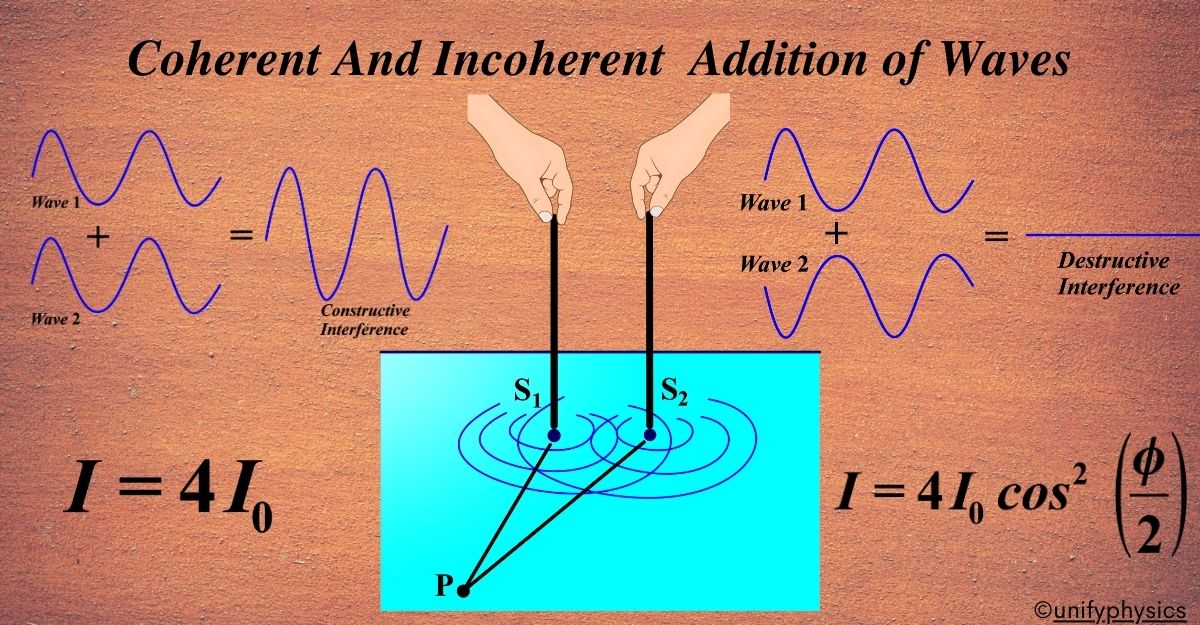
Derivation of Coherent and Incoherent Addition of Two Waves

Coherent Addition of Two Waves:

Imagine two needles, (S₁) and (S₂), moving up and down on the surface of water, creating ripples that travel towards a point (P). The path difference between the ripples reaching a point (P) from (S₁) and (S₂) is given by (S₁P – S₂P).

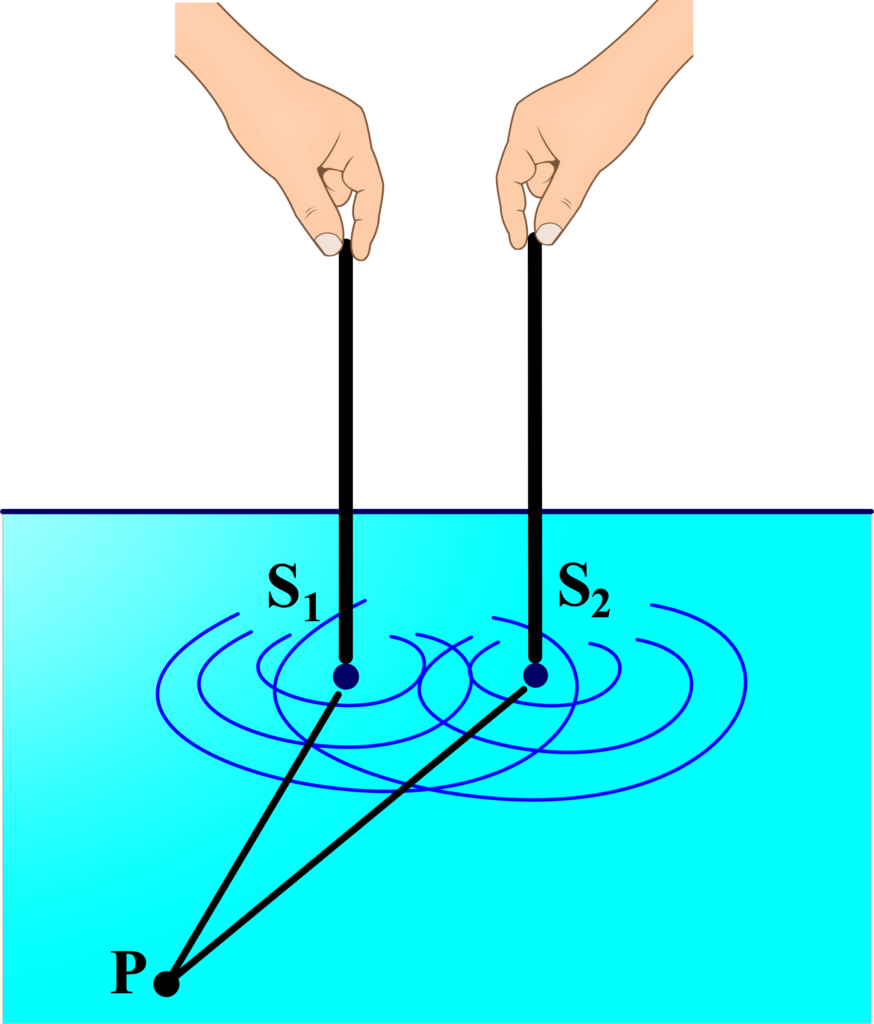
The displacement caused by the needles at any time (t) can be represented as:

\(\displaystyle y_1 = A\cos(\omega t) \)
\(\displaystyle y_2 = A\cos(\omega t) \)$

Here, (A) is the amplitude of the waves, and (\(\displaystyle \omega \)) is the angular frequency.

The resultant displacement (y) at point (P) due to the superposition of (y₁) and (y₂) is:

\(\displaystyle y = y_1 + y_2 \)

Substituting the values of (y₁) and (y₂), we get:

\(\displaystyle y = A\cos(\omega t) + A\cos(\omega t) \)
\(\displaystyle y = 2A\cos(\omega t) \)

Since the intensity (I) is proportional to the square of the amplitude of the waves, we have:

\(\displaystyle I_0 \propto A^2 \)

For our coherent waves, the intensity of the resultant wave (I) would be:

\(\displaystyle I \propto (2A)^2 \)
\(\displaystyle I = 4I_0 \)

This shows that the intensity of the resultant wave is four times the intensity of one of the individual waves.

Incoherent Addition of Two Waves:

For incoherent waves, the phase relationship between the waves is random, and the path difference (S₁P – S₂P) changes over time. This means we cannot simply add the amplitudes as we did for coherent waves.

Instead, we consider the average intensity over time. Since the waves are incoherent, the average resultant intensity (I) is the sum of the individual intensities of the waves:

\(\displaystyle I = I_1 + I_2 \)

If (I₀) is the intensity of one wave, then for two incoherent waves with the same intensity, the total intensity is:

\(\displaystyle I = I_0 + I_0 \)
\(\displaystyle I = 2I_0 \)

To find the intensity of the resultant wave from the given conditions, we’ll use the derived expression for the displacement (y) and then relate it to the intensity, which is proportional to the square of the amplitude.

Given the displacement of the two waves as:

\(\displaystyle y_1 = a\cos(\omega t) \)
\(\displaystyle y_2 = a\cos(\omega t + \varphi) \)

The resultant displacement (y) when they superpose is:

\(\displaystyle y = y_1 + y_2 \)
\(\displaystyle y = a\left[ \cos(\omega t) + \cos(\omega t + \varphi) \right] \)

Using the trigonometric identity for the sum of cosines:

\(\displaystyle y = 2a\cos\left( \frac{\varphi}{2} \right)\cos\left( \omega t + \frac{\varphi}{2} \right) \)

The amplitude of the resultant wave (A) is the coefficient of the cosine term, which is:

\(\displaystyle A = 2a\cos\left( \frac{\varphi}{2} \right) \)

Now, since the intensity (I) is proportional to the square of the amplitude, we have:

\(\displaystyle I \propto A^2 \)

Substituting the expression for (A) into the intensity formula, we get:

\(\displaystyle I \propto \left( 2a\cos\left( \frac{\varphi}{2} \right) \right)^2 \)
\(\displaystyle I = k \left( 2a\cos\left( \frac{\varphi}{2} \right) \right)^2 \)

Where (k) is a constant of proportionality. If (I₀) is the intensity of one of the individual waves with amplitude (a), and since (\(\displaystyle I_0 \propto a^2 \)), we can write:

\(\displaystyle I = 4I_0\cos^2\left( \frac{\varphi}{2} \right) \)

This is the intensity of the resultant wave for two coherent sources with a phase difference (\(\displaystyle \varphi \)) and the same amplitude (a). The intensity varies with the cosine squared of half the phase difference, showing how the phase difference affects the intensity due to constructive and destructive interference.

When coherent waves (such as those from a laser) combine, they maintain a fixed phase relationship. This means their crests and troughs align consistently. Constructive interference occurs when the waves are in phase (crests align), resulting in bright regions (maxima) in the interference pattern. Destructive interference happens when the waves are out of phase (crest meets trough), leading to dark regions (minima) in the pattern. Coherent interference produces clear and sharp fringes in experiments like the double-slit setup. Coherent sources are essential for applications like holography, fiber optics, and precision measurements.

Incoherent sources (like sunlight or light bulbs) emit waves with random phases. These waves don’t maintain a fixed relationship. When incoherent waves combine, their interference patterns are less distinct. The superposition of waves with varying phases leads to partial cancellation. The fringes are less pronounced, and the overall contrast between maxima and minima is reduced. Incoherent interference is still possible (e.g., with sunlight), but the fringes are harder to observe due to the randomness of phase differences. Incoherent sources are common in everyday lighting but can still exhibit interference effects under specific conditions.

Remember that no light source is entirely coherent or incoherent; most light falls somewhere in between. The ability to form interference fringes depends on the degree of coherence, which varies based on the source’s spectral properties and phase relationships.

Also Read: Huygens Principle

Sample Questions

Example 1: Using the superposition principle, explain how the resultant displacement is calculated when two waves overlap.

Solution: The superposition principle states that when two or more waves overlap, the resultant displacement at any point is the algebraic sum of the displacements due to each wave at that point.

Consider two waves (y₁) and (y₂) represented by:

\(\displaystyle y_1 = A \sin (kx – \omega t)\)
\(\displaystyle y_2 = A \sin (kx – \omega t + \phi)\)

Where (Φ) is the phase difference between the waves. Using the superposition principle, the resultant displacement ( y ) is:

\(\displaystyle y = y_1 + y_2\)
\(\displaystyle y = A \sin (kx – \omega t) + A \sin (kx – \omega t + \phi)\)

Using the trigonometric identity:

\(\displaystyle\sin a + \sin b = 2 \sin \left(\frac{a+b}{2}\right) \cos \left(\frac{a-b}{2}\right)\)

We get:

\(\displaystyle y = 2A \cos \left(\frac{\phi}{2}\right) \sin \left(kx – \omega t + \frac{\phi}{2}\right)\)

Using the superposition principle, the resultant displacement of overlapping waves is the sum of their displacements. For two waves with a phase difference, the resultant wave can be found using trigonometric identities.

Example 2: Determine the conditions for constructive and destructive interference.

Solution: Constructive Interference

• Occurs when the path difference between the two waves is an integral multiple of the wavelength.
• Condition: ( \(\displaystyle\Delta \phi = 2n\pi \)) or (\(\displaystyle \Delta x = n\lambda\) )

Destructive Interference:

• Occurs when the path difference between the two waves is an odd multiple of half the wavelength.
• Condition: (\(\displaystyle \Delta \phi = (2n+1)\pi \)) or ( \(\displaystyle\Delta x = (n + \frac{1}{2})\lambda \))

Consider two waves with the same amplitude and wavelength meeting at a point. If the path difference is ( \(\displaystyle\Delta x = \lambda\) ):

• For constructive interference: ( \(\displaystyle\Delta x = \lambda\) )
• For destructive interference: ( \(\displaystyle\Delta x = \frac{\lambda}{2}\) )

Constructive interference occurs when the path difference is an integer multiple of the wavelength (nλ). Destructive interference occurs when the path difference is an odd multiple of half the wavelength (\(\displaystyle n + \frac{1}{2})\lambda\)).

Example 3: Determine the locus of points where constructive interference occurs for two coherent point sources separated by a distance (d) and emitting waves of wavelength (λ).

Solution: Constructive interference occurs at points where the path difference between the waves from the two sources is an integer multiple of the wavelength:

\(\displaystyle\Delta x = n\lambda\)

For two point sources (S₁) and (S₂), the path difference at any point (P) on the plane is:

\(\displaystyle |S_1P – S_2P| = n\lambda\)

Locus of Points: The locus of points where constructive interference occurs is a set of hyperbolas with the two-point sources as foci.

For a given (n), the equation of the hyperbola is:

\(\displaystyle |S_1P – S_2P| = n\lambda\)

The locus of points where constructive interference occurs for two coherent point sources is a set of hyperbolas centered on the line joining the two sources, with the sources as foci.

FAQs