The study of collisions dates back to the times when early philosophers and scientists began to understand the nature of motion and forces. However, the most significant advancements came with the work of Sir Isaac Newton in the 17th century. His formulation of the three laws of motion laid the foundation for classical mechanics, including the principles governing collisions.
Newton’s third law of motion is particularly relevant to collisions. It states that for every action, there is an equal and opposite reaction. This means that when two objects collide, they exert forces on each other that are equal in magnitude and opposite in direction.
In the 18th and 19th centuries, scientists like Daniel Bernoulli and John Stuart Mill further developed the understanding of kinetic theory and the conservation of energy, which are crucial to analyzing collisions. They recognized that not all collisions are the same, and the outcomes depend on the properties of the colliding bodies and the forces involved.
The 20th century brought a deeper understanding of atomic and subatomic particles, leading to the development of quantum mechanics. Scientists like Niels Bohr and Werner Heisenberg studied collisions at the atomic level, which obey different rules than macroscopic objects due to the principles of quantum mechanics.
Today, collision theory is not only a fundamental part of physics but also plays a crucial role in other fields such as chemistry, where it helps explain reaction rates and mechanisms.
What is a Collision?
A collision in physics is an event where two or more bodies exert forces on each other for a very short period. This interaction can result in a change in the motion and energy of the colliding bodies.
Imagine you’re playing a game of marbles, and you flick one marble toward another. When they hit each other, that’s a collision. In physics, a collision is when two or more objects come into contact with each other for a brief moment, exerting forces upon each other. This can cause the objects to change their motion, speed, or direction.
- Contact and Forces: During a collision, objects physically touch each other, and forces are applied. These forces are the result of the objects’ masses and the acceleration they experience during the impact.
- Change in Motion: Because of these forces, the objects might speed up, slow down, or change direction. The amount of change depends on the mass and velocity of the objects involved.
- Conservation of Momentum: One of the key principles in collisions is conserving momentum. This means the total momentum of all objects before the collision is equal to the total momentum after the collision.
- Energy Transfer: Collisions also involve the transfer of energy. The energy can be kinetic (movement energy), potential (stored energy), or other forms, like sound or heat.
In simple terms, a collision is like a brief but intense meeting between objects where they exchange forces and energy, leading to changes in their movement. It’s the physics version of a quick handshake or a high-five that can change the course of where the objects are heading!
Coefficient of Restitution
The coefficient of restitution (e) is a measure of the elasticity of a collision, representing the ratio of relative speeds after and before the impact. It ranges from 0 (perfectly inelastic) to 1 (perfectly elastic).
Imagine you’re playing basketball. When you bounce the ball on the ground, it bounces back up, but not to the height from which you dropped it. The Coefficient of Restitution (often abbreviated as “e”) is a number that tells us how bouncy a collision is. In physics, it’s a way to measure how much energy is conserved in a collision.
- Bounciness Scale: The Coefficient of Restitution is a value between 0 and 1. A value of 1 means the collision is perfectly elastic, like an ideal bouncy ball that bounces back to its original height without losing any energy. A value of 0 means the collision is perfectly inelastic, like a lump of clay that sticks to the ground without bouncing at all.
- Formula: The Coefficient of Restitution is calculated by taking the relative velocity of separation (how fast the objects move apart after the collision) and dividing it by the relative velocity of approach (how fast the objects come together before the collision). In symbols, if (v1) and (v2) are the velocities after the collision, and (u1) and (u2) are the velocities before the collision, the formula is:
\(\displaystyle e = \frac{v_2 – v_1}{u_1 – u_2} \)
- Perfectly Elastic Collision: In a perfectly elastic collision, ‘e’ would be 1, meaning no kinetic energy is lost. The objects would bounce off each other with the same relative speed but in opposite directions.
- Real-World Application: While a Coefficient of Restitution of 1 is rare in the real world, many sports like basketball or tennis rely on high restitution coefficients for the balls used in the games, ensuring they bounce well.
So, the Coefficient of Restitution is like a score for a collision’s efficiency in bouncing back.
Also Read: Laws of Motion
Types Of Collision
Collisions can be categorized based on how they conserve energy:
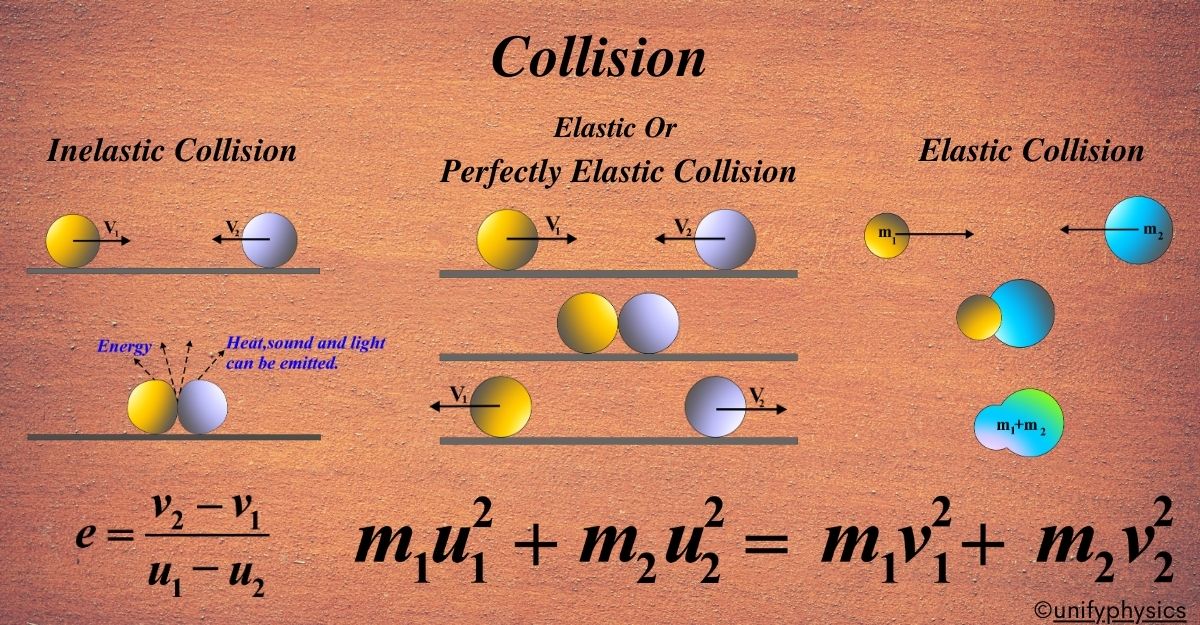
Elastic Or Perfectly Elastic Collision
An elastic collision is one where no kinetic energy is lost. The total momentum and total kinetic energy before and after the collision remains the same.
Think of an elastic collision like a super bouncy ball game. When you throw a bouncy ball against a wall, it hits the wall and bounces back without getting squished or losing its bounciness. That’s what we mean by an elastic collision in physics.
- No Energy Lost: In an elastic collision, when two objects hit each other, they might change direction or speed, but they don’t lose any of their ‘bounciness,’ which in physics terms is their kinetic energy. The total kinetic energy before and after the collision stays the same.
- Momentum Conserved: Just like energy, the total momentum (which is the mass of an object multiplied by its velocity) of the objects before they collide is the same as after they collide. It’s like the universe’s way of keeping the score even.
In the real world, it’s tough to find a perfectly elastic collision because some energy usually turns into sound or heat. But in physics problems, we often assume collisions are elastic to make things simpler.
A good example is a game of pool. When the cue ball smacks into another ball, they both zip away and if we ignore things like friction and air resistance, they keep their kinetic energy.
In an elastic collision, two objects collide and bounce off each other without any loss of kinetic energy. To understand this, we’ll use two key principles: conservation of momentum and conservation of kinetic energy.
Conservation of Momentum: Momentum is the product of mass and velocity. In any collision, the total momentum before the collision is equal to the total momentum after the collision. If we have two objects with masses (m1) and (m2), and velocities (u1) and (u2) before the collision, and velocities (v1) and (v2) after the collision, the conservation of momentum can be written as:
\(\displaystyle m_1u_1 + m_2u_2 = m_1v_1 + m_2v_2 \)
Conservation of Kinetic Energy: Kinetic energy is the energy of motion. In an elastic collision, the total kinetic energy is also conserved. The kinetic energy for each object is \(\displaystyle \frac{1}{2}mv^2 \), so for our two objects, the conservation of kinetic energy can be written as:
\(\displaystyle \frac{1}{2}m_1u_1^2 + \frac{1}{2}m_2u_2^2 = \frac{1}{2}m_1v_1^2 + \frac{1}{2}m_2v_2^2 \)
To find the final velocities after the collision, we need to solve these two equations together. We can simplify the kinetic energy equation by canceling the \(\displaystyle \frac{1}{2} \) from both sides:
\(\displaystyle m_1u_1^2 + m_2u_2^2 = m_1v_1^2 + m_2v_2^2 \)
Then, we can solve these equations to find expressions for (v1) and (v2) in terms of (m1), (m2), (u1), and (u2). The exact solution will depend on the initial conditions of the collision.
Through this derivation, students can see how the principles of conservation lead us to understand the outcomes of an elastic collision.
Coefficient of Restitution: Imagine you’re playing ping-pong and you drop the ball onto the table. It bounces back up, but not quite to the height from which you dropped it. The Coefficient of Restitution (often abbreviated as “e”) is a number that tells us how bouncy a collision is. In physics, it’s a way to measure how much energy is conserved in a collision.
The Coefficient of Restitution is a value between 0 and 1. A value of 1 means the collision is perfectly elastic, like an ideal bouncy ball that bounces back to its original height without losing any energy. A value of 0 means the collision is perfectly inelastic, like a lump of clay that sticks to the ground without bouncing at all.
The Coefficient of Restitution is calculated by taking the relative velocity of separation (how fast the objects move apart after the collision) and dividing it by the relative velocity of approach (how fast the objects come together before the collision). In symbols, if v1) and (v2) are the velocities after the collision, and (u1) and (u2) are the velocities before the collision, the formula is:
\(\displaystyle e = \frac{v_2 – v_1}{u_1 – u_2} \)
In a perfectly elastic collision, ‘e’ would be 1, meaning no kinetic energy is lost. The objects would bounce off each other with the same relative speed but in opposite directions.
While a Coefficient of Restitution of 1 is rare in the real world, many sports like basketball or tennis rely on high restitution coefficients for the balls used in the games, ensuring they bounce well. The Coefficient of Restitution is like a score for a collision’s efficiency in bouncing back.
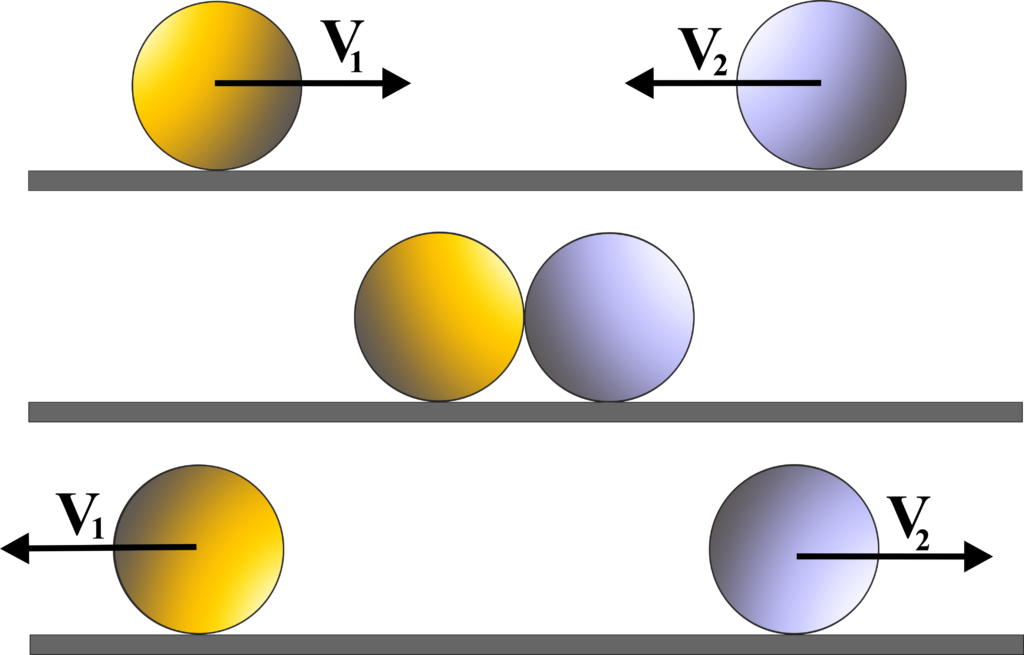
Inelastic Collision
In an inelastic collision, the objects do not stick together, but some kinetic energy is converted into other forms of energy, like heat or sound.
Imagine you’re playing with clay. If you throw one piece of clay at another, they squish together and don’t bounce apart. That’s similar to what happens in an inelastic collision.
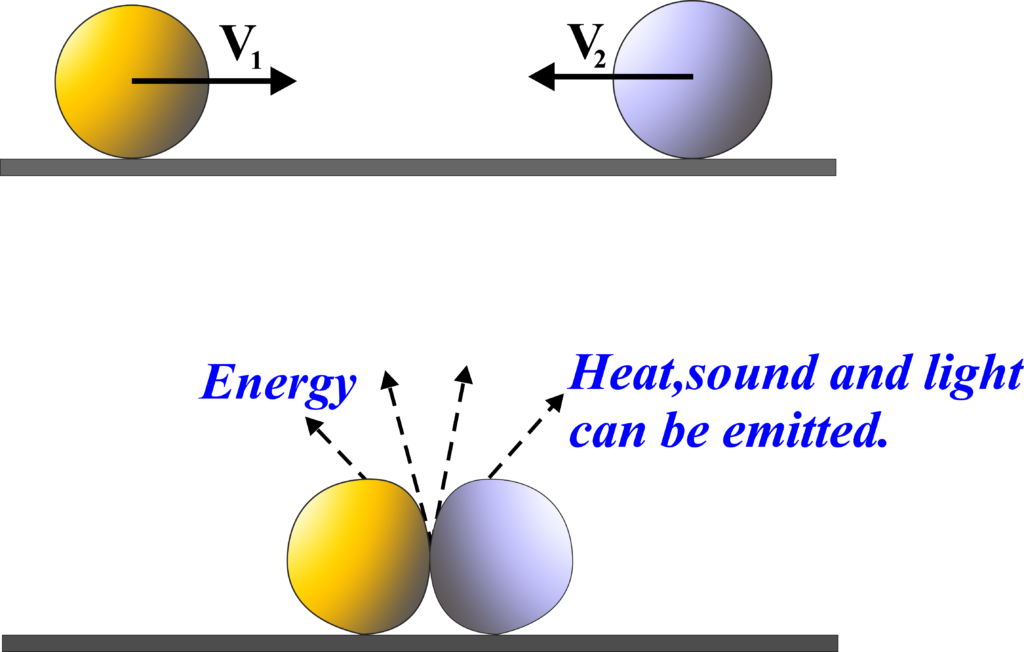
In an inelastic collision, when two objects collide, some of their kinetic energy (the energy due to motion) is transformed into other forms of energy, like heat or sound. This means they don’t bounce off each other as they would in an elastic collision.
Often, the objects might stick together after colliding, moving as a single unit. This is especially true in a perfectly inelastic collision, where the objects don’t separate at all after the impact.
Even though kinetic energy isn’t conserved, the total momentum of the system (the combined mass and velocity of the objects) is still conserved. This is a fundamental principle that holds true for all types of collisions.
Most collisions in everyday life are inelastic to some degree. For example, when cars crash, they crumple and might stick together, converting some of their kinetic energy into deforming the metal and generating heat.
In an inelastic collision, two objects collide and may stick together or not bounce perfectly, resulting in a loss of kinetic energy. However, the total momentum of the system is conserved.
Momentum is the product of mass and velocity. For two objects with masses (m1) and (m2), and velocities (u1) and (u2) before the collision, and a final combined velocity (v) after the collision (if they stick together), the conservation of momentum can be written as:
\(\displaystyle m_1u_1 + m_2u_2 = (m_1 + m_2)v \)
To find the final velocity after the collision, we use the conservation of momentum. Assuming the two objects stick together after the collision, we can set up the equation based on the initial velocities and masses:
Write down the initial momentum of both objects:
\(\displaystyle P_{initial} = m_1u_1 + m_2u_2 \)
Write down the final momentum, which is the sum of the masses times the final velocity since they stick together:
\(\displaystyle P_{final} = (m_1 + m_2)v \)
Set the initial momentum equal to the final momentum (since momentum is conserved):
\(\displaystyle m_1u_1 + m_2u_2 = (m_1 + m_2)v \)
Solve for (v), the final velocity:
\(\displaystyle v = \frac{m_1u_1 + m_2u_2}{m_1 + m_2} \)
This equation gives us the final velocity of the combined mass after a perfectly inelastic collision. It shows that even though the objects may not bounce apart, their combined momentum remains the same before and after the collision.
Through this derivation, students can understand how the conservation of momentum applies to inelastic collisions and how it can be used to calculate the outcome of such events. Remember, in real-world scenarios, some kinetic energy is transformed into other forms, like heat or sound, which is why these collisions are not perfectly elastic.
Coefficient of Restitution in Inelastic Collisions:
Think of a car crash where the cars crumple and don’t bounce back. This is an example of an inelastic collision. The Coefficient of Restitution (e) tells us how “bouncy” a collision is, but in inelastic collisions, things are a bit different.
In inelastic collisions, objects don’t bounce back perfectly. They might stick together or deform, which means they lose some kinetic energy as heat, sound, or deformation.
The Coefficient of Restitution is calculated by dividing the relative velocity of separation (how fast the objects move apart after the collision) by the relative velocity of approach (how fast the objects come together before the collision). In inelastic collisions, ‘e’ will always be less than 1, indicating that some kinetic energy is lost.
In a perfectly inelastic collision, the value of ‘e’ is 0 because the objects stick together and there is no bounce back at all. The relative velocity of separation is zero because the objects move together as one after the collision.
When a football player tackles another and they both fall to the ground together, it’s an inelastic collision. They don’t bounce off each other; instead, they lose some motion energy to the ground and to each other’s bodies.
The Coefficient of Restitution in inelastic collisions gives us a way to measure how much energy is lost when objects don’t bounce back completely.
Perfectly Inelastic Collision
This is a special case of inelastic collision where the colliding objects stick together after the impact, resulting in maximum loss of kinetic energy.
Imagine you’re making a snowman and you roll a small snowball into a larger one. The two snowballs stick together and become one bigger snowball. This is what happens in a perfectly inelastic collision.
- Sticking Together: In a perfectly inelastic collision, the objects that collide stick together and move as one after the collision. It’s like two pieces of gum squishing into one piece when they’re pressed together.
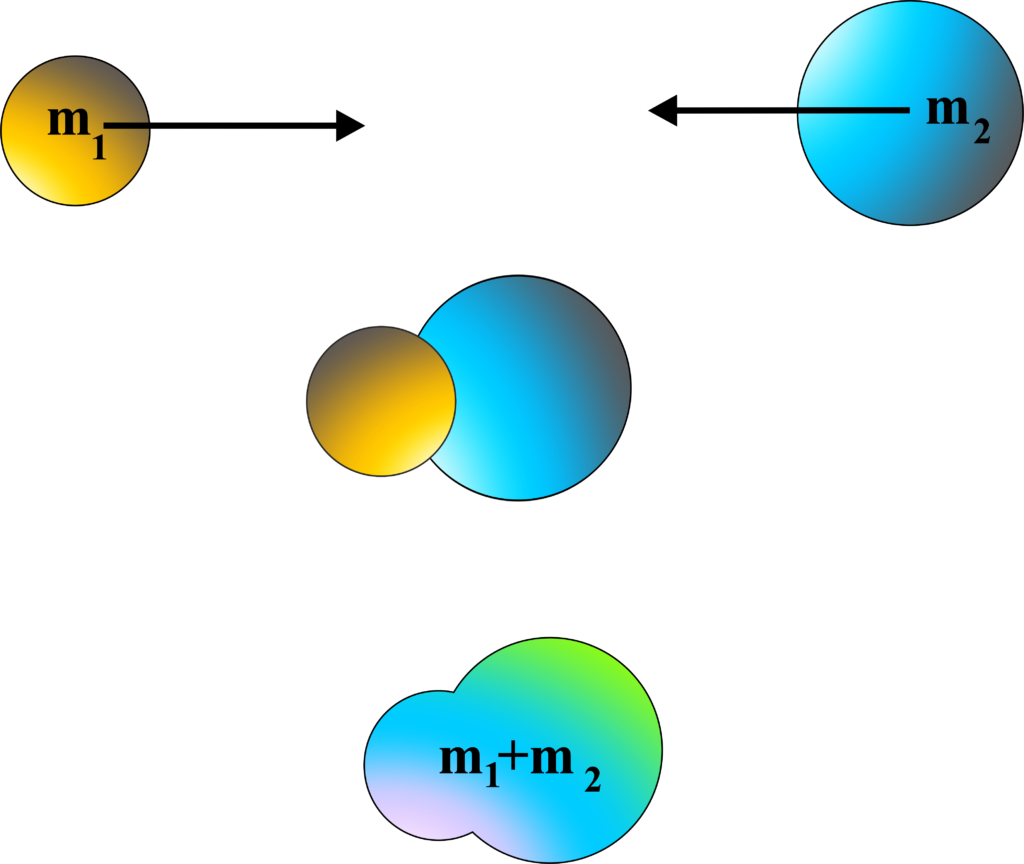
- Maximum Energy Loss: This type of collision results in the maximum amount of kinetic energy being lost compared to any other type of collision. The energy isn’t lost; it’s transformed into other forms, like heat or sound, or it goes into deforming the objects.
- Momentum Conserved: Even though kinetic energy changes, the system’s total momentum remains the same before and after the collision. It’s like the total weight of the snowballs before and after they stick together doesn’t change.
A common example is a car crash where the cars crumple and stick together upon impact. The kinetic energy is partly used up in bending the metal and partly dissipated as heat.
In simple terms, a perfectly inelastic collision is when two objects collide, stick together, and move as one, with some of their motion energy being converted into other forms of energy.
In a perfectly inelastic collision, two objects collide and stick together, moving as a single object afterward. The kinetic energy is not conserved, but momentum is.
Conservation of Momentum: Momentum before the collision must equal momentum after the collision. If we have two objects with masses (m1) and (m2), and velocities (u1) and (u2) before the collision, and they stick together to move with a common velocity (v) after the collision, the conservation of momentum can be expressed as:
\(\displaystyle m_1u_1 + m_2u_2 = (m_1 + m_2)v \)
To find the final common velocity ( v ) after the collision, we use the conservation of momentum principle: Write down the initial momentum of both objects:
\(\displaystyle P_{initial} = m_1u_1 + m_2u_2 \)
Write down the final momentum, which is the combined mass times the common velocity:
\(\displaystyle P_{final} = (m_1 + m_2)v \)
Set the initial momentum equal to the final momentum:
\(\displaystyle m_1u_1 + m_2u_2 = (m_1 + m_2)v \)
Solve for (v), the final common velocity:
\(\displaystyle v = \frac{m_1u_1 + m_2u_2}{m_1 + m_2} \)
This equation gives us the final velocity of the combined mass after a perfectly inelastic collision. It shows that the objects stick together and move with a velocity that is the mass-weighted average of their initial velocities.
Through this derivation, students can understand how momentum conservation applies to perfectly inelastic collisions and how it can be used to calculate the outcome of such events.
Coefficient of Restitution: Imagine you’re playing with modeling clay. If you throw two pieces together, they stick and don’t bounce apart. This is what happens in a perfectly inelastic collision.
- No Bounce Back: In a perfectly inelastic collision, the objects that collide stick together and move as one mass after the collision. There’s no bouncing back at all.
- Coefficient of Restitution (e): The Coefficient of Restitution measures how much bounce is involved in a collision. It’s calculated by comparing the speed of the objects moving apart after the collision to the speed at which they came together before the collision.
- Value of e: In a perfectly inelastic collision, the value of the Coefficient of Restitution is 0 because there is no bounce back—the objects stick together and move as one unit.
- Energy Transformation: Since there’s no bounce back, the kinetic energy isn’t conserved in the same way it is in an elastic collision. Instead, that energy goes into deforming the objects and other forms like heat or sound.
In simple terms, the Coefficient of Restitution in a perfectly inelastic collision tells us that the objects don’t bounce apart at all.
Difference Between Elastic and Inelastic Collision
The main difference lies in the conservation of kinetic energy. In an elastic collision, kinetic energy is conserved, while in an inelastic collision, some of the kinetic energy is transformed into other forms of energy.
| Aspect | Elastic Collision | Inelastic Collision |
|---|---|---|
| Kinetic Energy | Conserved. The total kinetic energy before and after the collision is the same. | Not conserved. Some kinetic energy is lost, often transformed into heat or sound. |
| Momentum | Conserved. The total momentum before and after the collision remains unchanged. | Conserved. The total momentum before and after the collision remains unchanged. |
| Object Behavior | Objects bounce off each other without any permanent deformation. | Objects may stick together or deform, and do not completely bounce apart. |
| Energy Conversion | No conversion of energy into other forms. | Kinetic energy is partly converted into other forms of energy like thermal or sound energy. |
| Real-World Likelihood | Less common. Perfectly elastic collisions are idealized and rare in the real world. | More common. Most real-world collisions are inelastic to some degree. |
| Examples | Collisions of atoms in a gas, billiard balls (nearly elastic). | Car crashes, football tackles. |
Collision in One Dimension
Head-On Collision
A head-on collision occurs when two objects move directly towards each other along a straight line. The conservation of momentum and, in elastic collisions, kinetic energy, can be used to determine the final velocities.
Imagine two toy cars on a track moving towards each other. If they crash directly into each other, that’s a head-on collision. In physics, a head-on collision is a type of collision where two objects move along a straight line towards each other and collide.
- Straight Line Motion: Both objects are moving along the same straight path, but in opposite directions, like two runners running towards each other on the same track.
- Impact: When they collide, they exert forces on each other. These forces are equal in magnitude and opposite in direction, according to Newton’s third law of motion.
- Momentum Conservation: The system’s total momentum (the combined momentum of both objects) is conserved. This means that the total momentum before the collision is equal to the total momentum after the collision.
- Energy: In an elastic head-on collision, the total kinetic energy is also conserved. However, in an inelastic head-on collision, some kinetic energy is converted into other forms of energy, like heat or sound.
- Calculations: To analyze a head-on collision, physicists use the conservation of momentum and, if the collision is elastic, the conservation of kinetic energy to calculate the final velocities of the objects after the collision.
A head-on collision in one dimension is like a direct confrontation between two objects on a single path, where they exchange momentum and possibly energy, depending on whether the collision is elastic or inelastic.
Collision in Two Dimensions
Oblique Collision
An oblique collision involves objects colliding at an angle. Unlike one-dimensional collisions, both the x and y components of momentum are conserved. This type of collision is common in billiards, where balls strike each other at various angles.
Imagine two cars at an intersection, one coming from the east and the other from the north. If they collide at the intersection, that’s an oblique collision. In physics, an oblique collision is when two objects collide at an angle that is not 90 degrees or 0 degrees to the line of impact.
- Angle of Collision: Unlike head-on collisions, where objects move directly toward each other, in oblique collisions, the objects approach each other at an angle.
- Two Components: Each object’s velocity can be split into two components: one parallel to the line of impact (the line joining the centers of the objects at the closest approach) and one perpendicular to it.
- Conservation Laws: The component of momentum parallel to the line of impact changes due to the collision, while the perpendicular component remains unchanged because no forces are acting in that direction.
- After the Collision: After the collision, the objects will move off at angles to their original paths. The final velocities and directions depend on the masses of the objects, their initial velocities, and the angle at which they collide.
- Calculations: To analyze an oblique collision, physicists use the conservation of momentum in both the parallel and perpendicular directions, along with the coefficient of restitution if the collision is elastic.
An oblique collision in two dimensions is like a dance where two partners approach each other at an angle, push, and twist away, each moving off in a new direction determined by their interaction.
Solved Examples:
Example 1: Two billiard balls, each of mass (0.2 kg), collide elastically. One ball is initially at rest while the other has an initial velocity of (2m/s). After the collision, the ball initially at rest moves off with a velocity of (1 m/s). Determine the final velocity of the other ball.
Solution: Given;
- Mass of each ball, (m = 0.2 kg)
- Initial velocity of one ball, (u1 = 0 m/s)
- Initial velocity of the other ball, (u2 = 2m/s)
- Final velocity of one ball, (v1 = 1 m/s)
By conservation of momentum in the horizontal direction:
\(\displaystyle m_1u_1 + m_2u_2 = m_1v_1 + m_2v_2 \)
\(\displaystyle 0.2 \times 0 + 0.2 \times 2 = 0.2 \times 1 + 0.2 \times v_2 \)
\(\displaystyle 0.4 = 0.2 + 0.2v_2 \)
\(\displaystyle 0.2v_2 = 0.4 – 0.2 \)
\(\displaystyle 0.2v_2 = 0.2 \)
\(\displaystyle v_2 = 1 \, \text{m/s} \)
Therefore, the final velocity of the other ball is (1 m/s).
Example 2: A (2 kg) ball moving with a velocity of (4 m/s) collides head-on with a (3 kg) ball moving in the opposite direction with a velocity of (3 m/s). If the collision is perfectly elastic, find the velocities of both balls after the collision.
Solution: Given;
- Mass of first ball, (m1 = 2 kg), (v1 = 4m/s)
- Mass of second ball, (m2 = 3 kg), (v2 = -3 m/s)
By conservation of momentum:
\(\displaystyle m_1v_1 + m_2v_2 = m_1v_{1f} + m_2v_{2f} \)
\(\displaystyle 2 \times 4 + 3 \times (-3) = 2 \times v_{1f} + 3 \times v_{2f} \)
\(\displaystyle 8 – 9 = 2v_{1f} – 3v_{2f} \)
\(\displaystyle -1 = 2v_{1f} – 3v_{2f} \)
By conservation of kinetic energy:
\(\displaystyle \frac{1}{2}m_1v_1^2 + \frac{1}{2}m_2v_2^2 = \frac{1}{2}m_1v_{1f}^2 + \frac{1}{2}m_2v_{2f}^2 \)
\(\displaystyle \frac{1}{2} \times 2 \times 4^2 + \frac{1}{2} \times 3 \times (-3)^2 = \frac{1}{2} \times 2 \times v_{1f}^2 + \frac{1}{2} \times 3 \times v_{2f}^2 \)
\(\displaystyle 16 + \frac{27}{2} = v_{1f}^2 + \frac{3}{2}v_{2f}^2 \)
\(\displaystyle 16 + \frac{27}{2} = v_{1f}^2 + \frac{3}{2}v_{2f}^2 \)
\(\displaystyle \frac{32 + 27}{2} = v_{1f}^2 + \frac{3}{2}v_{2f}^2 \)
\(\displaystyle \frac{59}{2} = v_{1f}^2 + \frac{3}{2}v_{2f}^2 \)
Solving these two equations simultaneously gives (v1f = 1 m/s) and (v2f} = -2m/s).
Example 3: A (2kg) block moving with a velocity of (4 m/s) collides with a stationary (3 kg) block. If the collision is perfectly inelastic, find the velocity of both blocks after the collision.
Solution: Given;
- Mass of first block, (m1 = 2 kg), (v1 = 4 m/s)
- Mass of second block, (m2 = 3 kg), (v2 = 0 m/s)
In a perfectly inelastic collision, the two objects stick together after the collision, so their final velocity (vf) is the same.
\(\displaystyle m_1v_1 + m_2v_2 = (m_1 + m_2)v_f \)
\(\displaystyle 2 \times 4 + 3 \times 0 = (2 + 3)v_f \)
\(\displaystyle 8 = 5v_f \)
\(\displaystyle v_f = \frac{8}{5} = 1.6 \, \text{m/s} \)
Therefore, both blocks move together with a velocity of (1.6 m/s) after the collision.
FAQs
What is a collision in physics, and how is it different from everyday use of the term?
In physics, a collision occurs when two or more objects come into contact and exert forces on each other for a short period of time. This can involve a change in motion, deformation, or transfer of energy between the objects. In everyday use, collision often refers to a physical impact or accident between objects.
What is the coefficient of restitution, and how is it calculated?
The coefficient of restitution (e) is a measure of how “bouncy” a collision is. It is defined as the ratio of the relative velocity of separation to the relative velocity of approach of two colliding objects. Mathematically, it is expressed as \(\displaystyle e = \frac{{v_{\text{final}} – v_{\text{initial}}}}{{u_{\text{initial}} – u_{\text{final}}}} \),
What characterizes an elastic or perfectly elastic collision?
In an elastic collision, both kinetic energy and momentum are conserved. This means that the total kinetic energy of the system before the collision is equal to the total kinetic energy after the collision. Additionally, the coefficient of restitution (e) for an elastic collision is equal to 1, indicating a perfect rebound without any loss of kinetic energy.
Can you explain the concept of an inelastic collision?
In an inelastic collision, kinetic energy is not conserved, but momentum is conserved. Some of the kinetic energy of the colliding objects is transformed into other forms of energy, such as thermal energy or deformation energy. The coefficient of restitution for an inelastic collision is less than 1, indicating a partial loss of kinetic energy.
What distinguishes a perfectly inelastic collision from other types of collisions?
In a perfectly inelastic collision, the colliding objects stick together after the collision and move as a single unit. Momentum is conserved in a perfectly inelastic collision, but kinetic energy is not. The coefficient of restitution for a perfectly inelastic collision is equal to 0, indicating a complete loss of kinetic energy.
Can you provide real-world examples of elastic and inelastic collisions?
An example of an elastic collision is the collision between billiard balls on a pool table. In this case, the balls rebound off each other with no loss of kinetic energy. An example of an inelastic collision is the collision between a car and a wall during a car crash. Some of the kinetic energy is transformed into deformation energy, causing damage to the car and the wall.
How does the coefficient of restitution affect the outcome of a collision?
The coefficient of restitution determines how “bouncy” a collision is. A higher coefficient of restitution (closer to 1) indicates a more elastic collision with less energy loss, while a lower coefficient (closer to 0) indicates a more inelastic collision with greater energy loss. The coefficient of restitution helps characterize the nature of the collision and its outcome.
What are the practical implications of understanding different types of collisions in engineering and everyday life?
Understanding different types of collisions is crucial in various fields, including engineering, automotive safety, and sports. Engineers use this knowledge to design safer vehicles and structures, while athletes and coaches use it to optimize performance and prevent injuries. Additionally, understanding collisions helps in accident reconstruction, forensic analysis, and improving product design and efficiency.