Combination of Capacitors

The journey of capacitors began in the 1740s with the invention of the Leyden jar. This was a simple device consisting of a glass jar filled with water and lined with metal on the inside and outside. It could store a high-voltage charge and was the first practical form of a capacitor. The Leyden jar was a crucial discovery that paved the way for the development of more sophisticated capacitors.

As technology progressed, the need for capacitors with different characteristics became apparent. The Leyden jar was limited in its capacity and safety, which led to the invention of capacitors with better materials and designs. The term “condenser” was initially used for these devices, reflecting their ability to condense electric charge.

The combination of capacitors emerged from the necessity to achieve specific capacitance values and voltage ratings not possible with a single capacitor. In the early days of electronics, it was discovered that connecting capacitors in different configurations could enhance their overall functionality.

Series and parallel combinations were the two primary methods developed to achieve the desired results. These combinations allowed for greater flexibility in designing circuits, especially in the burgeoning field of radio technology, where tuning and filtering were essential.

Today, capacitors are ubiquitous in electronic circuits. They come in various shapes, sizes, and materials, each suited for particular applications. The combination of capacitors remains a fundamental concept in circuit design, allowing engineers to tailor the capacitance and voltage characteristics to their specific needs.

Why is a Combination of Capacitors Needed?

In practical applications, sometimes a single capacitor doesn’t meet the required capacitance or voltage rating. By combining capacitors, we can achieve the desired capacitance and voltage handling capabilities for various electronic circuits.

Imagine you’re trying to fill a swimming pool with water. You could use a single large hose, but what if you don’t have one that’s big enough? Or what if you need to fill the pool more quickly? You might use several smaller hoses together to achieve your goal. This is similar to why we combine capacitors.

In electronics, capacitors are like hoses that “fill” with electric charge instead of water. Sometimes, a single capacitor doesn’t have enough “capacity” to hold the charge we need, or it can’t handle the voltage (pressure) in the circuit. Here’s why combining capacitors is essential:

• Achieving Desired Capacitance: Just like using multiple hoses to fill a pool faster, connecting capacitors in parallel gives us a larger total capacitance. This is useful when a circuit needs to store more charge.
• Voltage Requirements: Capacitors have a maximum voltage they can handle. By connecting capacitors in series, each one shares the voltage, allowing the combination to withstand higher voltages than any single capacitor could.
• Availability and Cost: It’s often easier and cheaper to use a combination of standard-value capacitors to get the precise capacitance needed for a circuit, rather than manufacturing a single capacitor with an unusual value.
• Redundancy and Reliability: In critical applications, using multiple capacitors can provide a backup if one fails, similar to having several paths for water to ensure the pool fills even if one hose gets blocked.

How are Capacitors Connected?

Capacitors can be connected in two primary ways: in series and parallel. The method of connection affects the total capacitance and the voltage distribution across the capacitors.

Think of capacitors like batteries in a flashlight. You can put them in different ways to get the light you need. Similarly, capacitors can be connected in two main ways to suit the needs of an electronic circuit:

Series Connection: Imagine lining up students for a school assembly. Each student’s hand is on the shoulder of the person in front. This is like capacitors in series—each one is connected to the next.

In this setup, the charge (Q) on each capacitor is the same, just like each student passes on the same message. The voltage (V) across each capacitor can be different, like each student having a different height.

The total capacitance (C_total) is less than any single capacitor’s capacitance. It’s like the message taking a longer path through each student, which takes more time.

Parallel Connection: Now, imagine students standing side by side, holding hands. This is like capacitors in parallel—each one is connected directly to the common points.

Here, the voltage across each capacitor is the same, like each student hearing the same announcement. The charge on each capacitor can be different, as each student might have a different reaction.

The total capacitance is the sum of all individual capacitances. It’s like the combined width of the students holding hands, which is wider than any single student. A series connection is used when the circuit needs to handle higher voltages, and a parallel connection is used when more storage capacity (capacitance) is needed.

Parallel Combination of Capacitors

When capacitors are connected in parallel, they have the same voltage across them but different charges.

When capacitors are connected in parallel:

• Each capacitor is connected to the same two points in the circuit, like multiple doors opening into the same room.
• The voltage (V) across each capacitor is the same because they’re all connected directly across the power source, just like all tanks would be filled to the same level from the same water source.
• The total charge (Q) stored is the sum of the charges on each capacitor. It’s like adding up the water in all tanks to get the total volume.
• The total capacitance (C_total) is the sum of all individual capacitances (\(\displaystyle C_{total} = C_1 + C_2 + C_3 + \ldots \)). This is because the effective area for storing charge increases, just like the total area for storing water increases with more tanks.

In a parallel combination, capacitors work together to store more charge at the same voltage. It’s a bit like a team of buckets collecting rainwater; each bucket collects the same amount of rain, but together, they collect much more than any single bucket could.

This arrangement is particularly useful when a circuit needs a large capacitance to store energy or to filter out noise at a certain voltage. It’s a common configuration in power supplies and audio circuits, where maintaining a stable voltage is crucial.

Parallel Combination of Capacitors Derivation: When capacitors are connected side by side, this is known as a parallel combination. Imagine you have several capacitors, each with a different capacity to store charge, like different-sized water tanks. You connect each capacitor across the same two points in a circuit, like connecting each tank to the same water pipeline.

The voltage (V) across each capacitor is the same because they’re all connected to the same two points, just like each water tank would be at the same water level. The charge (Q) on each capacitor can be different, depending on its capacitance (C), like how larger tanks can hold more water.

The total charge (Q_total) stored by the combination is the sum of the charges on each capacitor

\(\displaystyle Q_{total} = Q_1 + Q_2 + Q_3 + \ldots \)

Since charge (Q) is the product of capacitance (C) and voltage (V), we can write the charge on each capacitor as

\(\displaystyle Q_i = C_i \times V \)

Adding up the charges on all capacitors gives us the total charge:

\(\displaystyle Q_{total} = C_1 \times V + C_2 \times V + C_3 \times V + \ldots \)

The total capacitance (C_total) is defined as the total charge (Q_total) divided by the voltage (V):

\(\displaystyle C_{total} = \frac{Q_{total}}{V} \)

Substituting the expression for total charge, we get:

\(\displaystyle C_{total} = \frac{C_1 \times V + C_2 \times V + C_3 \times V + \ldots}{V} \)

Simplifying, we find that the voltage (V) cancels out:

\(\displaystyle C_{total} = C_1 + C_2 + C_3 + \ldots \)

So, the derived expression for the total capacitance of a parallel combination of capacitors is simply the sum of the capacitances of all the capacitors connected in parallel.

This means if you have capacitors with capacitances of 2F, 3F, and 5F connected in parallel, the total capacitance would be

\(\displaystyle C_{total} = 2F + 3F + 5F = 10F \)

How does this expression change if some capacitors have different voltages across them?

In a parallel combination of capacitors, the voltage across each capacitor is assumed to be the same because they are all connected to the same two points in the circuit. This common voltage is a fundamental characteristic of parallel circuits.

However, if capacitors with different voltage ratings are used in a parallel circuit, the maximum voltage that can be applied to the entire combination is limited by the capacitor with the lowest voltage rating. This is because the voltage across all capacitors in parallel is the same, and exceeding the lowest voltage rating could damage that capacitor.

The expression for the total capacitance in parallel does not change based on the voltage ratings of the capacitors. It remains the sum of the individual capacitances:

\(\displaystyle C_{total} = C_1 + C_2 + C_3 + \ldots \)

However, it’s crucial to ensure that the applied voltage does not exceed the lowest voltage rating among the capacitors to prevent any damage. So, while the capacitance formula remains the same, the practical application requires careful consideration of the voltage ratings when combining capacitors in parallel.

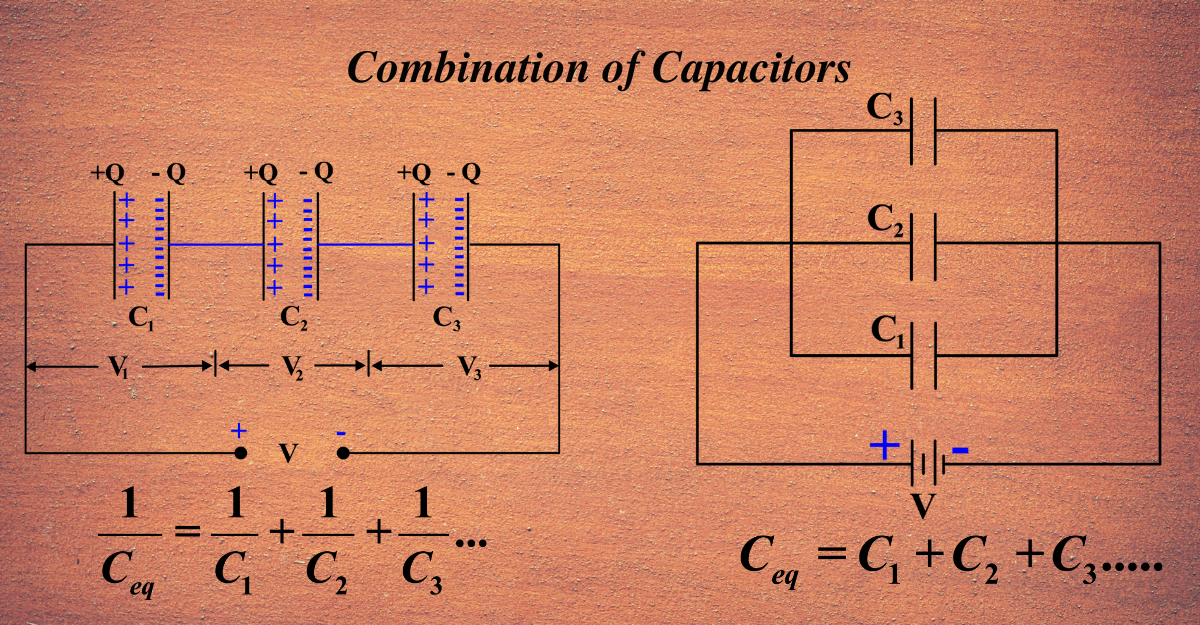
Series Combination of Capacitors

In a series connection, capacitors have the same charge but different voltages across them. The total capacitance is less than any individual capacitor’s capacitance. This arrangement is used when a lower total capacitance is required or when the capacitors need to withstand a higher voltage.

Think of a series of capacitors like a single-file line of students passing a basketball from one end to the other. Each student represents a capacitor, and the basketball represents the charge.

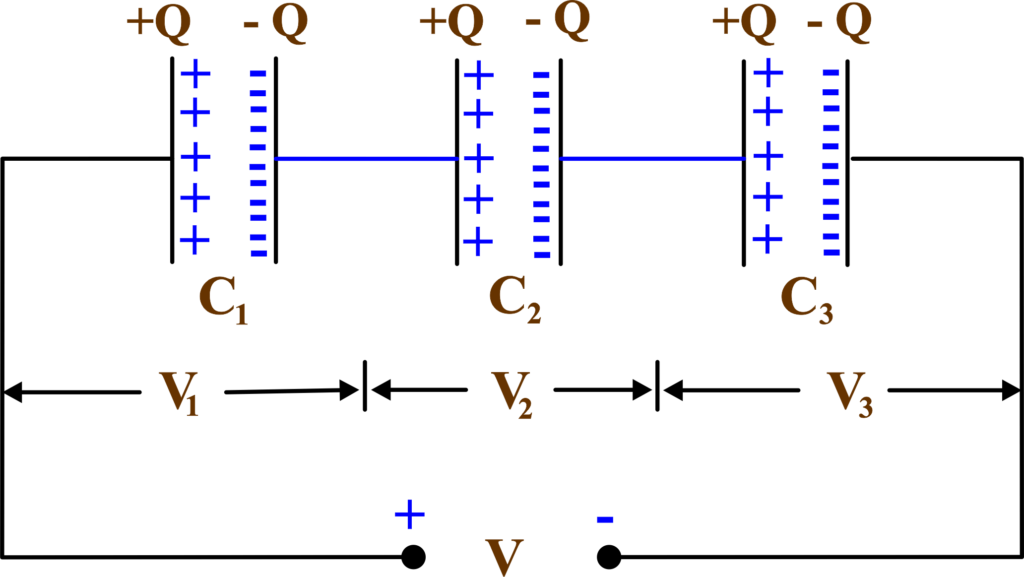
When capacitors are connected end-to-end, or in series:

• Each capacitor’s charge (Q) is the same, just like how each student touches the same basketball.
• The voltage (V) across each capacitor can differ, similar to how each student might hold the ball at a different height.
• The total voltage (V_total) across the combination is the sum of the voltages across each capacitor, just as the total distance the ball travels is the sum of the distances between each student.

The equivalent capacitance (C_eq) is the total capacitance you would need if you were to replace all the capacitors in series with just one capacitor that has the same effect. Unlike parallel combinations, the equivalent capacitance in series is not simply the sum of all capacitances. Instead, it’s a bit more complex because the capacitors share the charge.

Here’s the formula for the equivalent capacitance in a series combination:

\(\displaystyle \frac{1}{C_{eq}} = \frac{1}{C_1} + \frac{1}{C_2} + \frac{1}{C_3} + \ldots \)

Where ( \(\displaystyle C_1, C_2, C_3, \ldots \)) are the capacitances of the individual capacitors in series.

So, if you have three capacitors with capacitances of 2F, 3F, and 6F connected in series, the equivalent capacitance would be calculated as:

\(\displaystyle \frac{1}{C_{eq}} = \frac{1}{2F} + \frac{1}{3F} + \frac{1}{6F} \)

After finding a common denominator and adding the fractions, you would get:

\(\displaystyle \frac{1}{C_{eq}} = \frac{3}{6F} + \frac{2}{6F} + \frac{1}{6F} = \frac{6}{6F} \)

Therefore, the equivalent capacitance (C_eq ) is:

\(\displaystyle C_{eq} = \frac{6F}{6} = 1F \)

This means that the series combination can be replaced by a single capacitor of 1F, and it would have the same total charge and voltage characteristics as the original combination.

Series Combination of Capacitors Derivation: When capacitors are connected one after another, this is known as a series combination. Imagine you have several capacitors, and you want to connect them end-to-end, like train cars on a track. Each capacitor has its capacitance like each train car has its weight.

In a series circuit, the charge (Q) on each capacitor is the same, just like each train car would be pulled with the same force. The voltage (V) across each capacitor can be different, depending on its capacitance, like each train car might need a different push to move.

The total voltage (V_total) across the series combination is the sum of the voltages across each individual capacitor

\(\displaystyle V_{total} = V_1 + V_2 + V_3 + \ldots \)

Since voltage (V) is the charge (Q) divided by the capacitance (C), we can write the voltage across each capacitor as

\(\displaystyle V_i = \frac{Q}{C_i} \)

Adding up the voltages across all capacitors gives us the total voltage:

\(\displaystyle V_{total} = \frac{Q}{C_1} + \frac{Q}{C_2} + \frac{Q}{C_3} + \ldots \)

The total capacitance (C_total) is defined as the total charge (Q_total) divided by the total voltage (V_total):

\(\displaystyle C_{total} = \frac{Q}{V_{total}} \)

Substituting the expression for total voltage, we get:

\(\displaystyle C_{total} = \frac{Q}{\frac{Q}{C_1} + \frac{Q}{C_2} + \frac{Q}{C_3} + \ldots} \)

Simplifying, we find that the charge (Q) cancels out:

\(\displaystyle \frac{1}{C_{total}} = \frac{1}{C_1} + \frac{1}{C_2} + \frac{1}{C_3} + \ldots \)

The derived expression for the total capacitance of a series combination of capacitors is the reciprocal of the sum of the reciprocals of the capacitances of all the capacitors connected in series.

How voltage division rule apply to series capacitors?

The voltage division rule is a handy concept that applies to series capacitors, allowing us to determine the voltage across each capacitor when they are connected in series.

In a series circuit, all capacitors have the same charge (Q) because the charge has only one path to flow through.

Voltage Division: The voltage drop across each capacitor in a series is different and depends on its capacitance value. This is because the voltage (V) across a capacitor is given by the formula \(\displaystyle V = \frac{Q}{C} \). A capacitor with a smaller capacitance will have a larger voltage drop, and a capacitor with a larger capacitance will have a smaller voltage drop.

Applying Kirchhoff’s Voltage Law (KVL): According to KVL, the sum of the voltages across all capacitors in series equals the total applied voltage. So, if you know the total voltage and the capacitances of each capacitor, you can use the voltage division rule to find the voltage across any one of them.

To calculate the voltage across a specific capacitor in series, you can use the formula:

\(\displaystyle V_n = V_{total} \times \frac{C_{total}}{C_n} \)

where (V_n) is the voltage across the capacitor in question, (V_total) is the total voltage across the series, (C_total) is the equivalent capacitance of the series, and (C_n) is the capacitance of the specific capacitor.

Features of Series Combination of Capacitors

All capacitors in a series have the same charge. The equivalent capacitance of capacitors in series is smaller than the smallest individual capacitor’s capacitance in the group. This is because the total capacitance is the reciprocal of the sum of the reciprocals of each capacitor’s capacitance.

Same Charge on Each Capacitor: In a series circuit, every capacitor carries the same charge (Q). It’s like a relay race where each runner passes the same baton to the next.

Different Voltage Across Each Capacitor: The voltage across each capacitor in series can vary depending on its capacitance. It’s similar to runners in a relay race running different distances based on their speed.

Reduced Total Capacitance: The total capacitance of capacitors in series is less than the smallest individual capacitor’s capacitance. This is because the capacitors ‘share’ the charge, and the overall effect is like having a narrower path for charge flow.

Voltage Division: The total voltage across the series combination is divided among the capacitors. This is akin to dividing a long jump rope among several people, with each person holding a section of the rope.

Energy Storage: The energy stored in each capacitor is different because of the different voltages across them. However, the total energy stored in the series is the sum of the energies stored in each capacitor.

Failure Impact: If one capacitor in a series fails, it can break the circuit, much like a broken link in a chain that stops the entire chain from functioning.

High Voltage Applications: Series combinations are often used in high voltage applications because the voltage stress on each capacitor is reduced. It’s like distributing a heavy load among several people to make it easier to carry.

Also Read: Spherical Capacitor

Differences between Series and Parallel Grouping of Capacitors

Feature	Series Combination	Parallel Combination
Charge (Q)	The same voltage across each capacitor	Different charges can be stored on each capacitor
Voltage (V)	Different voltage across each capacitor	Same voltage across each capacitor
Total Capacitance (Ctotal)	\(\displaystyle \frac{1}{C_{total}} = \frac{1}{C_1} + \frac{1}{C_2} + \ldots \) (less than any individual capacitor’s capacitance)	\(\displaystyle C_{total} = C_1 + C_2 + \ldots \) (sum of individual capacitances)
Effect on Total Voltage (Vtotal)	The sum of voltages across each capacitor equals the total applied voltage	Voltage across each capacitor equals the applied voltage
Failure Impact	The voltage across each capacitor equals the applied voltage	Other capacitors can continue to function if one fails
Energy Storage	Energy is divided among capacitors based on their voltage	Energy stored is the sum of energies in each capacitor
Applications	Used when high voltage tolerance is needed	Used when high capacitance is required

This table summarizes the key differences between series and parallel combinations of capacitors, which are important for understanding how to use them effectively in various electronic circuits.

Solved Examples

Problem 1: Three capacitors with capacitances (C₁ = 2 µF), (C₂ = 4µF), and (C₃ = 6 µF) are connected in series. Calculate the equivalent capacitance of the combination.

Solution: For capacitors in series, the equivalent capacitance (C_eq) is given by:

\(\displaystyle \frac{1}{C_{eq}} = \frac{1}{C_1} + \frac{1}{C_2} + \frac{1}{C_3} \)

Calculate (C_eq):

\(\displaystyle \frac{1}{C_{eq}} = \frac{1}{2} + \frac{1}{4} + \frac{1}{6} \)
\(\displaystyle \frac{1}{C_{eq}} = \frac{6}{12} + \frac{3}{12} + \frac{2}{12} \)
\(\displaystyle \frac{1}{C_{eq}} = \frac{11}{12} \)
\(\displaystyle C_{eq} = \frac{12}{11} \)
\(\displaystyle C_{eq} \approx 1.09 \, \mu\text{F} \)

Therefore, the equivalent capacitance of the series combination is approximately (\(\displaystyle 1.09 \, \mu\text{F} \)).

Problem 2: Three capacitors with capacitances (C₁ = 3 µF), (C₂ = 6 µF), and (C₃ = 9 µF) are connected in parallel. Calculate the equivalent capacitance of the combination.

Solution: For capacitors in parallel, the equivalent capacitance (C_eq) is given by:

\(\displaystyle C_{eq} = C_1 + C_2 + C_3 \)

Calculate (C_eq):

\(\displaystyle C_{eq} = 3 + 6 + 9 \)
\(\displaystyle C_{eq} = 18 \, \mu\text{F} \)

Therefore, the equivalent capacitance of the parallel combination is (\(\displaystyle 18 \, \mu\text{F} \)).

Problem 3: Three capacitors with capacitances (C₁ = 2 µF), (C₂ = 3µF), and (C₃ = 6µF) are connected in series to a voltage supply of (V = 12 V). Calculate the voltage across the capacitor (C₂).

Solution: First, find the equivalent capacitance (C_eq) of the series combination:

\(\displaystyle \frac{1}{C_{eq}} = \frac{1}{C_1} + \frac{1}{C_2} + \frac{1}{C_3} \)
\(\displaystyle \frac{1}{C_{eq}} = \frac{1}{2} + \frac{1}{3} + \frac{1}{6} \)
\(\displaystyle \frac{1}{C_{eq}} = \frac{3}{6} + \frac{2}{6} + \frac{1}{6}\)
\(\displaystyle \frac{1}{C_{eq}} = 1 \)
\(\displaystyle C_{eq} = 1 \, \mu\text{F} \)

Next, calculate the total charge (Q) on the series combination:

\(\displaystyle Q = C_{eq} \cdot V \)
\(\displaystyle Q = 1 \, \mu\text{F} \cdot 12 \, \text{V} \)
\(\displaystyle Q = 12 \, \mu\text{C} \)

The voltage across (C₂) is given by:

\(\displaystyle V_2 = \frac{Q}{C_2}\)
\(\displaystyle V_2 = \frac{12 \, \mu\text{C}}{3 \, \mu\text{F}}\)
\(\displaystyle V_2 = 4 \, \text{V} \)

Therefore, the voltage across the capacitor (C₂) is (4 V).

Problem 4: Three capacitors with capacitances (C₁ = 5 µF), (C₂ = 10 µuF), and (C₃ = 15 µF) are connected in parallel to a voltage supply of (V = 20 V). Calculate the total energy stored in the combination.

Solution: First, find the equivalent capacitance (C_eq) of the parallel combination:

\(\displaystyle C_{eq} = C_1 + C_2 + C_3\)
\(\displaystyle C_{eq} = 5 + 10 + 15\)
\(\displaystyle C_{eq} = 30 \, \mu\text{F} \)

The energy stored in the capacitors is given by:

\(\displaystyle U = \frac{1}{2} C_{eq} V^2 \)

Calculate (U):

\(\displaystyle U = \frac{1}{2} \cdot 30 \, \mu\text{F} \cdot (20 \, \text{V})^2 \)
\(\displaystyle U = \frac{1}{2} \cdot 30 \times 10^{-6} \cdot 400 \)
\(\displaystyle U = 6 \times 10^{-3} \, \text{J} \)
\(\displaystyle U = 6 \, \text{mJ}\)

Therefore, the total energy stored in the parallel combination is (6 mJ).

Problem 5: Four capacitors with capacitances (C₁ = 4 µF), (C₂ = 6 µF), (C₃ = 8µF), and (C₄ = 12 µF) are connected as follows: (C₁) and (C₂) are in series, and (C₃) and (C₄) are in series. The series combinations are then connected in parallel. Calculate the equivalent capacitance.

Solution: First, find the equivalent capacitance of the series combinations:

\(\displaystyle \frac{1}{C_{12}} = \frac{1}{C_1} + \frac{1}{C_2} \)
\(\displaystyle \frac{1}{C_{12}} = \frac{1}{4} + \frac{1}{6} \)
\(\displaystyle \frac{1}{C_{12}} = \frac{3}{12} + \frac{2}{12} \)
\(\displaystyle \frac{1}{C_{12}} = \frac{5}{12} \)
\(\displaystyle C_{12} = \frac{12}{5} \)
\(\displaystyle C_{12} = 2.4 \, \mu\text{F} \)

\(\displaystyle\frac{1}{C_{34}} = \frac{1}{C_3} + \frac{1}{C_4} \)
\(\displaystyle\frac{1}{C_{34}} = \frac{1}{8} + \frac{1}{12} \)
\(\displaystyle\frac{1}{C_{34}} = \frac{3}{24} + \frac{2}{24} \)
\(\displaystyle \frac{1}{C_{34}} = \frac{5}{24} \)
\(\displaystyle C_{34} = \frac{24}{5} \)
\(\displaystyle C_{34} = 4.8 \, \mu\text{F} \)

Next, find the equivalent capacitance of the parallel combination:

\(\displaystyle C_{eq} = C_{12} + C_{34} \)
\(\displaystyle C_{eq} = 2.4 + 4.8 \)
\(\displaystyle C_{eq} = 7.2 \, \mu\text{F} \)

Therefore, the equivalent capacitance of the combination is (\(\displaystyle 7.2 \, \mu\text{F} \)).

Problem 6: Two capacitors with capacitances (C₁ = 5 µF) and (C₂ = 10 µF) are connected in series to a voltage supply of (V = 50 V). Calculate the charge on each capacitor.

Solution: First, find the equivalent capacitance (C_eq) of the series combination:

\(\displaystyle \frac{1}{C_{eq}} = \frac{1}{C_1} + \frac{1}{C_2} \)
\(\displaystyle \frac{1}{C_{eq}} = \frac{1}{5} + \frac{1}{10} \)
\(\displaystyle \frac{1}{C_{eq}} = \frac{2}{10} + \frac{1}{10}\)
\(\displaystyle \frac{1}{C_{eq}} = \frac{3}{10} \)
\(\displaystyle C_{eq} = \frac{10}{3} \)
\(\displaystyle C_{eq} = 3.33 \, \mu\text{F} \)

Next, calculate the total charge (Q) on the series combination:

\(\displaystyle Q = C_{eq} \cdot V \)
\(\displaystyle Q = 3.33 \, \mu\text{F} \cdot 50 \, \text{V} \)
\(\displaystyle Q = 166.5 \, \mu\text{C} \)

Since the charge is the same on capacitors in series, the charge on each capacitor (Q₁) and (Q₂) is (\(\displaystyle 166.5 \, \mu\text{C} \)). Therefore, the charge on each capacitor is (\(\displaystyle 166.5 \, \mu\text{C} \)).

FAQs