The concept of lenses has been around since ancient times. The first simple lenses were made from crystal or glass-like materials and were primarily used to magnify small objects or as burning glasses. During the 13th century, spectacles were invented in Italy, marking a significant advancement in lens technology. These were simple convex lenses designed to correct farsightedness.
The study of lenses took a scientific turn during the Renaissance. Scientists like Leonardo da Vinci and Johannes Kepler began to understand the principles of refraction and how lenses could be used to correct vision.
Kepler was the first to explain the process of vision and the use of both convex and concave lenses for correcting eyesight. He also laid the groundwork for the design of telescopes and microscopes, which would rely on the combination of lenses.
With the Industrial Revolution, lens-making saw significant improvements. Opticians were able to create more complex lens systems, combining thin lenses to reduce aberrations and enhance image quality. Today, the combination of lenses is a fundamental concept in optical devices such as cameras, microscopes, and telescopes. The precise combination of lenses allows for better control over magnification, focus, and image clarity.
What is a Lens?
A lens is a piece of transparent material, usually glass or plastic, with at least one curved surface that refracts, or bends, light rays. This property allows lenses to form images.
When light enters a lens, depending on the shape of the lens, it can either converge (come together) or diverge (spread out). This ability to change the direction of light allows lenses to form images. For example, when light rays enter a convex lens (which bulges outwards), they are bent in such a way that they meet at a point called the focus. On the other hand, a concave lens (which caves inwards) causes the light rays to spread out as if they were coming from a point.
The key thing about a lens is that it’s not just a piece of curved glass or plastic; it’s a carefully crafted tool that can manipulate light to achieve a specific result, like forming a clear image or focusing light to a point. This is why lenses are so important in devices that involve light, such as cameras, microscopes, and even our eyes.
A lens is a transparent object that refracts light to either converge or diverge rays, creating an image or focusing light. It’s a fundamental concept in physics and a crucial component in many optical devices.
Types of Lenses
In the world of optics, lenses are classified based on their shape and how they bend light. There are two main categories of lenses: convex and concave, explaining how their unique curvatures create distinct effects on light rays.
Concave Lens:
A concave lens is a “spreader” of light. It takes parallel rays and fans them out, which has the effect of making objects look smaller. Thinner at the center than at the edges, diverging light rays. Imagine the lens curving inward, like the inside of a spoon. This shape causes light rays that pass through the lens to spread out or diverge.
Here’s how it works: When parallel light rays enter a concave lens, they don’t converge to a point as they would with a convex lens. Instead, they bend outward, away from each other. This happens because the shape of the lens causes the light rays to bend at the edges more than in the center.
Now, because of this diverging effect, a concave lens cannot produce a real image where light converges. Instead, it creates what we call a virtual image. This virtual image is upright and smaller than the object itself, and it appears to be located on the same side of the lens as the object.
Type of Concave Lens: Concave lenses, which are also known as diverging lenses, come in different shapes based on their edges and surfaces. Here are the main types of concave lenses:
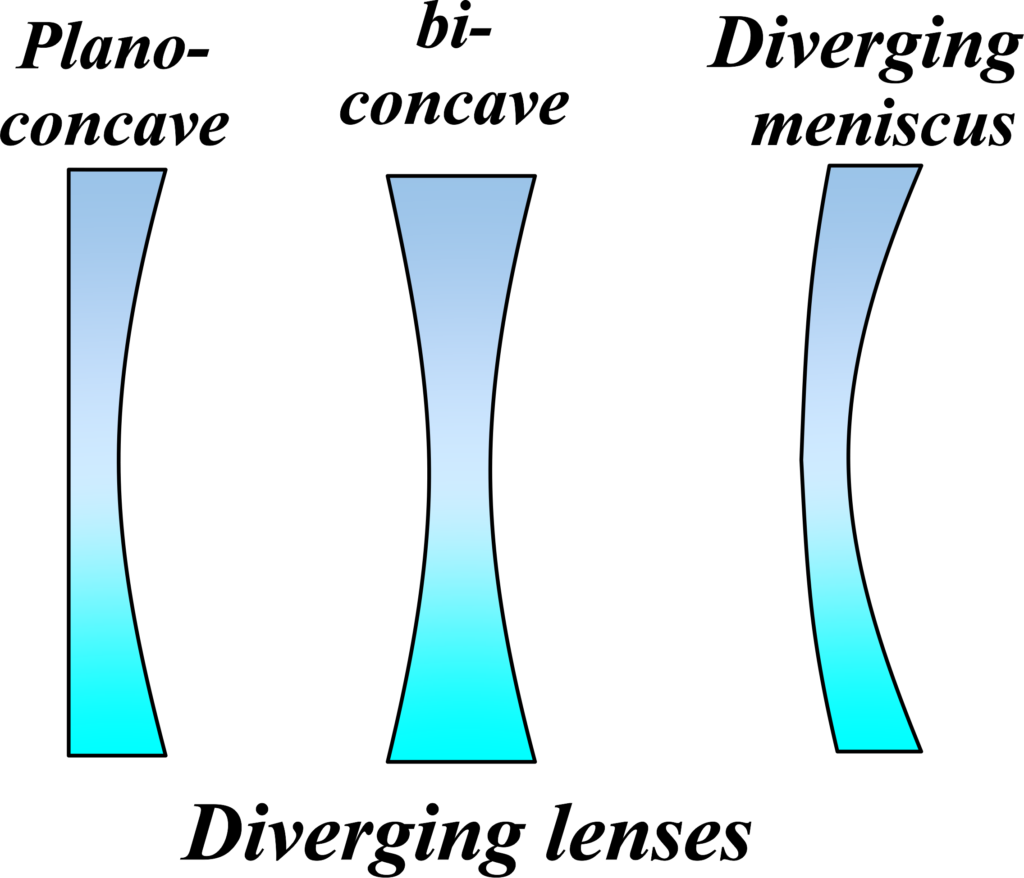
- Biconcave Lens: This type of lens is curved inward on both sides, resembling the shape of an hourglass. It’s symmetrical across both its horizontal and vertical axes.
- Plano-Concave Lens: This lens has one flat (planar) side and one concave side that curves inward. It looks like a flat disc with one side scooped out.
- Convexo-Concave Lens: Also known as a meniscus lens, this lens is curved inward on one side and less strongly curved outward on the other side. It combines the features of both convex and concave lenses.
Each type of concave lens diverges light rays that pass through it, but the extent and manner of divergence can vary based on the lens’s specific shape.
Convex Lens:
A convex lens is a transparent optical device that’s thicker in the middle and tapers to thinner edges. This bulging shape is key to its ability to bend light rays specially.
When parallel light rays enter a convex lens, they refract, or bend, towards each other and eventually converge at a point known as the focal point. The distance from the center of the lens to this focal point is called the focal length.
The converging property of a convex lens is what allows it to focus light, making it an essential component in many optical instruments. It’s the fundamental behavior of convex lenses that enables them to produce images, whether they’re magnified, reduced, or inverted, depending on the position of the object relative to the lens and its focal length.
A convex lens acts as a “gatherer” of light, bringing rays together to a focus, which is central to understanding how images are formed and manipulated in the field of optics.
Types of Convex Lenses: Convex lenses, also known as converging lenses, are designed to bring light rays together to a point. There are several types of convex lenses, each with a unique shape and function:
Bi-Convex Lens: This lens has both surfaces curved outward in a spherical shape. It’s symmetrical, meaning both sides of the lens have the same curvature, which allows it to focus light evenly from both sides.
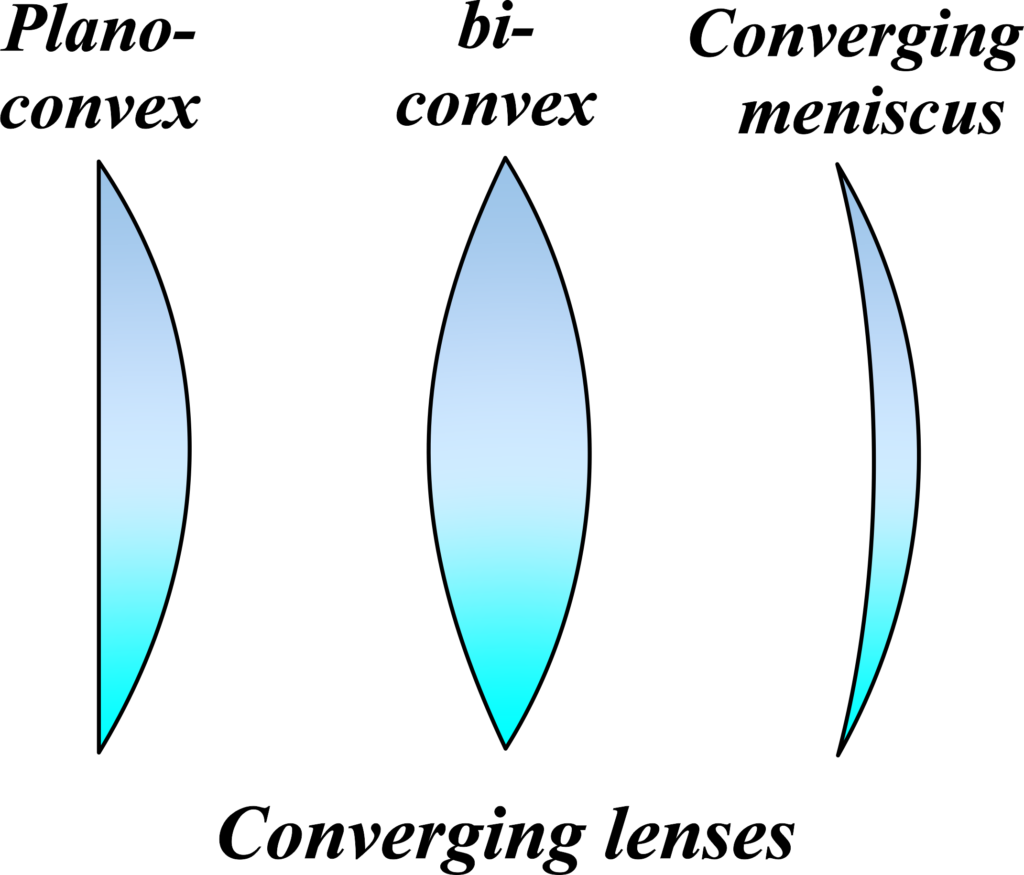
- Concavo-Convex Lens: Also known as a meniscus lens, this lens has one surface that is concave (curved inward) and one surface that is convex (curved outward). The curvature of the surfaces is designed to minimize certain optical aberrations.
- Plano-Convex Lens: This lens has one flat surface and one curved outward surface. It’s often used when the light enters from the flat side, focusing the light more on one side than the other.
What is a Combination of Lenses
It refers to two or more lenses placed in close proximity to affect the overall focal length and magnification, allowing for more precise control over image formation. The concept of a “Combination of Lenses” is quite fascinating in the world of optics. It refers to the process of aligning two or more lenses along a common axis so that they work together to manipulate light in a more complex way than a single lens could on its own.
When lenses are combined, their individual effects on light rays—such as bending, focusing, or spreading—are also combined. This means that the overall effect on light passing through multiple lenses is the sum of what each lens would do individually.
For instance, if you have two lenses, one that focuses light and another that spreads it out, when you put them together, the light will be affected by both actions. The light might be less focused than with just the focusing lens, or less spread out than with just the spreading lens, depending on the strengths and types of the lenses used.
Combining lenses allows us to fine-tune how we control light, giving us the ability to create more precise and varied optical outcomes. It’s like having a toolkit where each lens is a tool, and by using them in combination, we can achieve the desired visual effect.
Combination of Thin Lenses in Contact
When we talk about the “Combination of Thin Lenses in Contact,” we’re referring to a situation where two or more lenses are placed together so that their surfaces touch each other. This setup allows us to combine the optical effects of the individual lenses to achieve the desired overall effect on light passing through them.
Each lens has its focal length, which determines how it converges or diverges light. The focal length is a measure of how strongly the lens bends light rays. When lenses are in contact, their optical powers (the reciprocal of the focal length) add up. This is because the light passing through the first lens will immediately encounter the second lens, and the bending of light is a continuous process.
The formula to find the combined focal length (F) of two thin lenses in contact is:
\(\displaystyle \frac{1}{F} = \frac{1}{f_1} + \frac{1}{f_2} \)
where (f1) and (f2) are the focal lengths of the individual lenses.
The effective power of the combination is simply the sum of the powers of the individual lenses. If one lens has a power of +2 diopters and the other has a power of +3 diopters, the combined power is +5 diopters.
To derive the expression for the combination of thin lenses in contact, let’s consider two lenses with focal lengths (f1) and (f2), respectively. When these lenses are in contact, we can find the combined focal length (F ) of this lens system
For each lens, we use the lens formula, which relates the object distance (u), the image distance (v), and the focal length (f ):
\(\displaystyle \frac{1}{f} = \frac{1}{v} – \frac{1}{u} \)
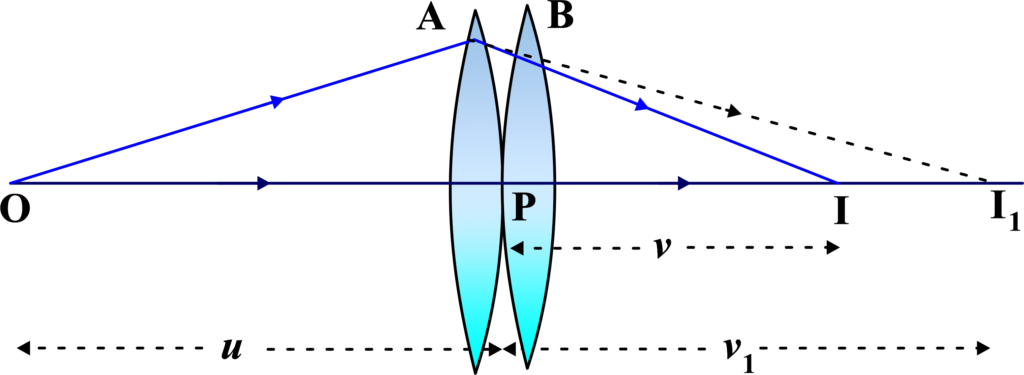
Consider two thin lenses (A) and (B) with focal lengths (f1) and (f2) respectively, placed in contact with each other. Object (O) is placed at a distance (u) from the lens (A). The image formed by a lens (A) is at (I1) with image distance (v1). This image (I1) serves as a virtual object for a lens (B), forming the final image at (I) with image distance (v).
For the first lens ( A ): Using the lens formula for a lens ( A ):
\(\displaystyle\frac{1}{v_1} – \frac{1}{u} = \frac{1}{f_1}\)
Rearrange this equation to find ( \(\displaystyle\frac{1}{v_1} \)):
\(\displaystyle\frac{1}{v_1} = \frac{1}{u} + \frac{1}{f_1}\)
For the second lens (B): The image formed by a lens (A) acts as a virtual object for a lens (B). Therefore, the object distance for a lens (B) is (v1), and the image distance for lens (B) is (v). Using the lens formula for lens (B):
\(\displaystyle\frac{1}{v} – \frac{1}{v_1} = \frac{1}{f_2}\)
Rearrange this equation to find (\(\displaystyle \frac{1}{v}\) ):
\(\displaystyle\frac{1}{v} = \frac{1}{v_1} + \frac{1}{f_2}\)
Now, we have two equations:
\(\displaystyle\frac{1}{v_1} = \frac{1}{u} + \frac{1}{f_1}\)
\(\displaystyle\frac{1}{v} = \frac{1}{v_1} + \frac{1}{f_2}\)
Substitute (\(\displaystyle \frac{1}{v_1}\) ) from the first equation into the second equation:
\(\displaystyle\frac{1}{v} = \left( \frac{1}{u} + \frac{1}{f_1} \right) + \frac{1}{f_2}\)
Simplify this equation to get:
\(\displaystyle\frac{1}{v} = \frac{1}{u} + \frac{1}{f_1} + \frac{1}{f_2}\)
For the system of lenses in contact, the combined focal length (f) is given by the lens formula:
\(\displaystyle\frac{1}{f} = \frac{1}{v} – \frac{1}{u}\)
Since ( \(\displaystyle\frac{1}{v} = \frac{1}{u} + \frac{1}{f_1} + \frac{1}{f_2}\) ), substitute into the lens formula:
\(\displaystyle\frac{1}{f} = \frac{1}{u} + \frac{1}{f_1} + \frac{1}{f_2} – \frac{1}{u}\)
The terms ( \(\displaystyle\frac{1}{u}\) ) cancel out:
\(\displaystyle\frac{1}{f} = \frac{1}{f_1} + \frac{1}{f_2}\)
Thus, the combined focal length (f) for two thin lenses in contact is given by:
\(\displaystyle\frac{1}{f} = \frac{1}{f_1} + \frac{1}{f_2}\)
This formula shows that the combined power of two thin lenses in contact is the sum of their powers.
For More Than Two Lenses In Contact:
When more than two thin lenses are placed in contact, the expression for the combined focal length can be extended to accommodate each additional lens. For three lenses with focal lengths (f1), (f2), and (f3), the combined focal length (F ) of the system is given by the formula:
\(\displaystyle \frac{1}{F} = \frac{1}{f_1} + \frac{1}{f_2} + \frac{1}{f_3} \)
This formula can be generalized for any number of lenses in contact. If you have (n) lenses with focal lengths (\(\displaystyle f_1, f_2, f_3, …, f_n \)), the combined focal length (F) is:
\(\displaystyle \frac{1}{F} = \frac{1}{f_1} + \frac{1}{f_2} + \frac{1}{f_3} + … + \frac{1}{f_n} \)
In this way, the power of the combined lens system is the sum of the powers of all the individual lenses. This principle allows for the creation of complex optical systems with precise control over the focusing properties.
Affect Of Arrangement of Lenses
The arrangement of lenses significantly affects their combined focal length. When lenses are combined, their focal lengths and the distances between them play a crucial role in determining the overall behavior of the lens system. Here’s how different arrangements can influence the combined focal length:
Lenses in Contact: For lenses that are in direct contact, their powers (the reciprocal of the focal lengths) simply add up. This is the simplest case and is described by the formula:
\(\displaystyle \frac{1}{F} = \frac{1}{f_1} + \frac{1}{f_2} \)
where (F) is the combined focal length, and (f1) and (f2) are the focal lengths of the individual lenses.
Lenses Separated by Distance: If there is a distance (d) between the lenses, the formula for the combined focal length (F) becomes:
\(\displaystyle \frac{1}{F} = \frac{1}{f_1} + \frac{1}{f_2} – \frac{d}{f_1 f_2} \)
The separation distance (d) introduces a correction factor that reduces the combined power of the lenses.
Sequential Arrangement: When lenses are arranged in sequence along the same optical axis, the combined focal length ( F ) can be found using the lens maker’s equation for multiple lenses. The light passes through each lens in turn, with each lens affecting the light based on its focal length and the distance to the next lens. If (f1), (f2), (f3), …, (fn) are the focal lengths of the individual lenses, the combined focal length (F) is given by:
\(\displaystyle \frac{1}{F} = \frac{1}{f_1} + \frac{1}{f_2} + \frac{1}{f_3} + \cdots + \frac{1}{f_n}\)
Parallel Arrangement: Although less common, if lenses could be arranged in parallel (side by side), each would affect a different part of the incoming light. The overall effect would be a combination of the individual effects, but this is not a typical setup in practical optics. This scenario is more complex, but we can consider the combined power of the lenses. If the focal lengths of the lenses in parallel are (f1), (f2), (f3), …, (fn), then the combined focal length (F) is given by the reciprocal of the sum of the reciprocals of the individual focal lengths:
\(\displaystyle\frac{1}{F} = \sum_{i=1}^n \frac{1}{f_i}\)
This formula is similar to the sequential arrangement because the contribution of each lens’s power is added together.
Converging and Diverging Lenses: The combination of converging (convex) and diverging (concave) lenses will result in a net focal length that depends on the strength and type of each lens. If a converging lens has a stronger power than a diverging lens, the system will still converge light, but less so than the converging lens alone.
When a converging lens (with focal length (f1 > 0)) and a diverging lens (with focal length (f2 < 0)) are placed in contact (or very close to each other), the combined focal length (F) is calculated using:
\(\displaystyle\frac{1}{F} = \frac{1}{f_1} + \frac{1}{f_2}\)
Here, (f1) is positive for the converging lens, and (f2) is negative for the diverging lens. These formulas help in determining the combined focal length for different configurations of lenses in optical systems.
Combination of Lenses
Case I (Same Focal Length):
When two thin lenses, one convex, and one concave, are placed in contact, their combined focal length can be determined using a specific formula.

The convex lens has a positive focal length, denoted as (+f ), and the concave lens has a negative focal length, denoted as (-f ). The power of a lens, (P), is the reciprocal of its focal length, (f). So, for the convex lens, the power is
for the convex lens, \(\displaystyle( P_{convex} = \frac{1}{+f} \)), and
for the concave lens, it’s \(\displaystyle( P_{concave} = \frac{1}{-f} \)).
When the lenses are in contact, their powers add up algebraically. The formula for the combined power, (P), is:
\(\displaystyle P = P_{convex} + P_{concave} \)
Substituting the values, we get:
\(\displaystyle P = \frac{1}{+f} + \frac{1}{-f} \)
If the lenses have the same focal length (f ), then the formula simplifies to:
\(\displaystyle P = \frac{1}{+f} – \frac{1}{+f} = 0 \)
This means the lenses have no net effect on the light passing through them, and the combination behaves like a plane glass plate with an equivalent focal length, (F), that is infinite, and power, (P), that is zero. To find the equivalent focal length (F ) for lenses with different focal lengths, you would use the combined power (P) and take its reciprocal:
\(\displaystyle F = \frac{1}{P} \)
If the lenses are separated by a distance ( d ), the equivalent focal length ( F ) is given by:
\(\displaystyle \frac{1}{F} = \frac{1}{f_1} + \frac{1}{f_2} – \frac{d}{f_1 f_2} \)
If both lenses have the same focal length, the equivalent focal length is half of the individual focal lengths.
Case II (Different Focal Length):
When two thin lenses, one convex with focal length ( f1 ) and one concave with focal length ( -f2 ), are put in contact, the formula to find the equivalent focal length ( F ) of the combination is given by:

\(\displaystyle\frac{1}{F} = \frac{1}{f_1} + \frac{1}{-f_2}\)
Since the concave lens has a negative focal length, we include the negative sign in the formula. Simplifying the equation, we get:
\(\displaystyle\frac{1}{F} = \frac{1}{f_1} – \frac{1}{f_2}\)
To find the equivalent focal length ( F ), you would take the reciprocal of the sum of the reciprocals of the individual focal lengths. If the focal lengths ( f1 ) and ( f2 ) are different, the combined focal length ( F ) will be a value that reflects the net optical power of the two lenses in contact.
For example, if ( f1 ) is 10 cm and ( f2 ) is -20 cm, the combined focal length ( F ) would be calculated as:
\(\displaystyle\frac{1}{F} = \frac{1}{10} – \frac{1}{20} = \frac{2 – 1}{20} = \frac{1}{20}\)
So, ( F ) would be 20 cm. This means the combination of the two lenses behaves like a single lens with a focal length of 20 cm. If ( f1 ) and ( f2 ) were equal in magnitude but opposite in sign, the combination would behave like a plane glass plate with no focusing power, as mentioned in your note. However, when their magnitudes are different, the combination will have a net focusing or diverging effect based on the dominant lens’s power.
Note: If (f2 > f1) then the combination will behave as a converging lens while the system will behave as diverging lens if ( f2 < f1 ).
Case III: When combining a plano-convex lens and a plano-concave lens made of different materials but with the same radius of curvature, we can determine the focal length of the combination using the Lensmaker’s formula.
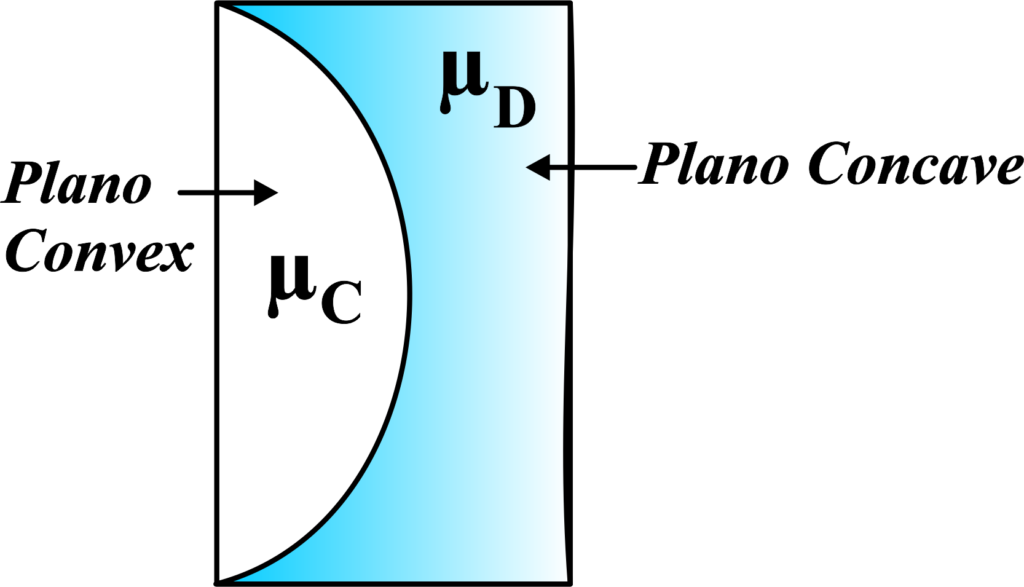
A plano-convex lens has one flat side and one convex side, while a plano-concave lens has one flat side and one concave side. The refractive index of the plano-convex lens is denoted by (µC), and for the plano-concave lens, it’s (µD). Both lenses have the same radius of curvature, denoted by (R).
The focal length of a lens depends on the refractive index of the material and the radius of curvature of its surfaces. For a plano-convex lens, the formula is:
\(\displaystyle \frac{1}{f_{convex}} = (\mu_C – 1) \left( \frac{1}{R} – \frac{1}{\infty} \right) \)
And for a plano-concave lens:
\(\displaystyle \frac{1}{f_{concave}} = (\mu_D – 1) \left( \frac{1}{\infty} – \frac{1}{-R} \right) \)
The combined focal length (F) of the system is given by:
\(\displaystyle \frac{1}{F} = \frac{1}{f_{convex}} + \frac{1}{f_{concave}} \)
Substituting the values from the individual formulas, we get:
\(\displaystyle \frac{1}{F} = (\mu_C – 1) \left( \frac{1}{R} \right) – (\mu_D – 1) \left( \frac{1}{R} \right) \)
Simplifying further:
\(\displaystyle \frac{1}{F} = \frac{\mu_C – \mu_D}{R} \)
Note:
- If (\(\displaystyle \mu_C > \mu_D \)), the system behaves as a converging lens.
- If (\(\displaystyle \mu_C < \mu_D\) ), the system behaves as a diverging lens.
To find the focal length ( F ), take the reciprocal of the combined power:
\(\displaystyle F = \frac{R}{\mu_C – \mu_D} \)
This formula helps students understand how the combination of a plano-convex and a plano-concave lens can be used to create a system with a specific focal length, depending on the materials’ refractive indices.
Case IV: When a convex lens is cut into two equal parts horizontally and these parts are put in contact, the combined focal length of the arrangement can be understood as follows:

The original convex lens has a focal length (f). When the lens is cut into two equal parts, each part becomes a lens with its focal length. Since each part is now effectively half the lens it was before, one might initially think that each part would have a focal length of (2f).
However, this is not the case because the curvature of each part remains unchanged. When the two halves are put back in contact, they work together as if they were never cut. This is because the two halves still form the same optical system as the original uncut lens. The combined focal length (F) of the two halves in contact is given by the formula:
\(\displaystyle\frac{1}{F} = \frac{1}{2f} + \frac{1}{2f} \)
Simplifying this, we get:
\(\displaystyle\frac{1}{F} = \frac{2}{2f} \)
Which further simplifies to:
\(\displaystyle\frac{1}{F} = \frac{1}{f} \)
Therefore, the combined focal length ( F ) is:
\(\displaystyle F = f \)
So, the combined focal length of the two halves in contact is the same as the focal length of the original uncut lens. This is because the optical power of a lens is determined by its curvature and the material from which it is made, both of which remain unchanged when a lens is cut and recombined in this manner. The halves in contact function optically the same as the original lens.
Case V: The concept of combined focal length is when an equi-convex lens is cut into two equal vertical parts and then reconfigured. We’ll consider different arrangements and their impact on the focal length.
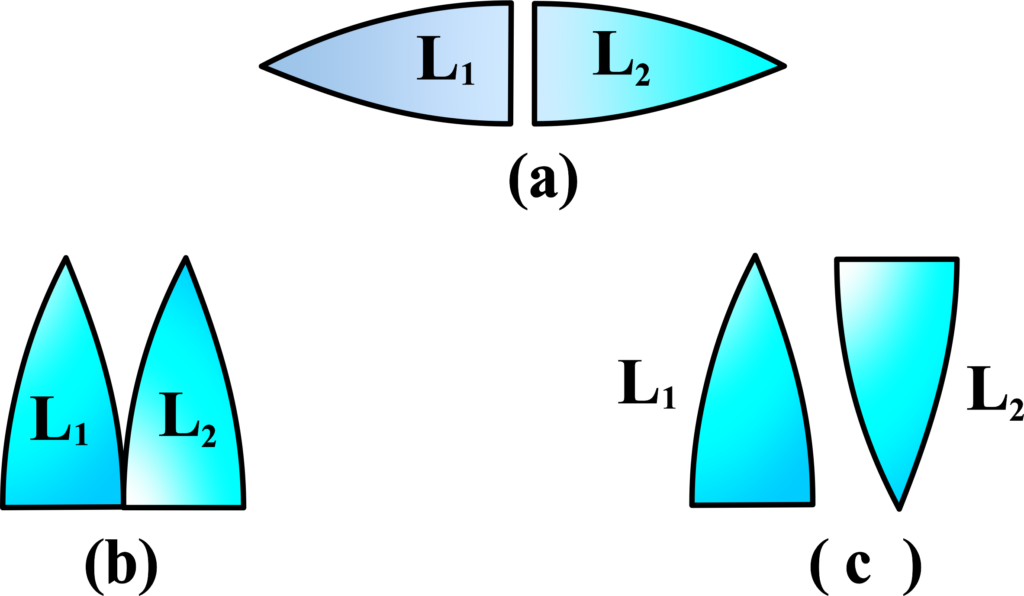
Start with an equi-convex lens (a lens with both surfaces curved outward). Cut it vertically into two halves. Place the two halves together with their flat surfaces touching (as shown in Figure (a)). The combined focal length of this arrangement can be calculated using the formula:
\(\displaystyle\frac{1}{F} = \frac{1}{f} + \frac{1}{f} = \frac{2}{f} \)
(f) is the original focal length of each half (since they are identical).
So, from figures (a) and (b) we can say that the combined focal length (F) will be half of the original focal length (f):
\(\displaystyle F = \frac{f}{2} \)
If the two halves are placed as shown in Figure (c), where one behaves as a converging lens and the other as a diverging lens: The converging effect of one half is negated by the diverging effect of the second inverted half. The resultant focal length of this combination is infinite (∞) because there is no net convergence or divergence (optical axis inversion).
The cutting and combination of lenses demonstrate how their properties affect the formation of images and the perceived quality of those images.
Focal Length of Different Types of Lenses
| Type of Lens | Equation for Focal Length (f) | Specific Value when μ=1.5 |
|---|---|---|
| Equi-Convex Lens | \(\displaystyle f = \frac{R}{(\mu – 1)}\) | ( f = R ) |
| Plano-Convex Lens | \(\displaystyle f = \frac{R}{2(\mu – 1)} \) | ( f = 2R ) |
| Equi-Concave Lens | \(\displaystyle f = -\frac{R}{(\mu – 1)} \) | ( f = -R ) |
| Plano-Concave Lens | \(\displaystyle f = -\frac{R}{2(\mu – 1)}\) | ( f = -2R) |
- ( R ): Radius of curvature.
- ( µ ): Refractive index (assumed to be 1.5 for all lenses).
Also Read: Refraction At A Spherical Surface
Applications
Combined lenses are used in various optical devices like microscopes, telescopes, cameras, and eyeglasses to improve image quality and magnification.
- Telescopes: In telescopes, lenses are combined to increase the magnification, allowing distant objects to appear closer and more detailed. The objective lens captures light from a distant object and creates an image, which is then magnified by the eyepiece lens for detailed observation.
- Microscopes: Similar to telescopes, microscopes use lens combinations to magnify small objects. An objective lens creates a magnified image of the specimen, which is further enlarged by the eyepiece lens, enabling us to see details that are not visible to the naked eye.
- Cameras: Camera lenses often consist of multiple lens elements working together to focus light onto the film or sensor. This combination helps in reducing optical aberrations and improving image clarity.
- Eyeglasses: For individuals with multiple vision problems, such as both nearsightedness and farsightedness, bifocal or multifocal glasses combine different lenses to correct each issue within a single pair of glasses.
- Optical Instruments: Many precision optical instruments, like rangefinders and binoculars, use combinations of lenses to achieve the desired focus and magnification while minimizing distortions.
Solved Examples
Example 1: Two thin lenses, one with a focal length of (\(\displaystyle f_1 = 10 \text{ cm}\)) and the other with a focal length of (\(\displaystyle f_2 = -15 \text{ cm}\)), are placed in contact. Calculate the focal length of the combination.
Solution: The focal length of the combination (F) of two lenses in contact is given by:
\(\displaystyle\frac{1}{F} = \frac{1}{f_1} + \frac{1}{f_2}\)
Substitute the values:
\(\displaystyle\frac{1}{F} = \frac{1}{10} + \frac{1}{-15}\)
\(\displaystyle\frac{1}{F} = \frac{3 – 2}{30}\)
\(\displaystyle\frac{1}{F} = \frac{1}{30}\)
\(\displaystyle F = 30 \text{ cm}\)
The focal length of the combination is 30 cm.
Example 2: Two lenses with powers (\(\displaystyle P_1 = 5 \text{ D}\)) and (\(\displaystyle P_2 = -3 \text{ D}\)) are placed in contact. Calculate the power and the focal length of the combination.
Solution: The power (P) of the combination of two lenses in contact is given by:
\(\displaystyle P = P_1 + P_2\)
Substitute the values:
\(\displaystyle P = 5 + (-3) = 2 \text{ D}\)
The focal length (F) is given by:
\(\displaystyle F = \frac{1}{P} = \frac{1}{2} = 0.5 \text{ m} = 50 \text{ cm}\)
The power of the combination is 2 D and the focal length is 50 cm.
Example 3: An object is placed 30 cm from a convex lens of focal length 20 cm. A concave lens of focal length -15 cm is placed in contact with the convex lens. Calculate the position of the final image.
Solution: First, calculate the combined focal length (F) of the lenses:
\(\displaystyle\frac{1}{F} = \frac{1}{f_1} + \frac{1}{f_2}\)
Substitute the values:
\(\displaystyle\frac{1}{F} = \frac{1}{20} + \frac{1}{-15}\)
\(\displaystyle\frac{1}{F} = \frac{3 – 4}{60}\)
\(\displaystyle\frac{1}{F} = \frac{-1}{60}\)
\(\displaystyle F = -60 \text{ cm}\)
Now use the lens formula for the combination:
\(\displaystyle\frac{1}{F} = \frac{1}{v} – \frac{1}{u}\)
Given: (u = -30 cm) (object distance, negative)
Substitute the values:
\(\displaystyle\frac{1}{-60} = \frac{1}{v} – \frac{1}{-30}\)
\(\displaystyle\frac{1}{-60} = \frac{1}{v} + \frac{1}{30}\)
\(\displaystyle\frac{1}{v} = \frac{1}{-60} – \frac{1}{30}\)
\(\displaystyle\frac{1}{v} = \frac{-1 – 2}{60}\)
\(\displaystyle\frac{1}{v} = \frac{-3}{60}\)
\(\displaystyle v = -20 \text{ cm}\)
The final image is formed 20 cm on the same side of the lens as the object, indicating a virtual image.
Example 4: An object 5 cm high is placed 25 cm from a combination of two lenses in contact: a convex lens of focal length 15 cm and a concave lens of focal length -10 cm. Calculate the height of the final image.
Solution: First, calculate the combined focal length (F):
\(\displaystyle\frac{1}{F} = \frac{1}{f_1} + \frac{1}{f_2}\)
Substitute the values:
\(\displaystyle\frac{1}{F} = \frac{1}{15} + \frac{1}{-10}\)
\(\displaystyle\frac{1}{F} = \frac{2 – 3}{30}\)
\(\displaystyle\frac{1}{F} = \frac{-1}{30}\)
\(\displaystyle F = -30 \text{ cm}\)
Now use the lens formula:
\(\displaystyle\frac{1}{F} = \frac{1}{v} – \frac{1}{u}\)
Given: u = -25 cm
Substitute the values:
\(\displaystyle\frac{1}{-30} = \frac{1}{v} – \frac{1}{-25}\)
\(\displaystyle\frac{1}{-30} = \frac{1}{v} + \frac{1}{25}\)
\(\displaystyle\frac{1}{v} = \frac{1}{-30} – \frac{1}{25}\)
\(\displaystyle\frac{1}{v} = \frac{-5 – 6}{150}\)
\(\displaystyle\frac{1}{v} = \frac{-11}{150}\)
\(\displaystyle v = -\frac{150}{11} \approx -13.64 \text{ cm}\)
Calculate the magnification (m):
\(\displaystyle m = \frac{v}{u} = \frac{-13.64}{-25} \approx 0.5456\)
Calculate the height of the image (hi):
\(\displaystyle h_i = m \times h_o = 0.5456 \times 5 \text{ cm} \approx 2.73 \text{ cm}\)
The height of the final image is approximately 2.73 cm, indicating an upright and reduced image.
Example 5: Two thin lenses, one with a focal length of (\(\displaystyle f_1 = 10 \text{ cm} \)) (convex) and the other with a focal length of ( \(\displaystyle f_2 = -20 \text{ cm}\) ) (concave), are placed in contact in water (refractive index = 1.33). Calculate the effective focal length of the combination.
Solution: The effective focal length (F) in water is given by:
\(\displaystyle\frac{1}{F} = \frac{1}{f_1} + \frac{1}{f_2}\)
Substitute the values:
\(\displaystyle\frac{1}{F} = \frac{1}{10} + \frac{1}{-20}\)
\(\displaystyle\frac{1}{F} = \frac{2 – 1}{20}\)
\(\displaystyle\frac{1}{F} = \frac{1}{20}\)
\(\displaystyle F = 20 \text{ cm}\)
The effective focal length of the combination in water is 20 cm.
Example 6: Three lenses with powers (\(\displaystyle P_1 = 2 \text{ D}\)), (\(\displaystyle P_2 = 1 \text{ D}\)), and (\(\displaystyle P_3 = -1.5 \text{ D}\)) are placed in contact. Calculate the power and the focal length of the combination.
Solution: The power (P) of the combination of three lenses in contact is given by:
\(\displaystyle P = P_1 + P_2 + P_3\)
Substitute the values:
\(\displaystyle P = 2 + 1 – 1.5 = 1.5 \text{ D}\)
The focal length (F) is given by:
\(\displaystyle F = \frac{1}{P} = \frac{1}{1.5} \approx 0.67 \text{ m} = 67 \text{ cm}\)
The power of the combination is 1.5 D and the focal length is 67 cm.
FAQs
What is meant by the combination of lenses in contact, and why is it used?
The combination of lenses in contact refers to placing two or more thin lenses close together along the same optical axis so that they act as a single optical system. This setup is used to achieve desired optical properties, such as a specific focal length or magnification, that cannot be obtained with a single lens.
How does the arrangement of lenses affect the overall focal length of the combination?
The arrangement of lenses affects the overall focal length because the effective focal length of a combination of lenses depends on the individual focal lengths and the distances between them. For lenses in contact, the overall focal length can be calculated based on the focal lengths of the individual lenses. This determines how the combined lenses bend light and form images.
What are some practical applications of using combinations of lenses?
Combinations of lenses are used in various practical applications, including microscopes, telescopes, cameras, and corrective eyeglasses. In microscopes and telescopes, lens combinations provide high magnification and improved image quality. In cameras, they help achieve focus and control aberrations. Corrective eyeglasses use combinations to address complex vision problems.
How do you determine the focal length of a combination of convex and concave lenses?
The focal length of a combination of convex and concave lenses is determined by considering the individual focal lengths and how they interact when placed in contact. The overall focal length can be positive or negative, depending on the relative strengths and positions of the convex (converging) and concave (diverging) lenses.
What are the advantages of using a combination of lenses over a single lens?
Using a combination of lenses offers several advantages, including the ability to fine-tune optical properties like focal length and magnification, reduce optical aberrations, and improve image quality. Combinations can also provide greater flexibility in designing optical systems to meet specific requirements that a single lens cannot achieve.
What is the effect of combining multiple lenses on the image formation process?
Combining multiple lenses affects the image formation process by altering the path of light rays through the optical system. This can result in changes to image size, orientation, and quality. Properly designed combinations can enhance image clarity, reduce distortions, and achieve desired magnification levels, making them essential in advanced optical instruments.
Can you explain how the focal length of different types of lenses (convex and concave) impacts their combination?
The focal length of different types of lenses impacts their combination by determining the overall behavior of the optical system. Convex lenses have positive focal lengths and converge light rays, while concave lenses have negative focal lengths and diverge light rays. When combined, the resulting focal length depends on the balance between these converging and diverging effects, influencing whether the system acts as a converging or diverging lens overall.
