Conservation of Mechanical Energy

The concept of energy conservation is not new; it has been pondered upon since ancient times. The earliest inklings of this idea can be traced back to philosophers like Thales of Miletus and Empedocles, who lived around 550 BCE and 490–430 BCE, respectively. They explored the fundamental principles of what we now understand as the conservation of mass energy.

Fast forward to the 17th century, and we meet Gottfried Leibniz, a mathematician and philosopher who made significant strides in our understanding of energy. Between 1676 and 1689, Leibniz was the first to attempt a mathematical formulation of the kind of energy associated with motion, which we now call kinetic energy. He used the work of Christiaan Huygens on collision and noticed that in many mechanical systems, a certain quantity (which we now know as energy) was conserved as long as the objects did not interact.

This early work laid the groundwork for the principle of conservation of mechanical energy, which states that in an isolated system, the total mechanical energy remains constant if only conservative forces are at play. This principle was further developed by scientists like Julius Robert von Mayer and James Prescott Joule in the 19th century, who showed that energy could be converted from one form to another but not created or destroyed.

What is Mechanical Energy?

Mechanical energy refers to the sum of two types of energy within a system: kinetic energy and potential energy. Conceptually, it encompasses the energy associated with the motion and position of objects within a mechanical system.

Kinetic energy is the energy an object possesses due to its motion, while potential energy is the energy stored within an object due to its position or configuration within a system. When these two forms of energy are combined, they constitute the mechanical energy of the system.

Mechanical energy is a crucial concept in physics as it provides a comprehensive understanding of how energy is distributed and transformed within mechanical systems. It allows us to analyze the behavior of objects in motion and understand the interplay between motion and position in determining the overall energy state of a system.

Types of Mechanical Energy

There are two main types of mechanical energy:

Kinetic Energy

The energy an object has because of its motion. For example, a rolling ball has kinetic energy. Kinetic Energy is the energy of motion. Anything that moves has kinetic energy, from the smallest ant scurrying across the ground to the largest airplane soaring in the sky. It’s the energy that an object possesses because it’s moving.

The faster something moves, the more kinetic energy it has. It’s like when you’re cycling; the harder you pedal, the faster you go, and the more kinetic energy you have. This energy comes from the work done to get the object moving in the first place.

The formula for kinetic energy is:

\(\displaystyle KE = \frac{1}{2} m v^2 \)

• (KE) stands for Kinetic Energy.
• (m) is the mass of the object (how much stuff is in it).
• (v) is the velocity of the object (how fast it’s going).

Example: If you have a ball with a mass of 0.5 kg and it’s rolling at a velocity of 2 meters per second, its kinetic energy would be:

\(\displaystyle KE = \frac{1}{2} \times 0.5 \, \text{kg} \times (2 \, \text{m/s})^2 \)
\(\displaystyle KE = \frac{1}{2} \times 0.5 \, \text{kg} \times 4 \, \text{m}^2/\text{s}^2 \)
\(\displaystyle KE = 2 \, \text{J} \)

This means the ball has 2 joules of energy because it’s moving. Kinetic energy is crucial because it’s involved in everything that moves. Understanding it helps us figure out how much work an object can do because of its motion. It’s a key part of many calculations in physics, from understanding car crashes to playing sports.

Potential Energy

The energy an object has because of its position or configuration. For example, a book on a high shelf has potential energy due to gravity. Potential Energy is like the energy savings account of an object. It’s the energy that’s stored because of where the object is or how it’s set up. For example, a diver on a diving board has potential energy because of their position high above the pool.

The idea is simple: the higher you lift something against gravity, the more potential energy it has. It’s like lifting a backpack full of books to the top of a staircase; the higher you go, the more energy you’re storing in that backpack.

The formula for calculating potential energy, especially gravitational potential energy, is:

\(\displaystyle PE = m \times g \times h \)

• (PE) is the Potential Energy.
• (m) is the mass of the object (how heavy it is).
• (g) is the acceleration due to gravity (usually about ( 9.8 m/s²) on Earth).
• (h) is the height above the ground (how high you’ve lifted the object).

Example: If you have a rock that weighs 1 kg and you lift it 5 meters off the ground, its potential energy would be:

\(\displaystyle PE = 1 \, \text{kg} \times 9.8 \, \text{m/s}^2 \times 5 \, \text{m} = 49 \, \text{J} \)

This means the rock has 49 joules of energy stored in it because of its position. Potential Energy is important because it’s the starting point for all motion. It’s what gives a roller coaster the ability to zoom down the tracks and what powers a clock’s pendulum. Understanding potential energy helps us predict how objects will behave when they start moving.

Conservation of Mechanical Energy

The principle of conservation of mechanical energy states that the total mechanical energy (kinetic plus potential) in an isolated system remains constant if only conservative forces (like gravity) are doing work. This means that energy can neither be created nor destroyed; it can only be transformed from one form to another.

Imagine you’re at a skate park. You skate up a ramp, and at the top, you pause for a moment before skating down. At the top of the ramp, you have a lot of potential energy because of your height. As you skate down, that potential energy is converted into kinetic energy, which is the energy of motion. By the time you reach the bottom of the ramp, all the potential energy has turned into kinetic energy, and you’re moving at your fastest.

Here’s the cool part: the total amount of energy you have (potential plus kinetic) doesn’t change from the top of the ramp to the bottom. This is what we mean by the conservation of mechanical energy. The energy changes forms but the total amount stays the same, as long as no other forces (like friction or air resistance) are doing work on you.

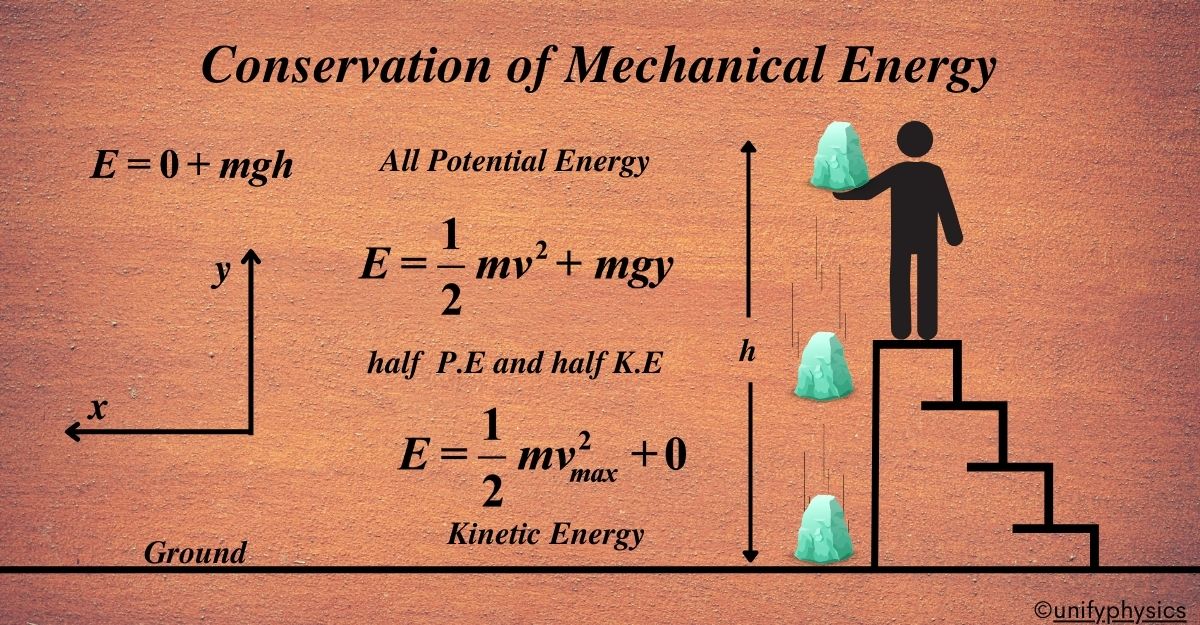
Another example is, when you drop a stone from a certain height, it possesses gravitational potential energy due to its elevated position above the ground. As the stone falls, this potential energy is converted into kinetic energy, the energy of motion. At the instant just before the stone is released, it has maximum potential energy and zero kinetic energy.

As the stone descends, its potential energy decreases while its kinetic energy increases. At some point during the fall, typically halfway between the starting point and the ground, the stone has converted half of its initial potential energy into kinetic energy. This results from the conservation of mechanical energy, which states that the total mechanical energy (the sum of potential and kinetic energy) remains constant in the absence of external forces like air resistance.

When the stone is at its lowest point, just before it hits the ground, its potential energy is at its minimum (zero), and all of its initial potential energy has been converted into kinetic energy. At this point, the stone has maximum kinetic energy, as it is moving at its maximum velocity just before impact.

The principle of conservation of mechanical energy states that in an isolated system, where only conservative forces (like gravity) are at work, the total mechanical energy remains constant. This means that the sum of potential energy and kinetic energy at any point in the system’s motion will always add up to the same total amount.

This principle is super important because it helps us predict how objects will move and interact. It’s used in designing roller coasters, calculating the orbits of planets, and even in sports science to understand how athletes perform.

Proof of Conservation of Mechanical Energy

The proof of the conservation of mechanical energy can be demonstrated through various systems, such as a pendulum or a roller coaster. In these systems, as the object moves, its potential energy is converted into kinetic energy and vice versa, but the total mechanical energy remains constant if no non-conservative forces (like friction) are doing significant work.

When you throw the ball upwards, it starts with a certain amount of kinetic energy (KE) due to its velocity. As it rises, it slows down, meaning its kinetic energy is decreasing. However, at the same time, its potential energy (PE) is increasing because it’s getting higher above the ground.

When the ball reaches its highest point, its velocity is zero, so its kinetic energy is also zero. But now, all the energy it started with is stored as potential energy.

As the ball falls back down, its potential energy decreases because it’s getting closer to the ground. But as it falls, it speeds up, so its kinetic energy increases.

The work done by all forces acting on an object equals the change in its kinetic energy.

\(\displaystyle \Delta KE = W_{total} \)

For conservative forces, like gravity, the work done is equal to the negative change in potential energy.

\(\displaystyle W_{conservative} = -\Delta PE \)

If only conservative forces are doing work, then the total work done is the change in kinetic energy, which is the negative change in potential energy.

\(\displaystyle \Delta KE = -\Delta PE \)

Adding ( \Delta PE ) to both sides gives us:

\(\displaystyle \Delta KE + \Delta PE = 0 \)

This means the change in the total mechanical energy (KE + PE) is zero, which implies that the total mechanical energy is conserved.

\(\displaystyle \Delta (KE + PE) = 0 \)

Throughout the motion of the ball, the sum of its kinetic and potential energy remains constant. This is true for any system where only conservative forces are doing work. The energy may change forms between kinetic and potential, but the total amount of mechanical energy stays the same.

Also Read: Potential Energy

Solved Examples

Example 1: A pendulum of length 2 meters swings from an initial height of 1 meter above its lowest position. Find its speed at its lowest position. Assume no air resistance.

Solution: Given;

• Length of pendulum, (l = 2) m
• Initial height, (h_i = 1) m
• Acceleration due to gravity, (g = 9.8 m/s²)

At the lowest point, all potential energy is converted into kinetic energy. So, we can use the principle of conservation of mechanical energy.

\(\displaystyle E_{\text{initial}} = E_{\text{final}} \)
\(\displaystyle mgh_i + \frac{1}{2} mv_i^2 = \frac{1}{2} mv_f^2 \)

Since the pendulum starts from rest at the highest point, (v_i = 0).

\(\displaystyle mgh_i = \frac{1}{2} mv_f^2 \)
\(\displaystyle mgh_i = \frac{1}{2} mv_f^2 \)
\(\displaystyle mg \times 1 = \frac{1}{2} m \times v_f^2 \)
\(\displaystyle 9.8 \times 1 = \frac{1}{2} \times v_f^2 \)
\(\displaystyle v_f^2 = 19.6 \)
\(\displaystyle v_f = \sqrt{19.6} \approx 4.43 \, \text{m/s} \)

Therefore, the speed of the pendulum at its lowest point is approximately (4.43 m/s).

Example 2: A 0.2 kg object is attached to a spring with a spring constant of (500 N/m). If the object is compressed by (0.1) meters and then released, find its maximum speed. Neglect air resistance.

Solution: Given;

• Mass of object, (m = 0.2) kg
• Spring constant, (k = 500 N/m)
• Compression, (x = 0.1) m

At the maximum compression, all potential energy is converted into kinetic energy. So, we can use the principle of conservation of mechanical energy.

\(\displaystyle E_{\text{initial}} = E_{\text{final}} ]
\)latex \displaystyle \frac{1}{2} kx^2 = \frac{1}{2} mv_f^2 ]

\(\displaystyle \frac{1}{2} \times 500 \times (0.1)^2 = \frac{1}{2} \times 0.2 \times v_f^2 \)
\(\displaystyle 2.5 = 0.1 \times v_f^2 \)
\(\displaystyle v_f^2 = 25 \)
\(\displaystyle v_f = 5 \, \text{m/s} \)

Therefore, the maximum speed of the object is (5 m/s).

Example 3: A roller coaster car of mass (500 kg) starts from rest at a height of (30 m) above the ground. Find its speed at a height of (20 m) above the ground. Neglect air resistance.

Solution: Given;

• Mass of car, (m = 500) kg
• Initial height, (h_i = 30) m
• Final height, (h_f = 20) m
• Acceleration due to gravity, (g = 9.8 m/s²)

Using the conservation of mechanical energy:

\(\displaystyle E_{\text{initial}} = E_{\text{final}} ]
\)latex \displaystyle mgh_i + \frac{1}{2} mv_i^2 = mgh_f + \frac{1}{2} mv_f^2 ]

Since the car starts from rest at the highest point, (v_i = 0).

\(\displaystyle mgh_i = mgh_f + \frac{1}{2} mv_f^2 \)
\(\displaystyle mgh_i – mgh_f = \frac{1}{2} mv_f^2 \)
\(\displaystyle mgh_i – mgh_f = \frac{1}{2} mv_f^2 \)
\(\displaystyle 500 \times 9.8 \times 30 – 500 \times 9.8 \times 20 = \frac{1}{2} \times 500 \times v_f^2 \)
\(\displaystyle 147000 – 98000 = 250 \times v_f^2 \)
\(\displaystyle 49000 = 250 \times v_f^2 \)
\(\displaystyle v_f^2 = \frac{49000}{250} \)
\(\displaystyle v_f^2 = 196 \)
\(\displaystyle v_f = \sqrt{196} = 14 \, \text{m/s} \)

Therefore, the speed of the car at a height of (20 m) above the ground is (14 m/s).

Example 4: A projectile is launched from the ground with an initial speed of (20 m/s) at an angle of (30^∘) above the horizontal. Find the maximum height reached by the projectile. Neglect air resistance.

Solution: Given;

• Initial speed, (v_i = 20 m/s)
• Launch angle, (θ = 30^∘)
• Acceleration due to gravity, (g = 9.8 m/s²)

At the maximum height, the projectile’s velocity is entirely vertical, so its horizontal component is (0). Using the conservation of mechanical energy, we can find the maximum height (h_max) reached by the projectile:

\(\displaystyle E_{\text{initial}} = E_{\text{final}} \)
\(\displaystyle \frac{1}{2} m v_i^2 = mgh_{\text{max}} \)

\(\displaystyle \frac{1}{2} \times 20^2 = 9.8 \times h_{\text{max}} \)
\(\displaystyle 200 = 9.8 \times h_{\text{max}} \)
\(\displaystyle h_{\text{max}} = \frac{200}{9.8} \approx 20.41 \, \text{m} \)

Therefore, the maximum height reached by the projectile is approximately (20.41 m).

Example 5: A 0.1 kg block slides down a frictionless incline of height (2 m) and lands on a spring with a spring constant of (100 N/m). Find the maximum compression of the spring. Neglect air resistance.

Solution: Given;

• Mass of block, (m = 0.1) kg
• Height of incline, (h = 2) m
• Spring constant, (k = 100 N/m)

Using the conservation of mechanical energy:

\(\displaystyle E_{\text{initial}} = E_{\text{final}} \)
\(\displaystyle mgh = \frac{1}{2} kx^2 \)

\(\displaystyle 0.1 \times 9.8 \times 2 = \frac{1}{2} \times 100 \times x^2 \)
\(\displaystyle 1.96 = 50 \times x^2 \)
\(\displaystyle x^2 = \frac{1.96}{50} \)
\(\displaystyle x = \sqrt{\frac{1.96}{50}} \)
\(\displaystyle x \approx 0.14 \, \text{m} \)

Therefore, the maximum compression of the spring is approximately (0.14 m).

Example 6: A cart of mass (2 kg) is released from a height of (5 m) on a frictionless track. At the bottom of the track, it collides elastically with another cart of mass (1 kg) initially at rest. Find the speed of each cart after the collision.

Solution: Given;

• Mass of the first cart, (m₁ = 2 kg)
• Mass of the second cart, (m₂ = 1 kg)
• Initial height, (h_i = 5 m)
• Acceleration due to gravity, (g = 9.8 m/s²)

At the bottom of the track, all potential energy is converted into kinetic energy. So, we can use the conservation of mechanical energy to find the velocity of the first cart before the collision.

\(\displaystyle E_{\text{initial}} = E_{\text{final}} \)
\(\displaystyle m_1gh_i = \frac{1}{2} m_1 v_1^2 \)

\(\displaystyle 2 \times 9.8 \times 5 = \frac{1}{2} \times 2 \times v_1^2 \)
\(\displaystyle 98 = v_1^2 \)
\(\displaystyle v_1 = \sqrt{98} = 7\sqrt{2} \approx 9.9 \, \text{m/s} \)

Since the collision is elastic, we can apply the conservation of momentum as well as the conservation of mechanical energy.

For momentum:

\(\displaystyle m_1 v_{1i} + m_2 v_{2i} = m_1 v_{1f} + m_2 v_{2f} \)
\(\displaystyle 2 \times (7\sqrt{2}) + 1 \times 0 = 2 \times v_{1f} + 1 \times v_{2f} \)
\(\displaystyle 14\sqrt{2} = 2v_{1f} + v_{2f} \)

For mechanical energy:

\(\displaystyle \frac{1}{2} m_1 v_{1i}^2 = \frac{1}{2} m_1 v_{1f}^2 + \frac{1}{2} m_2 v_{2f}^2 \)
\(\displaystyle \frac{1}{2} \times 2 \times (7\sqrt{2})^2 = \frac{1}{2} \times 2 \times v_{1f}^2 + \frac{1}{2} \times 1 \times v_{2f}^2 \)
\(\displaystyle 98 = 2v_{1f}^2 + \frac{1}{2}v_{2f}^2 \)

Now, we have a system of two equations:

\(\displaystyle 14\sqrt{2} = 2v_{1f} + v_{2f} \) (1)
\(\displaystyle 98 = 2v_{1f}^2 + \frac{1}{2}v_{2f}^2 \) (2)

Let’s solve this system of equations.

From equation (1):

\(\displaystyle v_{2f} = 14\sqrt{2} – 2v_{1f} \) (3)

Substitute equation (3) into equation (2):

\(\displaystyle 98 = 2v_{1f}^2 + \frac{1}{2}(14\sqrt{2} – 2v_{1f})^2 \)

Solve for (v_1f):

\(\displaystyle 98 = 2v_{1f}^2 + \frac{1}{2}(196 – 56\sqrt{2}v_{1f} + 4v_{1f}^2) \)
\(\displaystyle 98 = 2v_{1f}^2 + 98 – 28\sqrt{2}v_{1f} + 2v_{1f}^2 \)
\(\displaystyle 0 = 4v_{1f}^2 – 28\sqrt{2}v_{1f} \)
\(\displaystyle 0 = v_{1f}(v_{1f} – 7\sqrt{2}) \)

So, (v_1f = 0) or \(\displaystyle v_{1f}= 7\sqrt{2}\).

Since \(\displaystyle v_{1f} \neq 0\), we have:

\(\displaystyle v_{2f} = 14\sqrt{2} – 2(7\sqrt{2}) = 0 \)

Therefore, after the collision, the first cart moves with a velocity of \(\displaystyle 7\sqrt{2} \, \text{m/s}\) to the right, and the second cart comes to rest.

FAQs