The story of current electricity is not just about circuits and wires; it’s a tale of human curiosity and ingenuity. It begins with the ancient Greeks, like Thales of Miletus, who discovered static electricity over 2,500 years ago by rubbing amber with fur. However, it wasn’t until the 18th century that scientists like Luigi Galvani and Alessandro Volta began to understand and harness electricity in ways that could power devices.
Fast forward to the late 19th century, a pivotal period known as the War of the Currents. This was a time of intense rivalry between Thomas Edison, Nikola Tesla, and George Westinghouse. Edison, the inventor of the practical light bulb, was a staunch supporter of direct current (DC), which flows steadily in one direction. He even built the first power plant in New York City in 1882 to distribute DC electricity.
Tesla, a brilliant engineer from Croatia, immigrated to America and initially worked for Edison. He improved Edison’s DC generators but also had his own invention: an alternating current (AC) motor. Edison dismissed AC, but Tesla didn’t give up. He eventually sold his patents to Westinghouse, and together they championed AC, which could be transmitted over long distances more economically than DC.
The real turning point came when Westinghouse won the contract to light up the 1893 World’s Fair in Chicago with Tesla’s AC system. It was a dazzling showcase that proved AC’s superiority. Following this, Westinghouse built the first major hydroelectric power plant at Niagara Falls, which successfully transmitted electricity to Buffalo, New York, 26 miles away.
The battle ended with AC becoming the dominant form of electricity transmission around the world. Today, we use both AC and DC for different applications, but it’s the AC from our wall outlets that powers most of our homes and offices.
What Is Current Electricity?
Current electricity is the flow of electric charge through a conductor. This flow is typically carried by moving electrons in a wire. It’s used to power everything from household appliances to complex machinery.
Imagine a river flowing smoothly through a landscape; this is similar to how current electricity works. It’s the steady, controlled flow of electric charge through a material, usually a wire, that powers our devices and appliances.

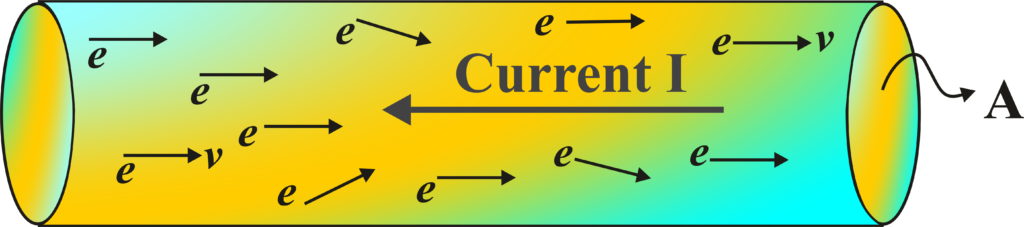
In technical terms, current electricity is defined as the flow of electrons from one section of the circuit to another. These electrons move because they are attracted to the positive side of a power source and repelled by the negative side, creating a flow of charge.
Electrons are tiny particles that carry a negative charge. In a conductor, like a copper wire, these electrons are free to move. When we connect a wire to a battery or a power source, we create a difference in electric potential (voltage) between the ends of the wire. This difference pushes the electrons to flow from the negative side (where there are more electrons) to the positive side (where there are fewer electrons).
Voltage, or electromotive force (EMF), is the “push” that drives electrons through a conductor. It’s like the pressure that pushes water through a pipe. Without voltage, there would be no flow of current, just as without water pressure, there would be no flow of water.
We measure current in units called amperes (amps), which tell us how many electrons are passing through a conductor at any given time. One ampere is equal to one coulomb of charge passing through a point in one second.
Current electricity is essential because it’s the form of electricity that we can control and use to power all sorts of devices, from the smallest smartphone to the largest supercomputer. It’s a fundamental concept in physics and is the backbone of modern technology.
What is Drift Velocity?
Drift velocity is the average velocity that a particle, such as an electron, attains due to an electric field. In simple terms, it’s how fast electrons are “drifting” through a material. Imagine you’re in a large field with a group of friends, and you’re all spread out. If you start walking towards a common point, your movement towards that point is similar to drift velocity.
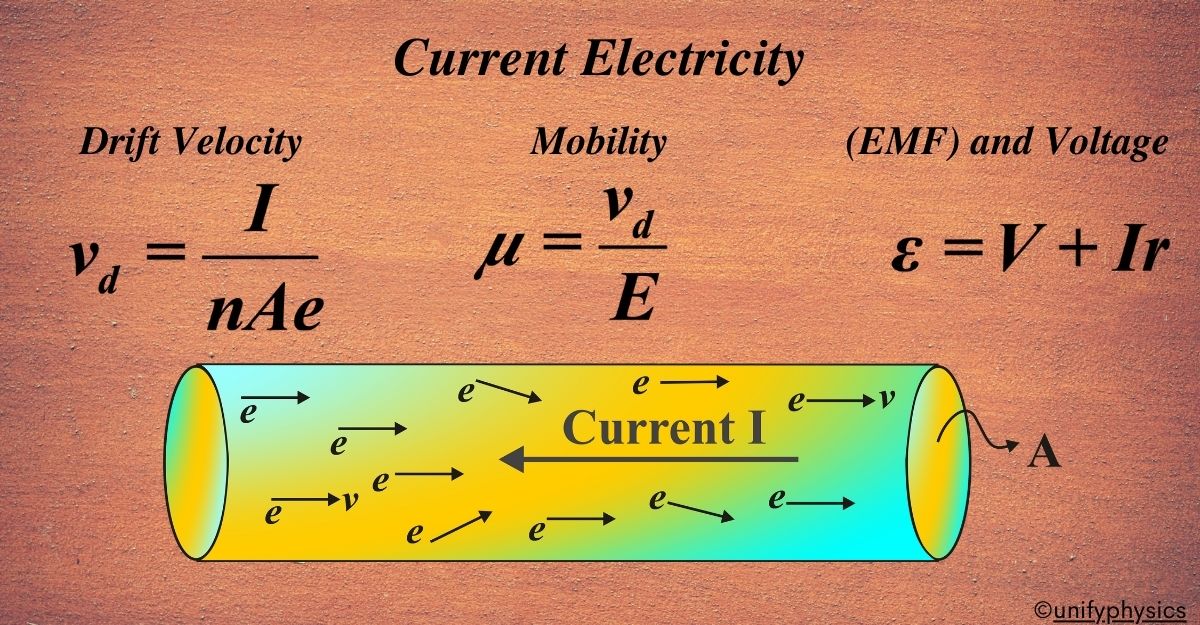
In physics, when we talk about drift velocity (vd), we’re referring to the average velocity that charged particles, like electrons, attain due to an electric field in a conductor. It’s not the random, high-speed movement that electrons have because of their temperature; it’s a slow, steady movement in one direction.
The formula to calculate drift velocity is:
\(\displaystyle v_d = \frac{I}{nAe} \)
- (I) is the current flowing through the conductor,
- (n) is the number of charge carriers per unit volume,
- (A) is the cross-sectional area of the conductor,
- (e) is the charge of an electron.
When an electric field is applied to a conductor, electrons start to “drift” towards the positive end. This drift is superimposed on their random thermal motion. The drift velocity represents the average velocity with which the free electrons move toward the positive end.
Drift velocity is crucial because it directly relates to the electric current flowing through a conductor. It helps us understand how materials respond to electric fields and is a fundamental concept in designing electronic circuits.
Mobility
Mobility is a measure of how quickly and easily electrons or other charge carriers can move through a material when an electric field is applied. It’s like measuring how fast you can walk on different surfaces; walking on a smooth sidewalk is easier (higher mobility) than walking through a sandy beach (lower mobility).
Mobility (µ) is defined by the equation:
\(\displaystyle \mu = \frac{v_d}{E} \)
where (vd) is the drift velocity, and (E) is the electric field strength. This tells us that mobility is the drift velocity of charge carriers per unit of electric field strength.
Mobility is important because it affects how well a material conducts electricity. High mobility means charge carriers can move more freely, making the material a better conductor. This is crucial in devices like transistors and semiconductors, where we need electrons to move quickly.
Factors Affecting Mobility: Several factors can affect mobility, including:
- Temperature: Higher temperatures can increase the energy of charge carriers, potentially increasing mobility.
- Material Type: Different materials have different levels of mobility. For example, metals typically have higher mobility than semiconductors.
- Impurities: Adding impurities to a material can either increase or decrease mobility, depending on the type of impurity and the material.
In practical terms, when you increase the electric field across a material, the charge carriers move faster, and the current increases. This is why mobility is a key parameter in designing electronic circuits—it helps us predict how the circuit will behave under different conditions.
Relation Between Mobility And Electric Current
First, recall that mobility (µ) is how quickly charge carriers (like electrons) can move through a material when an electric field is applied. It’s a bit like measuring how fast you can run in different environments; running on a track is easier (higher mobility) than running in a pool (lower mobility).
Mobility is given by the equation:
\(\displaystyle \mu = \frac{v_d}{E} \)
where (vd) is the drift velocity, and (E) is the electric field strength. Now, let’s connect mobility to electric current (I). Remember, electric current is the flow of charge through a conductor, and it’s measured in amperes (A). The formula for current, considering drift velocity, is:
\(\displaystyle I = nAev_d \)
- (n) is the number of charge carriers per unit volume,
- (A) is the cross-sectional area of the conductor,
- (e) is the charge of an electron,
- (vd) is the drift velocity.
To find the relationship between mobility and electric current, we can combine the two formulas. Since (vd = µE ), we can substitute (vd) in the current formula to get:
\(\displaystyle I = nAe(\mu E) \)
This shows that the electric current is directly proportional to the mobility of the charge carriers. Higher mobility means charge carriers can move more freely, leading to a higher current for a given electric field strength.
In practical terms, materials with higher mobility are preferred for electrical and electronic applications because they allow for more efficient current flow. This is why materials like copper and silver, which have high mobility, are commonly used in wires and other electrical components.
Current Density
Current density (J) is the electric current per unit area of cross-section. Imagine you’re at a concert, and the crowd is the electric charge. The area near the stage is a particular section of the conductor. Now, current density tells us how tightly packed the crowd is in that area. It’s a measure of how much electric charge is flowing through a specific area of the conductor in a given amount of time.
Current density is a vector quantity that describes the amount of electric current flowing through a unit cross-sectional area perpendicular to the flow of the current within a conducting material. It gives us insight into the distribution and concentration of electric current at different points in the conductor.
The formula for current density (J) is:
\(\displaystyle J = \frac{I}{A} \)
- (I) is the electric current flowing through the conductor (measured in Amperes),
- (A) is the cross-sectional area of the conductor (measured in square meters).
Current density is important because it helps us understand how the electric current is distributed across a conductor. In some areas, the current may be more concentrated, and in others, less so. This can affect how a material performs and is particularly important in the design of electrical components and circuits.
Think of a highway with multiple lanes. The cars represent the electric current, and the lanes represent different areas in the conductor. Some lanes might have more cars (higher current density), while others have fewer (lower current density). Current density helps us quantify this distribution of cars (electric current) in each lane (point in the conductor).
Flow of Current through Conductor
The flow of current through a conductor follows Ohm’s Law, which states that the current (I) through a conductor between two points is directly proportional to the voltage (V) across the two points.
Think of a conductor as a highway for electrons. When the highway is clear (meaning there’s a potential difference or voltage across the conductor), the electrons can ‘drive’ from one end to the other. This movement of electrons is what we call electric current.
In conductors, such as metals, there are lots of free electrons that are not bound to any particular atom. These free electrons can move more easily when an electric field (created by a voltage) is applied.
When you connect a conductor to a battery, the negative terminal pushes electrons away (since they’re negatively charged), and the positive terminal attracts them. This creates a flow of electrons, which we observe as an electric current.
The flow of current through a conductor is described by Ohm’s Law. It states that the current (I) is directly proportional to the voltage (V) and inversely proportional to the resistance (R) of the conductor. The formula is:
\(\displaystyle I = \frac{V}{R} \)
This means if you increase the voltage, the current will increase, provided the resistance stays the same. Conversely, if you increase the resistance, the current will decrease for the same voltag.
Resistance is a measure of how much a conductor resists the flow of current. It depends on the material’s properties, the cross-sectional area, and the length of the conductor. Conductivity is the inverse of resistance and tells us how well a material can carry an electric current.
Generation of Electric Current
Electric current can be generated by moving a conductor in a magnetic field, chemical reactions in batteries, or through photovoltaic cells. The generation of electric current is like creating a flow of water in a river. Just as water needs a slope to flow, electric charges need a push to move. This push is provided by various methods that we’ll explore.
Methods of Generating Electric Current
1) By Moving a Conductor in a Magnetic Field: Imagine moving a wire through a magnetic field. This movement creates a change in the magnetic environment around the wire, which, according to Faraday’s Law of Electromagnetic Induction, induces an electric current in the wire. This method can generate both alternating current (AC) and direct current (DC), depending on the design of the generator.
2) By Chemical Reactions in a Battery: In a battery, chemical reactions occur that transfer electrons from one material to another. This transfer creates a potential difference between the battery terminals and, when connected in a circuit, causes an electric current to flow. Batteries typically generate direct current (DC), which flows in one direction.
3) By Photovoltaic Effect: Solar panels use the photovoltaic effect to generate electric current. When sunlight hits the panel, it excites electrons, creating a flow of electric charge.
Understanding how electric current is generated is crucial for harnessing energy to power our homes, devices, and industries.
Electromotive Force (EMF) and Voltage
Electromotive Force (EMF) is the energy provided by a source like a battery or generator per unit charge. It’s the “pressure” that pushes the charges through the circuit. Voltage is the potential difference between two points in a circuit. It’s what drives the current from one point to another.
Electromotive Force (EMF): Electromotive Force (EMF) is the energy source that creates the potential difference in an electrical circuit. It’s like the pump in a water system that creates pressure to move water through the pipes. In electrical terms, EMF is the energy supplied by a battery or generator that pushes electrons through a circuit.
Voltage: Voltage: is the measure of the potential difference between two points in a circuit. It’s similar to the pressure difference in a water system that determines how much water flows from one point to another. In simpler terms, voltage is what you measure when you use a voltmeter across a battery’s terminals.
While EMF is the total energy supplied to move a charge through the entire circuit, voltage is the energy difference that moves the charge between two specific points in the circuit. You can think of EMF as the cause and voltage as the effect.
The relationship between EMF (ε), voltage (V), current (I), and internal resistance (r) of a cell can be expressed as:
\(\displaystyle \varepsilon = V + Ir \)
This equation tells us that the EMF is equal to the terminal voltage plus the product of the current and the internal resistance of the cell².
When you plug in a device, the voltage across the power source provides the “push” needed to drive the current through the device. The EMF is the reason this voltage exists in the first place, originating from the chemical reactions in a battery or the mechanical energy in a generator.
Types of Current Electricity
There are two main types of current:
Direct Current (DC)
Direct Current is the unidirectional flow of electric charge. Batteries provide DC. Direct Current (DC) is a type of electric current that flows in only one direction through a conductor, like a wire. Imagine a river flowing steadily in one direction; that’s how DC moves through circuits³.
Unlike water in the ocean that moves back and forth with the tides, DC electricity flows in one constant direction. DC provides a constant voltage, which means the power it delivers doesn’t change with time.
Your everyday AA or AAA batteries provide DC, which is why they have a positive (+) and a negative (-) terminal. When sunlight hits solar panels, they generate DC, which can be used to power devices or charge batteries. These convert chemical energy into electrical energy, providing DC for various applications.
Most of our gadgets, like smartphones and laptops, run on DC. That’s why we need adapters to convert the AC from our outlets into DC. Cars that run on electricity use DC motors powered by large battery packs.
In circuit diagrams, DC is often represented by a straight line with a dashed line underneath it. This symbol indicates the steady, unchanging nature of DC. DC is crucial for its stability and reliability in powering many of our daily-use electronic devices. It’s also important in applications where varying power levels could be harmful or less effective.
Alternating Current (AC)
Alternating Current changes direction periodically. The electricity supplied to homes is AC. Alternating Current (AC) is like the ocean’s tides, constantly changing direction and strength. In AC, the electric current changes its direction and magnitude periodically. It’s the type of current that powers our homes and schools.
AC and voltage rise and fall in a sinusoidal pattern, meaning they follow a wave-like motion over time. This is the number of times the current changes direction per second, measured in hertz (Hz). In most countries, the frequency of AC is either 50 Hz or 60 Hz.
The instantaneous value of AC can be expressed mathematically as:
\(\displaystyle I = I_0 \sin(\omega t) \)
- (I) is the instantaneous current,
- (I0) is the peak value of the current,
- (ω) is the angular frequency,
- (t) is the time.
AC is used for distributing power over long distances because it can easily be transformed to different voltages with transformers. Most household appliances are designed to run on AC because it’s the standard form of electrical output from power plants.
While Direct Current (DC) is like a river that flows steadily in one direction, AC is like the sea waves, moving back and forth. This fundamental difference makes AC ideal for the power grid and DC ideal for battery-powered devices.
If you were to look at AC on a graph, you’d see a wave that rises and falls smoothly. This wave represents how the current and voltage increase to a peak, decrease back to zero, and then reverse and repeat the process.
Current Electricity vs Static Electricity
Current electricity involves a continuous flow of charge, while static electricity is where charge accumulates on an object’s surface.
| Parameter | Current Electricity | Static Electricity |
|---|---|---|
| Definition | The flow of electric charge through a conductor, typically in a steady stream of electrons. | This occurs in conductors where charges can move freely. |
| Nature | Dynamic, with electrons in constant motion. | Stationary, with charges building up in one place. |
| Duration | Can last as long as there’s a power source. | Exists momentarily until discharged. |
| Cause | Caused by a potential difference (voltage) across a conductor. | Often caused by friction between two different materials. |
| Conductivity | Occurs in conductors where charges can move freely. | Can occur in both conductors and insulators. |
| Magnetic Field | Generates a magnetic field due to moving charges. | Does not typically generate a magnetic field. |
| Measurement | Measured in amperes (current) using meters. | Measured using devices like the gold leaf electroscope. |
| Examples | Running appliances, powering lights, and electronic devices. | Lightning, static cling, and shocks from touching a metal object. |
Heating Effect of Current
When current flows through a conductor, it generates heat due to the resistance. This is known as the Joule heating effect, and it’s the principle behind devices like electric heaters.
When electric current flows through a conductor, like a wire, it doesn’t just travel silently; it brings a warm change. This is the heating effect of current, and it’s something you’ve experienced if you’ve ever noticed a charger getting warm while using it.
- Free Electrons in Motion: In a conductor, free electrons move and collide with atoms. These collisions cause resistance and make the electrons lose some of their kinetic energy.
- Energy Transformation: The lost kinetic energy transforms into heat energy, warming up the conductor.
The heating effect of current is quantified by Joule’s Law of Heating, which states:
\(\displaystyle H = I^2Rt \)
- (H) is the heat energy produced in joules,
- (I) is the current in amperes,
- (R) is the resistance in ohms,
- (t) is the time in seconds that the current flows.
Examples: The filament in a bulb heats up due to the current, producing light. They use the heating effect to warm up spaces. Designed to melt and break the circuit if too much current flows, preventing damage.
The heating effect of current is crucial for designing safe electrical systems. It helps us choose the right materials and create devices that use the heat produced, like toasters or hair dryers.
Also Read: Energy Stored In Capacitors
Relative Motion Between Magnetic Field and Coil
Imagine you have a magnet and a coil of wire. When they’re both still, nothing much happens. But when you move the magnet towards the coil or the coil towards the magnet, something incredible occurs: electricity is generated! This is due to a phenomenon called electromagnetic induction.
Electromagnetic induction is the process by which a changing magnetic field within a coil of wire induces an electromotive force (EMF), leading to the generation of electric current if the circuit is closed.
- Magnetic Flux: Think of magnetic flux as the number of magnetic lines of force passing through the coil. It’s like the amount of water flowing through a pipe.
- Changing Flux: When there’s relative motion between the magnet and the coil, the amount of magnetic flux through the coil changes.
- Induced EMF: This change in flux induces an EMF in the coil. It’s like the pressure difference that causes water to flow.
The amount of induced EMF is directly proportional to the rate of change of magnetic flux through the coil. This is described by Faraday’s Law of Electromagnetic Induction, which can be mathematically expressed as:
\(\displaystyle \varepsilon = -N \frac{\Delta \phi}{\Delta t} \)
- ( \(\displaystyle \varepsilon \)) is the induced EMF,
- (N) is the number of turns in the coil,
- (\(\displaystyle \Delta \phi\) ) is the change in magnetic flux,
- ( \(\displaystyle\Delta t \)) is the change in time.
Lenz’s Law tells us about the direction of the induced current. It states that the induced current will flow in such a way that it opposes the change in flux that produced it.
In power plants, turbines move coils within magnetic fields to generate electricity. When you play a string, it moves within the magnetic field of the pickup coil, inducing an EMF.
Solved Examples
Problem 1: A copper wire with a cross-sectional area of (1 mm2) carries a current of (3 A). Calculate the drift velocity of electrons in the wire. Assume the number density of conduction electrons in copper is (\(\displaystyle 8.5 \times 10^{28} \, \text{m}^{-3}\)).
Solution: The drift velocity (vd) is given by:
\(\displaystyle v_d = \frac{I}{n e A} \)
Calculate (vd):
\(\displaystyle v_d = \frac{3}{8.5 \times 10^{28} \times 1.6 \times 10^{-19} \times 1 \times 10^{-6}}\)
\(\displaystyle v_d = \frac{3}{1.36 \times 10^{4}} \)
\(\displaystyle v_d \approx 2.21 \times 10^{-4} \, \text{m/s} \)
Therefore, the drift velocity of electrons in the wire is approximately (\(\displaystyle 2.21 \times 10^{-4} \, \text{m/s} \)).
Problem 2: If the drift velocity of electrons in a conductor is (\(\displaystyle 1.5 \times 10^{-4} \, \text{m/s} \)) under the influence of an electric field of (10 V/m), calculate the mobility of the electrons.
Solution: The mobility (µ) is given by:
\(\displaystyle \mu = \frac{v_d}{E} \)
Calculate (µ):
\(\displaystyle \mu = \frac{1.5 \times 10^{-4}}{10} \)
\(\displaystyle \mu = 1.5 \times 10^{-5} \, \text{m}^2/\text{V} \cdot \text{s} \)
Therefore, the mobility of the electrons is ( 1.5 \times 10^{-5} \, \text{m}^2/\text{V} \cdot \text{s} ).
Problem 3: Calculate the current flowing through a copper wire of length (2 m) and cross-sectional area ( \(\displaystyle 0.5 \, \text{mm}^2 \)), given that the mobility of electrons is (\(\displaystyle 4.5 \times 10^{-3} \, \text{m}^2/\text{V} \cdot \text{s} \)) and the electric field applied is (\(\displaystyle 20 \, \text{V/m} \)).
Solution: First, find the drift velocity:
\(\displaystyle v_d = \mu E \)
\(\displaystyle v_d = 4.5 \times 10^{-3} \times 20 \)
\(\displaystyle v_d = 9 \times 10^{-2} \, \text{m/s} \)
The current (I) is given by:
\(\displaystyle I = n e A v_d \)
Calculate ( I ):
\(\displaystyle I = 8.5 \times 10^{28} \times 1.6 \times 10^{-19} \times 0.5 \times 10^{-6} \times 9 \times 10^{-2} \)
\(\displaystyle I = 8.5 \times 1.6 \times 0.5 \times 9 \times 10^{1} \)
\(\displaystyle I \approx 6.12 \, \text{A}\)
Therefore, the current flowing through the wire is approximately ( 6.12A).
Problem 4: Calculate the heat produced in a resistor of (5 Ω) when a current of (2 A) flows through it for ( 10 s).
Solution: The heat produced (H) is given by:
\(\displaystyle H = I^2 R t \)
Calculate (H):
\(\displaystyle H = (2)^2 \times 5 \times 10 \)
\(\displaystyle H = 4 \times 5 \times 10\)
\(\displaystyle H = 200 \, \text{J} \)
Therefore, the heat produced in the resistor is ( 200 J ).
Problem 5: A conductor of length ( 50 cm) and cross-sectional area ( 1 cm2 ) has a resistance of ( 0.02 ω). If a potential difference of (1 V) is applied across it, calculate the current flowing through the conductor.
Solution: The current (I) is given by Ohm’s Law:
\(\displaystyle I = \frac{V}{R}\)
Calculate (I):
\(\displaystyle I = \frac{1}{0.02} \)
\(\displaystyle I = 50 \, \text{A} \)
Therefore, the current flowing through the conductor is ( 0 A).
Problem 6: A coil of ( 100 ) turns and area ( 0.1 m2 ) is placed in a magnetic field of ( 0.2 T. If the coil is rotated at ( 50 rpm} ) perpendicular to the magnetic field, calculate the induced emf.
Solution: The induced emf ( \(\displaystyle \epsilon \)) in a rotating coil is given by:
\(\displaystyle \epsilon = NAB \omega \sin(\omega t) \)
The maximum emf occurs when ( \(\displaystyle \sin(\omega t) = 1 \)), so:
\(\displaystyle \epsilon_{\text{max}} = NAB \omega\)
Calculate ( \(\displaystyle \epsilon_{\text{max}}\) ):
\(\displaystyle \epsilon_{\text{max}} = 100 \times 0.1 \times 0.2 \times 5.24\)
\(\displaystyle \epsilon_{\text{max}} = 10 \times 0.2 \times 5.24\)
\(\displaystyle \epsilon_{\text{max}} = 10.48 \, \text{V}\)
Therefore, the maximum induced emf in the coil is ( 10.48 V).
FAQs
What is current electricity and how is it different from static electricity?
Current electricity refers to the flow of electric charge through a conductor, typically driven by a voltage difference. Unlike static electricity, which involves the accumulation of charge in one place, current electricity involves the continuous movement of charge carriers, such as electrons, through a material.
What is drift velocity in the context of current electricity?
Drift velocity is the average velocity of charge carriers, such as electrons, as they move through a conductor under the influence of an electric field. It is much slower than the speed of the electric field itself and is responsible for the flow of electric current.
What is mobility in terms of charge carriers in a conductor?
Mobility is a measure of how quickly charge carriers, like electrons or holes, can move through a material when subjected to an electric field. It depends on the properties of the material and the type of charge carriers present.
How is mobility related to electric current?
Mobility is directly related to electric current because higher mobility means charge carriers can move more freely through the conductor, resulting in a higher current for a given electric field. This relationship helps determine the conductivity of a material.
How does the flow of current through a conductor occur?
The flow of current through a conductor occurs when an electric field is applied, causing free electrons in the conductor to move in a direction opposite to the field. This movement of electrons constitutes the electric current, which flows from the negative terminal to the positive terminal.
What is the heating effect of current in a conductor?
The heating effect of current, also known as Joule heating, occurs when an electric current passes through a conductor, causing it to heat up. This happens due to the collisions between moving electrons and the atoms of the conductor, which transfer energy to the atoms and increase their thermal energy.
How is the heating effect of current utilized in practical applications?
The heating effect of current is utilized in various practical applications, such as in electric heaters, toasters, and incandescent light bulbs. In these devices, the resistance of the conductor is designed to convert electrical energy into heat efficiently, providing warmth or light as needed.