Diffraction of Light

The story of diffraction begins in the 17th century with an Italian scientist named Francesco Maria Grimaldi. He was the first to document the phenomenon of diffraction in detail. In his work “Physico-Mathesis de Lumine, Coloribus, et Iride” (Physical-Mathematical Treatise on Light, Colors, and the Rainbow), published posthumously in 1665, Grimaldi described how light bends around obstacles and spreads into regions of shadow—an effect he named “diffraction,” derived from the Latin ‘diffringere,’ meaning ‘to break into pieces’.

The next significant advancement came from the Dutch scientist Christiaan Huygens. In 1678, he proposed the wave theory of light to explain the straight-line propagation of light and its ability to bend around corners. Huygens’ principle states that every point on a wavefront is itself the source of spherical wavelets, and the wavefront is the envelope of these wavelets. This principle laid the groundwork for understanding diffraction, reflection, and refraction of light waves.

The nature of light was hotly debated in the centuries that followed. Sir Isaac Newton, influenced by Grimaldi’s work, believed light was composed of particles, called ‘corpuscles.’ This view dominated for a while, but it couldn’t satisfactorily explain phenomena like interference and diffraction.

Enter Thomas Young, an English polymath who, in the early 19th century, performed the famous double-slit experiment. This experiment demonstrated that light could produce interference patterns, a behavior that only waves could exhibit. Young’s work provided strong evidence for the wave theory of light and helped explain the diffraction patterns observed by Grimaldi.

The French engineer Augustin-Jean Fresnel and the German physicist Joseph von Fraunhofer independently provided mathematical descriptions of diffraction. Fresnel’s work focused on near-field diffraction (now known as Fresnel diffraction), while Fraunhofer dealt with far-field diffraction (Fraunhofer diffraction). Their equations and models are still used today to predict and analyze diffraction patterns in various optical setups.

In the 20th century, the concept of diffraction took a quantum leap with the development of quantum mechanics. Scientists like Louis de Broglie proposed that particles such as electrons have wave-like properties, leading to the discovery of electron diffraction. This wave-particle duality further enriched the understanding of diffraction and bridged the gap between classical and quantum physics.

What is Diffraction?

Diffraction of light is the bending of light waves around the edges of an obstacle or aperture that has a size comparable to the wavelength of light. This results in the light spreading out and producing patterns of light and dark bands.

Imagine you’re at a water park, and there’s a big wall with a small gap in it. You notice that when waves hit the gap, they don’t just go straight through; they start to spread out in a semicircle on the other side. This spreading out of waves after they pass through a small opening or go around an obstacle is similar to what happens with light in diffraction.

In physics, diffraction refers to the bending and spreading of waves, especially light and sound waves, when they encounter an obstacle or a slit that is comparable in size to their wavelength. It’s like the waves are hugging the corners of the obstacle or squeezing through the slit and fanning out as a result.

When light encounters such an obstacle or slit, it doesn’t just stop or go straight; it bends around the edges and creates a pattern of spreading and overlapping waves. This pattern can be seen as a series of bright and dark bands on a screen placed behind the obstacle, which is the result of the waves interfering with each other—some reinforcing each other to make bright spots (constructive interference) and some canceling each other out to make dark spots (destructive interference).

The key thing to remember is that diffraction is all about the interaction between waves and obstacles. The size of the obstacle or slit relative to the wavelength of the light is what determines how much the light will spread out. If the opening is much larger than the light’s wavelength, there won’t be much diffraction; the waves will mostly go straight through. But if the opening is about the same size as the wavelength, the diffraction effects become very noticeable.

This phenomenon is not just limited to light; it can happen with any type of wave, including sound waves, water waves, and even waves associated with particles like electrons (thanks to the wave-particle duality in quantum mechanics).

Types of Diffraction

When we talk about diffraction, we’re essentially discussing how light waves can bend around obstacles or spread out after passing through small openings. However, not all diffraction is the same; it can be categorized based on the conditions under which it occurs. There are two primary types of diffraction that you should know about Fresnel Diffraction and Fraunhofer Diffraction.

Fresnel Diffraction

Named after the French physicist Augustin-Jean Fresnel, this type of diffraction occurs when either the light source or the observation screen (or both) is at a finite distance from the diffracting object. In Fresnel diffraction, the light waves emanate from the source and spread out as they travel, forming a pattern that changes in size and intensity as you move the screen closer to or farther from the slit.

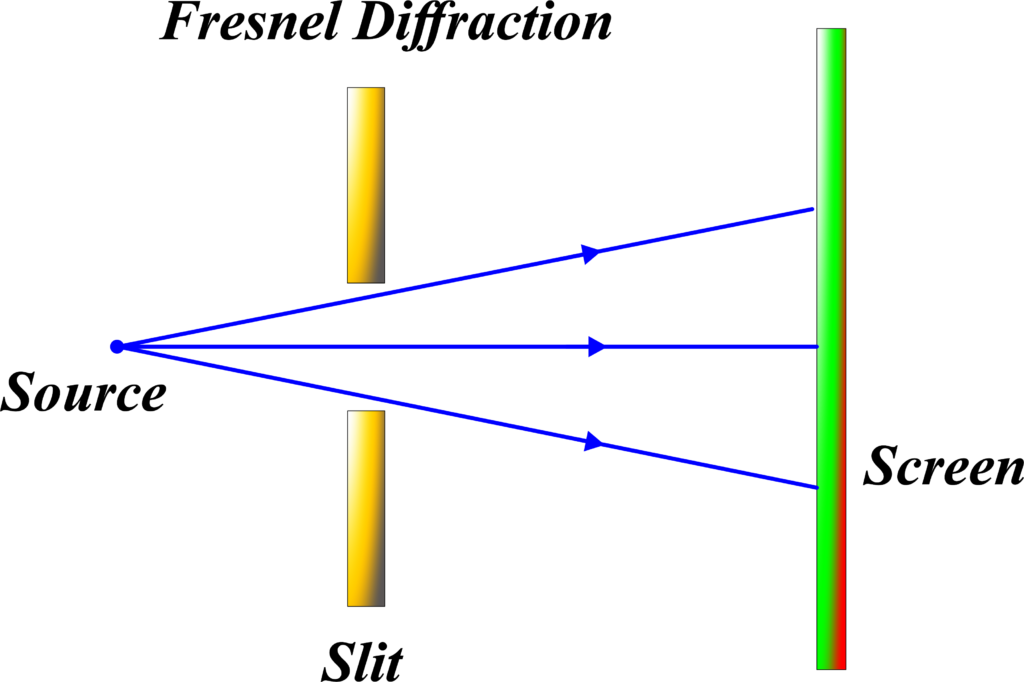
Think of it like this: if you’re holding a flashlight close to a wall with a small hole, the pattern you’ll see on another wall behind the hole will change as you move the flashlight or the second wall. The light waves are essentially ‘hugging’ the edges of the hole and interfering with each other in complex ways, creating a pattern that’s unique to the specific distances involved.

Characteristics of Fresnel Diffraction:

• Complex Patterns: The diffraction patterns produced in Fresnel Diffraction are more complex and change with the distance between the source, the aperture, and the observation screen.
• Near-Field Diffraction: It’s also known as near-field diffraction because it deals with the behavior of waves in the vicinity of the aperture.
• Zone Plates: Fresnel also introduced the concept of zone plates, which are used to focus light in Fresnel diffraction setups. These plates have concentric rings that are alternately opaque and transparent, allowing certain parts of the diffracted wave to interfere constructively.

In Fresnel Diffraction, the wavefront at any point beyond the aperture is constructed by considering each point on the aperture as a source of secondary wavelets (as per Huygens’ Principle). The intensity at any point is found by adding the contributions from each of these wavelets, taking into account their phases.

While Fresnel Diffraction is more complex to analyze mathematically due to the variable distances involved, it’s very important in understanding how light behaves in practical situations, such as in the design of optical instruments and understanding the behavior of light in everyday scenarios.

So, Fresnel Diffraction is a fascinating phenomenon that occurs when light interacts with objects in the near field, producing intricate patterns that change with the relative positions of the light source, the object, and the screen. It’s a testament to the wave nature of light and provides a deeper insight into the behavior of waves.

Fraunhofer Diffraction

Fraunhofer Diffraction is named after the German physicist Joseph von Fraunhofer. This type of diffraction is observed when the light source and the observation screen are both effectively at infinite distances from the diffracting object. This is a simplified model because, in practice, we can’t have an infinite distance. However, we can simulate this condition by using lenses to focus the light into parallel rays before and after it passes through the slit.

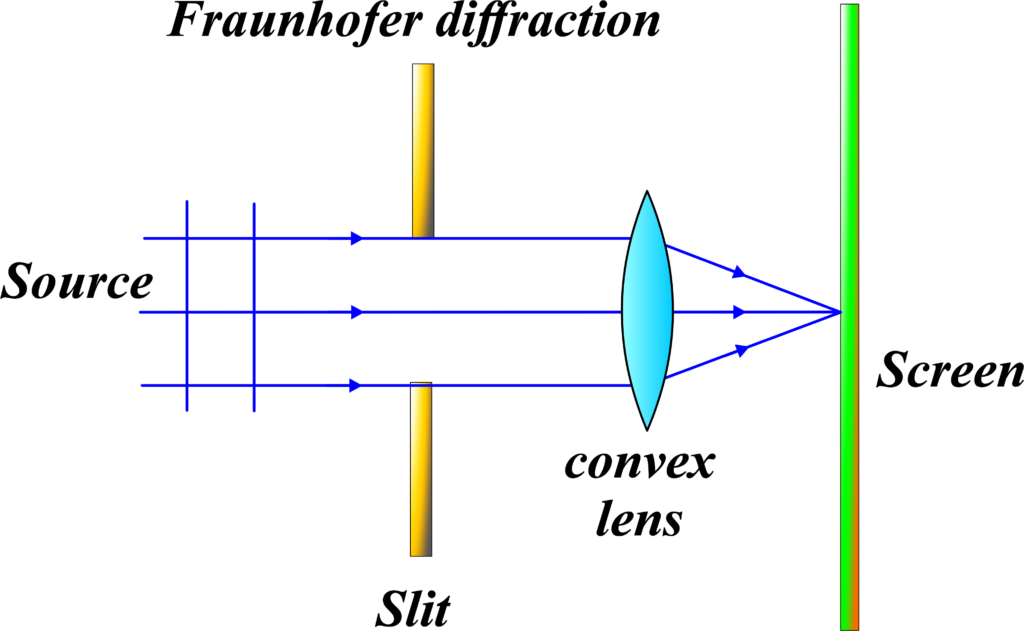
In Fraunhofer diffraction, the light waves are parallel when they hit the diffracting object and when they reach the observation screen. This results in a more straightforward and predictable diffraction pattern. It’s like if you had a very distant light source (like a star) shining through a hole, the pattern on a screen far away would stay the same, no matter how you move the screen.

Imagine you’re looking at a distant streetlight through a narrow slit in a fence. The light from the streetlight is coming from so far away that by the time it reaches the slit, the light waves are moving in parallel lines. This is similar to the conditions required for Fraunhofer Diffraction.

Characteristics of Fraunhofer Diffraction:

• Parallel Light Waves: The light waves are parallel when they hit the aperture and when they form the diffraction pattern.
• Simplified Analysis: Because the waves are parallel, the math behind Fraunhofer Diffraction is less complex than that of Fresnel Diffraction.
• Predictable Patterns: The diffraction patterns are more predictable and easier to analyze, making Fraunhofer Diffraction a preferred model for studying diffraction in laboratories.

In Fraunhofer Diffraction, the intensity of the light at any point on the screen can be calculated using a relatively simple formula because the wavefronts are considered flat (plane wavefronts). The condition for the minima (dark fringes) in the diffraction pattern is given by:

\(\displaystyle d \sin(\theta) = m\lambda \)

where (d) is the distance between the slits (in the case of a double slit), (θ) is the angle at which the fringe is observed, (m) is an integer representing the order of the minimum, and (λ) is the wavelength of light.

A common example of Fraunhofer Diffraction is the pattern created by a laser beam passing through a pair of slits and projecting onto a distant screen. The resulting pattern of bright and dark fringes is a classic demonstration of this phenomenon.

Fraunhofer Diffraction is a model that simplifies the study of diffraction by considering the light source and the screen to be at ‘infinite’ distances from the aperture. This allows for a clearer understanding of how light behaves when it encounters small openings, and it’s a fundamental concept in the field of wave optics.

The key difference between Fresnel and Fraunhofer diffraction lies in the relative distances of the light source and the screen from the diffracting object.

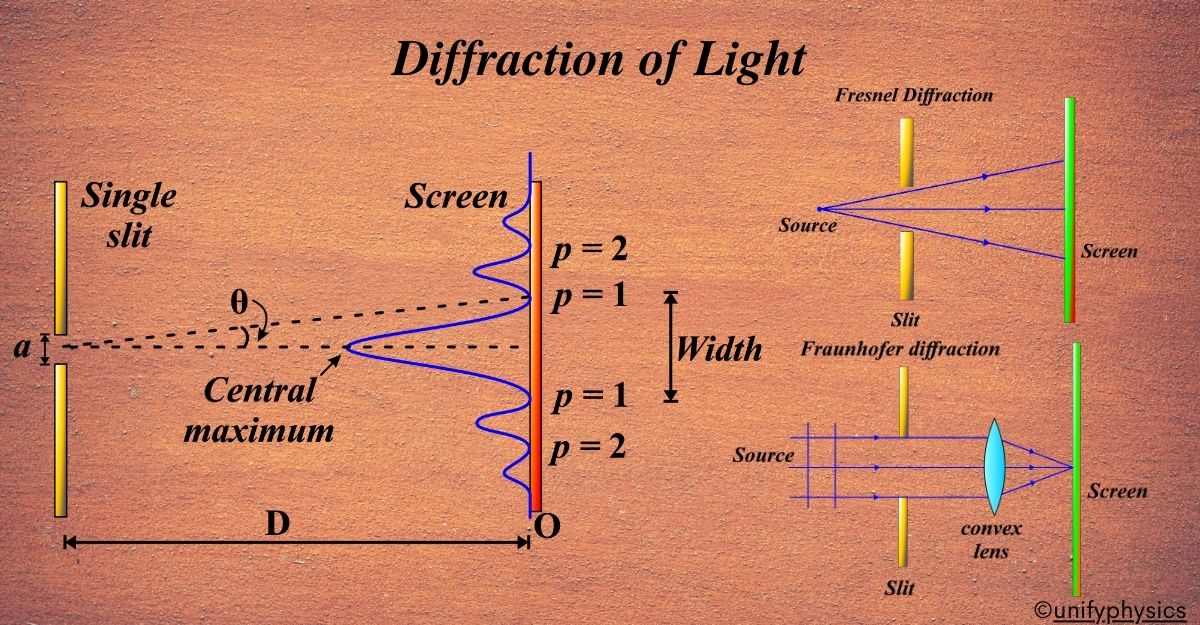
What Is Single Slit Diffraction?

Single Slit Diffraction is a phenomenon that occurs when a wave encounters a slit that is comparable in size to its wavelength. When light passes through a single, narrow slit, it bends and spreads out to form a diffraction pattern characterized by a central bright fringe flanked by several darker and lighter bands.

Imagine you have a narrow slit and a screen behind it. When you shine a light through the slit, instead of just seeing a single bright spot on the screen, you’ll notice a pattern of several bright and dark regions.

This happens because light behaves like a wave. When the light waves pass through the slit, they spread out and overlap with each other, creating an interference pattern. This pattern consists of a central bright region (called the central maximum) and several alternating dark and bright regions on either side.

The central maximum is the result of light from all parts of the slit arriving in phase and adding up constructively at the center of the screen. The dark regions (called minima) occur when the light waves from different parts of the slit arrive out of phase and cancel each other out. The condition for the minima in the diffraction pattern is described by the formula:

\(\displaystyle a \sin(\theta) = m\lambda \)

• ( a ) is the width of the slit,
• ( θ) is the angle relative to the original direction of the light,
• ( m ) is the order of the minimum (an integer),
• (λ) is the wavelength of the light.

This formula helps predict where the dark fringes will appear on the screen. Single Slit Diffraction is a clear demonstration of the wave nature of light. It shows us that light can spread out and interfere with itself, creating patterns that we can predict and analyze.

The Central Maximum:

In single-slit diffraction, The Central Maximum is the brightest spot on the screen and occurs directly in line with the light source. It’s the result of constructive interference where all the light waves passing through different parts of the slit arrive at the center of the screen in phase.

To derive the expression for the central maximum, we’ll start with the basic setup where light of wavelength (λ) passes through a slit of width (a) and forms a diffraction pattern on a screen at a distance (D) from the slit.

The position of the first minima on either side of the central maximum can be found using the condition for destructive interference:

\(\displaystyle a \sin(\theta) = m\lambda \)

where ( m ) is the order of the minima (for the first minima, (\(\displaystyle m = \pm 1 \)) and (θ) is the angle of diffraction.

For small angles, sin(θ) is approximately equal to (θ) in radians. Therefore, the position (y) of the first minima from the center of the screen can be given as:

\(\displaystyle y = D \theta \)

The width of the central maximum, (β), is simply twice the distance from the center to the first minima:

\(\displaystyle \beta = 2y = 2D \theta \)

Substituting (θ) from the minima condition, we get:

\(\displaystyle \beta = 2D \left( \frac{\lambda}{a} \right) \)

Therefore, the width of the central maximum is:

\(\displaystyle\beta = \frac{2\lambda D}{a} \)

The angular width of the central maximum, (2θ), can also be expressed as:

\(\displaystyle 2\theta = \frac{2\lambda}{a} \)

The width of the central maximum is directly proportional to the wavelength of the light and the distance from the slit to the screen, and inversely proportional to the width of the slit. This expression helps us predict how the diffraction pattern will look based on the physical parameters of the setup.

Fraunhofer Diffraction at a Double Slit

Fraunhofer Diffraction at a Double Slit shows us that light behaves like a wave, and when it passes through two slits, it creates an interference pattern of bright and dark bands due to the waves adding up or canceling each other out. This is similar to single-slit diffraction but with two slits, resulting in a more complex pattern of interference and diffraction.

Fraunhofer diffraction at a double slit is a classic physics experiment that demonstrates the wave nature of light. It’s named after Joseph von Fraunhofer, who studied the patterns created when light passes through two closely spaced slits. Imagine you have two very narrow, parallel slits in an opaque material. When a beam of monochromatic (single-color) light shines through these slits, it doesn’t just create two bright lines on a screen behind the slits. Instead, you see a series of bright and dark bands.

This pattern is created because light waves from each slit interfere with each other. Where the peaks of the waves from both slits meet, they add up to make a brighter light (constructive interference). Where a peak from one slit meets a trough from the other, they cancel each other out, creating a dark spot (destructive interference).

The condition for bright fringes (where the light is most intense) in the double-slit experiment is given by:

\(\displaystyle d \sin(\theta) = m\lambda \)

• ( d ) is the distance between the two slits,
• ( θ ) is the angle at which the bright fringe is observed,
• ( m ) is the order of the maximum (an integer),
• ( λ) is the wavelength of the light.

For dark fringes (where the light cancels out), the condition is:

\(\displaystyle d \sin(\theta) = (m + \frac{1}{2})\lambda \)

The result is a series of alternating bright and dark bands known as an interference pattern. The central band is the brightest because it’s where the light from both slits travels the same distance to the screen, meaning all the waves are in step.

Diffraction Grating

A diffraction grating is a powerful tool in optics that separates light into its different wavelengths, revealing the spectrum of colors that make up the light. It’s a clear demonstration of the wave nature of light and the phenomenon of interference. A diffraction grating consists of many equally spaced slits that diffract light to produce multiple beams that interfere and create a spectrum. A diffraction grating is an optical device that consists of a large number of equally spaced parallel slits or grooves. It’s used to disperse light into its component colors or wavelengths.

When light shines on a diffraction grating, it’s split into several beams traveling in different directions. The light waves that emerge from the slits interfere with each other, creating a spectrum of light. The principle behind a diffraction grating is similar to that of double-slit diffraction, but with many more slits, the pattern becomes much more detailed. Each slit acts as a source of light waves, and these waves overlap and interfere to form a complex pattern of bright and dark areas.

The condition for the maxima (bright fringes) in a diffraction grating is given by:

\(\displaystyle d \sin(\theta) = m\lambda \)

The pattern consists of several orders of spectra, with the zeroth order being the central bright spot, and the first, second, third (and so on) orders being the spectra on either side. Diffraction gratings are widely used in spectroscopy, which is the study of the interaction between matter and electromagnetic radiation. They allow scientists to analyze the spectral composition of light sources.

Width of the Maxima:

The width of the maxima in a diffraction grating pattern tells us how spread out the bright fringes are. It’s a direct result of the interference of light waves coming through multiple slits and is a fundamental concept in the study of wave optics. The width of the maxima in a diffraction pattern is inversely proportional to the number of slits in the grating.

When we talk about the width of the maxima in a diffraction grating, we’re referring to how broad the bright fringes (maxima) are in the diffraction pattern. A diffraction grating creates a series of bright and dark bands. The bright bands are where light from the slits adds up constructively, and the dark bands are where it cancels out destructively. The width of these bright bands is an important characteristic of the diffraction pattern.

The width of the maxima is related to the spacing between the slits in the grating and the order of the maxima. It can be determined by measuring the distance between two consecutive minima that flank a maximum and dividing by two.

The angular width of the maxima can be calculated using the formula:

\(\displaystyle \delta \theta = \frac{\lambda}{nd\cos\theta} \)

This formula takes into account the angle (θ) at which the maxima occur, which can affect the spacing between the fringes, especially for higher orders of diffraction where (θ) is larger.

Or

\(\displaystyle \Delta \theta = \frac{\lambda}{nd} \)

• ( \(\displaystyle\Delta \theta\) ) is the angular width of the maxima,
• (λ) is the wavelength of the light,
• ( n ) is the order of the maximum,
• ( d ) is the distance between adjacent slits in the grating.

To find the physical width of the maxima on a screen at a distance ( L ) from the grating, you would use the small angle approximation:

\(\displaystyle \Delta y = L \Delta \theta \)

where (∆y ) is the physical width of the maxima.

The width of the maxima is inversely proportional to the number of slits illuminated. Higher order maxima (larger values of ( n )) are broader than lower order maxima.

Resolving Power

Resolving Power is a measure of the ability of an optical instrument, like a microscope or a camera, to distinguish between two points that are close together. It’s essentially how well the instrument can separate two objects that are very close in distance.

Resolving power determines the clarity of the image produced by an instrument. Higher resolving power means a clearer, more detailed image. It’s limited by the wavelength of light used and the instrument’s design, particularly the size of its aperture or lens.

Shorter wavelengths can resolve finer details because they can distinguish between points that are closer together. Larger apertures allow more light to enter, which can improve the resolution by reducing the effects of diffraction.

Resolving the Power of a Telescope:

The resolving power of a telescope is its ability to distinguish between two closely spaced objects and see them as separate entities. It’s a measure of the detail the telescope can reveal. When astronomers look at stars, planets, or distant galaxies, they want to see as much detail as possible. If a telescope’s resolving power is too low, two stars that are close together might look like a single blurry spot of light. A telescope with high resolving power can show them as two distinct points.

Diffraction is the bending of light around the edges of an obstacle, like a telescope’s aperture, which can cause images to blur. The aperture of a telescope acts as a barrier with a hole (the lens or mirror), and as light passes through this hole, it diffracts, creating a pattern that can limit how well the telescope can resolve details.

The resolving power of a telescope is often given by the formula:

\(\displaystyle R = \frac{1.22 \lambda}{D} \)

The formula tells us that the resolving power is inversely proportional to the diameter of the aperture. This means that larger telescopes (with larger apertures) have better-resolving power because they can collect more light and produce sharper images.

The factor of 1.22 in the formula comes from Rayleigh’s criterion, which is a standard for deciding when two points are resolvable. According to this criterion, two points are considered resolvable when the central maximum of the diffraction pattern of one image falls on the first minimum of the other. The resolving power of a telescope is a crucial aspect that determines the quality of the images it can produce. It’s all about the telescope’s ability to reveal fine details and separate closely spaced celestial bodies in the night sky.

Resolving Power of a Diffraction Grating:

The resolving power of a diffraction grating is its ability to distinguish between two closely spaced wavelengths of light. It’s a measure of how well the grating can separate adjacent spectral lines in a spectrum.

A diffraction grating consists of many closely spaced slits. When light passes through these slits, it diffracts and creates a pattern of interference that results in a spectrum. The quality of this spectrum depends on how well the grating can separate different wavelengths.

The resolving power (R) of a diffraction grating is given by the formula:

\(\displaystyle R = nN \)

• ( n ) is the order of the spectrum (the number of wavelengths by which paths differ),
• ( N ) is the total number of lines on the grating that are illuminated.

The formula tells us that the resolving power increases with the order of the spectrum and the number of lines on the grating. A higher-order means that the path difference between adjacent slits is multiple wavelengths, which enhances the separation of different wavelengths. More lines mean more points of interference, which also improves resolution.

In practice, this means that a grating with more lines per millimeter will have a higher resolving power. This is because there are more opportunities for the light waves to interfere and create a detailed spectrum.

The resolving power is crucial for applications like spectroscopy, where scientists need to analyze the composition of light from sources such as stars or chemical reactions. A higher resolving power allows for a more detailed analysis of the light’s spectrum, revealing more information about the source.

The resolving power of a diffraction grating is an important concept in physics that describes the grating’s ability to separate close wavelengths of light and produce a detailed spectrum. It’s a key factor in the effectiveness of various optical instruments used in scientific research.

Rayleigh’s Criterion

This criterion states that two sources are just resolvable when the principal maximum of one image coincides with the first minimum of the other. Rayleigh’s Criterion is a rule used to determine the resolving power of optical instruments, like microscopes and telescopes. It helps us understand when two light sources are distinct enough to be seen as separate.

Imagine you’re trying to spot two stars in the night sky with a telescope. According to Rayleigh’s Criterion, these stars are considered to be just resolved if the central maximum of the diffraction pattern from one star falls on the first minimum of the diffraction pattern from the other star.

This criterion is crucial because it gives us a quantitative way to measure the ability of an optical instrument to distinguish between two points. The better the resolution, the clearer and more detailed the images we can see.

The criterion can be expressed mathematically as:

\(\displaystyle \theta = 1.22 \frac{\lambda}{D} \)

The formula tells us that the resolving power depends on the wavelength of light and the size of the aperture. A larger aperture or a shorter wavelength will result in a smaller value of ( \theta ), meaning better resolution.

Rayleigh’s Criterion is fundamental in the design and use of optical instruments. It sets the limit for the smallest detail that can be resolved and is used to compare the performance of different devices.

What Is the Difference Between Diffraction and Scattering?

While both involve the spreading of light, diffraction is a specific type of scattering that occurs when light waves encounter obstacles or apertures that are about the same size as their wavelength.

Aspect	Diffraction	Scattering
Definition	Diffraction is the bending of waves around the edges of an obstacle or aperture that is comparable in size to the wavelength of the waves.	Scattering is a broader term that refers to the redirection of light in various directions when it encounters particles or irregularities.
Cause	Caused by the wave nature of light interacting with objects that have dimensions similar to the wavelength of light.	Caused by the interaction of light with particles or imperfections, which can be much smaller, larger, or similar in size to the wavelength of light.
Resulting Pattern	Produces a predictable pattern of bright and dark fringes due to interference.	Results in light being redirected in many directions, often producing no discernible pattern.
Dependency	Highly dependent on the wavelength of light and the size of the aperture or obstacle.	Depends on the size, shape, and material of the particles and the wavelength of light.
Examples	The pattern seen when light passes through a single slit or a diffraction grating.	The blue color of the sky due to the scattering of sunlight by molecules in the atmosphere.

This table outlines the key differences between diffraction and scattering, two phenomena that describe how light interacts with matter. Understanding these differences is important for explaining various optical effects and behaviors of light.

Also Read: Young’s Double Slit Experiment

Examples of Diffraction

Common examples include the pattern seen when light passes through a feather, the colorful effects on a CD, and the bending of light waves around the edges of a door.

• CDs and DVDs: The colorful patterns you see when you hold a CD or DVD up to the light are due to diffraction. The closely spaced tracks on the disc act like a diffraction grating, spreading out the light into its component colors.
• Rainbows: A rainbow is a natural example of diffraction. Water droplets in the atmosphere act like tiny prisms, bending and spreading out sunlight into a spectrum of colors.
• Eyeglasses: The anti-reflective coating on some eyeglasses works by causing destructive interference through diffraction, reducing glare and making it easier to see.
• Holograms: Holograms on credit cards or product packaging are created using diffraction. They record and reconstruct the light field that was originally reflected from an object, creating a three-dimensional image.
• Feathers: The iridescent colors of peacock feathers or butterfly wings are due to microscopic structures that diffract light, creating vivid colors that change with the angle of view.
• Shadow Edges: If you look closely at the edge of a shadow, especially a sharp one cast by a thin object, you might notice a series of dark and light bands. This is due to the diffraction of light around the object’s edges.
• Wire Mesh: Looking through a fine wire mesh or a fabric with a tight weave can produce a diffraction pattern, as the gaps between the wires or threads act like multiple slits.
• Sound Waves: Diffraction isn’t limited to light; it happens with all waves. You can hear sound diffract around corners or through doorways, which is why you can hear someone speaking even if they’re not in direct line of sight.

These examples help tangibly illustrate the concept of diffraction, showing how widespread this phenomenon is in both natural and man-made environments.

Solved Examples

Example 1: Calculate the angular position of the first minimum for a single slit diffraction pattern given that the slit width is ( a = 0.5 mm) and the light used has a wavelength ( λ = 600 nm).

Solution: The condition for the first minimum in a single slit diffraction pattern is given by:

\(\displaystyle a \sin \theta = \lambda\)

Substitute the given values:

\(\displaystyle 0.5 \times 10^{-3} \sin \theta = 600 \times 10^{-9}\)

\(\displaystyle\sin \theta = \frac{600 \times 10^{-9}}{0.5 \times 10^{-3}} = 1.2 \times 10^{-3}\)

Since (θ) is small, (\(\displaystyle \sin \theta \approx \theta\) ) in radians:

\(\displaystyle\theta \approx 1.2 \times 10^{-3} \, \text{radians} = 1.2 \times 10^{-3} \times \frac{180}{\pi} \approx 0.0688^\circ\)

The angular position of the first minimum for the single slit diffraction pattern is approximately ( 0.0688^∘).

Example 2: A circular aperture of diameter 2 mm is illuminated by monochromatic light of wavelength 500 nm. Calculate the radius of the central bright spot (Airy disk) on a screen 1 m away.

Solution: The radius of the Airy disk (central bright spot) in Fresnel diffraction is given by:

\(\displaystyle r = 1.22 \frac{\lambda D}{d}\)

where ( D ) is the distance to the screen, ( d ) is the diameter of the aperture, and (λ) is the wavelength.

Substitute the given values:

\(\displaystyle r = 1.22 \frac{500 \times 10^{-9} \times 1}{2 \times 10^{-3}} = 1.22 \times 0.25 \times 10^{-3} \)

\(\displaystyle = 0.305 \times 10^{-3} \, \text{m} = 0.305 \, \text{mm}\)

The radius of the central bright spot (Airy disk) is 0.305 mm.

Example 3: In a Fraunhofer double slit experiment, the slit separation is ( d = 0.1 mm), and the slit width is ( a = 0.02 mm). If the wavelength of light used is 600 nm, calculate the angular position of the first principal maximum.

Solution: For Fraunhofer diffraction at a double slit, the condition for principal maxima is given by:

\(\displaystyle d \sin \theta = m \lambda\)

where ( m ) is the order of the maximum. For the first principal maximum (m = 1):

\(\displaystyle 0.1 \times 10^{-3} \sin \theta = 600 \times 10^{-9}\)

\(\displaystyle\sin \theta = \frac{600 \times 10^{-9}}{0.1 \times 10^{-3}} = 6 \times 10^{-3}\)

Since (θ) is small:

\(\displaystyle\theta \approx 6 \times 10^{-3} \, \text{radians} = 6 \times 10^{-3} \times \frac{180}{\pi} \approx 0.343^\circ\)

The angular position of the first principal maximum is approximately ( 0.343^∘).

Example 4: A diffraction grating has 5000 lines per cm. Calculate the angle of diffraction for the second-order maximum for light of wavelength 450 nm.

Solution: The grating equation is given by:

\(\displaystyle d \sin \theta = m \lambda\)

where ( d ) is the grating spacing, ( m ) is the order, and (λ) is the wavelength. The grating spacing ( d ) can be calculated as:

\(\displaystyle d = \frac{1}{5000 \, \text{lines/cm}} = \frac{1}{5000 \times 10^2 \, \text{lines/m}} = 2 \times 10^{-6} \, \text{m}\)

For the second-order maximum (m = 2 ):

\(\displaystyle 2 \times 10^{-6} \sin \theta = 2 \times 450 \times 10^{-9}\)

\(\displaystyle\sin \theta = \frac{900 \times 10^{-9}}{2 \times 10^{-6}} = 0.45\)

\(\displaystyle\theta = \sin^{-1}(0.45) \approx 26.74^\circ\)

The angle of diffraction for the second-order maximum is approximately ( 26.74^∘).

Example 5: Calculate the resolving power of a telescope with an objective lens diameter of 1.2 m using light of wavelength 550 nm.

Solution: The resolving power ( R ) is given by Rayleigh’s criterion:

\(\displaystyle R = \frac{1.22 \lambda}{D}\)

Substitute the given values:

[
\(\displaystyle R = \frac{1.22 \times 550 \times 10^{-9}}{1.2} = \frac{671 \times 10^{-9}}{1.2} \)

\(\displaystyle = 559.2 \times 10^{-9} \, \text{radians}\)

Convert to arcseconds (1 radian = ( 206265 ) arcseconds):

\(\displaystyle R = 559.2 \times 10^{-9} \times 206265 \approx 0.115 \, \text{arcseconds}\)

The resolving power of the telescope is approximately ( 0.115 ) arcseconds.

Example 6: Two stars are observed with a telescope with an objective lens diameter of 0.5 m. If the wavelength of light used is 600 nm, calculate the minimum angular separation that can be resolved using Rayleigh’s criterion.

Solution: Rayleigh’s criterion for the minimum angular separation (θ) is given by:

\(\displaystyle\theta = 1.22 \frac{\lambda}{D}\)

Substitute the given values:

\(\displaystyle\theta = 1.22 \frac{600 \times 10^{-9}}{0.5} = 1.22 \times 1.2 \times 10^{-6} \)

\(\displaystyle = 1.464 \times 10^{-6} \, \text{radians}\)

Convert to arcseconds:

\(\displaystyle\theta = 1.464 \times 10^{-6} \times 206265 \approx 0.302 \, \text{arcseconds}\)

The minimum angular separation that can be resolved is approximately ( 0.302 ) arcseconds.

FAQs